Colabore! Saiba mais screen_rotation

Ao navegar por este site , você concorda com a Política de Uso de Dados.

| | | | |

2 Equação com Uma Incógnita 2 Equação com Uma Incógnita 2.2 Método da Falsa Posição

2.1 Método da Bisseção

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

O método da bisseção explora o fato de que toda função contínua $f$ com $f(a)\cdot f(b)<0$ (i.e., $f(a)$ e $f(b)$ tem sinais diferentes) tem pelo menos um zero no intervalo $(a,b)$ ⁹⁹endnote: ⁹Esta é uma consequência imediata do Teorema do Valor Intermediário..

Exemplo 2.1.1.

Consideramos o problema de resolver a equação

	$\displaystyle\operatorname{sen}^{2}\left(x+\frac{\pi}{4}\right)$	$\displaystyle=x^{3}-\frac{\pi}{4}x^{2}$		(2.2)
		$\displaystyle-\frac{5\pi^{2}}{16}x-\frac{3\pi^{3}}{64}.$		(2.2)

Este problema é equivalente a encontrar os zeros da seguinte função

	$\displaystyle f(x)$	$\displaystyle=\operatorname{sen}^{2}\left(x+\frac{\pi}{4}\right)-x^{3}$		(2.3)
		$\displaystyle+\frac{\pi}{4}x^{2}+\frac{5\pi^{2}}{16}x+\frac{3\pi^{3}}{64}.$		(2.3)

Os zeros exatos¹⁰¹⁰endnote: ¹⁰O problema foi construído para que tivesse estas soluções. desta função são $x_{1}=3\pi/4\approx 2.3562$ e $x_{2}=x_{3}=-\pi/4\approx-0.78540$ (consulte a Figura 2.1).

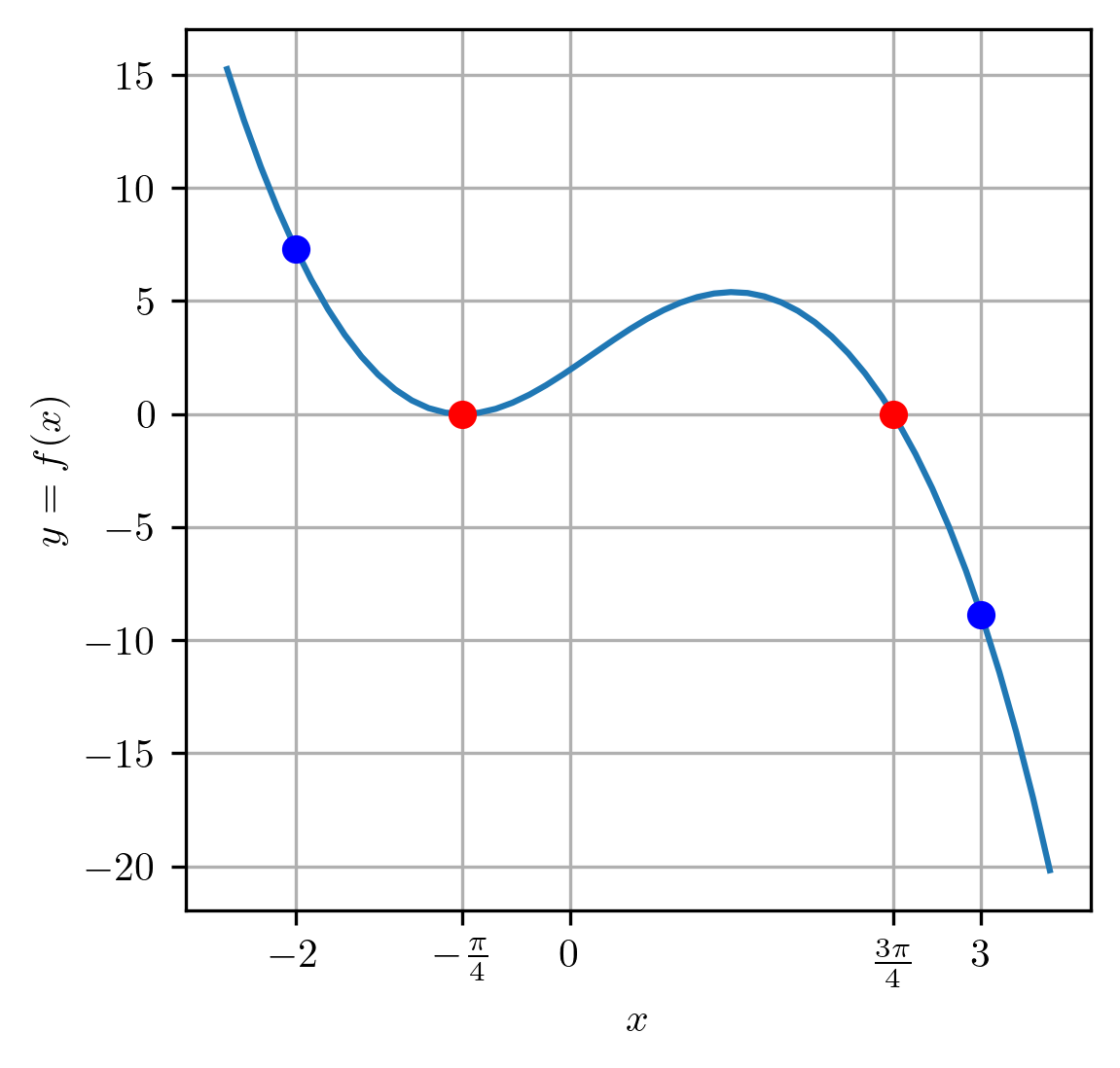
Refer to caption — Figura 2.1: Função $f$ do Exemplo 2.1.1.

Observamos que esta função é contínua e que, por exemplo, $f(-2)>0$ e $f(3)<0$ , logo $f(-2)\cdot f(3)<0$ e, de fato, $f$ tem pelo menos um zero¹¹¹¹endnote: ¹¹De fato, $f$ tem três zeros no intervalo $(-2,3)$ . no intervalo $(-2,3)$ .

Consideramos, então, uma função $f$ contínua tal que $f(a)\cdot f(b)<0$ . O método da bisseção é iterativo, a primeira aproximação para uma solução de $f(x)=0$ é tomada como o ponto médio do intervalo $(a,b)$ , i.e.

x^{(0)}=\frac{a^{(1)}+b^{(1)}}{2},

(2.4)

onde $a^{(0)}=a$ e $b^{(0)}=b$ . Daí, se ocorrer $f(x^{(0)})=0$ o problema está resolvido. Caso contrário, $f$ tem pelo menos um zero num dos subintervalos $(a^{(0)},x^{(0)})$ ou $(x^{(0)},b^{(0)})$ , pois $f(a^{(0)})\cdot f(x^{(0)})<0$ ou $f(x^{(0)})\cdot f(b^{(0)})<0$ , respectivamente e exclusivamente. No primeiro caso, escolhemos $(a^{(1)},b^{(1)})=(a^{(0)},x^{(0)})$ ou, no segundo caso, tomamos $(a^{(1)},b^{(1)})=(x^{(0)},b^{(0)})$ . Então, a segunda aproximação para uma solução é computada como

x^{(1)}=\frac{a^{(1)}+b^{(1)}}{2}.

(2.5)

O procedimento se repete até obtermos uma aproximação com a precisão desejada.

Exemplo 2.1.2.

Consideremos o problema de encontrar um zero da função

	$\displaystyle f(x)$	$\displaystyle=\operatorname{sen}^{2}\left(x+\frac{\pi}{4}\right)-x^{3}$		(2.6)
		$\displaystyle+\frac{\pi}{4}x^{2}+\frac{5\pi^{2}}{16}x+\frac{3\pi^{3}}{64}.$		(2.6)

Do esboço de seu gráfico (Figura 2.1), observamos que $f(2)\cdot f(3)\neq 0$ sendo que o zero $x=3\pi/4\approx 2.3562$ de $f$ está no intervalo $(2,3)$ . Aplicando o método da bisseção com intervalo inicial $(a^{(0)},b^{(0)})=(2,3)$ e aproximação inicial $x^{(0)}=(a^{(0)}+b^{(0)})/2$ , obtemos as aproximações apresentadas na Tabela 2.1.

Tabela 2.1: Resultados referentes ao Exemplo 2.1.2.

k	$a^{(k)}$	$b^{(k)}$	$x^{(k)}$	$s$
0	$2.0000$	$3.0000$	$2.5000$	-1
1	$2.0000$	$2.5000$	$2.2500$	1
2	$2.2500$	$2.5000$	$2.3750$	-1
3	$2.2500$	$2.3750$	$2.3125$	1
4	$2.3125$	$2.3750$	$2.3438$	1
5	$2.3438$	$2.3750$	$2.3594$	-1
6	$2.3438$	$2.3594$	$2.3516$	1
7	$2.3516$	$2.3594$	$2.3555$	1
8	$2.3555$	$2.3594$	$2.3574$	-1
9	$2.3555$	$2.3574$	$2.3564$	-1
$s:=f(a^{(k)})\cdot f(x^{(k)})$

⬇

1import numpy as np

3f = lambda x: np.sin(x+np.pi/4)**2 \

4 - x**3 + np.pi/4*x**2 + 5*np.pi**2/16*x \

5 + 3*np.pi**3/64

7a = 2

8b = 3

9x = (a + b)/2

10print(f"0: a={a:.4f}, b={b:.4f}, x={x:.4f}")

11for k in range(9):

12 s = np.sign(f(a)*f(x))

13 if (s == -1):

14 b = x

15 elif (s == 1):

16 a = x

17 else:

18 break

19 x = (a + b)/2

20 print(f"{k+1}: a={a:.4f}, b={b:.4f}, x={x:.4f}")

2.1.1 Análise Numérica

Dada uma função contínua $f:[a,b]\to\mathbb{R}$ com $f(a)\cdot f(b)<0$ , vamos mostrar que o método da bisseção é globalmente convergente e tem ordem de convergência linear.

Definição 2.1.1.

(Método Iterativo Globalmente Convergente.) Um método iterativo

	$\displaystyle x^{(0)}=\text{aprox. inicial},$		(2.7)
	$\displaystyle x^{(k+1)}=g\left(x^{k}\right),$		(2.8)

com $k=0.1,\ldots$ , é dito globalmente convergente, quando

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\lim_{k\to% \infty}\left|x^{(k+1)}-x^{(k)}\right|=0}

(2.9)

para qualquer escolha de $x^{(0)}$ .

Definição 2.1.2.

(Ordem de convergência.) Seja $\left(x^{(k)}\right)_{k=1}^{\infty}$ uma sequência convergente com

\lim_{k\to\infty}\left|x^{(k+1)}-x^{(k)}\right|=0,

(2.10)

com $x^{(k+1)}-x^{(k)}\neq 0$ para todo $k$ . Dizemos que $\left(x^{(k)}\right)_{k=1}^{\infty}$ converge com ordem $\alpha>0$ e com constante de erro assintótica $C>0$ , quando

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\lim_{k\to% \infty}\frac{\left|x^{(k+1)}-x^{*}\right|}{\left|x^{(k)}-x^{*}\right|^{\alpha}% }=C}.

(2.11)

Em geral, quando maior o valor de $\alpha$ , mais rapidamente é a convergência das iteradas de um método iterativo. Os seguintes casos são particularmente importantes:

•

Se $\alpha=1$ e $C<1$ , o método é linearmente convergente.
•

Se $\alpha=2$ , o método é quadraticamente convergente.

Convergência e Precisão

Teorema 2.1.1.

Seja $f:[a,b]\to\mathbb{R}$ função contínua com $f(a)\cdot f(b)<0$ . Então, o método da bisseção é globalmente convergente.

Demonstração.

Seja $(x^{(k)})_{k=1}^{\infty}$ a sequência de aproximações¹²¹²endnote: ¹²Caso, $f\left(a^{(k)}\right)=0$ ou $f\left(a^{(b)}\right)=0$ , então assumimos que $a^{(k+i)}=a^{(k)}$ ou $b^{(k+i)}=b^{(k)}$ , conforme o caso, para $i=1,2,3,\ldots$ . do método da bisseção. Por construção, temos

$\displaystyle\left\|x^{(k)}-x^{(k-1)}\right\|$	$\displaystyle\leq b^{(k-1)}-a^{(k-1)}$	(2.12)
	$\displaystyle\leq\frac{b^{(k-2)}-a^{(k-2)}}{2}$	(2.13)
	$\displaystyle\vdots$	(2.14)
	$\displaystyle\leq\frac{b^{(0)}-a^{(0)}}{2^{k-1}}$	(2.15)

Ou seja, obtemos a estimativa de convergência

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\left|x^{(k)}-% x^{(k-1)}\right|\leq\frac{b^{(0)}-a^{(0)}}{2^{k-1}}}

(2.16)

Daí, segue que

	$\displaystyle\lim_{k\to\infty}\left\|x^{(k)}-x^{(k-1)}\right\|$	$\displaystyle=\lim_{k\to\infty}b^{(k)}-a^{(k-1)}$		(2.17)
		$\displaystyle=0.$		(2.18)

∎

Exemplo 2.1.3.

No Exemplo 2.1.2 aplicamos o método da bisseção para a função

	$\displaystyle f(x)$	$\displaystyle=\operatorname{sen}^{2}\left(x+\frac{\pi}{4}\right)-x^{3}$		(2.19)
		$\displaystyle+\frac{\pi}{4}x^{2}+\frac{5\pi^{2}}{16}x+\frac{3\pi^{3}}{64}.$		(2.19)

no intervalo $(2,3)$ . Ao recuperarmos os valores de $\left|x^{(k)}-x^{(k-1)}\right|$ obtemos

$k$	$x^{(k)}$	$\left\|x^{(k)}-x^{(k-1)}\right\|$
$0$	$2.5000$	-x-
$1$	$2.2500$	$2.5\times 10^{-1}$
$2$	$2.3750$	$1.2\times 10^{-1}$
$3$	$2.3125$	$6.2\times 10^{-2}$
$4$	$2.3438$	$3.1\times 10^{-2}$
$5$	$2.3594$	$1.6\times 10^{-2}$
$6$	$2.3516$	$7.8\times 10^{-3}$
$7$	$2.3555$	$3.9\times 10^{-3}$
$8$	$2.3574$	$2.0\times 10^{-3}$
$9$	$2.3564$	$9.8\times 10^{-4}$

Observamos que os valores estão de acordo com a estimativa de convergência 2.16, donde

	$\displaystyle\|x^{(9)}-x^{(8)}\|$	$\displaystyle\leq\frac{b^{(0)}-a^{(0)}}{2^{9}}$		(2.20)
		$\displaystyle=\frac{3-2}{2^{9}}=1.9\times 10^{-3}$		(2.21)

O Teorema 2.1.1 nos garante a convergência do método da bisseção e uma estimativa de precisão (Equação 2.16). O teorema não garante que o método converge para um zero da função objetivo, apenas garante que as aproximações convergem para algum valor no intervalo inicial dado.

Convergência e Exatidão

Dada uma função contínua e estritamente monótona¹³¹³endnote: ¹³Função estritamente crescente ou estritamente decrescente, exclusivamente. $f:[a,b]\to\mathbb{R}$ com $f(a)\cdot f(b)<0$ , temos que o método da bisseção converge para o zero de $f$ em $[a,b]$ .

Teorema 2.1.2.

Seja $f:[a,b]\to\mathbb{R}$ função contínua e estritamente monótona com $f(a)\cdot f(b)<0$ . Então, o método da bisseção converge para o zero de $f$ em $[a,b]$ .

Demonstração.

Das hipóteses temos que $f$ tem um único zero $x^{*}$ em $(a,b)$ . Seja $(x^{(k)})_{k=1}^{\infty}$ a sequência de aproximações¹⁴¹⁴endnote: ¹⁴Caso, $f\left(a^{(k)}\right)=0$ ou $f\left(a^{(b)}\right)=0$ , então assumimos que $a^{(k+i)}=a^{(k)}$ ou $b^{(k+i)}=b^{(k)}$ , conforme o caso, para $i=1,2,3,\ldots$ . do método da bisseção. Por construção, temos

$\displaystyle\|x^{(k)}-x^{*}\|$	$\displaystyle\leq\frac{b^{(k)}-a^{(k)}}{2}$	(2.22)
	$\displaystyle\leq\frac{b^{(k-1)}-a^{(k-1)}}{2^{2}}$	(2.23)
	$\displaystyle\vdots$	(2.24)
	$\displaystyle\leq\frac{b^{(1)}-a^{(1)}}{2^{k}},$	(2.25)

donde, obtemos a seguinte estimativa do erro de truncamento

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}|x^{(k)}-x^{*}% |\leq\frac{b^{(1)}-a^{(1)}}{2^{k}}}.

(2.26)

E, daí também, segue que o método converge para o zero de $f$ , pois

\lim_{k\to\infty}|x^{(k)}-x^{*}|=\lim_{k\to\infty}\frac{b^{(1)}-a^{(1)}}{2^{k}% }=0.

(2.27)

∎

Observação 2.1.1.

(Estimativa de Exatidão.) A estimativa de truncamento 2.26 é também um estimativa de exatidão, i.e. nos fornece uma medida do erro na $k$ -ésima aproximação do método da bisseção.

Exemplo 2.1.4.

No Exemplo 2.1.2 aplicamos o método da bisseção para a função

	$\displaystyle f(x)$	$\displaystyle=\operatorname{sen}^{2}\left(x+\frac{\pi}{4}\right)-x^{3}$		(2.28)
		$\displaystyle+\frac{\pi}{4}x^{2}+\frac{5\pi^{2}}{16}x+\frac{3\pi^{3}}{64}.$		(2.28)

no intervalo $(2,3)$ . A aplicação do método, nos fornece

$k$	$x^{(k)}$	$\left\|x^{(k)}-x^{*}\right\|$
$0$	$2.3560$	$1.4\times 10^{-1}$
$1$	$2.2500$	$1.1\times 10^{-1}$
$2$	$2.3750$	$1.9\times 10^{-2}$
$3$	$2.3125$	$4.4\times 10^{-2}$
$4$	$2.3438$	$1.2\times 10^{-2}$
$5$	$2.3594$	$3.2\times 10^{-3}$
$6$	$2.3516$	$4.6\times 10^{-3}$
$7$	$2.3555$	$7.3\times 10^{-4}$
$8$	$2.3574$	$1.2\times 10^{-3}$
$9$	$2.3564$	$2.5\times 10^{-4}$

onde, $x^{*}=x_{1}=3\pi/4$ . Observamos que este resultado é consistente com a estimativa do erro de truncamento (2.26), da qual temos

	$\displaystyle\|x^{(9)}-x^{*}\|$	$\displaystyle\leq\frac{b^{(0)}-a^{(0)}}{2^{10}}$		(2.29)
		$\displaystyle=\frac{1}{2^{10}}=1.0\mathrm{e}\!-\!3.$		(2.30)

Observação 2.1.2.

(Ordem de Convergência Linear.) A estimativa de convergência (2.26) também pode ser usada para mostrarmos que, assintoticamente, o método da bisseção tem a seguinte taxa de convergência linear

\left|x^{(k+1)}-x^{(k)}\right|\lesssim\frac{1}{2}\left|x^{(k)}-x^{(k-1)}\right% |^{\boldsymbol{1}}.

(2.31)

2.1.2 Zeros de Multiplicidade Par

Sejam $f$ uma função suave e $x^{*}$ um zero de multiplicidade par de $f$ . Observamos que o método da bisseção não é diretamente aplicável para aproximar $x^{*}$ . Isto ocorre, pois, neste caso, $x^{*}$ será um ponto de mínimo ou de máximo local de $f$ , não havendo pontos $a$ e $b$ próximos de $x^{*}$ tal que $f(a)\cdot f(b)<0$ .

Agora, sendo $x^{*}$ um zero de $f$ de multiplicidade $2m$ , temos que ela admite a seguinte decomposição

f(x)=(x-x^{*})^{2m}g(x),

(2.32)

onde $g$ é uma função suave e $g(x^{*})\neq 0$ . Daí, a derivada de $f$

f^{\prime}(x)=2m(x-x^{*})^{2m-1}g(x)+(x-x^{*})^{2m}g^{\prime}(x),

(2.33)

tem $x^{*}$ como um zero de multiplicidade $2m-1$ (ímpar) e, desta forma, podemos aplicar o método da bisseção em $f^{\prime}$ para aproximar $x^{*}$ .

Exemplo 2.1.5.

A função

	$\displaystyle f(x)$	$\displaystyle=\operatorname{sen}^{2}\left(x+\frac{\pi}{4}\right)-x^{3}$		(2.34)
		$\displaystyle+\frac{\pi}{4}x^{2}+\frac{5\pi^{2}}{16}x+\frac{3\pi^{3}}{64}.$		(2.34)

tem $x=-\pi/4\approx-0.7854$ como um zero de multiplicidade par (veja Figura 2.2).

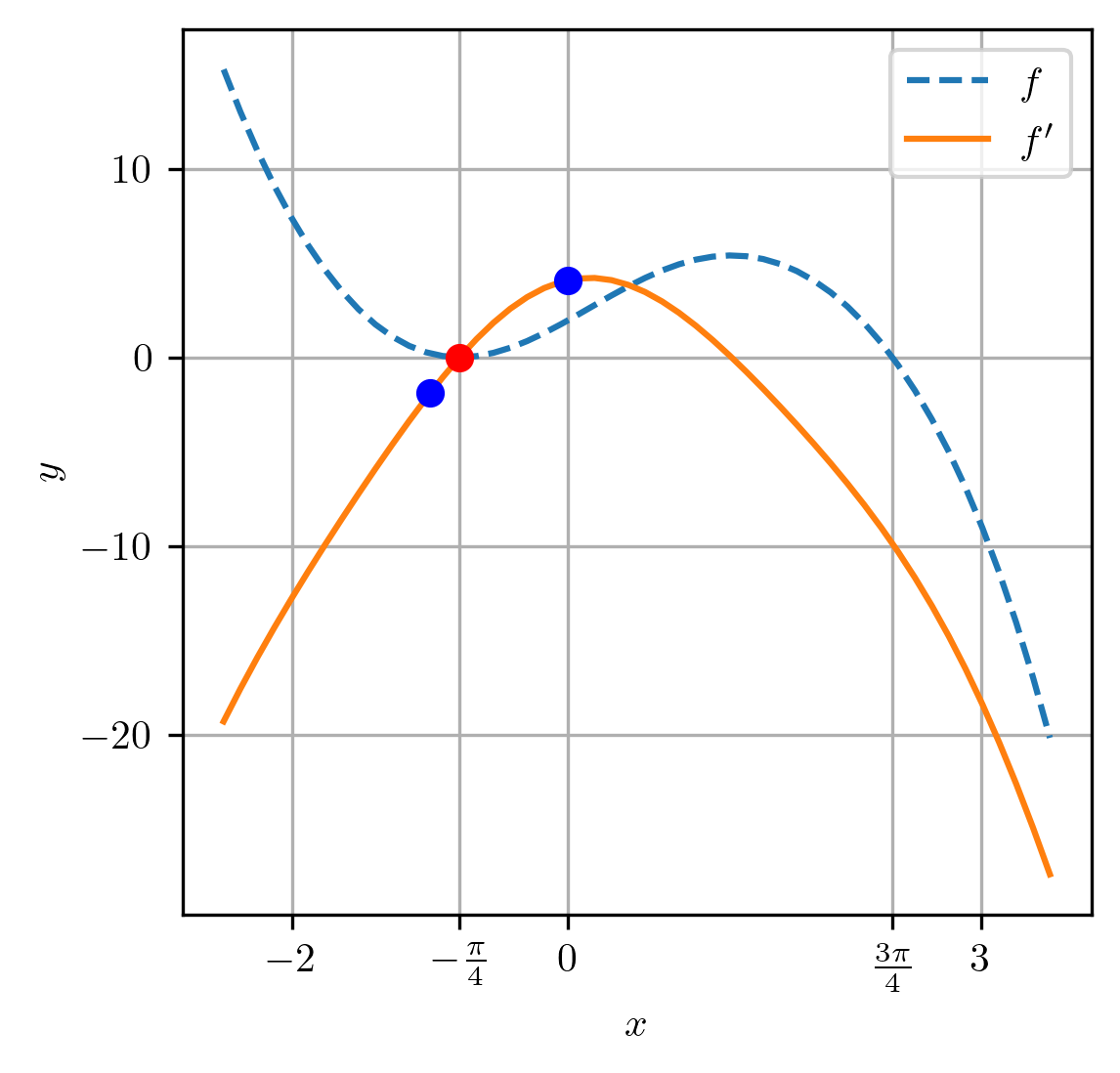
Para aplicarmos o método da bisseção para aproximarmos este zero, primeiramente, derivamos $f$

	$\displaystyle f^{\prime}(x)$	$\displaystyle=2\sin(x+\pi/4)\cos(x+\pi/4)-3x^{2}$		(2.35)
		$\displaystyle+\frac{\pi}{2}x+\frac{5\pi^{2}}{16}.$		(2.35)

O esboço do gráfico de $f^{\prime}$ (Figura 2.2) mostra que $f^{\prime}(-1)\cdot f^{\prime}(0)<0$ sendo que no intervalo $(-1,0)$ $f^{\prime}$ tem um zero de multiplicidade ímpar. Então, aplicando o método da bisseção a $f^{\prime}$ no intervalo inicial $(a^{(1)},b^{(1)})=(-1,0)$ , obtemos os resultados apresentados na Tabela 2.2. Nesta tabela são apresentados as iteradas até a convergência da solução com precisão de $10^{-3}$ .

Tabela 2.2: Resultados referentes ao Exemplo 2.1.2.

$s:=f^{\prime}(a^{(k)})\cdot f^{\prime}(x^{(k)})$
k	$a^{(k)}$	$b^{(k)}$	$x^{(k)}$	$s$
0	$-1.0000\mathrm{e}\!+\!0$	$0.0000\mathrm{e}\!+\!0$	$-5.0000\mathrm{e}\!-\!1$	-1
1	$-1.0000\mathrm{e}\!+\!0$	$-5.0000\mathrm{e}\!-\!1$	$-7.5000\mathrm{e}\!-\!1$	-1
2	$-1.0000\mathrm{e}\!+\!0$	$-7.5000\mathrm{e}\!-\!1$	$-8.7500\mathrm{e}\!-\!1$	1
3	$-8.7500\mathrm{e}\!-\!1$	$-7.5000\mathrm{e}\!-\!1$	$-8.1250\mathrm{e}\!-\!1$	1
4	$-8.1250\mathrm{e}\!-\!1$	$-7.5000\mathrm{e}\!-\!1$	$-7.8125\mathrm{e}\!-\!1$	-1
5	$-8.1250\mathrm{e}\!-\!1$	$-7.8125\mathrm{e}\!-\!1$	$-7.9688\mathrm{e}\!-\!1$	1
6	$-7.9688\mathrm{e}\!-\!1$	$-7.8125\mathrm{e}\!-\!1$	$-7.8906\mathrm{e}\!-\!1$	1
7	$-7.8906\mathrm{e}\!-\!1$	$-7.8125\mathrm{e}\!-\!1$	$-7.8516\mathrm{e}\!-\!1$	-1
8	$-7.8906\mathrm{e}\!-\!1$	$-7.8516\mathrm{e}\!-\!1$	$-7.8711\mathrm{e}\!-\!1$	1
9	$-7.8711\mathrm{e}\!-\!1$	$-7.8516\mathrm{e}\!-\!1$	$-7.8613\mathrm{e}\!-\!1$	1

2.1.3 Exercícios

E. 2.1.1.

Use o método da bisseção para aproximar um zero de

f(x)=x^{3}\operatorname{sen}(x)-\cos(x)

(2.36)

aplicando como intervalo inicial $(a^{(0)},b^{(0)})=(0.5,1)$ e aproximação inicial $x^{(0)}=(a^{(0)}+b^{(0)})/2$ . Faça, então, $6$ iterações de forma a obter a aproximação $x^{(6)}$ e forneça-a com $7$ dígitos significativos por arredondamento.

Resposta.

$9.179688\times 10^{-1}$

E. 2.1.2.

Considere o método da bisseção para aproximar um zero de $f(x)=x^{3}\operatorname{sen}(x)-\cos(x)$ , aplicando como intervalo inicial $(a^{(0)},b^{(0)})=(0.5,1)$ e aproximação inicial $x^{(0)}=(a^{(0)}+b^{(0)})/2$ . Use a estimativa de convergência (2.26)

\left|x^{(k)}-x^{*}\right|\leq\frac{b^{(0)}-a^{(0)}}{2^{k}},

(2.37)

para estimar o número mínimo de iterações $k_{conv}$ necessárias para se obter a solução com exatidão de $10^{-4}$ . Então, compute $x^{(k_{conv})}$ e forneça-o com $6$ dígitos significativos por arredondamento.

Resposta.

$9.15833\mathrm{e}\!-\!1$

E. 2.1.3.

Use o método da bisseção para computar a(s) solução(ões) das seguintes equações com precisão de 8 dígitos significativos.

a)

$x=2^{-x}$ para $0\leq x\leq 2$ .
b)

$e^{-x^{2}}=3x-x^{2}$ para $-1\leq x\leq 4$ .

Resposta.

a) $6.4118574\times 10^{-1}$ ; b) $3.3536470\times 10^{-1}$ ; $2.9999589$

E. 2.1.4.

Use o método da bisseção para encontrar uma aproximação com precisão de $10^{-4}$ do zero de

	$\displaystyle f(x)$	$\displaystyle=(-x^{2}+1.154x-0.332929)\cos(x)+x^{2}$
		$\displaystyle-1.154x+0.332929$		(2.38)

no intervalo $(0.55,0.65)$ . Forneça a aproximação computada com $7$ dígitos significativos por arredondamento.

Resposta.

$5.770508\times 10^{-1}$

E. 2.1.5.

Aplique o método da bisseção para encontrar o ponto crítico¹⁵¹⁵endnote: ¹⁵Definimos que $x$ é ponto crítico de uma dada $f$ , quando $f^{\prime}(x)=0$ ou $\nexists f^{\prime}(x)$ . de

f(x)=(1-x^{2})e^{-x^{2}}

(2.39)

no intervalo $(0,2)$ . Obtenha o resultado com precisão de $5$ dígitos significativos por arredondamento.

Resposta.

$1.4142\mathrm{e}\!+\!0$

Envie seu comentário

As informações preenchidas são enviadas por e-mail para o desenvolvedor do site e tratadas de forma privada. Consulte a Política de Uso de Dados para mais informações. Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

| | | |