Colabore! Saiba mais screen_rotation

Ao navegar por este site , você concorda com a Política de Uso de Dados.

| | | | |

6 Aproximação por Mínimos Quadrados 6 Aproximação por Mínimos Quadrados 6.2 Problemas Não Lineares

6.1 Problemas Lineares

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

Dado um conjunto de $n$ pontos $\{(x_{i},y_{i})\}_{i=1}^{n}$ , $x_{i}\neq x_{j}$ para $i\neq j$ , e uma família de $m\leq n$ funções $\{f_{i}(x)\}_{i=1}^{m}$ , o problema linear de aproximação por mínimos quadrados consiste em determinar os $m$ coeficientes $\{c_{i}\}_{i=1}^{m}$ tal que a função

	$\displaystyle\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}f(x;% \boldsymbol{c})=\sum_{j=1}^{m}c_{j}f_{j}(x)$		(6.1)
	$\displaystyle\text{}\qquad=c_{1}f_{1}(x)+c_{2}f_{2}(x)+c_{3}f_{3}(x)+\cdots+c_% {m}f_{m}(x)$		(6.2)

aproxime o dado conjunto de pontos no sentido de mínimos quadrados, i.e. o vetor dos coeficientes $\boldsymbol{c}=(c_{1},c_{2},\dotsc,c_{m})$ é solução do seguinte problema linear de minimização

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\min_{% \boldsymbol{c}}\left\{E:=\sum_{i=1}^{n}\left|y_{i}-f(x_{i};\boldsymbol{c})% \right|^{2}\right\}.

(6.3)

A fim de trabalharmos com uma notação mais compacta, definimos o resíduo $\boldsymbol{r}(\boldsymbol{c})=(r_{1}(\boldsymbol{c}),r_{2}(\boldsymbol{c}),% \dotsc,r_{n}(\boldsymbol{c}))$ , onde $\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}r_{i}(% \boldsymbol{c}):=y_{i}-f(x_{i};\boldsymbol{c})$ . Com esta notação, o problema de mínimos quadrados se resume a resolver

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\min_{\textbf{% c}}\{E:=\left\|r(\boldsymbol{c})\right\|^{2}\}.

(6.4)

6.1.1 Método das Equações Normais

A fim de resolver o problema de mínimos quadrados (6.4), observamos que o erro quadrático

	$\displaystyle E:=\left\\|\boldsymbol{r}(\boldsymbol{c})\right\\|_{2}^{2}=\sum_{i% =1}^{n}r_{i}^{2}(\boldsymbol{c})$		(6.5)
	$\displaystyle\text{}\quad=\sum_{i=1}^{n}\left(y_{i}-f(x_{i};\boldsymbol{c})% \right)^{2}$		(6.6)
	$\displaystyle\text{}\quad=\sum_{i=1}^{n}\left(y_{i}-\sum_{j=1}^{m}c_{j}f_{j}(x% _{i})\right)^{2}$		(6.7)
	$\displaystyle\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}E=\\|% \boldsymbol{y}-A\boldsymbol{c}\\|^{2},$		(6.8)

onde $\boldsymbol{y}:=(y_{1},y_{2},\dotsc,y_{n})$ e

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}A:=\begin{% bmatrix}f_{1}(x_{1})&f_{2}(x_{1})&\cdots&f_{m}(x_{1})\\ f_{1}(x_{2})&f_{2}(x_{2})&\cdots&f_{m}(x_{2})\\ \vdots&\vdots&\vdots&\vdots\\ f_{1}(x_{n})&f_{2}(x_{n})&\cdots&f_{m}(x_{n})\end{bmatrix}.

(6.9)

Os parâmetros $c_{j}$ que minimizam o erro $E$ são solução do seguinte sistema de equações

\frac{\partial E}{\partial c_{j}}=2\sum_{i=0}^{n}r_{i}(c)\frac{\partial}{% \partial c_{j}}r_{i}(c)=0,

(6.10)

onde $j=1,2,\dotsc,m$ . Ou, em uma notação mais apropriada,

	$\displaystyle\nabla_{\boldsymbol{c}}E=0$		(6.11)
	$\displaystyle-A^{T}\boldsymbol{r}(\boldsymbol{c})=0$		(6.12)
	$\displaystyle-A^{T}(\boldsymbol{y}-A\boldsymbol{c})=0$		(6.13)
	$\displaystyle A^{T}A\boldsymbol{c}=A^{T}\boldsymbol{y}.$		(6.14)

Portanto, o problema linear de mínimos quadrados se resume em resolver as chamadas equações normais

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}A^{T}A% \boldsymbol{c}=A^{T}\boldsymbol{y}.

(6.15)

Concluímos que a solução é dada por

\boldsymbol{c}=\left(A^{T}A\right)^{-1}A^{T}\boldsymbol{y},

(6.16)

quando $A^{T}A$ é inversível.

Exemplo 6.1.1 (Ajuste de Polinômios).

Considere o problema de ajustar o conjunto de pontos

$i$	$x_{i}$	$y_{i}$
$1$	$-1.0$	$1.2$
$2$	$0.0$	$-0.1$
$3$	$1.0$	$0.7$
$4$	$1.5$	$2.4$

por um polinômio quadrático

p(x)=p_{1}x^{2}+p_{2}x+p_{3}

(6.17)

no sentido de mínimos quadrados.

Refer to caption — Figura 6.1: Polinômio ajustado no Exemplo 6.1.1.

Neste caso, a família de funções do problema de mínimos quadrados é $f_{1}(x)=x^{2}$ , $f_{2}(x)=x$ e $f_{3}(x)=1$ . Assim sendo, os coeficientes $p=(p_{1},p_{2},p_{3})$ são solução do seguinte sistema linear

A^{T}A\boldsymbol{p}=A^{T}\boldsymbol{y},

(6.18)

onde $\boldsymbol{y}=(y_{1},y_{2},y_{3})$ e

A:=\begin{bmatrix}x_{1}^{2}&x_{1}&1\\ x_{2}^{2}&x_{2}&1\\ x_{3}^{2}&x_{3}&1\\ x_{4}^{2}&x_{4}&1\end{bmatrix}.

(6.19)

Emfim, resolvendo as equações normais (6.18), obtemos

p(x)=1.25x^{2}-0.188x-0.203.

(6.20)

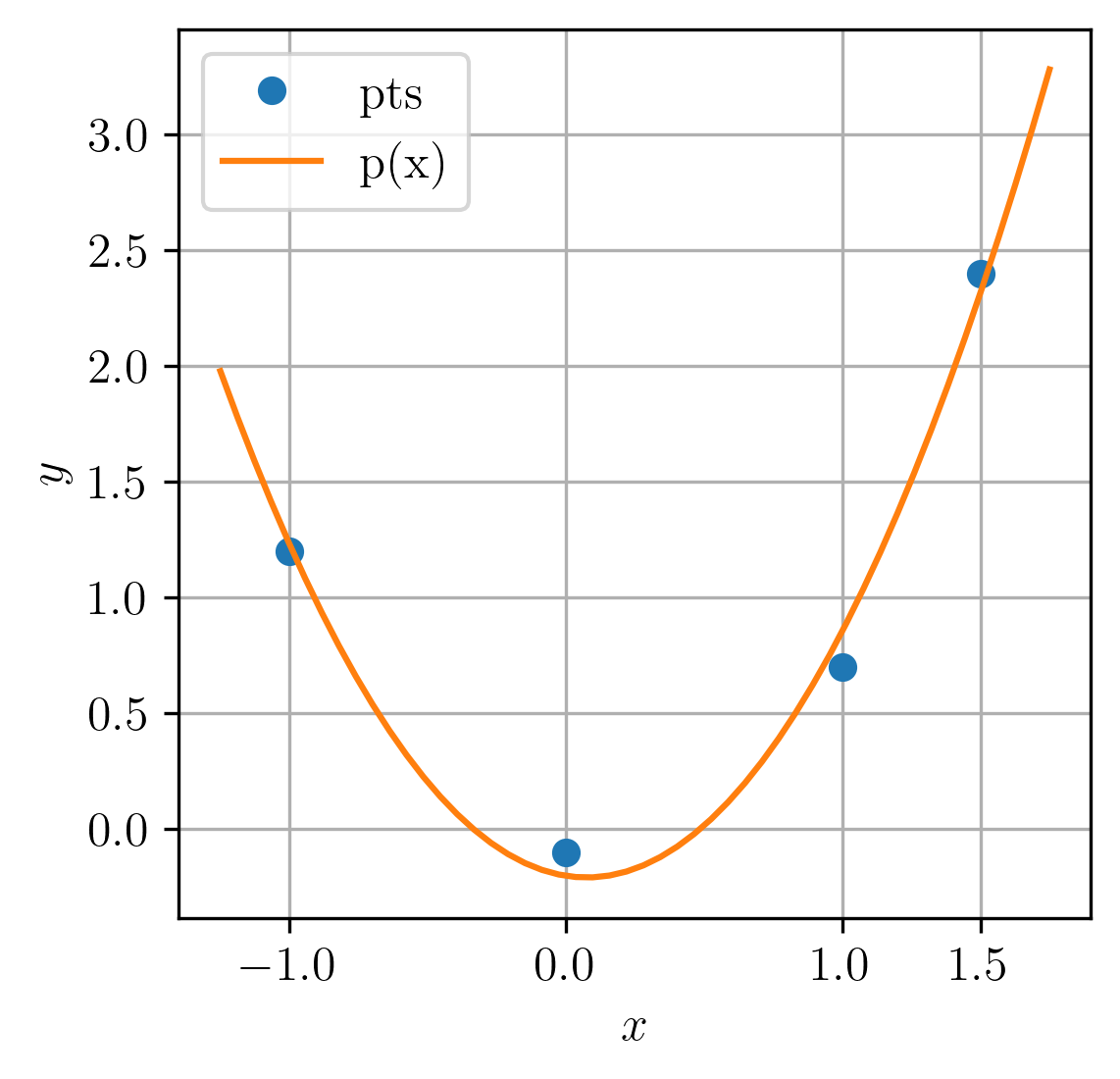
A Figura 6.1 mostra um esboço dos pontos e do polinômio ajustado.

Código 15: mqPoli.py

⬇

1import numpy as np

2import numpy.linalg as npla

4# dados

5xx = np.array([-1.0, 0.0, 1.0, 1.5])

6yy = np.array([1.2, -0.1, 0.7, 2.4])

8# matriz

9m = 3

10n = xx.size

11A = np.empty((n,m))

12A[:,0] = xx**2

13A[:,1] = xx

14A[:,2] = np.ones_like(xx)

16# sol de mq

17p = npla.solve(A.T@A, A.T@yy)

18print(p)

Exemplo 6.1.2 (Ajuste de Curvas).

Consideremos o mesmo conjunto de pontos do exemplo anterior (Exemplo 6.1.1). Aqui, vamos ajustar uma curva da forma

f(x;\boldsymbol{c})=c_{1}\operatorname{sen}(x)+c_{2}\cos(x)+c_{3}

(6.21)

no sentido de mínimos quadrados. Para tanto, formamos a matriz

A:=\begin{bmatrix}\operatorname{sen}(x_{1})&\cos(x_{1})&1\\ \operatorname{sen}(x_{2})&\cos(x_{2})&1\\ \operatorname{sen}(x_{3})&\cos(x_{3})&1\\ \operatorname{sen}(x_{4})&\cos(x_{4})&1\end{bmatrix}

(6.22)

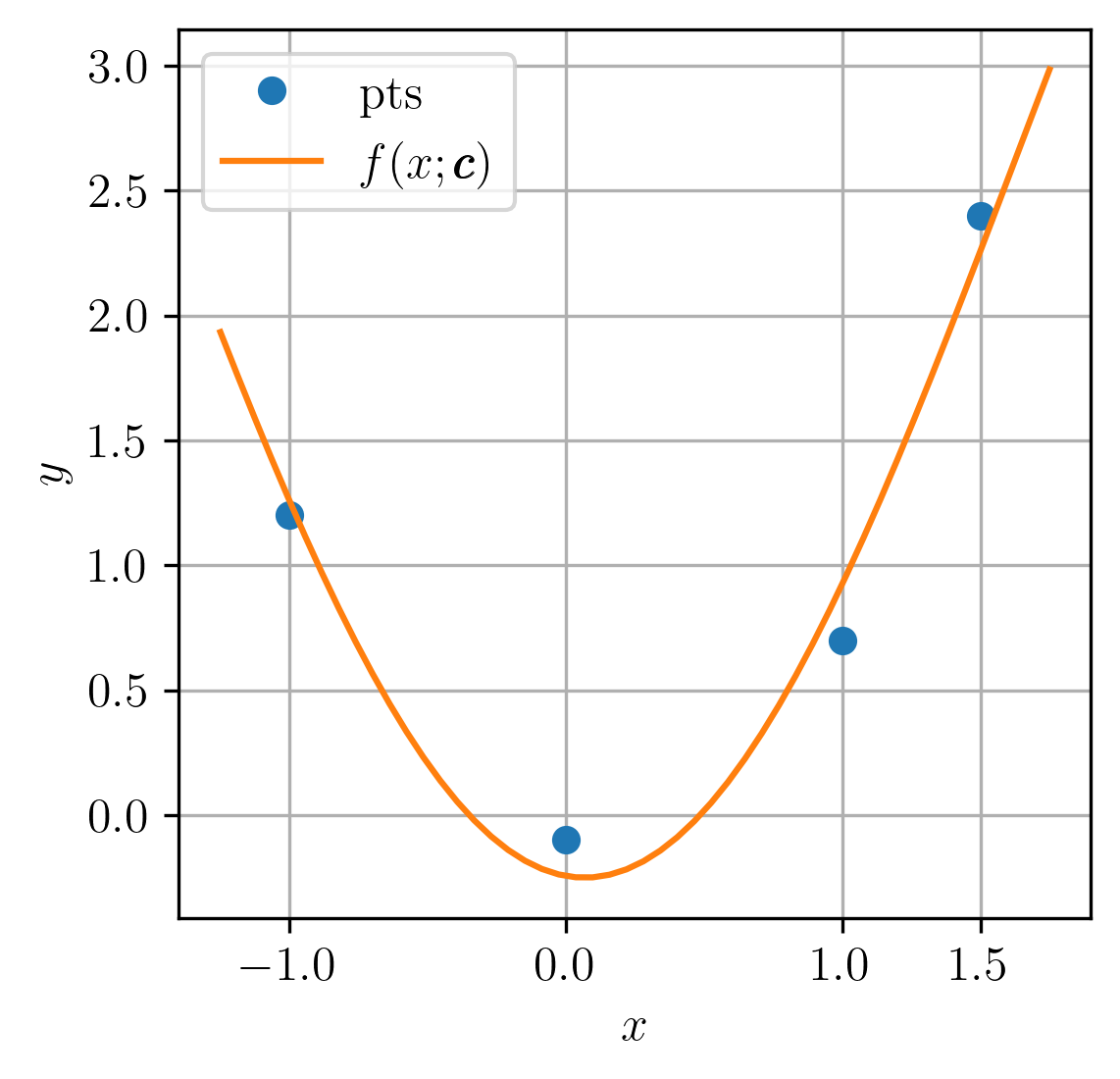
e, então, resolvemos as equações normais (6.15) para o vetor de coeficientes $\boldsymbol{c}=(c_{1},c_{2})$ . Fazendo isso, obtemos $c_{1}=-0,198$ , $c_{2}=-2.906$ e $c_{3}=2.662$ . A Figura 6.2 mostra um esboço da curva ajustada aos pontos dados.

Código 16: mqCurva.py

⬇

1import numpy as np

2import numpy.linalg as npla

4# dados

5xx = np.array([-1.0, 0.0, 1.0, 1.5])

6yy = np.array([1.2, -0.1, 0.7, 2.4])

8# matriz

9m = 3

10n = xx.size

11A = np.empty((n,m))

12A[:,0] = np.sin(xx)

13A[:,1] = np.cos(xx)

14A[:,2] = np.ones_like(xx)

16# sol de mq

17c = npla.solve(A.T@A, A.T@yy)

19def f(x, c=c):

20 y = c[0]*np.sin(x) \

21 + c[1]*np.cos(x) \

22 + c[2]

23 return y

Exemplo 6.1.3 (Um Problema Não-Linear).

Consideramos o problema de ajustar, no sentido de mínimos quadrados, a função

f(x;\boldsymbol{c})=c_{1}e^{c_{2}x}

(6.23)

ao seguinte conjunto de pontos

$i$	$x_{i}$	$y_{i}$
$1$	$-1.0$	$8.0$
$2$	$0.0$	$1.5$
$3$	$1.0$	$0.2$
$4$	$1.5$	$0.1$

Aqui, temos um problema não linear de mínimos quadrados que pode ser transformado em um problema linear fazendo-se

	$\displaystyle y=c_{1}e^{c_{2}x}$		(6.24)
	$\displaystyle\ln y=\ln c_{1}e^{c_{2}x}$		(6.25)
	$\displaystyle\ln y=\ln c_{1}+c_{2}x.$		(6.26)

Isto é, denotando $d_{1}:=\ln c_{1}$ e $d_{2}:=c_{2}$ , o problema se resume a ajustar uma reta $r(x)=d_{1}+d_{2}x$ ao conjunto de pontos $\{(x_{i},\ln y_{i})\}_{i=1}^{4}$ .

Para resolver o problema transformado, formamos a matriz

A:=\begin{bmatrix}1&x_{1}\\ 1&x_{2}\\ 1&x_{3}\\ 1&x_{4}\end{bmatrix}

(6.27)

e, então, resolvemos as equações normais $A^{T}A\boldsymbol{d}=A^{T}\ln\boldsymbol{y}$ , com $\ln\boldsymbol{y}=(\ln y_{1},\ln y_{2},\ln y_{3},\ln y_{4})$ , donde obtemos $d_{1}=0.315$ e $d_{2}=-1.792$ . Das definições de $d_{1}$ e $d_{2}$ , temos

	$\displaystyle c_{2}=d_{2}=-1.792$		(6.28)
	$\displaystyle c_{1}=e^{d_{1}}=1.371.$		(6.29)

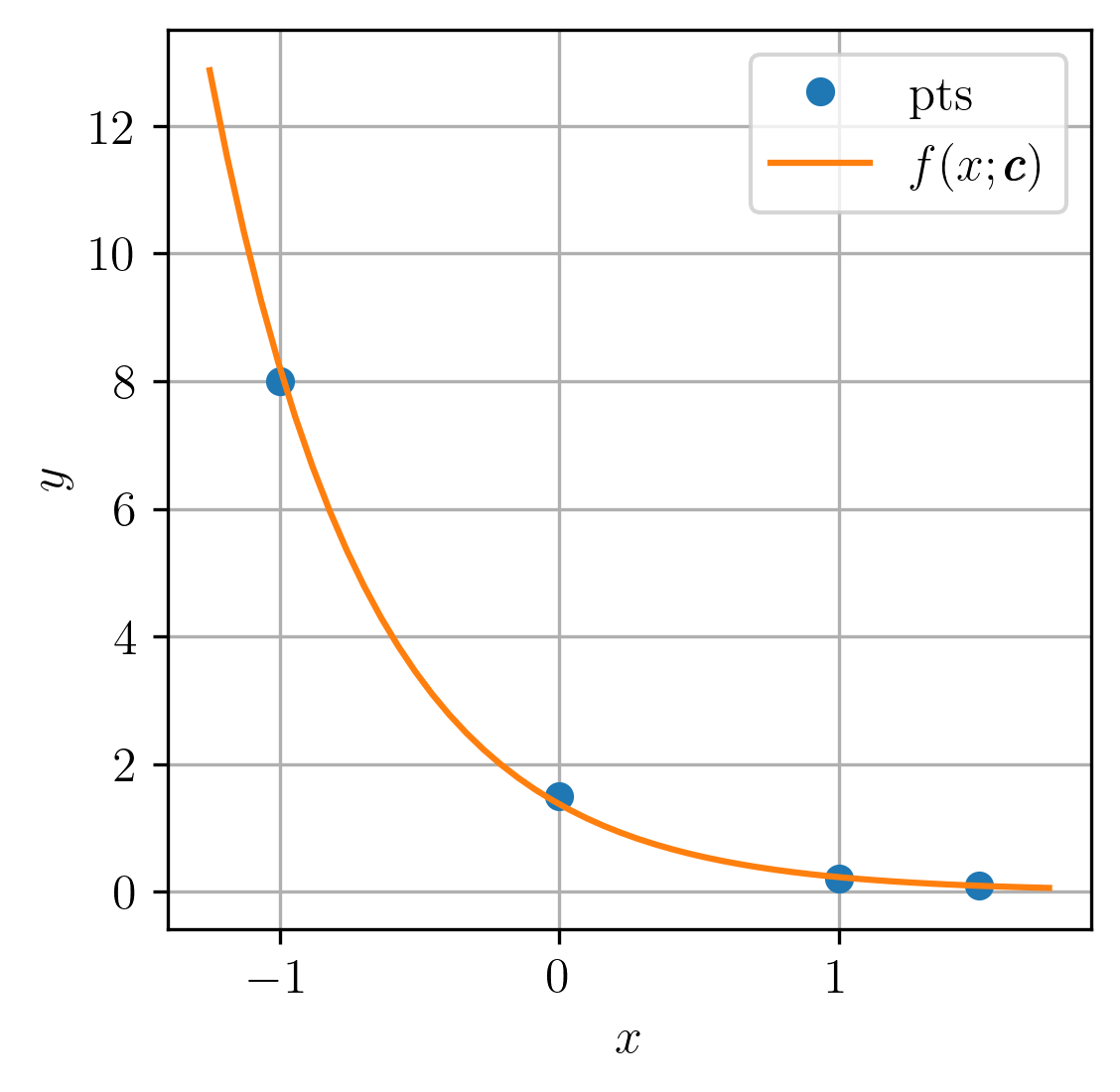
A Figura 6.3 mostra um esboço da curva $f(x;\boldsymbol{c})=c_{1}e^{c_{2}x}$ ajustada aos pontos dados.

6.1.2 Análise Numérica

Em revisão

O problema linear de mínimos quadrados (6.4) reduz-se a resolver o sistema linear (6.15) para $\boldsymbol{c}$ . Isto nos leva a questão de verificar se $A^{T}A$ é invertível.

Teorema 6.1.1.

A matriz $A^{T}A$ é positiva definida se, e somente se, as colunas de $A$ são linearmente independentes.

Demonstração.

Se as colunas de $A$ são linearmente independentes, então $x\neq 0$ implica $Ax\neq 0$ e, equivalentemente, $x^{T}A^{T}\neq 0$ . Portanto, $x\neq 0$ implica $x^{T}A^{T}Ax=\|Ax\|_{2}^{2}>0$ , o que mostra que $A^{T}A$ é positiva definida.

Suponhamos, agora, que as colunas de $A$ não são linearmente independentes. Então, existe $x_{0}\neq 0$ tal que $Ax_{0}=0$ . Mas, então, $x_{0}^{T}A^{T}Ax_{0}=0$ , o que mostra que $A^{T}A$ não é positiva definida. ∎

Este teorema nos fornece uma condição suficiente para a existência (e unicidade) de solução do problema linear de mínimos quadrados. Mais especificamente, se as colunas da matriz $A$ são linearmente independentes, então os coeficientes da função $f(x)$ que melhor ajustam os pontos dados são

c=(A^{T}A)^{-1}A^{T}y.

(6.30)

6.1.3 Exercícios

E. 6.1.1.

Determine a reta $y=c_{1}x+c_{2}$ que melhor se ajusta, no sentido de mínimos quadrados, aos pontos

$i$	$1$	$2$	$3$	$4$	$5$
$x_{i}$	$-2.5$	$-1.3$	$0.2$	$1.7$	$2.3$
$y_{i}$	$3.8$	$1.5$	$-0.7$	$-1.5$	$-3.2$

Por fim, compute a norma $L^{2}$ do resíduo, i.e. $\|r(c)\|_{2}=\|y-(c_{1}x+c_{2})\|_{2}$ para os pontos dados.

Resposta.

$c_{1}=-1.3259$ , $c_{2}=8.66071\mathrm{e}\!-2\!$ , $\|r(c)\|_{2}=1.01390$ .

E. 6.1.2.

Determine o polinômio $y=c_{1}x^{3}+c_{2}x^{2}+c_{3}x+c_{4}$ que melhor se ajusta, no sentido de mínimos quadrados, aos pontos

$i$	$1$	$2$	$3$	$4$	$5$
$x_{i}$	$-2.5$	$-1.3$	$0.2$	$1.7$	$2.3$
$y_{i}$	$3.8$	$0.5$	$2.7$	$1.2$	$-1.3$

Por fim, compute a norma $L^{2}$ do resíduo, i.e. $\|r(c)\|_{2}$ .

Resposta.

$c_{1}=-4.50361\mathrm{e}\!-1\!$ , $c_{2}=-2.78350\mathrm{e}\!-1\!$ , $c_{3}=1.46291$ , $c_{4}=2.09648$ , $\|r(c)\|_{2}=5.71346\mathrm{e}\!-1\!$

E. 6.1.3.

Determine a curva $y=c_{1}\operatorname{sen}x+c_{2}\cos x+c_{3}$ que melhor se ajusta, no sentido de mínimos quadrados, aos pontos

$i$	$1$	$2$	$3$	$4$	$5$
$x_{i}$	$-2.5$	$-1.3$	$0.2$	$1.7$	$2.3$
$y_{i}$	$3.8$	$0.5$	$2.7$	$1.2$	$-1.3$

Por fim, compute a norma $L^{2}$ do resíduo, i.e. $\|r(c)\|_{2}$ .

Resposta.

$c_{1}=-0.86290414$ , $c_{2}=0.36547042$ , $c_{3}=1.4700346$ , $\|r(c)\|_{2}=3.616409$

E. 6.1.4.

Use a transformação $z=\ln y$ para ajustar, no sentido de mínimos quadrados, a curva $y=c_{1}e^{c_{2}(x-c_{3})^{2}}$ aos pontos

$i$	$1$	$2$	$3$	$4$	$5$	$6$
$x_{i}$	$-0.5$	$0.5$	$1.3$	$2,1$	$2.7$	$3,1$
$y_{i}$	$0,1$	$1.2$	$2.7$	$0.9$	$0.2$	$0,1$

Resposta.

$c_{1}=2.10131\mathrm{e}\!+0\!$ , $c_{2}=-9.73859\mathrm{e}\!-1\!$ , $c_{3}=1.25521\mathrm{e}\!+0\!$

Envie seu comentário

As informações preenchidas são enviadas por e-mail para o desenvolvedor do site e tratadas de forma privada. Consulte a Política de Uso de Dados para mais informações. Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

| | | |