Colabore! Saiba mais screen_rotation

Ao navegar por este site , você concorda com a Política de Uso de Dados.

| | | | |

2 Outros sistemas de coordenadas 2 Outros sistemas de coordenadas 3 Cônicas

2.1 Sistema de coordenadas polares

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

No plano, o sistema de coordenadas polares é definido por um ponto de origem (chamado de polo) e um eixo orientado $O x$ (chamado de eixo polar). Veja a Figura 2.1.

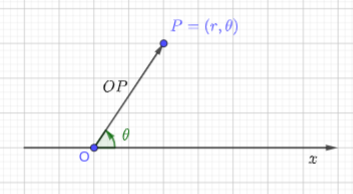
Refer to caption — Figura 2.1: Sistema de coordenadas polares.

Neste sistema, um ponto $P$ de coordenadas polares ${\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}P=(r,\theta)}$ é tal que ${\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}|OP|=r}$ (i.e. a distância do polo ao ponto é $r$ ) e ${\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\theta}$ é o ângulo de $O x$ com $O P$ , medido positivamente no sentido anti-horário.

Exemplo 2.1.1.

Na Figura 2.2, temos a representação dos pontos ${\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}P=(2\sqrt{2},% \frac{\pi}{4})}$ , ${\color[rgb]{1,0,0}\definecolor[named]{pgfstrokecolor}{rgb}{1,0,0}% \pgfsys@color@rgb@stroke{1}{0}{0}\pgfsys@color@rgb@fill{1}{0}{0}A=(2,\frac{2% \pi}{3})}$ e ${\color[rgb]{1,.5,0}\definecolor[named]{pgfstrokecolor}{rgb}{1,.5,0}% \pgfsys@color@rgb@stroke{1}{.5}{0}\pgfsys@color@rgb@fill{1}{.5}{0}B=(\sqrt{2},% \frac{5\pi}{4})}$ no sistema de coordenadas polares.

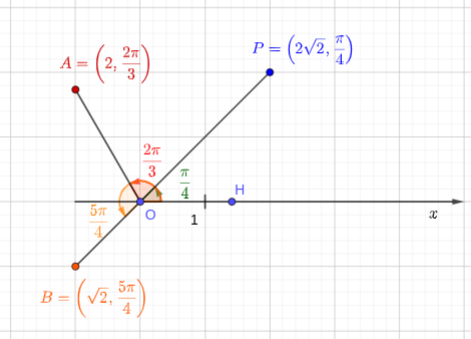
Observação 2.1.1.

Por convenção, as coordenadas polares $(r,\pi+\theta)=(-r,\theta)$ , $r>0$ . Por exemplo, $B=(\sqrt{2},\frac{5\pi}{4})=(-\sqrt{2},\frac{\pi}{4})$ . Veja na Figura 2.2.

2.1.1 Coordenadas cartesianas x polares

Aqui, vamos estudar como podemos converter as coordenadas de um ponto $P$ de coordenadas cartesianas para coordenadas polares e vice-versa. Vamos denotar as coordenadas cartesianas do ponto $P$ por $P=(x_{P},y_{P})$ e suas coordenadas polares por $P=(r,\theta)$ . Veja a Figura 2.3.

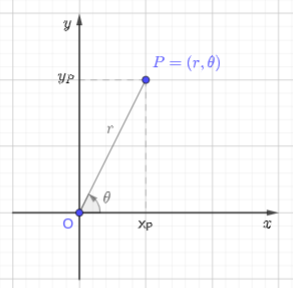
Na Figura 2.3, vamos nos concentrar no triângulo retângulo de vértices $O$ , $(x_{P},0)$ e $P$ . Das relações trigonométricas e do teorema de Pitágoras, temos que

	$\displaystyle\cos\theta=\frac{x_{P}}{r}$		(2.1)
	$\displaystyle\operatorname{sen}\theta=\frac{y_{P}}{r}$		(2.2)
	$\displaystyle r^{2}=x_{P}^{2}+y_{P}^{2}$		(2.3)
	$\displaystyle\operatorname{tg}\theta=\frac{y_{P}}{x_{P}}$		(2.4)

ou, equivalentemente,

	$\displaystyle{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1% }\pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}x_{P}=r\cos\theta}$		(2.5)
	$\displaystyle{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1% }\pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}y_{P}=r% \operatorname{sen}\theta}$		(2.6)
	$\displaystyle{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1% }\pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}r=\sqrt{x_{P}% ^{2}+y_{P}^{2}}}$		(2.7)
	$\displaystyle{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1% }\pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\theta=% \operatorname{arc}\operatorname{tg}\left(\frac{y_{P}}{x_{P}}\right)}$		(2.8)

Exemplo 2.1.2.

Vejamos os seguintes casos:

a)

Conversão de $P=(2\sqrt{2},\frac{\pi}{4})$ em coordenadas polares para coordenadas cartesianas.

No caso de $P=(2\sqrt{2},\frac{\pi}{4}$ temos $r=2\sqrt{2}$ e $\theta=\frac{\pi}{4}$ . Desta forma, as coordenadas cartesianas de $P=(x,y)$ são dadas por

$\displaystyle x$ $\displaystyle=r\cos\theta$ (2.9)

$\displaystyle=2\sqrt{2}\cos\frac{\pi}{4}$ (2.10)

$\displaystyle=2\sqrt{2}\cdot\frac{\sqrt{2}}{2}$ (2.11)

$\displaystyle=2$ (2.12)

$\displaystyle y$ $\displaystyle=r\operatorname{sen}\theta$ (2.13)

$\displaystyle=2\sqrt{2}\operatorname{sen}\frac{\pi}{4}$ (2.14)

$\displaystyle=2\sqrt{2}\cdot\frac{\sqrt{2}}{2}$ (2.15)

$\displaystyle=2$ (2.16)

Logo, $P=(2,2)$ em coordenadas cartesianas. Veja a Figura 2.2.
b)

Conversão de $B=(-\sqrt{3},-1)$ de coordenadas cartesianas para coordenadas polares. Neste caso, temos $x=-\sqrt{3}$ e $y=-1$ e

$\displaystyle r$ $\displaystyle=\sqrt{x^{2}+y^{2}}$ (2.17)

$\displaystyle=\sqrt{(-\sqrt{3})^{2}+(-1)^{2}}$ (2.18)

$\displaystyle=\sqrt{4}$ (2.19)

$\displaystyle=2$ (2.20)

$\displaystyle\theta$ $\displaystyle=\operatorname{arc}\operatorname{tg}\left(\frac{y}{x}\right)$ (2.21)

$\displaystyle=\operatorname{arc}\operatorname{tg}\left(\frac{-1}{-\sqrt{3}}\right)$ (2.22)

$\displaystyle=\operatorname{arc}\operatorname{tg}\left(\frac{\sqrt{3}}{3}\right)$ (2.23)

$\displaystyle=\frac{7\pi}{6}.$ (2.24)

Desta forma, temos que $P=(2,\frac{7\pi}{6})$ em coordenadas polares. Ou, equivalentemente, $P=(-2,\frac{\pi}{6})$ .

Equação de reta que passa pela origem

Em coordenadas polares, uma reta que passa pela origem e tem ângulo de declividade $\theta_{0}$ tem equação

\theta=\theta_{0},

(2.25)

com $r\in\mathbb{R}$ .

Exemplo 2.1.3.

Seja a reta $y=x$ em coordenadas cartesianas. Em coordenadas polares, a equação desta reta é

\theta=\frac{\pi}{4}.

(2.26)

Equação de circunferência com centro na origem

Em coordenadas polares, a circunferência com centro na origem e raio $r_{0}$ tem equação

r=r_{0}.

(2.27)

Exemplo 2.1.4.

Seja a circunferência $x^{2}+y^{2}=4$ em coordenadas cartesianas. Em coordenadas polares, a equação desta circunferência é

r=2.

(2.28)

2.1.2 Exercícios resolvidos

ER 2.1.1.

Obtenha duas representações em coordenadas polares do ponto $A=(-1,0)$ dado em coordenadas cartesianas.

Solução.

O ponto $A=(-1,0)$ tem coordenadas cartesianas $x=-1$ e $y=0$ . Para converter em coordenadas polares $A=(r,\theta)$ , podemos usar

$\displaystyle r^{2}$	$\displaystyle=x^{2}+y^{2}$	(2.29)
$\displaystyle r^{2}$	$\displaystyle=1^{2}+0^{2}$	(2.30)
$\displaystyle r$	$\displaystyle=\pm 1$	(2.31)

$\displaystyle\theta$	$\displaystyle=\operatorname{arc}\operatorname{tg}\left(\frac{y}{x}\right)$	(2.32)
	$\displaystyle=\operatorname{arc}\operatorname{tg}\left(0\right)$	(2.33)
	$\displaystyle=\pi\text{ ou }0.$	(2.34)

Ou seja, em coordenadas polares, temos as representações $A=(1,\pi)$ ou $A=(-1,0)$ .

ER 2.1.2.

Obtenha a representação em coordenadas cartesianas do ponto $B=(2,\frac{\pi}{2})$ dado em coordenadas polares.

Solução.

O ponto $B=(2,\frac{\pi}{2})$ tem coordenadas polares $r=2$ e $\theta=\frac{\pi}{2}$ . Para converter em coordenadas cartesianas $B=(x,y)$ , podemos usar

$\displaystyle x$	$\displaystyle=r\cos\theta$	(2.35)
	$\displaystyle=2\cos\frac{\pi}{2}$	(2.36)
	$\displaystyle=0$	(2.37)

$\displaystyle y$	$\displaystyle=r\operatorname{sen}\theta$	(2.38)
	$\displaystyle=2\operatorname{sen}\frac{\pi}{2}$	(2.39)
	$\displaystyle=2$	(2.40)

Ou seja, em coordenadas cartesianas, temos a representação $B=(0,2)$ .

Exercícios

E. 2.1.1.

Obtenha uma representação em coordenadas polares dos seguintes pontos dados em coordenadas cartesianas:

a)

$A=(-3,3)$
b)

$B=(\frac{3}{2},\frac{\sqrt{3}}{2})$
c)

$C=(\frac{3}{2},-\frac{\sqrt{3}}{2})$

Resposta.

a) $A=(3\sqrt{2},\frac{3\pi}{4})$ ; b) $B=(\sqrt{3},\frac{\pi}{6})$ ; c) $C=(\sqrt{3},\frac{11\pi}{6})$

E. 2.1.2.

Obtenha uma representação em coordenadas cartesianas dos seguintes pontos dados em coordenadas polares:

a)

$A=(2,\frac{\pi}{6})$
b)

$B=(1,\frac{5\pi}{6})$
c)

$C=(-2,\frac{3\pi}{4})$

Resposta.

a) $A=(\sqrt{3},1)$ ; b) $B=(-\frac{\sqrt{3}}{2},\frac{1}{2})$ ; c) $C=(\sqrt{2},-\sqrt{2})$

E. 2.1.3.

Considere a reta de equação $x=0$ em coordenadas cartesianas. Escreva a equação desta reta em coordenadas polares.

Resposta.

$\theta=\frac{\pi}{2}$

E. 2.1.4.

Considere a reta de equação $\theta=\frac{3\pi}{4}$ em coordenadas polares. Escreva a equação desta reta em coordenadas cartesianas.

Resposta.

$y=-x$

E. 2.1.5.

Considere a circunferência de equação $x^{2}+y^{2}=1$ em coordenadas cartesianas. Escreva a equação desta circunferência em coordenadas polares.

Resposta.

$r=1$

E. 2.1.6.

Considere a circunferência de equação $r=\sqrt{2}$ em coordenadas polares. Escreva a equação desta circunferência em coordenadas cartesianas.

Resposta.

$x^{2}+y^{2}=2$

Envie seu comentário

As informações preenchidas são enviadas por e-mail para o desenvolvedor do site e tratadas de forma privada. Consulte a Política de Uso de Dados para mais informações. Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

| | | |

$\displaystyle x$	$\displaystyle=r\cos\theta$	(2.9)
	$\displaystyle=2\sqrt{2}\cos\frac{\pi}{4}$	(2.10)
	$\displaystyle=2\sqrt{2}\cdot\frac{\sqrt{2}}{2}$	(2.11)
	$\displaystyle=2$	(2.12)
$\displaystyle y$	$\displaystyle=r\operatorname{sen}\theta$	(2.13)
	$\displaystyle=2\sqrt{2}\operatorname{sen}\frac{\pi}{4}$	(2.14)
	$\displaystyle=2\sqrt{2}\cdot\frac{\sqrt{2}}{2}$	(2.15)
	$\displaystyle=2$	(2.16)

$\displaystyle r$	$\displaystyle=\sqrt{x^{2}+y^{2}}$	(2.17)
	$\displaystyle=\sqrt{(-\sqrt{3})^{2}+(-1)^{2}}$	(2.18)
	$\displaystyle=\sqrt{4}$	(2.19)
	$\displaystyle=2$	(2.20)
$\displaystyle\theta$	$\displaystyle=\operatorname{arc}\operatorname{tg}\left(\frac{y}{x}\right)$	(2.21)
	$\displaystyle=\operatorname{arc}\operatorname{tg}\left(\frac{-1}{-\sqrt{3}}\right)$	(2.22)
	$\displaystyle=\operatorname{arc}\operatorname{tg}\left(\frac{\sqrt{3}}{3}\right)$	(2.23)
	$\displaystyle=\frac{7\pi}{6}.$	(2.24)