Colabore! Saiba mais screen_rotation

Ao navegar por este site , você concorda com a Política de Uso de Dados.

| | | | |

3.1 Elipse

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

Sejam $F_{1}$ , $F_{2}$ pontos sobre um plano $\pi$ , $c=\frac{1}{2}|F_{1}F_{2}|$ e $a>c$ . Chama-se elipse de focos $F_{1}$ e $F_{2}$ ao conjunto de pontos $P$ tais que

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}|PF_{1}|+|PF_{% 2}|=2a}.

(3.1)

Veja a Figura 3.1.

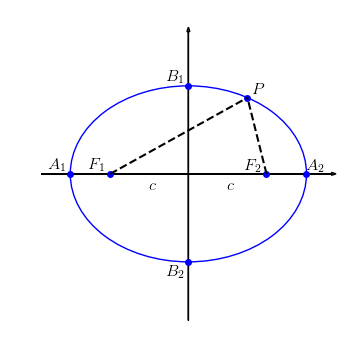
Refer to caption — Figura 3.1: Ilustração de uma elipse de focos $F_{1}$ e $F_{2}$ .

Dada uma tal elipse, identificamos $2c=|F_{1}F_{2}|$ como a distância focal. Os pontos $A_{1}$ e $A_{2}$ de interseção da elipse com a reta que passa pelos focos são chamados de vértices da elipse. O segmento $A_{1}A_{2}$ é chamado de eixo maior da elipse. Observamos que

|A_{1}A_{2}|=2a.

(3.2)

O ponto médio do segmento $F_{1}F_{2}$ é chamado de centro da elipse. Sejam $B_{1}$ e $B_{2}$ os pontos de interseção da elipse com a reta que passa pelo centro da elipse e é perpendicular ao segmento $A_{1}A_{2}$ . Assim sendo, o segmento $B_{1}B_{2}$ é chamado de eixo menor da elipse. Vamos denotar

2b=|B_{1}B_{2}|.

(3.3)

Chamamos de excentricidade da elipse o número

e=\frac{c}{a}.

(3.4)

Notemos que $0\leq e<1$ . Para $e=0$ , temos $c=0$ e, portanto $F_{1}=F_{2}$ . Neste caso, a elipse é a circunferência de centro em $F_{1}$ (ou $F_{2}$ ) e diâmetro $2a$ . No que $e$ tende a $1$ , a elipse tende ao segmento $A_{1}A_{2}$ .

Por fim, notamos que o triângulo $B_{1}OF_{2}$ é retângulo, $|OF_{2}|=c$ , $|F_{2}B_{1}|=a$ e $|OB_{1}|=b$ . Do teorema de Pitágoras segue

b^{2}+c^{2}=a^{2}.

(3.5)

3.1.1 Equação reduzida da elipse

Consideremos o sistema de coordenadas cartesianas. Sejam $F_{1}=(-c,0)$ e $F_{2}=(c,0)$ , $c\geq 0$ , os focos de uma dada elipse (veja a Figura 3.1). Se $P=(x,y)$ é um ponto da elipse, então

|PF_{1}|+|PF_{2}|=2a.

(3.6)

Como

	$\displaystyle\|PF_{1}\|$	$\displaystyle=\sqrt{(x+c)^{2}+y^{2}},$		(3.7)
	$\displaystyle\|PF_{2}\|$	$\displaystyle=\sqrt{(x-c)^{2}+y^{2}},$		(3.8)

temos

\sqrt{(x+c)^{2}+y^{2}}+\sqrt{(x-c)^{2}+y^{2}}=2a,

(3.9)

ou, equivalentemente,

\sqrt{(x+c)^{2}+y^{2}}=2a-\sqrt{(x-c)^{2}+y^{2}}.

(3.10)

Elevando ao quadrado, obtemos

(x+c)^{2}+y^{2}=4a^{2}-4a\sqrt{(x-c)^{2}+y^{2}}+(x-c)^{2}+y^{2}.

(3.11)

Por cancelamento e rearranjo dos termos, obtemos

a\sqrt{(x-c)^{2}+y^{2}}=a^{2}-cx.

(3.12)

Elevando novamente ao quadrado, temos

a^{2}(x-c)^{2}+a^{2}y^{2}=a^{4}-2a^{2}cx+c^{2}x^{2},

(3.13)

donde

a^{2}x^{2}-2a^{2}cx+a^{2}c^{2}+a^{2}y^{2}=a^{4}-2a^{2}cx+c^{2}x^{2}.

(3.14)

Por cancelamento e rearranjo dos termos, obtemos

x^{2}(a^{2}-c^{2})+a^{2}y^{2}=a^{2}(a^{2}-c^{2}).

(3.15)

Como $a>c$ , dividimos por $a^{2}-c^{2}$ e depois por $a^{2}$ para obtemos

\frac{x^{2}}{a^{2}}+\frac{y^{2}}{a^{2}-c^{2}}=1.

(3.16)

Por fim, da equação (3.5), temos $a^{2}-c^{2}=b^{2}$ , o que nos leva a equação reduzida da elipse

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\frac{x^{2}}{a% ^{2}}+\frac{y^{2}}{b^{2}}=1}.

(3.17)

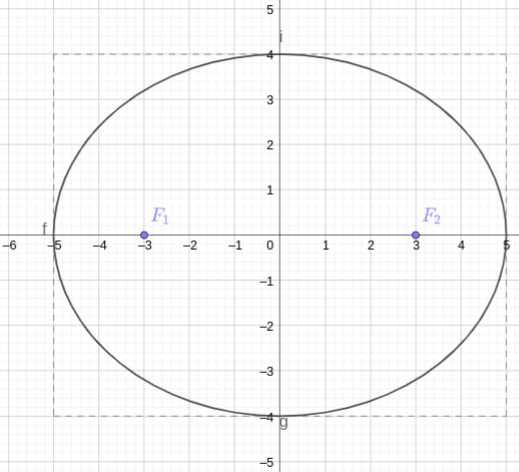
Exemplo 3.1.1.

A Figura 3.2 é um esboço do gráfico da elipse de equação reduzida

\frac{x^{2}}{25}+\frac{y^{2}}{16}=1.

(3.18)

Exercícios resolvidos

ER 3.1.1.

Determine a equação reduzida da elipse de focos $F_{1}=(-3,0)$ , $F_{2}=(3,0)$ e vértices $A_{1}=(-5,0)$ e $A_{2}=(5,0)$ .

Solução.

A equação reduzida tem a forma

\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1,

(3.19)

onde

b^{2}+c^{2}=a^{2}.

(3.20)

Dos focos temos $c=3$ e dos vértices temos $a=5$ . Logo,

$\displaystyle b^{2}$	$\displaystyle=a^{2}-c^{2}$	(3.21)
	$\displaystyle=5^{2}-3^{2}$	(3.22)
	$\displaystyle=25-9$	(3.23)
	$\displaystyle=16.$	(3.24)

Concluímos que a elipse em questão tem equação

\frac{x^{2}}{25}+\frac{y^{2}}{16}=1.

(3.25)

ER 3.1.2.

Determine os focos da elipse de equação

\frac{x^{2}}{16}+\frac{y^{2}}{25}=1.

(3.26)

Solução.

Começamos lembrando que os focos de uma elipse estão localizados sobre seu eixo maior. No caso deste exercício, temos $a=4$ e $b=5$ , logo o eixo maior é $B_{1}B_{2}$ , na mesma direção do eixo das ordenadas $O y$ . Do triângulo retângulo $OA_{2}F_{1}$ temos

b^{2}=a^{2}+c^{2},

(3.27)

veja a Figura 3.3.

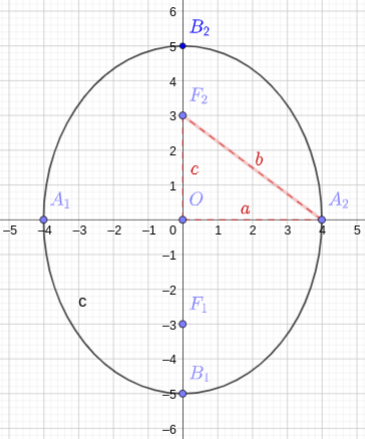
Daí, temos

$\displaystyle c^{2}$	$\displaystyle=b^{2}-a^{2}$	(3.28)
	$\displaystyle=25-16$	(3.29)
	$\displaystyle=9$	(3.30)
$\displaystyle c$	$\displaystyle=3.$	(3.31)

Concluímos que os focos são $F_{1}=(0,-3)$ e $F_{2}=(0,3)$ .

Exercícios

E. 3.1.1.

Faça um esboço da elipse de equação reduzida

\frac{x^{2}}{9}+\frac{y^{2}}{4}=1.

(3.32)

Resposta.

E. 3.1.2.

Faça um esboço da elipse de equação reduzida

\frac{x^{2}}{4}+\frac{y^{2}}{9}=1.

(3.33)

Resposta.

E. 3.1.3.

Determine os vértices (sobre o eixo maior) das seguintes elipses:

a)

$\displaystyle\frac{x^{2}}{9}+\frac{y^{2}}{4}=1$
b)

$\displaystyle x^{2}+\frac{y^{2}}{16}=1$

Resposta.

a) $(-3,0)$ , $(3,0)$ ; b) $(0,-4)$ , $(0,4)$

E. 3.1.4.

Determine os focos das seguintes elipses:

a)

$\displaystyle\frac{x^{2}}{9}+\frac{y^{2}}{4}=1$
b)

$\displaystyle x^{2}+\frac{y^{2}}{16}=1$

Resposta.

a) $(-\sqrt{5},0)$ , $(\sqrt{5},0)$ ; b) $(0,\sqrt{15})$ , $(0,\sqrt{15})$

E. 3.1.5.

Forneça a equação reduzida da elipse de focos $F_{1}=(-1,0)$ , $F_{2}=(1,0)$ e vértices $A_{1}=(-\sqrt{2},0)$ , $A_{2}=(\sqrt{2},0)$ .

Resposta.

$\displaystyle\frac{x^{2}}{2}+y^{2}=1$

E. 3.1.6.

Forneça a equação reduzida da elipse de focos $F_{1}=(0,-2)$ , $F_{2}=(0,2)$ e vértices $B_{1}=(0,-\sqrt{5})$ , $B_{2}=(0,\sqrt{5})$ .

Resposta.

$\displaystyle x^{2}+\frac{y^{2}}{5}=1$

Envie seu comentário

As informações preenchidas são enviadas por e-mail para o desenvolvedor do site e tratadas de forma privada. Consulte a Política de Uso de Dados para mais informações. Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

| | | |