Colabore! Saiba mais screen_rotation

Ao navegar por este site , você concorda com a Política de Uso de Dados.

| | | | |

3 Programação Estruturada 3.2 Instruções de Ramificação 4 Funções

3.3 Instruções de Repetição

Compre o e-book deste material aqui!

Estruturas de repetição permitem a execução de um bloco de código várias vezes. O número de vezes que o bloco é repetido pode depender de uma condição lógica (instrução while) ou do número de itens de um objeto iterável (instruçãofor).

3.3.1 Instrução while

A instrução while permite a repetição condicional de um bloco de código. Em Python, sua sintaxe é

⬇

1bloco_anterior

2while condição:

3 bloco

4bloco_posterior

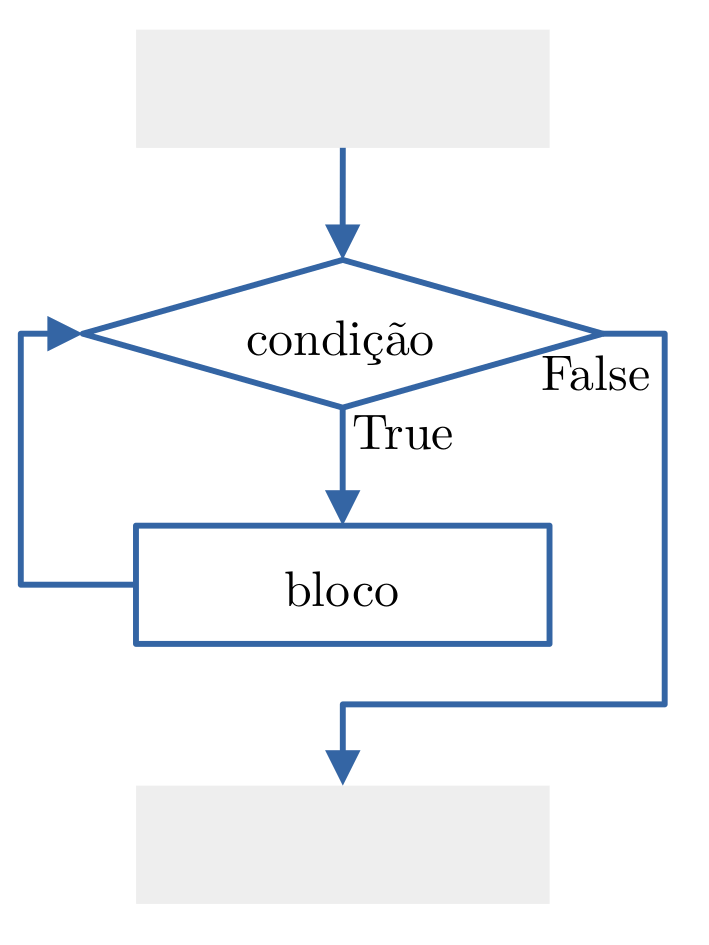
Refer to caption — Figura 3.9: Fluxograma da estrutura de repetição while.

Exemplo 3.3.1.

(Somatório com while) O seguinte código, computa o somatório

	$\displaystyle s$	$\displaystyle=\sum_{i=1}^{n}i$		(3.20)
		$\displaystyle=1+2+3+\cdots+n.$		(3.21)

⬇

1n = int(input('Digite um número natural n:\n'))

3soma = 0

4i = 1

5while (i <= n):

6 soma = soma + i

7 i = i + 1

9print(f'1 + ... + {n} = {soma}')

Exemplo 3.3.2.

(Aproximando a $\sqrt{x}$ .) O método de Heron³⁰³⁰endnote: ³⁰Heron de Alexandria, 10 - 80, matemático grego. Fonte: Wikipédia: Heron de Alexandria. é um algoritmo para o cálculo aproximado da raiz quadrada de um dado número $x$ , i.e. $\sqrt{x}$ . Consiste na iteração³¹³¹endnote: ³¹Aqui, assumimos a aproximação inicial $s^{(0)}=1$ , mas qualquer outro número não negativo pode ser usado.

	$\displaystyle r^{(0)}$	$\displaystyle=1,$		(3.22)
	$\displaystyle r^{(k+1)}$	$\displaystyle=\frac{1}{2}\left(r^{(k)}+\frac{x}{r^{(k)}}\right),$		(3.23)

para $k=0,1,2,\ldots,n-1$ , onde $n$ é o número de iterações calculadas. Para $x\geq 0$ fornecido por usuária(o), o seguinte código computa a aproximação $r^{(5)}\approx\sqrt{x}$ .

⬇

1x = float(input('Digite um número não negativo para x:\n'))

2r = 1

3k = 0

4print(f'{k}: {r}')

5while (k < 5):

6 r = 0.5*(r + x/r)

7 k = k + 1

8 print(f'{k}: {r}')

9print(f'sqrt({x}) = {r}')

break

A instrução break permite interromper um bloco de repetição e sair dele no momento em que ela é alcançada.

Exemplo 3.3.3.

No Exemplo 3.3.2, podemos observar que as aproximações $s^{(k)}\approx\sqrt{x}$ vão se tornando muito próximas umas das outras conforme as iterações convergem. Dessa observação, faz sentido que interrompamos as computações no momento em que a $k+1$ -ésima iterada satisfaça

\left|r^{(k+1)}-r^{(k)}\right|<\texttt{tol}

(3.24)

para alguma tolerância tol desejada.

⬇

1max_iter = 50

2tol = 1e-15

4x = float(input('Digite um número não negativo para x:\n'))

6r0 = 1

7k = 0

8print(f'{k}: {r}')

9while (k < max_iter):

10 k = k + 1

11 r = 0.5*(r0 + x/r0)

12 print(f'{k}: {r}')

13 if (abs(r-r0) < tol):

14 break

15 r0 = r

16print(f'sqrt({x}) = {r}')

3.3.2 Instrução for

A instrução for iteração de um bloco de código para todos os itens de um dado objeto. Em Python, sua sintaxe é

⬇

1bloco_anterior

2for x in Iterável:

3 bloco

4bloco_posterior

Pode-se percorrer qualquer objeto iterável (set, tuple, list, dict, etc.). Em cada iteração, o índice x toma um novo item do objeto. A repetição termina quando todos os itens do objeto tiverem sido escolhidos. No caso de iteráveis ordenados (tuple, list, dict, etc.), os itens são iterados na mesma ordem em que estão alocados no objeto.

Exemplo 3.3.4.

O seguinte código, computa a média aritmética do conjunto de números

A=\{1,3,5,7,9\}.

(3.25)

⬇

1soma = 0

2for x in {1,3,5,7,9}:

3 soma = soma + x

4media = soma/5

5print(f'média = {media}')

range

A função range([start], stop, [step]), retorna uma sequência iterável de números inteiros, com início em start (padrão start=0), passo step (padrão step=1) e limite em stop.

Exemplo 3.3.5.

Estudamos os seguinte casos:

a)

Imprime, em ordem crescente, os primeiros $11$ números naturais.

⬇

1for i in range(11):

2 print(i)
b)

Imprime, em ordem crescente, os números naturais contidos de $3$ a $13$ , inclusive.

⬇

1for i in range(3,14):

2 print(i)
c)

Imprime, em ordem crescente, os números naturais ímpares contidos de $3$ a $13$ , inclusive.

⬇

1for i in range(3,14,2):

2 print(i)
d)

Imprime, em ordem decrescente, os números naturais contidos de $3$ a $13$ , inclusive.

⬇

1for i in range(13,2,-1):

2 print(i)

Exemplo 3.3.6.

(Somatório com for.) No Exemplo 3.3.1, computados

s=\sum_{i=1}^{n}i

(3.26)

usando um laço while. Aqui, apresentamos uma nova versão do código com a instrução for.

⬇

1n = int(input('Digite um número natural n:\n'))

2soma = 0

3for i in range(1,n+1):

4 soma = soma + i

5print(f'1 + ... + {n} = {soma}')

Exemplo 3.3.7.

No Exemplo 3.3.3, apresentamos um código para o cálculo aproximado de $\sqrt{x}$ pelo Método de Heron. Aqui, temos uma nova versão com a instrução for no lugar do laço while.

⬇

1max_iter = 50

2tol = 1e-15

4x = float(input('Digite um número não negativo para x:\n'))

6r0 = 1

7k = 0

8print(f'{k}: {r}')

9for k in range(max_iter):

10 r = 0.5*(r0 + x/r0)

11 print(f'{k+1}: {r}')

12 if (abs(r-r0) < tol):

13 break

14 r0 = r

15print(f'sqrt({x}) = {r}')

3.3.3 Exercícios

E. 3.3.1.

Faça o fluxograma do código apresentado no Exemplo 3.3.1. Também, desenvolva uma versão melhorada do código, que verifica se o valor de $n$ digitado pela(o) usuária(o) é não negativa. Caso afirmativo, computa o somatório, noutro caso apenas imprime mensagem de que o $n$ deve ser não negativo.

Resposta.

⬇

1n = int(input('Digite um número natural n:\n'))

2if (n >= 0):

3 soma = 0

4 i = 1

5 while (i <= n):

6 soma = soma + i

7 i = i + 1

9 print(f'1 + ... + {n} = {soma}')

10else:

11 print('ERRO: n deve ser não negativo.')

E. 3.3.2.

Faça um fluxograma para o código apresentado no Exemplo 3.3.4.

Resposta.

Dica: consulte o fluxograma apresentado no Exemplo 3.1.3.

E. 3.3.3.

Crie um objeto do tipo range para cada uma das seguintes sequências:

1.

Sequência crescente de todos os números inteiros de $0$ até $99$ , inclusive.
2.

Sequência crescente de todos os números pares de $-5$ até $15$ .
3.

Sequência decrescente de todos os números de $100$ a $0$ , inclusive.
4.

Sequência decrescente de todos os números múltiplos de $3$ entre $17$ e $-3$ .

Resposta.

a)

range(100)
b)

range(-4,15,2)
c)

range(100,-1,-1)
d)

range(15,-4,-3)

E. 3.3.4.

Considere o somatório entre dois números inteiros $n\leq m$

	$\displaystyle s$	$\displaystyle=\sum_{i=n}^{m}i$		(3.27)
		$\displaystyle=n+(n+1)+(n+2)+\cdots+m$		(3.28)

Com números informados pela(o) usuária(o), escreva duas versões de códigos para a computação desse somatório:

a)

Usando a instrução while.
b)

Usando a instrução for.

Resposta.

⬇

1n = int(input('Digite um número inteiro n:\n'))

2m = int(input('Digite um número inteiro m>n:\n'))

3soma = 0

4i = n

5while (i<=m):

6 soma = soma + i

7 i = i + 1

8print(f'n+...+m = {soma}')

⬇

1n = int(input('Digite um número inteiro n:\n'))

2m = int(input('Digite um número inteiro m>n:\n'))

3soma = 0

4for i in range(n,m+1):

5 soma = soma + i

6print(f'n+...+m = {soma}')

E. 3.3.5.

A série harmônica é

\sum_{k=1}^{\infty}\frac{1}{k}=1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}+\cdots

(3.29)

Com $n$ fornecido por usuária(o), crie códigos que computem o valor da soma harmônica

s=\sum_{k=1}^{n}\frac{1}{k}=1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}.

(3.30)

a)

Use uma estrutura de repetição while.
b)

Use uma estrutura de repetição for.

Resposta.

⬇

1n = int(input('Digite um número natural n:\n'))

2s = 0

3k = 1

4while (k <= n):

5 s = s + 1/k

6 k = k + 1

7print(s)

⬇

1n = int(input('Digite um número natural n:\n'))

2s = 0

3for k in range(n):

4 s = s + 1/(k+1)

5print(s)

E. 3.3.6.

O cálculo do logaritmo natural pode ser feito pela seguinte série de potências

\ln(1+x)=\sum_{k=1}^{\infty}(-1)^{k+1}\frac{x^{k}}{k}

(3.31)

Desenvolva um código que compute a aproximação do $ln(2)$ dada por

\ln(2)=\sum_{k=1}^{n}\frac{(-1)^{k+1}}{k}

(3.32)

com $n>=1$ número inteiro fornecido por usuária(o).

a)

Use uma estrutura de repetição while.
b)

Use uma estrutura de repetição for.

Resposta.

⬇

1n = int(input('Digite um número natural n >= 1: '))

3s = 0

4k = 1

5while (k <= n):

6 s += (-1)**(k+1)/k

7 k += 1

8print(f'ln(2) aprrox. {s}')

⬇

1n = int(input('Digite um número natural n >= 1: '))

3s = 0

4for k in range(1, n+1):

5 s += (-1)**(k+1)/k

6 k += 1

7print(f'ln(2) aprrox. {s}')

E. 3.3.7.

O fatorial de um número natural é definido pelo produtório

	$\displaystyle n!$	$\displaystyle:=\prod_{k=1}^{n}k$		(3.33)
		$\displaystyle=1\cdot 2\cdot 3\cdot(n-1)\cdot n$		(3.34)

e $0!:=1$ . Com $n$ informado por usuária(o), crie códigos para computar $n!$ usando:

a)

uma estrutura de repetição while.
b)

uma estrutura de repetição for.

Resposta.

⬇

1n = int(input('Digite um número natural n:\n'))

2fat = 1

3k = 1

4while (k < n):

5 k = k + 1

6 fat = fat * k

7print(f'{n}! = {fat}')

⬇

1n = int(input('Digite um número natural n:\n'))

2fat = 1

3for k in range(1,n+1):

4 fat = fat * k

5print(f'{n}! = {fat}')

E. 3.3.8.

O número de Euler³²³²endnote: ³²Leonhard Paul Euler, 1707-1783, matemático e físico suíço. Fonte: Wikipédia: Ronald Fisher. é tal que

	$\displaystyle e$	$\displaystyle:=\sum_{k=0}^{\infty}\frac{1}{n!}$		(3.35)
		$\displaystyle=\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots+\frac{1}{n!}+\cdots$		(3.36)

Com $n$ fornecido por usuária(o), desenvolva um código que computa a aproximação

e\approx e^{(n)}=\sum_{k=0}^{n}\frac{1}{n!}.

(3.37)

Qual o número $n$ tal que $\left|e^{(n)}-e^{(n-1)}\right|<10^{-15}$ ?

Resposta.

⬇

1n = int(input('Digite um número natural n:\n'))

2fat = 1

3e = 1

4for k in range(1,n+1):

5 fat = fat * k

6 e = e + 1/fat

7print(f'e = {e}')

E. 3.3.9.

Com $n\geq 1$ número natural fornecido por usuária(o), crie um código que verifique se $n$ é um número primo.

Resposta.

⬇

1n = int(input('Digite um número natural n>=1:\n'))

2primo = True

3for i in range(2, n//2+1):

4 if (n % i == 0):

5 primo = False

6 break

7print(f'{n} é primo? {primo}')

Envie seu comentário

As informações preenchidas são enviadas por e-mail para o desenvolvedor do site e tratadas de forma privada. Consulte a Política de Uso de Dados para mais informações. Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

| | | |