Colabore! Saiba mais screen_rotation

Ao navegar por este site , você concorda com a Política de Uso de Dados.

| | | | |

3 Programação Estruturada 3.1 Estruturas de um Programa 3.3 Instruções de Repetição

3.2 Instruções de Ramificação

Compre o e-book deste material aqui!

Instruções de ramificação permitem a seleção de blocos de processamento com base em condições lógicas.

3.2.1 Instrução if

A instrução de ramificação if permite a seleção de um bloco de processamento com base em uma condição lógica.

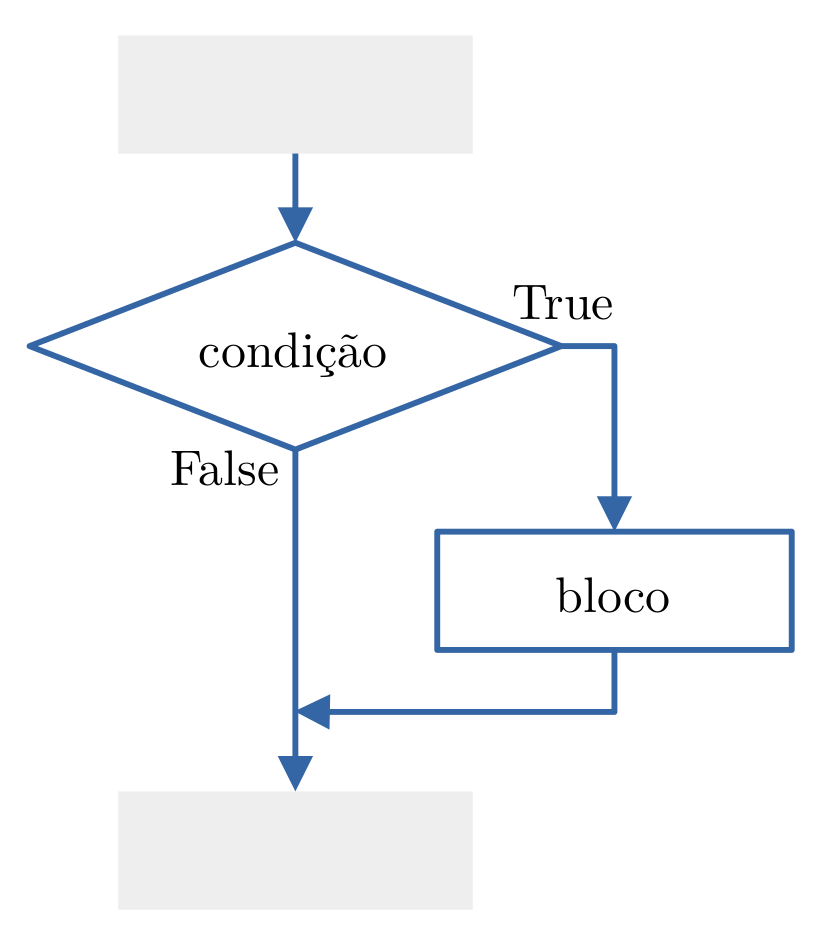
Refer to caption — Figura 3.6: Fluxograma de uma ramificação if.

Em Python, a instrução if tem a seguinte sintaxe:

⬇

1bloco_anterior

2if (condição):

3 bloco_0

4bloco_posterior

Se a condição é verdadeira (True), o bloco (linha 3) é executado. Caso contrário, este bloco não é executado e o fluxo de processamento salta da linha 2 para a linha 6. O escopo do bloco if é determinado pela indentação do código.

Exemplo 3.2.1.

Seja o polinômio de segundo grau

p(x)=ax^{2}+bx+c.

(3.4)

No caso de existirem, o seguinte código computa as raízes distintas de $p(x)$ para os coeficientes informados pela(o) usuária(o).

⬇

1# entrada de dados

2a = float(input('Digite o valor de a:\n'))

3b = float(input('Digite o valor de b:\n'))

4c = float(input('Digite o valor de c:\n'))

6# discriminante

7delta = b**2 - 4*a*c

9# raízes

10if (delta > 0):

11 # raízes distintas

12 x1 = (-b - delta**0.5)/(2*a)

13 x2 = (-b + delta**0.5)/(2*a)

14 print(f'x_1 = {x1}')

15 print(f'x_2 = {x2}')

Escopo de Variáveis

O escopo de uma variável é a região em que ela permanece alocada. O escopo de variáveis alocadas fora do bloco if inclui este bloco, mas variáveis alocadas no bloco if não permanecem alocadas fora deste.

Exemplo 3.2.2.

No Exemplo 3.2.1, o escopo da variável delta inicia-se na linha 7 e permanece válido ao longo do resto do programa. Já, o escopo da variável x1 compreende somente as linhas 12-15 e, análogo para a variável x2.

3.2.2 Instrução if-else

A instrução if-else permite a escolha de um bloco ou outro, exclusivamente, com base em uma condição lógica.

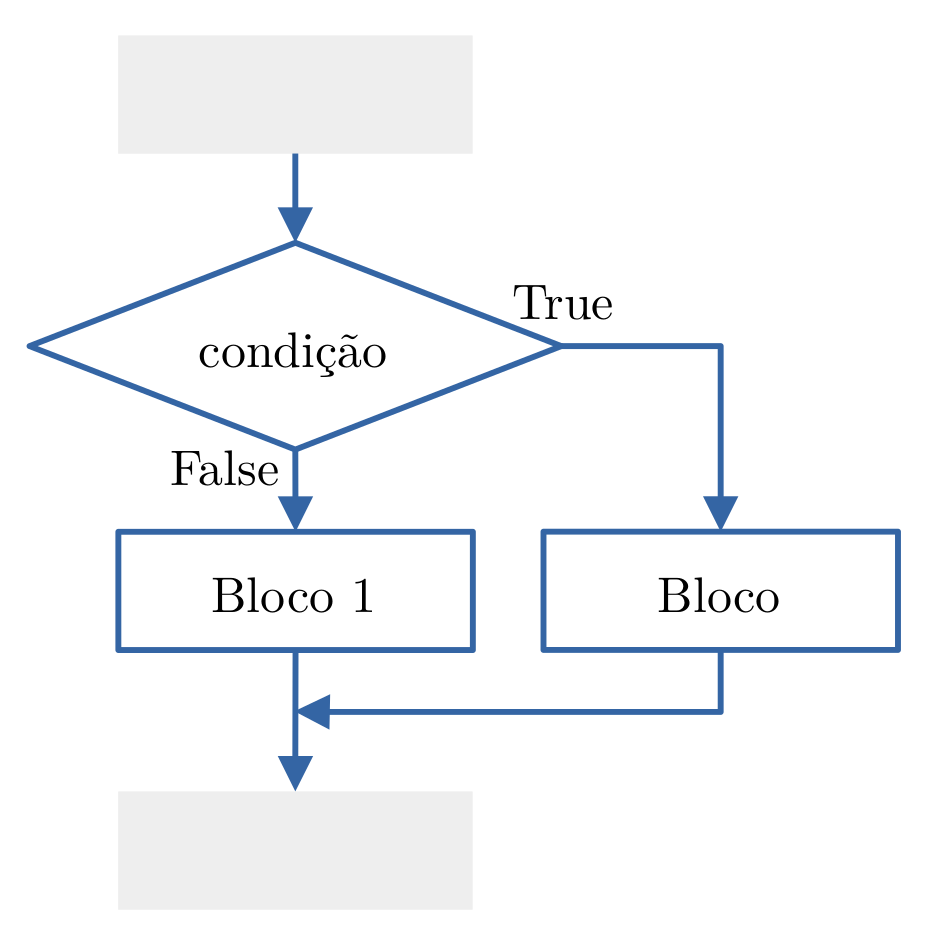
Em Python, a instrução if-else tem a seguinte sintaxe:

⬇

1bloco_anterior

2if (condição):

3 bloco_0

4else:

5 bloco_1

6bloco_posterior

Se a condição for verdadeira (True) o bloco 0 é executado, senão o bloco 1 é executado.

Exemplo 3.2.3.

Seja o polinômio de segundo grau

p(x)=ax^{2}+bx+c.

(3.5)

Se existirem, o seguinte código computa as raízes reais do polinômio, senão imprime mensagem informado que elas não são reais.

⬇

1# entrada de dados

2a = float(input('Digite o valor de a:\n'))

3b = float(input('Digite o valor de b:\n'))

4c = float(input('Digite o valor de c:\n'))

6# discriminante

7delta = b**2 - 4*a*c

9# raízes

10if (delta >= 0):

11 x1 = (-b - delta**0.5)/(2*a)

12 x2 = (-b + delta**0.5)/(2*a)

13 print(f'x_1 = {x1}')

14 print(f'x_2 = {x2}')

15else:

16 print('Não tem raízes reais.')

Instrução if-else em Linha

Por praticidade, Python também tem a sintaxe if-else em linha:

⬇

1x = valor if True else outro_valor

Exemplo 3.2.4.

O valor absoluto de um número real $x$ é

|x|:=\left\{\begin{array}[]{ll}x&,x\geq 0,\\ -x&,x<0\end{array}\right.

(3.6)

O seguinte código, computa o valor absoluto²⁹²⁹endnote: ²⁹Python tem a função abs para computar o valor absoluto de um número. de um número dado por usuária(o).

⬇

1x = float(input('Digite o valor de x:\n'))

2abs_x = x if (x>=0) else -x

3print(f'|x| = {abs_x}')

3.2.3 Instrução if-elif

A instrução if-elif permite a seleção condicional de blocos, sem impor a necessidade da execução de um deles.

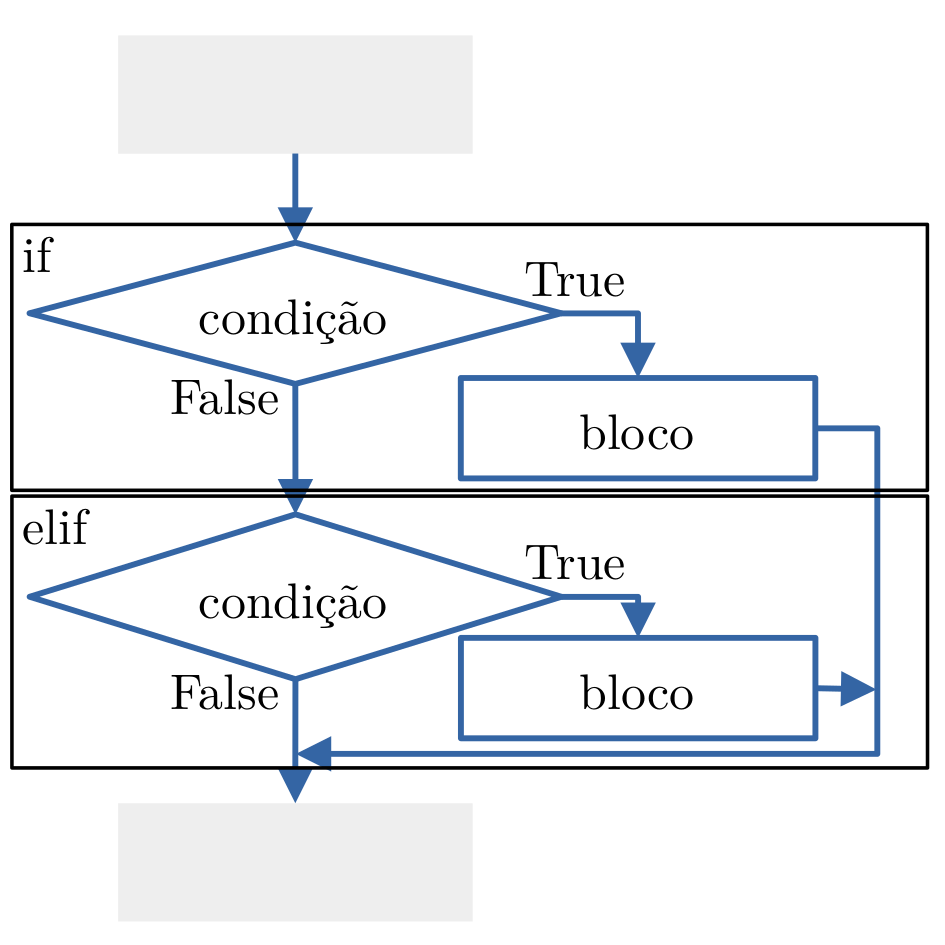
Em Python, a instrução if-elif tem a seguinte sintaxe:

⬇

1bloco_anterior

2if (condição_0):

3 bloco_0

4elif (condição 1):

5 bloco_1

6bloco posterior

Se a condição_0 for verdadeira (True), o bloco_0 é executado. Senão, se a condição_1 for verdadeira (True) o bloco_1 é executado. No caso de ambas as condições serem falsas (False), os blocos bloco_0 e bloco_1 não são executados e o fluxo de processamento segue a partir da linha 6.

Exemplo 3.2.5.

Seja o polinômio de segundo grau

p(x)=ax^{2}+bx+c.

(3.7)

Conforme o caso, o seguinte código computa a raiz dupla do polinômio ou suas raízes reais distintas, a partir dos coeficientes informados pela(o) usuária(o).

⬇

1# entrada de dados

2a = float(input('Digite o valor de a:\n'))

3b = float(input('Digite o valor de b:\n'))

4c = float(input('Digite o valor de c:\n'))

6# discriminante

7delta = b**2 - 4*a*c

9# raízes

10if (delta > 0):

11 x1 = (-b - delta**0.5)/(2*a)

12 x2 = (-b + delta**0.5)/(2*a)

13 print('Raízes reais distintas:')

14 print(f'x_1 = {x1}')

15 print(f'x_2 = {x2}')

16elif (delta == 0):

17 print('Raiz dupla:')

18 x = -b/(2*a)

19 print(f'x_1 = x_2 = {x}')

3.2.4 Instrução if-elif-else

A instrução if-elif-else permite a seleção condicional de blocos, sendo que ao menos um bloco será executado. Em Python, sua sintaxe é:

⬇

1bloco_anterior

2if (condição_0):

3 bloco_0

4elif (condição_1):

5 bloco_1

6else:

7 bloco_2

8bloco posterior

Se a condição_0 for verdadeira (True), então o bloco_0 é executado. Senão, se a condição_1 for verdadeira (True), então o bloco_1 é executado. Senão, o bloco_2 é executado.

Exemplo 3.2.6.

Seja o polinômio de segundo grau

p(x)=ax^{2}+bx+c.

(3.8)

Conforme o caso (raízes reais distintas, raiz dupla ou raízes complexas), o seguinte código computa as raízes desse polinômio, a partir dos coeficientes informados pela(o) usuária(o).

⬇

1# entrada de dados

2a = float(input('Digite o valor de a:\n'))

3b = float(input('Digite o valor de b:\n'))

4c = float(input('Digite o valor de c:\n'))

6# discriminante

7delta = b**2 - 4*a*c

9# raízes

10if (delta > 0):

11 # raízes distintas

12 x1 = (-b - delta**0.5)/(2*a)

13 x2 = (-b + delta**0.5)/(2*a)

14 print('Raízes reais distintas:')

15 print(f'x_1 = {x1}')

16 print(f'x_2 = {x2}')

17elif (delta == 0):

18 # raiz dupla

19 x = -b/(2*a)

20 print('Raiz dupla:')

21 print(f'x_1 = x_2 = {x}')

22else:

23 # raízes complexas

24 # parte real

25 rea = -b/(2*a)

26 # parte imaginária

27 img = (-delta)**0.5/(2*a)

28 x1 = rea - img*1j

29 x2 = rea + img*1j

30 print('Raízes complexas:')

31 print(f'x_1 = {x1}')

32 print(f'x_2 = {x2}')

3.2.5 Múltiplos Casos

Pode-se encadear instruções if-elif-elif-...-elif[-else] para a seleção condicional entre múltiplos blocos.

Exemplo 3.2.7.

Sejam as circunferências de equações:

	$\displaystyle c_{1}$	$\displaystyle:(x-a_{1})^{2}+(y-b_{1})^{2}=r_{1},$		(3.9)
	$\displaystyle c_{2}$	$\displaystyle:(x-a_{1})^{2}+(y-b_{1})^{2}=r_{2}.$		(3.10)

Conforme entradas dadas por usuária(o), o seguinte código informa se um dado ponto $(x,y)$ pertence: à interseção dos discos determinados por $c_{1}$ e $c_{2}$ , apenas ao disco determinado por $c_{1}$ , apenas ao disco determinado por $c_{2}$ ou a nenhum desses discos.

⬇

1# entrada de dados

2print('c1: (x-a1)**2 + (y-b1)**2 = r1')

3a1 = float(input('Digite o valor de a1:\n'))

4b1 = float(input('Digite o valor de b1:\n'))

5r1 = float(input('Digite o valor de r1:\n'))

6print('c2: (x-a2)**2 + (y-b2)**2 = r1')

7a2 = float(input('Digite o valor de a2:\n'))

8b2 = float(input('Digite o valor de b2:\n'))

9r2 = float(input('Digite o valor de r2:\n'))

10print('Ponto de interesse (x,y).')

11x = float(input('Digite o valor de x:\n'))

12y = float(input('Digite o valor de y:\n'))

14# pertence ao disco c1?

15c1 = (x-a1)**2 + (y-b1)**2 <= r1

16# pertence ao disco c2?

17c2 = (x-a2)**2 + (y-b2)**2 <= r2

19# imprime resultado

20if (c1 and c2):

21 print(f'({x}, {y}) pertence à interseção dos discos.')

22elif (c1):

23 print(f'({x},{y}) pertence ao disco c1.')

24elif (c2):

25 print(f'({x},{y}) pertence ao disco c2.')

26else:

27 print(f'({x},{y}) não pertence aos discos.')

3.2.6 Exercícios

E. 3.2.1.

Seja a equação de reta

ax+b=0.

(3.11)

Dados coeficientes $a\neq 0$ e $b$ informados por usuária(o), crie um código que imprime o ponto de interseção dessa reta com o eixo das abscissas. O código não deve tentar computar o ponto no caso de $a=0$ .

Resposta.

⬇

1# entrada de dados

2a = float(input('Digite o valor de a:\n'))

3b = float(input('Digite o valor de b:\n'))

5# computação

6if (a != 0):

7 x = -b/a

8 y = a*x + b

9 print(f'Intercepta eixo-x em: ({x}, {y}).')

E. 3.2.2.

Considere o seguinte código.

⬇

1n = int(input('Digite um número inteiro:\n')

2if (n % 2 == 0):

3 m = 1

4n = n + m

5print(n)

A ideia é que, se $n$ for ímpar, o código imprime $n$ , caso contrário, imprime $n+1$ . Este código contém erro. Identifique e explique-o, então proponha uma versão funcional.

Resposta.

⬇

1n = int(input('Digite um número inteiro:\n')

2m = 0

3if (n % 2 == 0):

4 m = 1

5n = n + m

6print(n)

E. 3.2.3.

Considere o seguinte algoritmo/pseudocódigo para verificar se um dado número inteiro $n$ é par ou ímpar.

0.

Início.
1.

Usuária(o) informa o valor inteiro $n$ .
2.
Se o resto da divisão de $n$ por $2$ for igual a zero, então faça:
- 2.1.
  
  Imprime a mensagem: “ $n$ é par.”.
3.
Senão, faça:
- 3.1
  
  Imprime a mensagem: “ $n$ é ímpar”.
4.

Fim.

Faça um fluxograma para esse algoritmo e implemente-o.

E. 3.2.4.

Considere a equação da circunferência

c:(x-a)^{2}+(y-b)^{2}=r^{2}.

(3.12)

Com dados informados por usuária(o), desenvolva um código que informe se um dado ponto $(x,y)$ pertence ou não ao disco determinado por $c$ .

Resposta.

⬇

1# entrada de dados

2print('Circunferência c:')

3a = float(input('Digite o valor de a:\n'))

4b = float(input('Digite o valor de b:\n'))

5r = float(input('Digite o valor de r:\n'))

6print('Ponto (x, y):')

7x = float(input('Digite o valor de x:\n'))

8y = float(input('Digite o valor de y:\n'))

10# resultado

11if ((x-a)**2 + (y-b)**2 <= r**2):

12 print(f'({x}, {y}) pertence ao disco.')

13else:

14 print(f'({x}, {y}) não pertence ao disco.')

E. 3.2.5.

Sejam informadas por usuária(o) os coeficientes das retas

	$\displaystyle r_{1}$	$\displaystyle:a_{1}x+b_{1}=0,$		(3.13)
	$\displaystyle r_{2}$	$\displaystyle:a_{2}x+b_{2}=0.$		(3.14)

Crie um código que informe se as retas são paralelas. Caso contrário, o código imprime o ponto de interseção delas.

Resposta.

⬇

1# entrada de dados

2print('r1: a1*x + b1 = 0')

3a1 = float(input('Digite o valor de a1:\n'))

4b1 = float(input('Digite o valor de b1:\n'))

5print('r2: a2*x + b2 = 0')

6a2 = float(input('Digite o valor de a2:\n'))

7b2 = float(input('Digite o valor de b2:\n'))

9# resultado

10if (a1 == a2):

11 print('r1 // r2')

12else:

13 x = (b1-b2)/(a2-a1)

14 y = a1*x + b1

15 print('Ponto de interseção: ({x}, {y}).')

E. 3.2.6.

Refaça o código do Exercício 3.2.5 de forma a incluir o caso em que as retas sejam coincidentes. Ou seja, o código deve informar os seguintes casos: retas paralelas não coincidentes, retas coincidentes ou, caso contrário, ponto de interseção das retas.

Resposta.

⬇

1# entrada de dados

2print('r1: a1*x + b1 = 0')

3a1 = float(input('Digite o valor de a1:\n'))

4b1 = float(input('Digite o valor de b1:\n'))

5print('r2: a2*x + b2 = 0')

6a2 = float(input('Digite o valor de a2:\n'))

7b2 = float(input('Digite o valor de b2:\n'))

9# resultado

10if (a1 == a2):

11 if (b1 == b2):

12 print('r1 = r2')

13 else:

14 print('r1 // r2 e r1 != r2')

15else:

16 x = (b1-b2)/(a2-a1)

17 y = a1*x + b1

18 print('Ponto de interseção: ({x}, {y}).')

E. 3.2.7.

Sejam a parábola de equação

a_{1}x^{2}+a_{2}x+a_{3}=0

(3.15)

e a reta

b_{1}x+b_{2}=0.

(3.16)

Conforme os coeficientes dados por usuária(o), desenvolva um código que imprime o(s) ponto(s) de interseção da reta com a parábola. O código deve avisar os casos em que: há apenas um ponto, há dois pontos ou não há ponto de interseção.

Resposta.

⬇

1# entrada de dados

2print('Coeficientes da parábola')

3print('a1*x**2 + a2*x + a3 = 0')

4a1 = float(input('Digite o valor de a1:\n'))

5a2 = float(input('Digite o valor de a2:\n'))

6a2 = float(input('Digite o valor de a3:\n'))

8print('Coeficientes da reta')

9print('b1*x + b2 = 0')

10b1 = float(input('Digite o valor de b1:\n'))

11b2 = float(input('Digite o valor de b2:\n'))

13# discriminante da equação

14# a1*x**2 + (a2-b1)*x + (a3-b2) = 0

15delta = (a2-b1)**2 - 4*a1*(a3-b2)

17# ponto(s) de interseção

18if (delta == 0):

19 x = (b1-a2)/(2*a1)

20 y = b1*x + b2

21 print('Ponto de interseção:')

22 print(f'({x}, {y})')

23elif (delta > 0):

24 x1 = ((b1-a2) - delta**2)/(2*a1)

25 y1 = b1*x1 + b2

26 x2 = ((b1-a2) + delta**2)/(2*a1)

27 y2 = b1*x2 + b2

28 print('Pontos de interseção:')

29 print(f'({x1}, {y1}), ({x2}, {y2})')

30else:

31 print('Não há ponto de interseção.')

E. 3.2.8.

Com dados informados por usuária(o), sejam as circunferências de equações

	$\displaystyle c_{1}$	$\displaystyle:(x-a_{1})^{2}+(y-b_{1})^{2}=r_{1}^{2},$		(3.17)
	$\displaystyle c_{2}$	$\displaystyle:(x-a_{2})^{2}+(y-b_{2})^{2}=r_{2}^{2}.$		(3.18)

Desenvolva um código que informe a(o) usuária(o) dos seguintes casos: $c_{1}$ e $c_{2}$ são coincidentes, $c_{1}\cap c_{2}$ tem dois pontos, $c_{1}\cap c_{2}$ tem somente um ponto, $c_{1}\cap c_{2}=\emptyset$ .

Resposta.

⬇

1# entrada de dados

2print('c1: (x-a1)**2 + (y-b1)**2 = r1**2')

3a1 = float(input('Digite o valor de a1:\n'))

4b1 = float(input('Digite o valor de b1:\n'))

5r1 = float(input('Digite o valor de r1:\n'))

6print('c2: (x-a2)**2 + (y-b2)**2 = r2**2')

7a2 = float(input('Digite o valor de a2:\n'))

8b2 = float(input('Digite o valor de b2:\n'))

9r2 = float(input('Digite o valor de r2:\n'))

11# verificações

12if (((a1==a2) and (b1==b2)) and (r1==r2)):

13 print('c1 = c2')

14else:

15 # distância entre os centros

16 dist = ((a2-a1)**2 + (b2-b1)**2)**0.5

17 if (abs(dist - (r1+r2)) < 1e-15):

18 print('c1 & c2 têm um único ponto de interseção.')

19 elif (dist < r1+r2):

20 print('c1 & c2 têm dois pontos de interseção.')

21 else:

22 print('c1 & c2 não tem ponto de interseção.')

E. 3.2.9.

Crie uma calculadora simples. A(o) usuária(o) entra com dois números decimais x e y e uma das seguintes operações: +, -, * ou /. Então, o código imprime o resultado da operação.

Resposta.

⬇

1# entrada de dados

2x = float(input('Digite o valor de x:\n'))

3op = input('Digite uma das operações +, -, * ou /:\n')

4y = float(input('Digite o valor de y:\n'))

6# calcula

7if (op == '+'):

8 print(f'{x} ' + op + f' {y} = {x+y}')

9elif (op == '-'):

10 print(f'{x} ' + op + f' {y} = {x-y}')

11elif (op == '*'):

12 print(f'{x} ' + op + f' {y} = {x*y}')

13elif (op == '/'):

14 print(f'{x} ' + op + f' {y} = {x/y}')

15else:

16 print('Desculpa, não entendi!')

E. 3.2.10.

Informado um ponto $P=(x,y)$ por usuária(o), desenvolva um código que verifique se $P$ está entre as curvas $x=-1$ , $x=2$ , $y=x^{2}$ e $y=x+2$ . Consulte a figura abaixo.

Resposta.

⬇

1print('P = (x,y)')

2x = float(input('Digite o valor de x: '))

3y = float(input('Digite o valor de y: '))

5if (((x >= -1.) and (x <= 2)) and

6 (y >= x**2) and (y <= x+2)):

7 print(f'P = ({x}, {y}) está entre as curvas.')

8else:

9 print(f'P = ({x}, {y}) não está entre as curvas.')

E. 3.2.11.

Considere um polinômio da forma

p(x)=(x-a)(bx^{2}+cx+d).

(3.19)

Desenvolva um código para a computação das raízes de $p(x)$ , sendo os coeficientes $a$ , $b$ , $c$ e $d$ (números decimais) informados por usuária(o).

Resposta.

⬇

1print('p(x) = (x-a)(bx^2 + cx + d)')

2# entrada de dados

3a = float(input('Digite o valor de a: '))

4b = float(input('Digite o valor de b: '))

5c = float(input('Digite o valor de c: '))

6d = float(input('Digite o valor de d: '))

8# cálculo das raízes

9x1 = a

10print(f'x1 = {x1}')

11if (b != 0.):

12 delta = c**2 - 4*b*d

13 x2 = (-c - delta**0.5)/(2*b)

14 x3 = (-c + delta**0.5)/(2*b)

15 print(f'x2 = {x2}')

16 print(f'x3 = {x3}')

17elif (c != 0.):

18 x2 = -d/c

19 print(f'x2 = {x2}')

Envie seu comentário

As informações preenchidas são enviadas por e-mail para o desenvolvedor do site e tratadas de forma privada. Consulte a Política de Uso de Dados para mais informações. Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

| | | |