Matemática Numérica III

1 Sistemas Lineares 1 Sistemas Lineares 1.2 Matrizes esparsas

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

1.1 Matrizes bandas

A solução de um sistema linear em que a matriz dos coeficientes é uma matriz banda pode ser eficiente computada com um adequado formato de armazenamento. Uma matriz $A$ é uma matriz banda quando seus elementos não nulos estão dispostos em apenas algumas de suas diagonais. A largura da banda é o número de diagonais não nulas $d$ , incluindo a diagonal principal. A largura inferior $l$ (superior $u$ ) é o número de diagonais não nulas abaixo (acima) da diagonal principal ( $d=l+u+1$ ).

Exemplo 1.1.1.(Matriz tridiagonal)

Uma matriz tridiagonal é uma matriz banda com largura da banda $d=3$ , largura inferior $l=1$ e largura superior $u=1$ .

Para fixarmos as ideias, considere o seguinte sistema linear

	$\displaystyle a_{0,0}x_{0}+a_{0,1}x_{1}=b_{0}$		(1.1)
	$\displaystyle a_{1,0}x_{0}+a_{1,1}x_{1}+a_{1,2}x_{2}=b_{1}$		(1.2)
	$\displaystyle a_{2,0}x_{0}+a_{2,1}x_{1}+a_{2,2}x_{2}+a_{2,3}x_{3}=b_{2}$		(1.3)
	$\displaystyle a_{3,1}x_{1}+a_{3,2}x_{2}+a_{3,3}x_{3}+a_{3,4}x_{4}=b_{3}$		(1.4)
	$\displaystyle\qquad\vdots$
	$\displaystyle a_{n-1,n-3}x_{n-3}+a_{n-1,n-2}x_{n-2}+a_{n-1,n-1}x_{n-1}=b_{n-1}$		(1.5)

ou seja, um sistema linear $n\times n$ cuja a matriz dos coeficientes é uma matriz banda com largura da banda $d=3$ , largura inferior $l=1$ e largura superior $u=2$ . A matriz dos coeficientes é dada por

A=\begin{bmatrix}\boldsymbol{a_{0,0}}&a_{0,1}&0&0&\cdots&0\\ a_{1,0}&\boldsymbol{a_{1,1}}&a_{1,2}&0&\cdots&0\\ a_{2,0}&a_{2,1}&\boldsymbol{a_{2,2}}&a_{2,3}&\cdots&0\\ 0&a_{3,1}&a_{3,2}&\boldsymbol{a_{3,3}}&\cdots&0\\ \vdots&\vdots&\vdots&\vdots&\ddots&\vdots\\ 0&0&0&a_{n-1,n-3}&a_{n-1,n-2}&\boldsymbol{a_{n-1,n-1}}\end{bmatrix}.

(1.6)

Notemos que a matriz $A$ pode ser armazenada de forma compacta como

A_{b}=\begin{bmatrix}*&a_{0,1}&a_{1,2}&\cdots&a_{n-3,n-2}&a_{n-2,n-1}\\ \boldsymbol{a_{0,0}}&\boldsymbol{a_{1,1}}&\boldsymbol{a_{2,2}}&\cdots&% \boldsymbol{a_{n-2,n-2}}&\boldsymbol{a_{n-1,n-1}}\\ a_{1,0}&a_{2,1}&a_{3,2}&\cdots&a_{n-1,n-2}&*\\ a_{2,0}&a_{3,1}&a_{4,2}&\cdots&*&*\\ \end{bmatrix}

(1.7)

Exemplo 1.1.2.(Equaçao de Poisson 1D)

Consideremos a equação de Poisson¹¹1Siméon Denis Poisson, 1781 - 1840, matemático francês. Fonte: Wikipédia: Siméon Denis Poisson. unidimensional e com condições de contorno de Dirichlet homogêneas

	$\displaystyle-u^{\prime\prime}(x)=f(x),$		(1.8)
	$\displaystyle u(0)=0,$		(1.9)
	$\displaystyle u(1)=0.$		(1.10)

para $x\in(0,1)$ . Assumindo a fonte $f(x)=\pi^{2}\operatorname{sen}(\pi x)$ , a solução analítica é dada por $u(x)=\operatorname{sen}(\pi x)$ (verifique!).

Vamos empregar o método de diferenças finitas para computar uma aproximação para a sua solução. Começamos assumindo uma malha uniforme de $n$ nodos $x_{i}=ih$ , com tamanho de malha $h=1/(n-1)$ , $i=0,1,\dotsc,n-1$ . Empregando a fórmula de diferenças central, encontramos o seguinte problema discreto associado

	$\displaystyle u_{0}=0,$		(1.11)
	$\displaystyle-\frac{1}{h^{2}}u_{i-1}+\frac{2}{h^{2}}u_{i}-\frac{1}{h^{2}}u_{i+% 1}=f(x_{i}),$		(1.12)
	$\displaystyle u_{n-1}=0,$		(1.13)

para $i=1,2,\dotsc,n-2$ . Este é um sistema linear $A\boldsymbol{u}=h^{2}\boldsymbol{b}$ em que a matriz dos coeficientes é a matriz tridiagonal $n\times n$

A=\begin{bmatrix}1&0&0&\cdots&0&0\\ -1&2&-1&\cdots&0&0\\ 0&-1&2&\cdots&0&0\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\ 0&0&0&\cdots&2&-1\\ 0&0&0&\cdots&0&1\end{bmatrix}.

(1.14)

O vetor das incógnitas é $\boldsymbol{u}=(u_{0},u_{1},\dotsc,u_{n-1})$ e o vetor dos termos constantes é $h^{2}\boldsymbol{b}=h^{2}(f(x_{0}),f(x_{1}),\dotsc,f(x_{n-1}))$ . Note que a matriz $A$ pode ser armazenada de forma compacta como

A_{b}=\begin{bmatrix}*&1&0&\cdots&0&0\\ 1&2&2&\cdots&2&1\\ -1&-1&-1&\cdots&-1&*\end{bmatrix}

(1.15)

O Código 1 computa a solução de um sistema linear tridiagonal usando o método de eliminação gaussiana (verifique!).

Código 1: solve_tribanded.py

⬇

1def solve_tribanded(ab, b):

2 a = ta.copy()

3 x = b.copy()

4 # eliminação

5 for i in range(1,n):

6 w = a[2,i-1]/a[1,i-1]

7 a[1,i] -= w * a[0,i]

8 x[i] -= w * x[i-1]

9 # resolve

10 x[n-1] = x[n-1]/a[1,n-1]

11 for i in range(n-2,-1,-1):

12 x[i] = (x[i] - a[0,i+1]*x[i+1])/a[1,i]

13 return x

Exemplo 1.1.3.(Equação de Poisson 2D)

Consideramos o seguinte problema de Poisson²²2Siméon Denis Poisson, 1781 - 1840, matemático francês. Fonte: Wikipédia: Siméon Denis Poisson. 2D

	$\displaystyle-\Delta u=f(x,y),\leavevmode\nobreak\ (x,y)\in(0,\pi)^{2},$		(1.16)
	$\displaystyle u(0,y)=0,\leavevmode\nobreak\ y\in[0,\pi],$		(1.17)
	$\displaystyle u(\pi,y)=0,\leavevmode\nobreak\ y\in[0,\pi],$		(1.18)
	$\displaystyle u(x,0)=0,\leavevmode\nobreak\ x\in[0,\pi],$		(1.19)
	$\displaystyle u(x,\pi)=0,\leavevmode\nobreak\ x\in[0,\pi],$		(1.20)

onde, $\Delta:=\left(\frac{\partial^{2}}{\partial x^{2}},\frac{\partial^{2}}{\partial y% ^{2}}\right)$ é o operador laplaciano³³3Pierre-Simon Laplace, 1749 - 1827, matemático francês. Fonte: Wikipédia: Pierre-Simon Laplace.. Para fixarmos as ideias, vamos assumir

f(x,y)=\operatorname{sen}(x)\operatorname{sen}(y)

(1.21)

Vamos empregar o método de diferenças finitas para computar uma aproximação para a sua solução. Começamos assumindo uma malha uniforme de $n^{2}$ nodos

	$\displaystyle x_{i}=(i-1)h$		(1.22)
	$\displaystyle y_{j}=(j-1)h$		(1.23)

com tamanho de malha $h=\pi/(n-1)$ , $i=1,2,\dotsc,n$ e $j=1,2,\dotsc,n$ . Empregando a fórmula de diferenças central, encontramos o seguinte problema discreto associado

	$\displaystyle u_{i,1}=u_{1,j}=0$		(1.24)
	$\displaystyle-\frac{1}{h^{2}}u_{i-1,j}-\frac{1}{h^{2}}u_{i,j-1}+\frac{4}{h^{2}% }u_{i,j}$
	$\displaystyle\qquad-\frac{1}{h^{2}}u_{i+1,j}-\frac{1}{h^{2}}u_{i,j+1}=f(x_{i},% y_{j})$		(1.25)
	$\displaystyle u_{i,n}=u_{n,j}=0$		(1.26)

Este é um sistema linear $n^{2}\times n^{2}$ . Tomando em conta as condições de contorno, ele pode ser reduzido a um sistema $(n-2)^{2}\times(n-2)^{2}$

Aw=b

(1.27)

usando a enumeração das incógnitas

(i,j)\rightarrow k=i-1+(j-2)(n-2),

(1.28)

i.e.

u_{i,j}=w_{k=i-1+(j-2)(n-2)}

(1.29)

para $i,j=2,\dotsc,n-2$ . Consulte a Figura 1.1 para uma representação da enumeração em relação a malha.

Figura 1.1: Representação da enumeração das incógnitas referente ao problema de Poisson 2D. Exemplo 1.1.3.

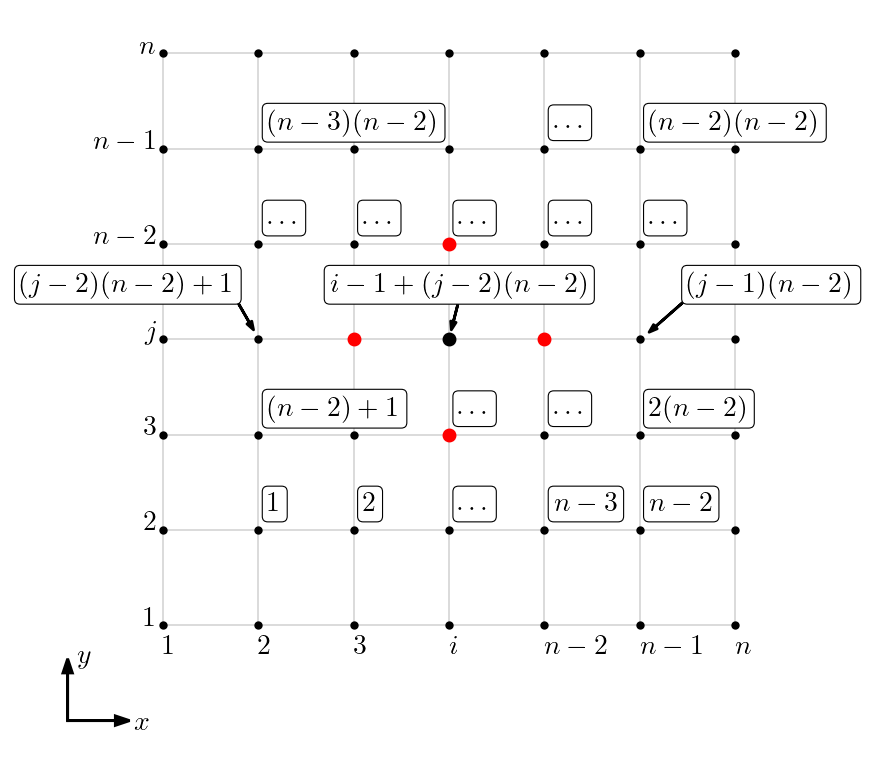
Afim de obtermos uma matriz diagonal dominante, vamos ordenar as equações do sistema discreto como segue

•

$j=2$ , $i=2$ :

$4w_{k}-w_{k+1}-w_{k+n-2}=h^{2}f_{i,j}$ (1.30)
•

$j=2$ , $i=3,\dotsc,n-2$ :

$-w_{k-1}+4w_{k}-w_{k+1}-w_{k+n-2}=h^{2}f_{i,j}$ (1.31)
•

$j=2$ , $i=n-1$ :

$-w_{k-1}+4w_{k}-w_{k+n-2}=h^{2}f_{i,j}$ (1.32)
•

$j=3,\dotsc,n-2$ , $i=2$ :

$-w_{k-(n-2)}+4w_{k}-w_{k+1}-w_{k+n-2}=h^{2}f_{i,j}$ (1.33)
•

$j=3,\dotsc,n-2$ , $i=3,\dotsc,n-2$ :

$-w_{k-1}-w_{k-(n-2)}+4w_{k}-w_{k+1}-w_{k+n-2}=h^{2}f_{i,j}$ (1.34)
•

$j=3,\dotsc,n-2$ , $i=n-1$ :

$-w_{k-1}-w_{k-(n-2)}+4w_{k}-w_{k+n-2}=h^{2}f_{i,j}$ (1.35)
•

$j=n-1$ , $i=2$ :

$-w_{k-(n-2)}+4w_{k}-w_{k+1}=h^{2}f_{i,j}$ (1.36)
•

$j=n-1$ , $i=3,\dotsc,n-2$ :

$-w_{k-1}-w_{k-(n-2)}+4w_{k}-w_{k+1}=h^{2}f_{i,j}$ (1.37)
•

$j=n-1$ , $i=n-1$ :

$-w_{k-1}-w_{k-(n-2)}+4w_{k}=h^{2}f_{i,j}$ (1.38)

Com isso, temos um sistema com matriz com 5 bandas, consulte a Figura 1.2.

Figura 1.2: Matriz do sistema discreto construído no Exemplo 1.1.3.

O Código 2 implementa a montagem do sistema linear e sua solução usando a função solve_banded da biblioteca scipy.linalg. Verifique o código e compare a solução com a solução analítica $u(x,y)=\operatorname{sen}(x)\operatorname{sen}(y)$ .

Código 2: poisson2d.py

⬇

1import numpy as np

2from scipy.linalg import solve_banded

5# malha

6n = 11

7h = 1/(n-1)

9xx = np.linspace(0, 1, n)

10yy = np.linspace(0, 1, n)

12# fonte

13def f(x,y):

14 return 2 * np.pi**2 * np.sin(np.pi*x) * np.sin(np.pi*y)

16# sistema discreto

17u = l = n-2

18ab = np.zeros((u+l+1, (n-2)**2))

19b = np.empty((n-2)**2)

21# matrix banded index

22def ind(k,l):

23 return u + k - l, l

25for j in np.arange(2,n):

26 for i in np.arange(2,n):

28 # enumeração dos nodos computacionais

29 k = i-2 + (j-2)*(n-2)

31 # vetor b

32 b[k] = h**2 * f(xx[i-1], yy[j-1])

34 # matriz ab

35 ab[ind(k,k)] = 4.

37 if (j == 2):

38 if (i == 2):

39 ab[ind(k,k+1)] = -1.

40 ab[ind(k,k+n-2)] = -1.

41 elif (i <= n-2):

42 ab[ind(k,k-1)] = -1.

43 ab[ind(k,k+1)] = -1.

44 ab[ind(k,k+n-2)] = -1.

45 else: # i == n-1

46 ab[ind(k,k-1)] = -1.

47 ab[ind(k,k+n-2)] = -1.

48 elif (j <= n-2):

49 if (i == 2):

50 ab[ind(k,k-(n-2))] = -1.

51 ab[ind(k,k+1)] = -1.

52 ab[ind(k,k+n-2)] = -1.

53 elif (i <= n-2):

54 ab[ind(k,k-1)] = -1.

55 ab[ind(k,k-(n-2))] = -1.

56 ab[ind(k,k+1)] = -1.

57 ab[ind(k,k+n-2)] = -1.

58 else: # i == n-1

59 ab[ind(k,k-1)] = -1.

60 ab[ind(k,k-(n-2))] = -1.

61 ab[ind(k,k+n-2)] = -1.

62 else: # j == n-1

63 if (i == 2):

64 ab[ind(k,k-(n-2))] = -1.

65 ab[ind(k,k+1)] = -1.

66 elif (i <= n-2):

67 ab[ind(k,k-1)] = -1.

68 ab[ind(k,k-(n-2))] = -1.

69 ab[ind(k,k+1)] = -1.

70 else: # i == n-1

71 ab[ind(k,k-1)] = -1.

72 ab[ind(k,k-(n-2))] = -1.

74# resolve

75u = solve_banded((l,u), ab, b)

1.1.1 Exercícios

E. 1.1.1.

Considere o seguinte problema de Poisson⁴⁴4Siméon Denis Poisson, 1781 - 1840, matemático francês. Fonte: Wikipédia: Siméon Denis Poisson. unidimensional e com condições de contorno de Dirichlet não-homogêneas

	$\displaystyle-u^{\prime\prime}(x)=f(x),$		(1.39)
	$\displaystyle u(0)=1,$		(1.40)
	$\displaystyle u(1)=-1.$		(1.41)

para $x\in(0,1)$ . Assumindo a fonte $f(x)=\pi^{2}\cos(\pi x)$ . Aplique o método de diferenças finitas para computar uma aproximação para a solução do problema. Use diferenças finitas centrais para a segunda derivada e uma malha uniforme.

Dica: $u(x)=\cos(\pi x)$

E. 1.1.2.

Considere o seguinte problema de Poisson⁵⁵5Siméon Denis Poisson, 1781 - 1840, matemático francês. Fonte: Wikipédia: Siméon Denis Poisson. unidimensional

	$\displaystyle-u^{\prime\prime}(x)=f(x),$		(1.42)
	$\displaystyle u(0)=1,$		(1.43)
	$\displaystyle u^{\prime}(1)=0.$		(1.44)

Dica: $u(x)=\cos(\pi x)$

E. 1.1.3.

Considere o seguinte problema de valor de contorno

	$\displaystyle-u^{\prime\prime}(x)+u^{\prime}(x)=f(x),$		(1.45)
	$\displaystyle u(0)=0,$		(1.46)
	$\displaystyle u(1)=0.$		(1.47)

para $x\in(0,1)$ . Assumindo a fonte $f(x)=\pi^{2}\operatorname{sen}(\pi x)+\pi\cos(x)$ . Aplique o método de diferenças finitas para computar uma aproximação para a solução do problema. Use diferenças finitas centrais para as derivadas e uma malha uniforme.

Dica: $u(x)=\sin(\pi x)$

E. 1.1.4.

Considere o seguinte problema de valor de contorno

	$\displaystyle-u^{\prime\prime}(x)+au^{\prime}(x)=f(x),$		(1.48)
	$\displaystyle u(0)=0,$		(1.49)
	$\displaystyle u(1)=0.$		(1.50)

para $x\in(0,1)$ . Assumindo a fonte $f(x)=\operatorname{sen}(\pi x)$ , aplique o método de diferenças finitas para computar uma aproximação para a solução do problema. Use diferenças finitas centrais para as derivadas e uma malha uniforme. Faça simulações e estude os resultados para:

•

$a=1$
•

$a=0.1$
•

$a=-1$

E. 1.1.5.

Considere o seguinte problema de Poisson⁶⁶6Siméon Denis Poisson, 1781 - 1840, matemático francês. Fonte: Wikipédia: Siméon Denis Poisson. 2D com condições de contorno de Dirichlet

	$\displaystyle-\Delta u=0,\leavevmode\nobreak\ (x,y)\in(0,1)^{2},$		(1.51)
	$\displaystyle u(0,y)=0,\leavevmode\nobreak\ y\in[0,1],$		(1.52)
	$\displaystyle u(1,y)=0,\leavevmode\nobreak\ y\in[0,1],$		(1.53)
	$\displaystyle u(x,0)=\operatorname{sen}(\pi x),\leavevmode\nobreak\ x\in[0,1],$		(1.54)
	$\displaystyle u(x,1)=-\operatorname{sen}(\pi x),\leavevmode\nobreak\ x\in[0,1].$		(1.55)

Aplique o método de diferenças finitas para computar uma aproximação para a solução do problema. Use diferenças finitas centrais para as derivadas e uma malha uniforme.

Dica: $u(x,y)=\operatorname{sen}(\pi x)\cos(\pi y)$

E. 1.1.6.

Considere o seguinte problema de Poisson⁷⁷7Siméon Denis Poisson, 1781 - 1840, matemático francês. Fonte: Wikipédia: Siméon Denis Poisson. 2D com condições de contorno de Dirichlet

	$\displaystyle-\Delta u=8(y^{2}-2x+2x^{2}),\leavevmode\nobreak\ (x,y)\in(0,1)^{% 2},$		(1.56)
	$\displaystyle u(0,y)=0,\leavevmode\nobreak\ y\in[0,1],$		(1.57)
	$\displaystyle u(1,y)=0,\leavevmode\nobreak\ y\in[0,1],$		(1.58)
	$\displaystyle u(x,0)=0,\leavevmode\nobreak\ x\in[0,1],$		(1.59)
	$\displaystyle u(x,1)=8x(1-x),\leavevmode\nobreak\ x\in[0,1].$		(1.60)

Aplique o método de diferenças finitas para computar uma aproximação para a solução do problema. Use diferenças finitas centrais para as derivadas e uma malha uniforme.

Dica: $u(x,y)=8(x-x^{2})y^{2}$

E. 1.1.7.

Considere o seguinte problema de Poisson⁸⁸8Siméon Denis Poisson, 1781 - 1840, matemático francês. Fonte: Wikipédia: Siméon Denis Poisson. 2D com condições de contorno

	$\displaystyle-\Delta u=8(y^{2}-2x+2x^{2}),\leavevmode\nobreak\ (x,y)\in(0,1)^{% 2},$		(1.61)
	$\displaystyle u(0,y)=0,\leavevmode\nobreak\ y\in[0,1],$		(1.62)
	$\displaystyle u(1,y)=0,\leavevmode\nobreak\ y\in[0,1],$		(1.63)
	$\displaystyle u(x,0)=0,\leavevmode\nobreak\ x\in[0,1],$		(1.64)
	$\displaystyle u_{x}(x,1)=8(1-x),\leavevmode\nobreak\ x\in[0,1].$		(1.65)

Aplique o método de diferenças finitas para computar uma aproximação para a solução do problema. Use diferenças finitas centrais para as derivadas e uma malha uniforme. Na condição de Neumann, use uma fórmula de diferenças finitas para trás.