Matemática Numérica III

1 Sistemas Lineares 1.1 Matrizes bandas 1.3 Métodos iterativos básicos

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

1.2 Matrizes esparsas

Uma matriz é dita ser esparsa quando ela tem apenas poucos elementos não nulos. A ideia é que os elementos não nulos não precisam ser guardados na memória do computador, gerando um grande benefício na redução da demanda de armazenamento de dados. O desafio está no desenvolvimento de estruturas de dados para a alocação eficiente de tais matrizes, i.e. que sejam suficientemente adequadas para os métodos numéricos conhecidos.

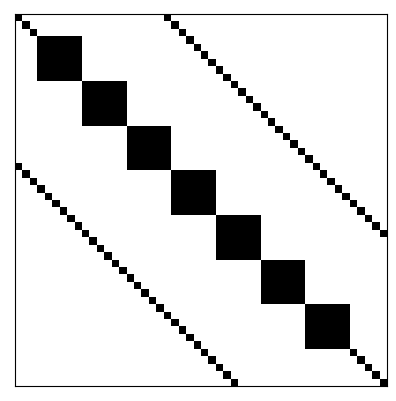
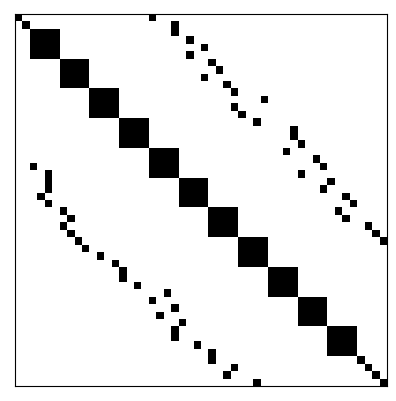
Refer to caption — Figura 1.3: Em cima: exemplo de uma matriz esparsa estruturada. Em baixo: exemplo de uma matriz esparsa não-estruturada.

Matrizes esparsas podem ser classificadas como estruturadas ou não-estruturadas. Uma matriz estruturada é aquela em que as entradas não-nulas formam um padrão regular. Por exemplo, estão dispostas em poucas diagonais ou formam blocos (submatrizes densas) ao longo de sua diagonal principal. No caso de não haver um padrão regular das entradas não-nulas, a matriz esparsa é dita ser não-estruturada. Consulte a Figura 1.3 para exemplos.

A esparsidade de uma matriz é a porcentagem de elementos nulos que ela tem, i.e. para uma matriz quadrada $n\times n$ tem-se que a esparsidade é

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}e:=\frac{n_{% \text{nulos}}}{n^{2}}\times 100\%.

(1.66)

Por exemplo, a matriz identidade de tamanho $n=100$ tem esparsidade

e=\frac{100^{2}-100}{100^{2}}\times 100\%=99\%.

(1.67)

1.2.1 Esquemas de armazenamento

A ideia é armazenar apenas os elementos não-nulos de uma matriz esparsa, de forma a economizar a demanda de armazenamento computacional. Cuidados devem ser tomados para que a estrutura de armazenamento utilizada seja adequada para a computação das operações matriciais mais comuns.

Formato COO

O formato COO (do inglês, COOrdinate format) é o esquema de armazenamento simples de matrizes esparsas. As estrutura de dados consiste em três arranjos:

1.

um arranjo contendo as entradas não-nulas da matriz;
2.

um arranjo contendo seus índices de linha;
3.

um arranjo contendo seus índices de coluna.

O método scipy.sparse.coo_array permite a alocação de matrizes no formato COO.

Exemplo 1.2.1.

O seguinte código armazena a matriz

A=\begin{bmatrix}2.&0.&1.&0.\\ 0.&3.&2.&-1.\\ 0&-1&-2.&0.\\ 0&0&0&1.\end{bmatrix}

(1.68)

no formato COO.

⬇

1from scipy.sparse import coo_array

3data = [2.,1.,3.,2.,-1.,-1.,-2.,1.]

4row = [0,0,1,1,1,2,2,3]

5col = [0,2,1,2,3,1,2,3]

6Acoo = coo_array((data, (row, col)), shape=(4,4))

7print("Acoo = \n", Acoo)

8print("A = \n", Acoo.toarray())

Vantagens do formato COO

•

Permite a entrada de dados duplicados (simplicidade).
•

Conversão rápida para os formatos CSR e CSC.

Desavantagens do formato COO - não suporta diretamente:

•

operações aritméticas.
•

fatiamento.

Observação 1.2.1.(Entradas duplicadas)

O formato COO permite a entrada duplicada de elementos. Nestes casos, na alocação da coo_array, os elementos duplicados são somados. Por exemplo, considere o seguinte código.

⬇

1from scipy.sparse import coo_array

3data = [2.,3.,2.,1.]

4row = [0,1,1,0]

5col = [0,0,1,0]

6Acoo = coo_array((data, (row, col)), shape=(2,2))

7print("Acoo = \n", Acoo)

8print("A = \n", Acoo.toarray())

Exemplo 1.2.2.(Equação de Poisson 2D)

Consideremos a aproximação pelo método de diferenças finitas do problema de Poisson⁹⁹endnote: ⁹Siméon Denis Poisson, 1781 - 1840, matemático francês. Fonte: Wikipédia:Siméon Denis Poisson. 2D trabalhado no Exemplo 1.1.3. O seguinte código, faz a alocação da matriz do problema discreto no formato COO. Ao final, o sistema é resolvido usando a função scipy.sparse.linalg.spsolve.

Código 3: poisson2d_coo.py

⬇

1import numpy as np

2from scipy.sparse import coo_array

3from scipy.sparse.linalg import spsolve

5# malha

6n = 11

7h = 1/(n-1)

9xx = np.linspace(0, 1, n)

10yy = np.linspace(0, 1, n)

12# fonte

13def f(x,y):

14 return 2 * np.pi**2 * np.sin(np.pi*x) * np.sin(np.pi*y)

16# sistema discreto

17data = []

18row = []

19col = []

20def add(i,j,v):

21 data.append(v)

22 row.append(i)

23 col.append(j)

25## vetor b

26b = np.empty((n-2)**2)

28## montagem

29for j in np.arange(2,n):

30 for i in np.arange(2,n):

32 # enumeração dos nodos computacionais

33 k = i-2 + (j-2)*(n-2)

35 # vetor b

36 b[k] = h**2 * f(xx[i-1], yy[j-1])

38 # matriz ab

39 add(k,k,4.)

41 if (j == 2):

42 if (i == 2):

43 add(k,k+1,-1.)

44 add(k,k+n-2,-1.)

45 elif (i <= n-2):

46 add(k,k-1,-1.)

47 add(k,k+1,-1.)

48 add(k,k+n-2,-1.)

49 else: # i == n-1

50 add(k,k-1,-1.)

51 add(k,k+n-2,-1.)

52 elif (j <= n-2):

53 if (i == 2):

54 add(k,k-(n-2),-1.)

55 add(k,k+1,-1.)

56 add(k,k+n-2,-1.)

57 elif (i <= n-2):

58 add(k,k-1,-1.)

59 add(k,k-(n-2),-1.)

60 add(k,k+1,-1.)

61 add(k,k+n-2,-1.)

62 else: # i == n-1

63 add(k,k-1,-1.)

64 add(k,k-(n-2),-1.)

65 add(k,k+n-2,-1.)

66 else: # j == n-1

67 if (i == 2):

68 add(k,k-(n-2),-1.)

69 add(k,k+1,-1.)

70 elif (i <= n-2):

71 add(k,k-1,-1.)

72 add(k,k-(n-2),-1.)

73 add(k,k+1,-1.)

74 else: # i == n-1

75 add(k,k-1,-1.)

76 add(k,k-(n-2),-1.)

78acoo = coo_array((data, (row, col)), shape=((n-2)**2,(n-2)**2))

80# resolve

81u = spsolve(acoo, b)

Formato CSR

O formato CSR (do inglês, Compressed Sparse Row) é uma variação do COO que busca diminuir a alocação de dados repetidos. Assim como o COO, o formato conta com três arranjos $d$ , $c$ , $p$ :

•

$d$ é o arranjo contendo os elementos não-nulos da matriz, ordenados por linhas (i.e., da esquerda para direita, de cima para baixo);
•

$c$ é o arranjo contendo o índice das colunas das entradas não-nulas da matriz (como no formato COO);
•

$p$ é um arranjo cujos elementos são a posição no arranjo $c$ em que cada linha da matriz começa a ser representada. O número de elementos de $i$ -ésima linha da matriz dado por $p_{j+1}-p_{j}$ .

O método scipy.sparse.csr_array permite a alocação de matrizes no formato CSR.

Exemplo 1.2.3.

No Exemplo 1.2.1, alocamos a matriz

A=\begin{bmatrix}2.&0.&1.&0.\\ 0.&3.&2.&-1.\\ 0&-1&-2.&0.\\ 0&0&0&1.\end{bmatrix}

(1.69)

no formato COO. Aqui, vamos converter a alocação para o formato CSR e, então, verificar seus atributos.

⬇

1from scipy.sparse import csr_array

2Acsr = Acoo.tocsr()

3print(f'd = {Acsr.data}')

4print(f'c = {Acsr.indices}')

5print(f'p = {Acsr.indptr}')

d = [ 2.  1.  3.  2. -1. -1. -2.  1.]
c = [0 2 1 2 3 1 2 3]
p = [0 2 5 7 8]

Por exemplo, o elemento p[i=2] = 5 aponta para o c[k=5] = j = 1, o que fornece A[i=2,j=1] = d[k] = -1.. Verifique!

Vantagens do formato CSR

•

operações aritméticas eficientes;
•

fatiamento por linhas eficiente;
•

multiplicação matriz vetor eficiente.

Desvantagens do formato CSR

•

fatiamento por colunas não eficiente;
•

custo elevado de realocação com alteração da esparsidade da matriz.

Formato CSC

O formato CSC (do inglês, Compressed Sparse Column) é uma variação análoga do CSR, mas para armazenamento por colunas. O formato conta com três arranjos $d$ , $l$ , $p$ :

•

$d$ é o arranjo contendo os elementos não-nulos da matriz, ordenados por colunas (i.e., de cima para baixo, da esquerda para direita);
•

$l$ é o arranjo contendo o índice das linhas das entradas não-nulas da matriz;
•

$p$ é um arranjo cujos elementos são a posição no arranjo $l$ em que cada coluna da matriz começa a ser representada. O número de elementos de $j$ -ésima coluna da matriz dado por $p_{j+1}-p_{j}$ .

O método scipy.sparse.csc_array permite a alocação de matrizes no formato CSC.

Exemplo 1.2.4.

No Exemplo 1.2.1, alocamos a matriz

A=\begin{bmatrix}2.&0.&1.&0.\\ 0.&3.&2.&-1.\\ 0&-1&-2.&0.\\ 0&0&0&1.\end{bmatrix}

(1.70)

no formato COO. Aqui, vamos converter a alocação para o formato CSC e, então, verificar seus atributos.

⬇

1 from scipy.sparse import csc_array

2 Acsc = Acoo.tocsc()

3 l = Acsc.indices

4 p = Acsc.indptr

5 print(f'd = {Acsc.date}')

6 print(f'l = {Acsc.indices}')

7 print(f'p = {Acsc.indptr}')

  d = [2.  3. -1.  1.  2. -2. -1.  1.]
  l = [0 1 2 0 1 2 1 3]
  p = [0 1 3 6 8]

Assim sendo, o elemento p[j=2] = 3 aponta para o l[k=3] = 0, o que informa que A[i=0,j=2]=d[k]=1.. Verifique!

Vantagens do formato CSC

•

fatiamento por colunas eficiente;
•

operações aritméticas eficientes;
•

multiplicação matriz vetor eficiente¹⁰¹⁰endnote: ¹⁰CSR é mais eficiente em muitos casos..

Desvantagens do formato CSC

•

fatiamento por linhas não eficiente;
•

custo elevado de realocação com alteração da esparsidade da matriz.

Observação 1.2.2.

Além dos formatos COO, CSR e CSC, exitem ainda vários outros que podem empregados e que são mais eficientes em determinadas aplicações. Recomendamos a leitura de [9, Seção 3.4] e da documentação do scipy.sparse.

Exercícios

E. 1.2.1.

Considere o seguinte problema de valor de contorno

	$\displaystyle-u^{\prime\prime}(x)+u^{\prime}(x)=f(x),$		(1.71)
	$\displaystyle u(0)=0,$		(1.72)
	$\displaystyle u(1)=0.$		(1.73)

para $x\in(0,1)$ . Assumindo a fonte $f(x)=\pi^{2}\operatorname{sen}(\pi x)+\pi\cos(x)$ . Aplique o método de diferenças finitas para computar uma aproximação para a solução do problema. Use diferenças finitas centrais para as derivadas e uma malha uniforme. Use o formato COO para armazenar a matriz do problema discreto $A\boldsymbol{u}=\boldsymbol{b}$ . Então, compute sua solução com o método scipy.sparse.linalg.spsolve para matrizes em formato

a)

CSR
b)

CSC

Dica: $u(x)=\sin(\pi x)$

E. 1.2.2.

Armazene a matriz

A=\begin{bmatrix}2&0&-1&0\\ 0&3&0&-2\\ 0&-1&-2&0\\ 1&0&0&1\end{bmatrix}

(1.74)

em cada um dos seguintes formatos

a)

COO
b)

CSR
c)

CSC

e, então, adicione o valor $7$ ao elemento da segunda linha e terceira coluna.

⬇

1from scipy.sparse import coo_array

3# matriz original

4data = [2,-1,3,-2,-1,-2,1,1]

5row = [0,0,1,1,2,2,3,3]

6col = [0,2,1,3,1,2,0,3]

7Acoo = coo_array((data, (row, col)), shape=(4,4))

9# add elemnto não-nulo

10data.append(7)

11 row.append(1)

12col.append(2)

13Acoo = coo_array((data, (row, col)), shape=(4,4))

14print("Acoo = \n", Acoo.toarray())

E. 1.2.3.

Considere o seguinte sistema linear

	$\displaystyle 2x_{1}+x_{2}=1$		(1.75)
	$\displaystyle 3x_{2}+2x_{3}-x_{4}=-1$		(1.76)
	$\displaystyle-x_{2}-2x_{3}=1$		(1.77)
	$\displaystyle x_{4}=-2$		(1.78)

Armazene sua matriz de coeficientes $A$ em formato CSC e compute sua fatoração LU. Então, resolva o sistema usando a fatoração obtida.

Dica: verifique seu resultados com o método scipy.sparse.linalg.splu.

	$\displaystyle A=LU$
	$\displaystyle L=\begin{bmatrix}1&0&0&0\\ 0&1&0&0\\ 0&-\frac{1}{3}&1&0\\ 0&0&0&1\end{bmatrix}$
	$\displaystyle U=\begin{bmatrix}2&0&1&0\\ 0&3&2&0\\ 0&0&-\frac{4}{3}&0\\ 0&0&0&1\end{bmatrix}$
	$\displaystyle x=(1,-1,0,-2)$

E. 1.2.4.

Considere a seguinte equação diferencial parcial de difusão-advecção com condições de contorno de Dirichlet homogêneas

-\Delta u+\boldsymbol{a}\cdot\nabla u=8(x-x^{2})(y-y^{2}),\leavevmode\nobreak% \ (x,y)\in(0,1)^{2}.

(1.79)

Aplique o método de diferenças finitas para obter um problema discreto $A\boldsymbol{u}=\boldsymbol{b}$ que aproxime a solução. Use os formatos de armazenamento de matrizes esparsas adequados e compute a solução aproximada. Estude cada um dos seguintes casos:

a)

$\boldsymbol{a}=(1,0)$
b)

$\boldsymbol{a}=(0,-1)$
c)

$\boldsymbol{a}=(1,-1)$

Dica: use fórmulas de diferenças finitas progressiva ou regressiva para aproximar $\nabla u=(u_{x},u_{y})$ de acordo com o vetor $\boldsymbol{a}$ .

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Política de uso de dados

Política de uso de dados

Matemática Numérica III

1.2 Matrizes esparsas

1.2.1 Esquemas de armazenamento

Formato COO

Exemplo 1.2.1.

Observação 1.2.1.(Entradas duplicadas)

Exemplo 1.2.2.(Equação de Poisson 2D)

Formato CSR

Exemplo 1.2.3.

Formato CSC

Exemplo 1.2.4.

Observação 1.2.2.

Exercícios

E. 1.2.1.

E. 1.2.2.

E. 1.2.3.

E. 1.2.4.

Envie seu comentário