Matemática Numérica II

4 Problema de Valor Inicial 4 Problema de Valor Inicial 4.2 Métodos de Taylor de Alta Ordem

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

4.1 Método de Euler

Dado um Problema de Valor Inicial (PVI)


	$\displaystyle y^{\prime}(t)=f(t,y(t)),\quad t>t_{0},$		(4.3a)
	$\displaystyle y(t_{0})=y_{0},$		(4.3b)

temos que $f(t,y)$ é a derivada da solução $y(t)$ no tempo $t$ . Então, aproximando a derivada pela razão fundamental de passo $h>0$

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}y^{\prime}(t)% \approx\frac{y(t+h)-y(t)}{h},

(4.4)

obtemos

	$\displaystyle\frac{y(t+h)-y(t)}{h}\approx f(t,y)$		(4.5)
	$\displaystyle\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% y(t+h)\approx y(t)+hf(t,y(t)).$		(4.6)

Isto nos motiva a iteração do Método de Euler⁸⁸endnote: ⁸Leonhard Paul Euler, 1707-1783, matemático e físico suíço. Fonte: Wikipédia: Ronald Fisher.


	$\displaystyle y^{(0)}=y_{0},$		(4.7a)
	$\displaystyle y^{(k+1)}=y^{(k)}+hf(t^{(k)},y^{(k)}),$		(4.7b)

com $k=0,1,2,\dotsc,n$ , $y^{(k)}\approx y\left(t^{(k)}\right)$ , $t^{(k)}=t_{0}+kh$ e passo $h>0$ .

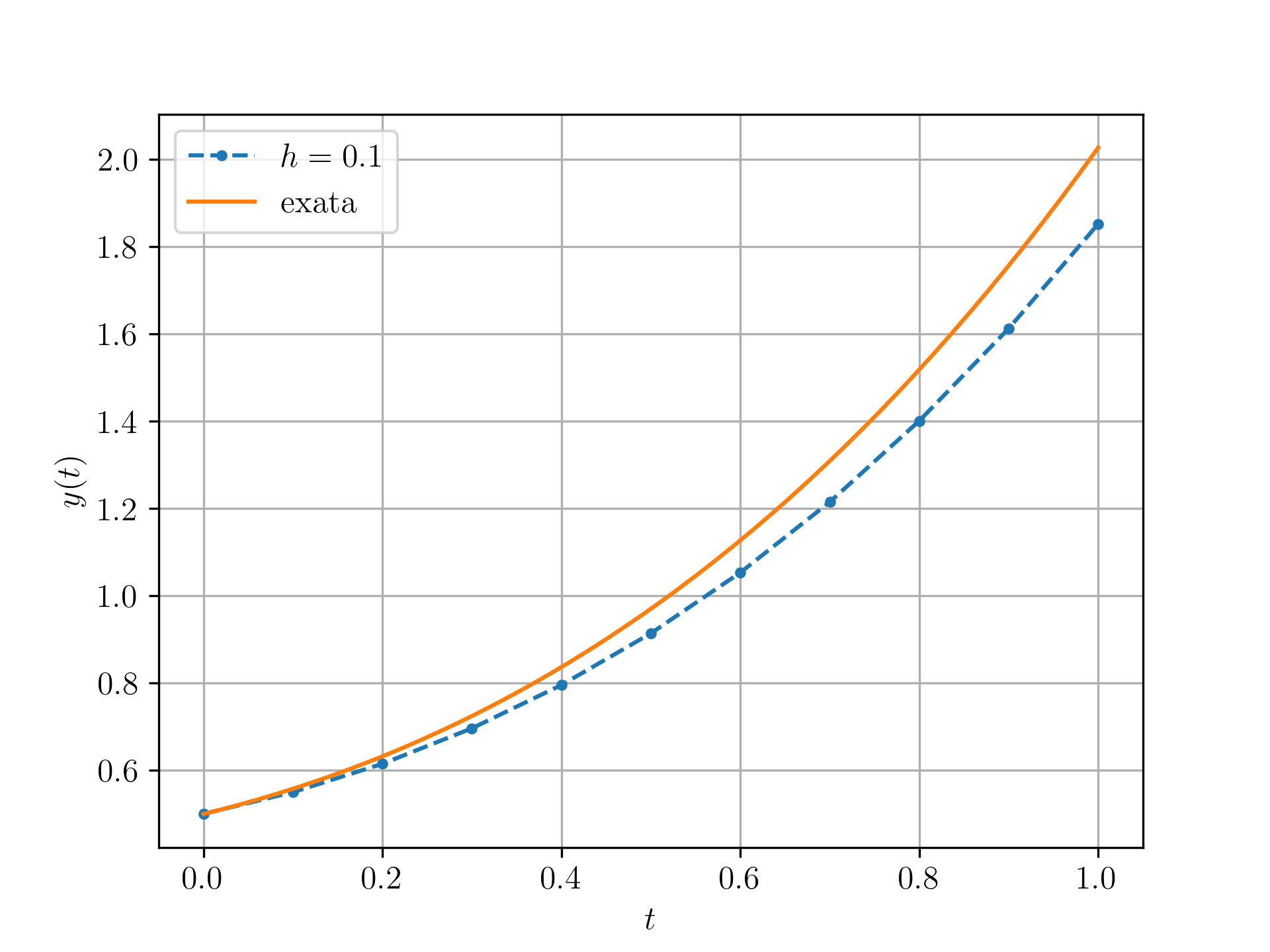
Exemplo 4.1.1.

Consideramos o seguinte problema de valor inicial


	$\displaystyle y^{\prime}-y=\operatorname{sen}(t),0<t<1,$		(4.8a)
	$\displaystyle y(0)=\frac{1}{2}.$		(4.8b)

Sua solução analítica é

y(t)=e^{t}-\frac{1}{2}\operatorname{sen}(t)-\frac{1}{2}\cos(t).

(4.9)

Para computarmos a solução pelo Método de Euler, reescrevemos o problema da seguinte forma


	$\displaystyle y^{\prime}=y+\operatorname{sen}(t),0<t<1,$		(4.10a)
	$\displaystyle y(0)=\frac{1}{2},$		(4.10b)

donde identificamos $f(t,y):=y+\operatorname{sen}(t)$ , $t_{0}=0$ e $y_{0}=1/2$ .

Tabela 4.1: Resultados obtidos para o problema do Exemplo 4.1.1 com

h=1\mathrm{e}\!-\!1

$k$	$t^{(k)}$	$y^{(k)}$	$y\left(t^{(k)}\right)$
$0$	$0.0$	$5.00\mathrm{e}\!-\!1$	$5.00\mathrm{e}\!-\!1$
$1$	$0.1$	$5.50\mathrm{e}\!-\!1$	$5.58\mathrm{e}\!-\!1$
$2$	$0.2$	$6.15\mathrm{e}\!-\!1$	$6.32\mathrm{e}\!-\!1$
$3$	$0.3$	$6.96\mathrm{e}\!-\!1$	$7.24\mathrm{e}\!-\!1$
$4$	$0.4$	$7.96\mathrm{e}\!-\!1$	$8.37\mathrm{e}\!-\!1$
$5$	$0.5$	$9.14\mathrm{e}\!-\!1$	$9.70\mathrm{e}\!-\!1$
$6$	$0.6$	$1.05\mathrm{e}\!+\!0$	$1.13\mathrm{e}\!+\!0$
$7$	$0.7$	$1.22\mathrm{e}\!+\!0$	$1.31\mathrm{e}\!+\!0$
$8$	$0.8$	$1.40\mathrm{e}\!+\!0$	$1.52\mathrm{e}\!+\!0$
$9$	$0.9$	$1.61\mathrm{e}\!+\!0$	$1.76\mathrm{e}\!+\!0$
$10$	$1.0$	$1.85\mathrm{e}\!+\!0$	$2.03\mathrm{e}\!+\!0$

Refer to caption — Figura 4.1: Esboço das soluções numérica (pontos) e analítica (linha) para o problema do Exemplo 4.1.1.

Código 8: euler.py

⬇

1def euler(f, t0, y0, h, n):

2 t = np.empty(n+1)

3 t[0] = t0

4 y = np.empty(n+1)

5 y[0] = y0

6 for k in range(n):

7 t[k+1] = t[k] + h

8 y[k+1] = y[k] + h*f(t[k], y[k])

9 return t, y

4.1.1 Análise Numérica

O Método de Euler com passo $h$ aplicado ao problema de valor inicial (4.3), pode ser escrito da seguinte forma


	$\displaystyle\tilde{y}(t^{(0)};h)=y_{0},$		(4.11a)
	$\displaystyle\tilde{y}(t^{(k+1)};h)=\tilde{y}(t^{(k)};h)+h\Phi(t^{(k)},\tilde{% y}(t^{(k)});h),$		(4.11b)

onde $\tilde{y}(t^{(k)})$ representa a aproximação da solução exata $y$ no tempo $t^{(k)}=t_{0}+kh$ , $k=0,1,2,\ldots$ . Métodos que podem ser escritos dessa forma, são chamados de Métodos de Passo Simples (ou único). No caso específico do Método de Euler, temos

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\Phi(t,y;h):=% f(t,y(t)).

(4.12)

Consistência

Agora, considerando a solução exata $y$ de (4.3), introduzimos

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\Delta(t,y;h)% :=\left\{\begin{array}[]{ll}\displaystyle\frac{y(t+h)-y(t)}{h}&,h\neq 0,\\ f(t,y(t))&,h=0.\end{array}\right.

(4.13)

Com isso, vamos analisar o chamado erro de discretização local

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\tau(t,y;h):=% \Delta(t,y;h)-\Phi(t,y;h),

(4.14)

que estabelece uma medida quantitativa com que a solução exata $y(t)$ no tempo $t+h$ satisfaz a iteração do método de passo simples.

Definição 4.1.1.

(Consistência.) Um método de passo simples é dito ser consistente quando

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\lim_{h\to 0}% \tau(t,y;h)=0,

(4.15)

ou, equivalentemente, quando

\lim_{h\to 0}\Phi(t,y;h)=f(t,y).

(4.16)

Observação 4.1.1.

(Consistência do Método de Euler.) Da Definição 4.1.1, temos que o Método de Euler é consistente. De fato, temos

	$\displaystyle\lim_{h\to 0}\tau(t,y;h)=\lim_{h\to 0}\left(\Delta(t,y;h)-\Phi(t,% y;h)\right)$		(4.17)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\left(\frac{y(t+h)-y(t)}{h}-f\left(t,y(% t)\right)\right)$		(4.18)
	$\displaystyle\text{}\quad=y^{\prime}(t)-f\left(t,y(t)\right)=0.$		(4.19)

A ordem do erro de discretização local de um método de passo simples é dita ser $p$ , quando

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\tau(t,y;h)=O% (h^{p}),

(4.20)

ou seja, quando

\lim_{h\to 0}\frac{\tau(t,y;h)}{h^{p}}=C,

(4.21)

para alguma constante $C$ .

Para determinarmos a ordem do Método de Euler, tomamos a expansão em série de Taylor⁹⁹endnote: ⁹Brook Taylor, 1685 - 1731, matemático britânico. Fonte: Wikipédia:Brook Taylor. da solução exata $y(t)$ em torno de $t$ , i.e.

y(t+h)=y(t)+hy^{\prime}(t)+\frac{h^{2}}{2}y^{\prime\prime}(t)+\frac{h^{3}}{6}y% ^{\prime\prime\prime}(t+\theta h),

(4.22)

para algum $0<\theta<1$ . Como $y^{\prime}(t)=f(t,y(t))$ , temos

	$\displaystyle y^{\prime\prime}(t)=\frac{d}{dt}f(t,y(t))$		(4.23)
	$\displaystyle\text{}\quad=f_{t}(t,y)+f_{y}(t,y)y^{\prime}$		(4.24)
	$\displaystyle\text{}\quad=f_{t}(t,y)+f_{y}(t,y)f(t,y).$		(4.25)

Então, rearranjando os termos em (4.22), obtemos

\Delta(t,y;h)=f(t,y(t))+\frac{h}{2}[f_{t}(t,y)+f_{y}(t,y)f(t,y)]+O(h^{2}).

(4.26)

Portanto, para o Método de Euler temos

	$\displaystyle\tau(t,y;h):=\Delta(t,y;h)-\Phi(t,y;h)$		(4.27)
	$\displaystyle\text{}\quad=\Delta(t,y;h)-f(t,y)$		(4.28)
	$\displaystyle\text{}\quad=\frac{h}{2}[f_{t}(t,y)+f_{y}(t,y)f(t,y)]+O(h^{2})$		(4.29)
	$\displaystyle\text{}\quad=O(h).$		(4.30)

Isto mostra que o Método de Euler é de ordem $1$ .

Convergência

A análise acima trata apenas da consistência do Método de Euler. Para analisarmos a convergência de métodos de passo simples, definimos o erro de discretização global

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}e(t;h_{n}):=% \tilde{y}(t;h_{n})-y(t),

(4.31)

onde $\tilde{y}(t;h_{n})\approx y(t)$ para $h_{n}:=(t-t_{0})/n$ . Dizemos que o método é convergente quando

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\lim_{n\to% \infty}e(t;h_{n})=0.

(4.32)

Ainda, dizemos que o método tem erro de discretização global de ordem $p$ quando

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}e(t;h_{n})=O(% h_{n}^{p})

(4.33)

para todo $t\in[t_{0},t_{f}]$ , $t_{f}>t_{0}$ .

Lema 4.1.1.

([8, Cap. 7, Seção 7.2]) Se a sequência $\left(\xi^{(k)}\right)_{k\in\mathbb{R}}$ satisfaz a estimativa

\left|\xi^{(k+1)}\right|\leq(1+\delta)\left|\xi^{(k)}\right|+B,

(4.34)

para dados $\delta>0$ e $B\geq 0$ , $k=0,1,2,\ldots$ , então

\left|\xi^{(n)}\right|\leq e^{n\delta}\left|\xi^{(0)}\right|+\frac{e^{n\delta}% -1}{\delta}B.

(4.35)

Demonstração.

De forma iterativa, temos

	$\displaystyle\left\|\xi^{(1)}\right\|\leq(1+\delta)\left\|\xi^{(0)}\right\|+B$		(4.36)
	$\displaystyle\left\|\xi^{(2)}\right\|\leq(1+\delta)\left\|\xi^{(1)}\right\|+B$		(4.37)
	$\displaystyle\text{}\quad=(1+\delta)^{2}\left\|\xi^{(0)}\right\|+(1+\delta)B+B$		(4.38)
	$\displaystyle\text{}\qquad\vdots$		(4.39)
	$\displaystyle\left\|\xi^{(k)}\right\|\leq(1+\delta)^{k}\left\|\xi^{(0)}\right\|+B% \sum_{k=0}^{k-1}(1+\delta)^{k}$		(4.40)
	$\displaystyle\text{}\quad=(1+\delta)^{k}\left\|\xi^{(0)}\right\|+B\frac{(1+% \delta)^{k}-1}{\delta}.$		(4.41)

Observando que $0<1+\delta\leq e^{\delta}$ para $\delta>-1$ , concluímos que

\left|\xi^{(k)}\right|\leq e^{k\delta}\left|\xi^{(0)}\right|+\frac{e^{k\delta}% -1}{\delta}B.

(4.42)

∎

Teorema 4.1.1.

(Estimativa do Error Global.) Considere o PVI (4.3), para $t_{0}=a$ , $y_{0}\in\mathbb{R}$ . Suponha que $f$ é Lipschitz contínua em $y$

|f(t,y)-f(t,z)|\leq L|y-z|,

(4.43)

para todo $(t,y)\in[a,b]\times\mathbb{R}$ e que exista $M>0$ tal que

|y^{\prime\prime}(t)|\leq M,

(4.44)

para todo $t\in[a,b]$ . Então, as iteradas do Método de Euler $y^{(k)}\approx y\left(t^{(k)}\right)$ , $t^{(k)}=t_{0}+kh$ , $h>(b-a)/n$ , $k=0,1,2,\dotsc,n+1$ , satisfazem a seguinte estimativa do erro de discretização global

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\left|y^{(k)}% -y\left(t^{(k)}\right)\right|\leq\frac{hM}{2L}\left[e^{L\left(t^{(k)}-t_{0}% \right)}-1\right].

(4.45)

Demonstração.

Para $k=0$ o resultado é imediato. Agora, usamos o polinômio de Taylor

y\left(t^{(k+1)}\right)=y\left(t^{(k)}\right)+hf\left(t^{(k)},y\left(t^{(k)}% \right)\right)+\frac{h^{2}}{2}y^{\prime\prime}\left(\xi^{(k)}\right),

(4.46)

onde $t^{(k)}\leq\xi^{(k)}\leq t^{(k+1)}$ , $k=0,1,2,\ldots,n$ . Já, as iteradas de Euler são

y^{(k+1)}=y^{(k)}+hf\left(t^{(k)},y^{(k)}\right).

(4.47)

Subtraindo esses equações, obtemos

		$\displaystyle y^{(k+1)}-y\left(t^{(k+1)}\right)=y^{(k)}-y\left(t^{(k)}\right)$		(4.48)
		$\displaystyle\text{}\quad+h\left[f\left(t^{(k)},y^{(k)}\right)-f\left(t^{(k)},% y\left(t^{(k)}\right)\right)\right]-\frac{h^{2}}{2}y^{\prime\prime}\left(\xi^{% (k)}\right)$		(4.48)

Da hipótese de $f$ Lipschitz, temos

		$\displaystyle\left\|y^{(k+1)}-y\left(t^{(k+1)}\right)\right\|\leq\left\|y^{(k)}-y% \left(t^{(k)}\right)\right\|$		(4.49)
		$\displaystyle\text{}\quad+hL\left\|y^{(k)}-y\left(t^{(k)}\right)\right\|+\frac{h% ^{2}}{2}\left\|y^{\prime\prime}\left(\xi^{(k)}\right)\right\|$		(4.49)

Ou, ainda,

\left|y^{(k+1)}-y\left(t^{(k+1)}\right)\right|\leq(1+hL)\left|y^{(k)}-y\left(t% ^{(k)}\right)\right|+\frac{h^{2}M}{2}.

(4.50)

Do Lema 4.1.1, temos

\left|y^{(k+1)}-y\left(t^{(k+1)}\right)\right|\leq\frac{h^{2}M}{2}\frac{e^{khL% }-1}{hL},

(4.51)

donde segue a estimativa do erro global (4.45). ∎

Observação 4.1.2.

(Convergência.) Do Teorema 4.1.1, a ordem do erro de discretização global de um método de passo simples é igual a sua ordem do erro de discretização local. Portanto, o Método de Euler é convergente e é de ordem $1$ .

Exemplo 4.1.2.

Consideramos o seguinte problema de valor inicial


	$\displaystyle y^{\prime}=y+1,0<t<1,$		(4.52a)
	$\displaystyle y(0)=0.$		(4.52b)

Na Tabela 4.2, temos as aproximações $\tilde{y}(1)$ de $y(1)$ computadas pelo Método de Euler com diferentes passos $h$ . A solução analítica deste problema é $y(t)=e^{t}-1$ .

Tabela 4.2: Resultados referentes ao Exemplo 4.1.2.

$h$	$\tilde{y}(1)$	$\|\tilde{y}(1)-y(1)\|$
$10^{-1}$	$1.59374$	$1.2\mathrm{e}\!-\!1$
$10^{-2}$	$1.70481$	$1.3\mathrm{e}\!-\!2$
$10^{-3}$	$1.71692$	$1.4\mathrm{e}\!-\!3$
$10^{-5}$	$1.71827$	$1.4\mathrm{e}\!-\!5$
$10^{-7}$	$1.71828$	$1.4\mathrm{e}\!-\!7$
$10^{-9}$	$1.71828$	$1.4\mathrm{e}\!-\!9$

Erros de Arredondamento

O Teorema 4.1.1 não leva em consideração os erros de arredondamento. Levando em conta esses erros, a iteração do Método de Euler tem a forma


	$\displaystyle\tilde{y}^{(0)}=y_{0}+\delta^{(k)},$		(4.53a)
	$\displaystyle\tilde{y}^{(k+1)}=\tilde{y}^{(k)}+hf\left(t^{(k)},\tilde{y}^{(k)}% \right)+\delta^{(k+1)},$		(4.53b)

onde $\delta^{(k)}$ é o erro devido a arredondamentos na $k$ -ésima iterada, $t^{(k)}=t_{0}+hk$ , $k=0,1,2,\dotsc,n$ . Assumindo as hipóteses do Teorema 4.1.1, podemos mostrar a seguinte estimativa de erro global

		$\displaystyle\left\|\tilde{y}^{(k+1)}-y\left(t^{(k+1)}\right)\right\|\leq\frac{1% }{L}\left(\frac{hM}{2}+\frac{\delta}{h}\right)\left[e^{L\left(t^{(k)}-t_{0}% \right)}-1\right]$		(4.54)
		$\displaystyle\text{}\quad+\|\delta_{0}\|e^{L\left(t^{(k)}-t_{0}\right)},$		(4.54)

para $\delta^{(k)}<\delta$ , $k=0,1,2,\dotsc,n$ .

4.1.2 Sistemas de Equações

Seja um sistema de EDOs¹⁰¹⁰endnote: ¹⁰Equações Diferenciais Ordinárias com valor iniciais


	$\displaystyle\boldsymbol{y}^{\prime}=\boldsymbol{f}(t,\boldsymbol{y}),t_{0}<t% \leq t_{f},$		(4.55a)
	$\displaystyle\boldsymbol{y}(t_{0})=\boldsymbol{y}_{0},$		(4.55b)

com dada $\boldsymbol{f}:(t,\boldsymbol{y})\in[t_{0},t_{f}]\times\mathbb{R}^{m}\mapsto% \mathbb{R}^{m}$ , dados valores iniciais $\boldsymbol{y}_{0}\in\mathbb{R}^{m}$ e incógnita $\boldsymbol{y}:t\in[t_{0},t_{f}]\mapsto\mathbb{R}^{m}$ , $n\geq 1$ .

Do ponto de vista algorítmico, a iteração do Método de Euler é diretamente estendida para sistemas:

		$\displaystyle\boldsymbol{y}^{(0)}=\boldsymbol{y}_{0},$		(4.56)
		$\displaystyle\boldsymbol{y}^{(k+1)}=\boldsymbol{y}^{(k)}+h\boldsymbol{f}\left(% t^{(k)},\boldsymbol{y}^{(k)}\right),$		(4.56)

para $\boldsymbol{y}^{(k)}\approx\boldsymbol{y}\left(t^{(k)}\right)$ , $t^{(k)}=t_{0}+kh$ , $h=(t_{f}-t_{0})/n$ , $k=0,1,2,\dotsc,n$ .

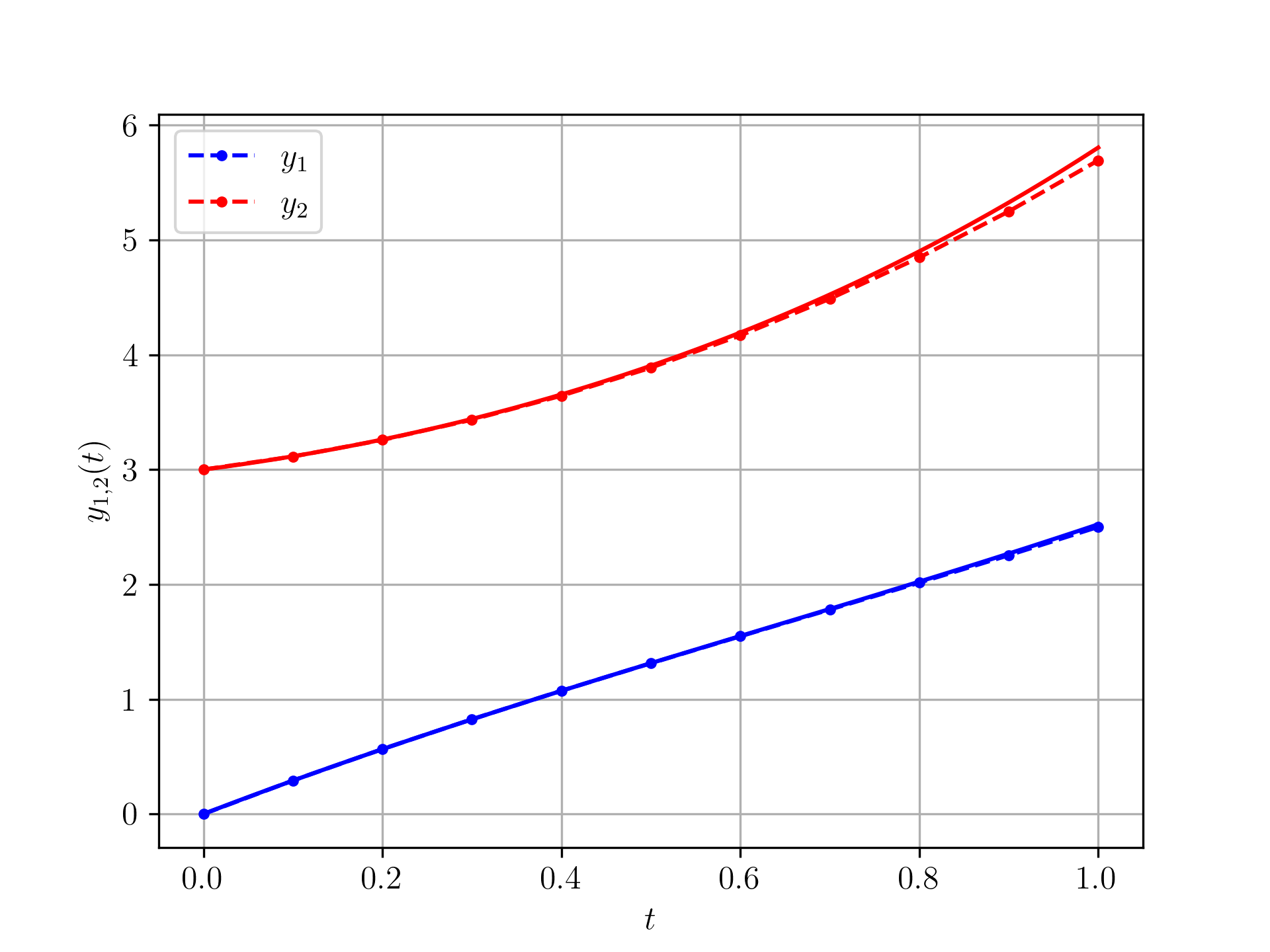
Exemplo 4.1.3.

Consideramos o sistema de EDOs


	$\displaystyle y_{1}^{\prime}=-y_{1}+y_{2}-e^{-t}-\operatorname{sen}(t)+\cos(t),$		(4.57a)
	$\displaystyle y_{2}^{\prime}=2y_{1}+3y_{2}-6e^{t}-2\cos(t),$		(4.57b)

para $0<t\leq 1$ com condições iniciais


	$\displaystyle y_{1}(0)=0,$		(4.58a)
	$\displaystyle y_{2}(0)=3.$		(4.58b)

Este sistema tem solução analítica


	$\displaystyle y_{1}(t)=e^{t}-2e^{-t}+\cos(t),$		(4.59a)
	$\displaystyle y_{2}(t)=2e^{t}+e^{-t}.$		(4.59b)

Podemos reescrevê-lo na forma vetorial


	$\displaystyle\underbrace{\begin{bmatrix}y_{1}^{\prime}\\ y_{2}^{\prime}\end{bmatrix}}_{\boldsymbol{y^{\prime}}(t)}=\underbrace{\begin{% bmatrix}-y_{1}+y_{2}+e^{-t}-\operatorname{sen}(t)+\cos(t)\\ 2y_{1}+3y_{2}-6e^{t}-2\cos(t)\end{bmatrix}}_{\boldsymbol{f}(t,\boldsymbol{y})}% ,0<t\leq t_{f}$		(4.60a)
	$\displaystyle\underbrace{\begin{bmatrix}y_{1}(0)\\ y_{2}(0)\end{bmatrix}}_{\boldsymbol{y}(0)}=\underbrace{\begin{bmatrix}0\\ 3\end{bmatrix}}_{\boldsymbol{y}_{0}}$		(4.60b)

Usando o Método de Euler com $h=10^{-2}$ obtemos as soluções mostradas na figura abaixo.

⬇

1import numpy as np

3def euler(f, t0, y0, h, n):

4 t = np.empty(n+1)

5 m = y0.size

6 y = np.empty((n+1, m))

8 t[0] = t0

9 y[0] = y0

11 for k in range(n):

12 t[k+1] = t[k] + h

13 y[k+1] = y[k] + h*f(t[k], y[k])

14 return t, y

16def f(t, y):

17 v = np.array([-y[0] + y[1] \

18 - np.exp(-t) \

19 + np.cos(t) \

20 - np.sin(t), \

21 2*y[0] + 3*y[1]

22 - 6*np.exp(t)

23 - 2*np.cos(t)])

24 return v

27h = 1e-2

28n = round(1./h)

29t0 = 0.

30y0 = np.array([0., 3.])

31t,y = euler(f, t0, y0, h, n)

4.1.3 Equações de Ordem Superior

Seja dado o PVI de ordem $m$


	$\displaystyle\frac{d^{m}y}{dt^{m}}=f\left(t,y,\frac{dy}{dt},\dotsc,\frac{d^{m-% 1}y}{dt^{m-1}}\right),$		(4.61a)
	$\displaystyle y(t_{0})=y_{0},\left.\frac{dy}{dt}\right\|_{t=0}=y^{\prime}_{0},% \dotsc,\left.\frac{d^{(m-1)}y}{dt^{(m-1)}}\right\|_{t=0}=y^{(m-1)}_{0},$		(4.61b)

para $t_{0}\leq t\leq t_{f}$ .

Para resolvê-lo com o Método de Euler, a ideia é reescrevê-lo como um sistema de EDOs de primeira ordem com condições iniciais. Isso pode ser feito com a mudança de variáveis

	$\displaystyle u_{1}=y,$		(4.62)
	$\displaystyle u_{2}=\frac{dy}{dt},$		(4.63)
	$\displaystyle u_{3}=\frac{d^{2}y}{dt^{2}},$		(4.64)
	$\displaystyle\qquad\vdots$		(4.65)
	$\displaystyle u_{m}=\frac{d^{m-1}y}{dt^{m-1}}.$		(4.66)

Com isso e do PVI (4.61), obtemos o sistema de EDOs de primeira ordem


	$\displaystyle u^{\prime}_{1}=u_{2},$		(4.67a)
	$\displaystyle u^{\prime}_{2}=u_{3},$		(4.67b)
	$\displaystyle u^{\prime}_{3}=u_{4},$		(4.67c)
	$\displaystyle\qquad\vdots$		(4.67d)
	$\displaystyle u^{\prime}_{m}=f(t,u_{1},u_{2},\dotsc,u_{m}),$		(4.67e)

para $t_{0}<t\leq t_{f}$ e com condições inicias


	$\displaystyle u_{1}(t_{0})=y_{0},$		(4.68a)
	$\displaystyle u_{2}(t_{0})=y^{\prime}_{0},$		(4.68b)
	$\displaystyle u_{3}(t_{0})=y^{\prime\prime}_{0},$		(4.68c)
	$\displaystyle\qquad\vdots$		(4.68d)
	$\displaystyle u_{m}(t_{0})=y^{(m-1)}_{0}.$		(4.68e)

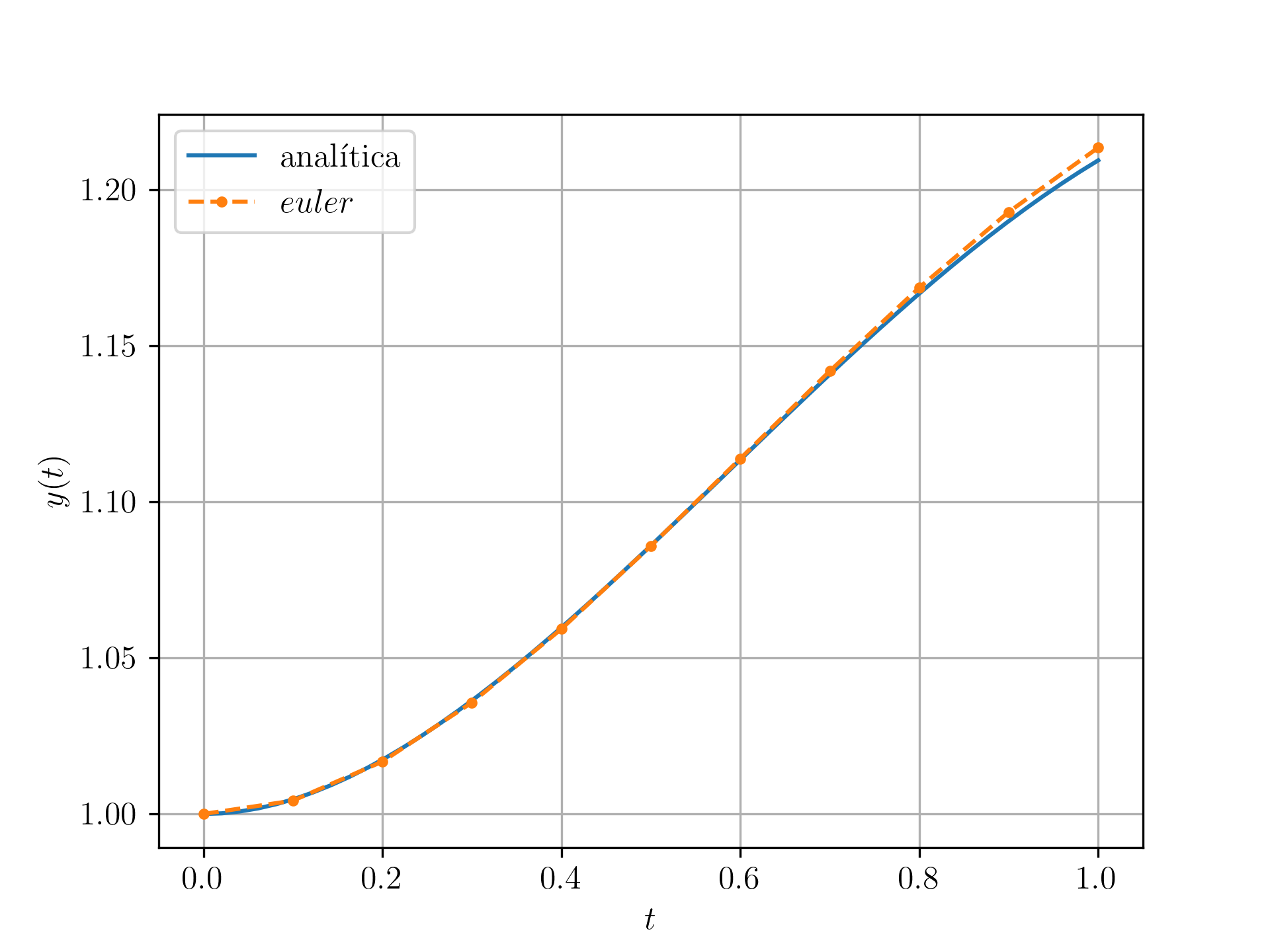
Exemplo 4.1.4.

Consideramos o seguinte PVI de ordem superior


	$\displaystyle y^{\prime\prime}-ty^{\prime}+y=(2+t)e^{-t}-t\cos(t),0<t\leq 1,$		(4.69a)
	$\displaystyle y(0)=1,y^{\prime}(0)=0.$		(4.69b)

Sua solução analítica é

y(t)=\operatorname{sen}(t)+e^{-t}.

(4.70)

Para reescrevê-lo como uma sistema de EDOs de primeira ordem, tomamos as mudanças de variáveis $u_{1}=y$ e $u_{2}=y^{\prime}$ . Com isso, obtemos


	$\displaystyle u^{\prime}_{1}=u_{2},$		(4.71a)
	$\displaystyle u_{2}^{\prime}=tu_{2}-u_{1}+(2+t)e^{-t}-t\cos(t),$		(4.71b)

para $0<t\leq t_{f}$ e com condições iniciais


	$\displaystyle u_{1}(0)=1,$		(4.72a)
	$\displaystyle u_{2}(0)=0.$		(4.72b)

Com passo $h=10^{-2}$ , o Método de Euler aplicado a este sistema fornece a solução do PVI mostrada na figura abaixo.

4.1.4 Exercícios

E. 4.1.1.

O problema de valor inicial


	$\displaystyle y^{\prime}=\pi\left[\cos^{2}(\pi t)-\operatorname{sen}^{2}(\pi t% )\right],\leavevmode\nobreak\ 0<t\leq 1.5,$		(4.73a)
	$\displaystyle y(0)=0.$		(4.73b)

tem solução analítica $y(t)=\operatorname{sen}(\pi t)\cos(\pi t)$ . Compute a aproximação $\tilde{y}(1.5;h)\approx y(1.5)$ pelo método de Euler com passo $h=10^{-1}$ e forneça o erro $e(1.5;h):=\left|\tilde{y}(1.5;h)-y(1.5)\right|$ .

$\tilde{y}(1.5)=3.14159\mathrm{e}\!-\!1$ , $e(1,h)=3.1E-01$

E. 4.1.2.

Use o Método de Euler para computar a solução de


	$\displaystyle y^{\prime}=e^{2t}-2y,\leavevmode\nobreak\ 0<t\leq 1,$		(4.74a)
	$\displaystyle y(0)=0.$		(4.74b)

Escolha um passo $h$ adequado de forma que $y(1)$ seja computado com precisão de $5$ dígitos significativos.

$h=10^{-6}$ , $\tilde{y}(1)=1.8134\mathrm{e}\!+\!0$

E. 4.1.3.

Considere o seguinte problema de valor inicial


	$\displaystyle y^{\prime}+e^{-y^{2}+1}=2,\leavevmode\nobreak\ 1<t\leq 2,$		(4.75a)
	$\displaystyle y(1)=-1.$		(4.75b)

Use o Método de Euler para computar o valor aproximado de $y(2)$ com precisão de $6$ dígitos significativos.

$-5.99605\mathrm{e}\!-\!01$

E. 4.1.4.

Use o Método de Euler para computar a solução de


	$\displaystyle y^{\prime}=-30y,\quad 0<t\leq 1,$		(4.76a)
	$\displaystyle y(0)=\frac{1}{3}$		(4.76b)

A solução analítica é $y(t)=\frac{1}{3}e^{-30t}$ . Compute a solução aproximação $\tilde{y}(1)$ e o erro $|\tilde{y}(1)-y(1)|$ usando o passo $h=10^{-1}$ . O erro obtido está de acordo com a estimativa (4.45)?

$|\tilde{y}(1)-y(1)|=3.4\mathrm{e}\!+\!2$ . Dica: verifique as hipóteses do Teorema 4.1.1.

E. 4.1.5.

Para o sistema de EDOs do Exemplo 4.1.3, verifique a ordem de convergência do Método de Euler computando o erro $\varepsilon=\|\tilde{\boldsymbol{y}}(1)-\boldsymbol{y}(1)\|$ com diferentes tamanhos de passos $h=10^{-1},10^{-2},\dotsc,10^{-6}$ .

$h$	$\tilde{\boldsymbol{y}}(1)$	$\\|\tilde{\boldsymbol{y}}(1)-\boldsymbol{y}(1)\\|$
$10^{-1}$	$(2.387,5.077)$	$7.4\mathrm{e}\!-\!1$
$10^{-2}$	$(2.500,5.693)$	$1.1\mathrm{e}\!-\!1$
$10^{-3}$	$(2.520,5.793)$	$1.2\mathrm{e}\!-\!2$
$10^{-4}$	$(2.523,5.803)$	$1.2\mathrm{e}\!-\!3$
$10^{-5}$	$(2.523,5.804)$	$1.2\mathrm{e}\!-\!4$
$10^{-6}$	$(2.523,5.804)$	$1.2\mathrm{e}\!-\!5$

E. 4.1.6.

Para o PVI de segunda ordem dado no Exemplo 4.1.4, tente computar a solução para tempos finais $t_{f}=2,3,\dotsc,5$ . Faça uma comparação gráfica entre as soluções numérica e analítica. O que ocorre ao aumentarmos o tempo final? Justifique sua resposta.

Dica: O PVI do Exemplo 4.1.4 é um problema rígido.

Análise Numérica

E. 4.1.7.

Mostre que se $\delta>-1$ , então $0<1+\delta\leq e^{\delta}$ .

Dica: use o polinômio de Taylor de grau 2 de $e^{\delta}$ .

E. 4.1.8.

Seja dado um PVI (4.3), $t_{0}\leq t\leq t_{f}$ . Sejam $\tilde{y}^{(k)}$ , $k=0,1,2,\dotsc,n$ , as aproximações computadas conforme em (4.53), com $\delta^{(k)}<\delta$ . Assumindo as mesmas hipóteses do Teorema 4.1.1, mostre a estimativa de erro global (4.54).

Dica: estude a demonstração do Teorema 4.1.1.

E. 4.1.9.

Assumindo um erro de arredondamento máximo de $\delta>0$ , use (4.54) para obter uma estimativa para a melhor escolha de $h$ .

$h=\sqrt{2\delta/M}$ . Dica: Encontre o mínimo de $E(h):=M/2+\delta/h^{2}$ .

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Política de uso de dados

Política de uso de dados

Matemática Numérica II

4.1 Método de Euler

Exemplo 4.1.1.

4.1.1 Análise Numérica

Consistência

Definição 4.1.1.

Observação 4.1.1.

Convergência

Lema 4.1.1.

Demonstração.

Teorema 4.1.1.

Demonstração.

Observação 4.1.2.

Exemplo 4.1.2.

Erros de Arredondamento

4.1.2 Sistemas de Equações

Exemplo 4.1.3.

4.1.3 Equações de Ordem Superior

Exemplo 4.1.4.

4.1.4 Exercícios

E. 4.1.1.

E. 4.1.2.

E. 4.1.3.

E. 4.1.4.

E. 4.1.5.

E. 4.1.6.

Análise Numérica

E. 4.1.7.

E. 4.1.8.

E. 4.1.9.

Envie seu comentário