Equações Diferenciais Ordinárias

2 EDO de primeira ordem 2 EDO de primeira ordem 2.2 Equação separável

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

2.1 Equação linear

A forma geral de uma EDO linear de primeira ordem é

P(t)\frac{dy}{dt}+Q(t)y=G(t),

(2.1)

onde $P(t)\neq 0$ , $Q(t)$ e $G(t)$ são funções de $t$ . Esta pode ser reescrita na forma

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}{\frac{dy}{dt% }+p(t)y=g(t)},

(2.2)

escolhendo $p(t)=Q(t)/P(t)$ e $g(t)=G(t)/P(t)$ .

2.1.1 EDO autônoma e homogênea

Primeiramente, vamos considerar o caso em que $p(t)\equiv a\neq 0$ (constante) e $g(t)\equiv 0$ , i.e.

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}{\frac{dy}{dt% }+ay=0.}

(2.3)

Observamos que $y(t)\equiv 0$ é solução trivial. Agora, para $y(t)\neq 0$ , podemos reescrever esta equação da seguinte forma

	$\displaystyle\frac{dy}{dt}$	$\displaystyle=-ay$		(2.4)
	$\displaystyle\frac{1}{y}\frac{dy}{dt}$	$\displaystyle=-a$		(2.5)

Integrando em relação a $t$ , obtemos

$\displaystyle\int\frac{1}{y}\frac{dy}{dt}\,dt$	$\displaystyle=-\int a\,dt$	(2.6)
$\displaystyle\ln\|y\|$	$\displaystyle=-at+c$	(2.7)
$\displaystyle e^{\ln\|y\|}$	$\displaystyle=e^{-at+c}$	(2.8)
$\displaystyle e^{\ln\|y\|}$	$\displaystyle=e^{-at}e^{c}$	(2.9)
$\displaystyle\|y\|$	$\displaystyle=ce^{-at},$	(2.10)

onde $c$ é uma constante indeterminada. Da definição do valor absoluto, temos esta última equação nos fornece que

	$\displaystyle y>0$		(2.11)
	$\displaystyle\Rightarrow y=\|y\|=ce^{-at}$		(2.12)

	$\displaystyle y<0$		(2.13)
	$\displaystyle\Rightarrow-y=\|y\|=ce^{-at}$		(2.14)
	$\displaystyle\Rightarrow y=-ce^{-at}.$		(2.15)

Lembrando que $c$ é uma constante indeterminada, em qualquer caso, temos

y(t)=ce^{-at}.

(2.16)

Observamos, ainda, que tomando $c=0$ esta última equação também engloba a solução trivial $y(t)\equiv 0$ .

Portanto, concluímos que a solução geral de (2.3) é

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}{y(t)=ce^{-at% }.}

(2.17)

Exemplo 2.1.1.

Vamos resolver o seguinte Problema de Valor Inicial (PVI)

	$\displaystyle y^{\prime}-y=0,\quad t>0,$		(2.18)
	$\displaystyle y(0)=1.$		(2.19)

Começamos calculando a solução geral da EDO:

$\displaystyle y^{\prime}$	$\displaystyle=y$	(2.20)
$\displaystyle\frac{1}{y}\frac{dy}{dt}$	$\displaystyle=1$	(2.21)
$\displaystyle\int\frac{1}{y}\frac{dy}{dt}\,dt$	$\displaystyle=\int 1\,dt$	(2.22)
$\displaystyle\ln\|y\|$	$\displaystyle=t+c$	(2.23)
$\displaystyle e^{\ln\|y\|}$	$\displaystyle=e^{t+c}$	(2.24)
$\displaystyle y(t)$	$\displaystyle=ce^{t}.$	(2.25)

Por fim, aplicamos a condição inicial

$\displaystyle y(0)$	$\displaystyle=1$	(2.27)
$\displaystyle ce^{0}$	$\displaystyle=1$	(2.28)
$\displaystyle c$	$\displaystyle=1$	(2.29)

Concluímos que a solução do PVI é

y(t)=e^{t}.

(2.30)

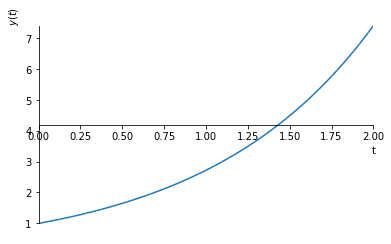
Refer to caption — Figura 2.1: Solução do problema de valor inicial tratado no Exemplo 2.1.1.

No Python, podemos computar a solução solução geral da EDO com os seguintes comandos:

⬇

1 In : from sympy import *

2 In : t = symbols('t')

3 In : y = symbols('y', cls=Function)

4 In : edo = Eq(y(t).diff(t)-y(t),0)

5 In : sol = dsolve(edo,y(t))

6 In : sol

7 Out: Eq(y(t), C1*exp(t))

Então, para aplicarmos a condição inicial e obtermos a solução do PVI, usamos:

⬇

1 In : C1 = symbols('C1')

2 In : cs = solve(Eq(sol.rhs.subs(t,0),1),dict=True)

3 In : cs

4 Out: [{C1: 1}]

6 In : sol = sol.subs(cs[0])

7 In : sol

8 Out: Eq(y(t), exp(t))

O esboço do gráfico da solução pode ser produzido com:

⬇

1 In: plot(sol.rhs, (t,0, 2), ylabel='$y(t)$')

2.1.2 Método dos fatores integrantes

Assista no YouTube

Assista no archive.org!

Escute a audioleitura!

Vejamos, agora, o caso de uma EDO da forma

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}{\frac{dy}{dt% }+ay=g(t).}

(2.31)

O método dos fatores integrantes consiste em multiplicarmos a equação por uma função $\mu=\mu(t)$ (fator integrante) de forma que

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}{\mu\frac{dy}% {dt}+\mu ay=\frac{d}{dt}\left(\mu y\right).}

(2.32)

Pela regra do produto para derivada, temos que

\mu\frac{dy}{dt}+\mu ay=\mu\frac{dy}{dt}+\mu^{\prime}y.

(2.33)

Ou seja, tal função $\mu$ deve satisfazer a seguinte EDO

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}{\mu^{\prime}% =a\mu.}

(2.34)

Usando o mesmo procedimento utilizado para (2.3), obtemos que

\mu(t)=ce^{at}.

(2.35)

Observamos que qualquer escolha de $c\neq 0$ é apropriada e, por simplicidade, escolhemos $c=1$ . Ou seja, escolhemos o fator integrante

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}{\mu(t)=e^{at% }}.

(2.36)

Agora, retornamos a equação (2.31). Multiplicando-a pelo fator integrante $\mu(t)=e^{at}$ , obtemos

	$\displaystyle\mu\frac{dy}{dt}+\mu ay=\mu g(t)$		(2.37)
	$\displaystyle\frac{d}{dt}\left(\mu y\right)=\mu g(t)$		(2.38)
	$\displaystyle\int\,d(\mu y)=\int\mu g(t)\,dt$		(2.39)
	$\displaystyle\mu y=\int\mu g(t)\,dt+c$		(2.40)
	$\displaystyle y=\frac{1}{\mu}\left[\int\mu g(t)\,dt+c\right].$		(2.41)

Portanto, concluímos que

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}{y(t)=e^{-at}% \left[\int g(t)e^{at}\,dt+c\right]}

(2.43)

é a solução geral de (2.31).

Exemplo 2.1.2.

Vamos calcular a solução geral da seguinte EDO

y^{\prime}-y=1.

(2.44)

Aplicando o método dos fatores integrantes, temos

	$\displaystyle\mu y^{\prime}-\mu y$	$\displaystyle=(\mu y)^{\prime}$		(2.45)
		$\displaystyle=\mu^{\prime}y+\mu y^{\prime}.$		(2.46)

Ou seja, devemos escolher $\mu$ tal que

	$\displaystyle\mu^{\prime}=-\mu$		(2.47)
	$\displaystyle\frac{1}{\mu}\frac{d\mu}{dt}=-1$		(2.48)
	$\displaystyle\int\frac{1}{\mu}\,d\mu=-\int 1\,dt$		(2.49)
	$\displaystyle\ln\|\mu\|=-t+c$		(2.50)
	$\displaystyle\mu=ce^{-t}$		(2.51)

Por simplicidade, escolhemos $\mu=e^{-t}$ .

Com isso, a EDO (2.44) pode ser reescrita como

	$\displaystyle\frac{d}{dt}\left(\mu y\right)=\mu\cdot 1$		(2.52)
	$\displaystyle\frac{d}{dt}\left(e^{-t}y\right)=e^{-t}.$		(2.53)

Integrando, obtemos

	$\displaystyle e^{-t}y=\int e^{-t}\,dt$		(2.54)
	$\displaystyle e^{-t}y(t)=-e^{-t}+c$		(2.55)
	$\displaystyle y(t)=-e^{t}e^{-t}+ce^{t}$		(2.56)
	$\displaystyle y(t)=-1+ce^{t},$		(2.57)

a qual é a solução geral. A figura abaixo contém esboços dos gráficos da solução geral para diferentes valores de $c$ .

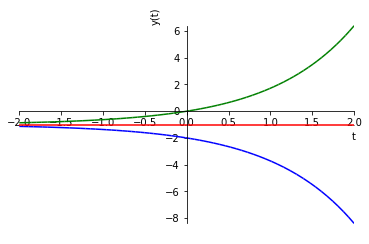
No Python, podemos computar a solução solução geral da EDO e fazer o gráfico acima com os seguintes comandos:

⬇

1 In : from sympy import *

2 In : y = symbols('y', cls=Function)

3 In : t,C1 = symbols('t,C1')

4 In : edo = Eq(diff(y(t),t)-y(t),1)

5 In : sg = dsolve(edo)

6 In : sg

7 Out: Eq(y(t), C1*exp(t) - 1)

9 In : p = plot(sg.rhs.subs(C1,-1), (t,-2,2), \

10 ...: ylabel='y(t)', line_color='blue', show=False)

11 ...:

12 In : q = plot(sg.rhs.subs(C1,0), (t,-2,2), \

13 ...: ylabel='y(t)', line_color='red', show=False)

14 ...:

15 In : p.extend(q)

16 In : q = plot(sg.rhs.subs(C1,1), (t,-2,2), \

17 ...: ylabel='y(t)', line_color='green', show=False)

18 ...:

19 In : p.extend(q)

20 In : p.show()

2.1.3 Caso geral

Assista no YouTube

Assista no archive.org!

Escute a audioleitura!

O caso geral de uma EDO linear de primeira ordem

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}{y^{\prime}+p% (t)y=g(t)}

(2.58)

também pode ser resolvido pelo método dos fatores integrantes. Neste caso, o fator integrante $\mu=\mu(t)$ deve ser escolhido de forma que

	$\displaystyle\mu y^{\prime}+\mu p(t)y=(\mu y)^{\prime}$		(2.59)
	$\displaystyle{\color[rgb]{1,0,0}\definecolor[named]{pgfstrokecolor}{rgb}{1,0,0% }\mu y^{\prime}}+{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{% 0,0,1}\mu p(t)}y={\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{% 0,0,1}\mu^{\prime}}y+{\color[rgb]{1,0,0}\definecolor[named]{pgfstrokecolor}{% rgb}{1,0,0}\mu y^{\prime}},$		(2.60)

ou seja

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\mu^{\prime}% =p(t)\mu}.

(2.61)

Integrando, obtemos o fator integrante

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}{\mu(t)=e^{% \int p(t)\,dt}.}

(2.62)

Usando este fator integrante, a equação (2.58) pode ser reescrita da seguinte maneira

\frac{d}{dt}\left(\mu y\right)=\mu g(t).

(2.63)

Integrando, obtemos a solução geral

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}{y(t)=\frac{1% }{\mu(t)}\left[\int\mu(t)g(t)\,dt+c\right].}

(2.64)

Exemplo 2.1.3.

Vamos calcular a solução geral da seguinte EDO

y^{\prime}+\frac{1}{t}y=t.

(2.65)

Primeiramente, calculamos o fator integrante $\mu=\mu(t)$ tal que

\mu y^{\prime}+{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{% 0,0,1}\mu\frac{1}{t}}y=(\mu y)^{\prime}={\color[rgb]{0,0,1}\definecolor[named]% {pgfstrokecolor}{rgb}{0,0,1}\mu^{\prime}}y+\mu y^{\prime}.

(2.66)

Ou seja, precisamos que

\mu^{\prime}=\frac{1}{t}\mu.

(2.67)

Integrando, obtemos

$\displaystyle\mu(t)$	$\displaystyle=e^{\int\frac{1}{t}\,dt}$	(2.68)
	$\displaystyle=e^{\ln\|t\|}$	(2.69)
	$\displaystyle=t$	(2.70)

Aplicando o fator integrante a EDO (2.65), obtemos

	$\displaystyle\frac{d}{dt}\left(ty\right)=t^{2}$		(2.71)
	$\displaystyle ty=\int t^{2}\,dt$		(2.72)
	$\displaystyle y=\frac{1}{t}\left[\frac{t^{3}}{3}+c\right]$		(2.73)
	$\displaystyle y=\frac{t^{2}}{3}+\frac{c}{t}$		(2.74)

2.1.4 Aplicação em modelagem

Exemplo 2.1.4.

(Mistura em tanque) No instante inicial $t=0$ s (segundo), um tanque contem $q_{0}$ kg (quilograma) de sal dissolvido em $l$ L (litro) de água. Uma solução de $s$ kg/L de sal e água entra no tanque a uma taxa de $r$ L/s. Esta solução mistura-se com o líquido presente no tanque e a mistura final sai do tanque a mesma taxa de $r$ L/s.

Vamos modelar a quantidade de sal $q$ kg presente no tanque a cada instante $t$ s. Temos que $q$ é função do tempo $t$ s, i.e. $q=q(t)$ . A condição inicial é

q(0)=q_{0}.

(2.75)

A taxa de variação de $q$ no tempo é $dq/dt$ e é modelada por

\frac{dq}{dt}=\underbrace{sr}_{\text{taxa de entrada}}-\underbrace{\frac{q}{l}% r}_{\text{taxa de saída}}.

(2.76)

Ou seja, o problema é modelado como o seguinte PVI

	$\displaystyle\frac{dq}{dt}=sr-\frac{q}{l}r,\quad t>0,$		(2.77)
	$\displaystyle q(0)=q_{0},$		(2.78)

onde $s$ , $r$ , $l$ e $q_{0}$ são parâmetros do problema. A EDO relacionada é linear de primeira ordem e, portanto, pode ser resolvida pelo método dos fatores integrantes. Veja o ER.2.1.3.

Exemplo 2.1.5.

(Objeto em queda livre) Seja $m$ kg a massa de um objeto em queda livre em um meio com resistência de $\gamma$ kg/s e aceleração da gravidade de $g$ m/s². A segunda lei de Newton é a lei física que estabelece que a força total atuando sobre o objeto é igual a sua massa multiplicada por sua aceleração. Desta forma, obtemos

\underbrace{m\frac{dv}{dt}}_{\text{massa}\times\text{aceleração}}=\underbrace{% mg}_{\text{força da gravidade}}-\underbrace{\gamma v}_{\text{força da resistê% ncia}]},

(2.79)

onde $v=v(t)$ m/s é a velocidade do objeto (sentido positivo igual ao da força da gravidade). Assumindo que o objeto tem velocidade $v_{0}$ m/s no instante inicial $t=0$ , o modelo resume-se ao seguinte PVI:

	$\displaystyle m\frac{dv}{dt}=mg-\gamma v,\quad t>0,$		(2.80)
	$\displaystyle v(0)=v_{0},$		(2.81)

onde $m$ , $g$ , $\gamma$ e $v_{0}$ são parâmetros.

Exercícios resolvidos

ER 2.1.1.

Resolva o seguinte PVI

	$\displaystyle y^{\prime}+y=1,\quad t>0,$		(2.82)
	$\displaystyle y(0)=2.$		(2.83)

Resolução.

Primeiramente, obtemos a solução geral da EDO pelo método dos fatores integrante. Para tanto, buscamos pelo fator integrante $\mu$ tal que

\mu y^{\prime}+\mu y=(\mu y)^{\prime},

(2.84)

ou seja,

	$\displaystyle\mu^{\prime}=\mu$		(2.85)
	$\displaystyle\mu(t)=e^{t}.$		(2.86)

Obtido o fator integrante, reescrevemos a EDO como segue

	$\displaystyle\frac{d}{dt}\left(\mu y\right)=\mu\cdot 1$		(2.87)
	$\displaystyle\frac{d}{dt}\left(e^{t}y\right)=e^{t}.$		(2.88)

Integrando, obtemos a solução geral

y=1+ce^{-t}.

(2.89)

Aplicando a condição inicial, obtemos

	$\displaystyle y(0)=2$		(2.90)
	$\displaystyle 1+ce^{-0}=2$		(2.91)
	$\displaystyle c=1.$		(2.92)

Concluímos que a solução do PVI é $y(t)=1+e^{-t}$ .

ER 2.1.2.

Calcule a solução geral da EDO

\displaystyle y^{\prime}+\frac{1}{t}y=\operatorname{sen}(t),\quad t>0.

(2.93)

Resolução.

Buscamos pelo fator integrante $\mu$ tal que

\mu y^{\prime}+\mu\frac{1}{t}y=(\mu y)^{\prime},

(2.94)

ou seja,

	$\displaystyle\mu^{\prime}=\frac{\mu}{t}$		(2.95)
	$\displaystyle\mu(t)=e^{\int\frac{1}{t}\,dt}=e^{\ln\|t\|}=t.$		(2.96)

Obtido o fator integrante, reescrevemos a EDO como segue

	$\displaystyle\frac{d}{dt}\left(\mu y\right)=\mu\cdot\operatorname{sen}(t)$		(2.97)
	$\displaystyle\frac{d}{dt}\left(ty\right)=t\operatorname{sen}(t).$		(2.98)

Integrando, obtemos a solução geral

y(t)=\frac{c}{t}+\frac{\operatorname{sen}(t)}{t}-\cos(t).

(2.99)

ER 2.1.3.

(Mistura em tanque) No instante inicial $t=0$ s (segundo), um tanque contem $100$ kg de sal dissolvidos em $1000$ L d’água. Uma solução de $0,2$ kg/L de sal e água entra no tanque a uma taxa de $10$ L/s. Esta solução mistura-se com o líquido presente no tanque e a mistura final sai do tanque a mesma taxa de $10$ L/s. Calcule a quantidade de sal misturado no tanque após $1$ hora de operação, i.e. quando $t=3600$ s.

Resolução.

Denotando por $q=q(t)$ kg a quantidade de sal misturado no tanque no instante $t$ , temos que a taxa de variação de $q$ no tempo é dada por

	$\displaystyle\frac{dq}{dt}$	$\displaystyle=0,2\cdot 10-\frac{q}{1000}\cdot 10$		(2.100)
		$\displaystyle=2-\frac{q}{100}.$		(2.101)

Ou seja, o modelo constitui-se no seguinte PVI

	$\displaystyle\frac{dq}{dt}=2-\frac{q}{100},\quad t>0,$		(2.102)
	$\displaystyle q(0)=100.$		(2.103)

Para resolver o problema, vamos usar o método dos fatores integrantes. O fator integrante é escolhido como sendo

	$\displaystyle\mu(t)$	$\displaystyle=e^{\int\frac{1}{100}\,dt}$		(2.104)
		$\displaystyle=e^{t/100}.$		(2.105)

Segue que a EDO (2.102) pode ser reescrita como

\frac{d}{dt}\left(qe^{t/100}\right)=2e^{t/100}.

(2.106)

Integrando, obtemos

$\displaystyle q(t)$	$\displaystyle=e^{-t/100}\int 2e^{t/100}\,dt$	(2.107)
	$\displaystyle=e^{-t/100}\left(200e^{t/100}+c\right)$	(2.108)
	$\displaystyle=200+ce^{-t/100}.$	(2.109)

Da condição inicial, obtemos

	$\displaystyle q(0)=100$		(2.110)
	$\displaystyle 200+c=100$		(2.111)
	$\displaystyle c=-100.$		(2.112)

Logo, a solução do PVI é

q(t)=200-100e^{-t/100}.

(2.113)

No tempo $t=3600$ s, temos

q(3600)=200-100e^{-3600/100}\approx 200\leavevmode\nobreak\ \text{kg}.

(2.114)

Exercícios

E. 2.1.1.

Calcule a solução do seguinte PVI

	$\displaystyle y^{\prime}+y=0,\quad t>0,$		(2.115)
	$\displaystyle y(0)=1.$		(2.116)

$y(t)=e^{-t}$

E. 2.1.2.

Calcule a solução do seguinte PVI

	$\displaystyle y^{\prime}-y=2,\quad t>0,$		(2.117)
	$\displaystyle y(0)=1.$		(2.118)

$y(t)=3e^{t}-2$

E. 2.1.3.

Calcule a solução geral da seguinte EDO

y^{\prime}+y=\operatorname{sen}(t).

(2.119)

$y(t)=ce^{-t}+\frac{\operatorname{sen}(x)}{2}-\frac{\cos(x)}{2}$

E. 2.1.4.

Calcule a solução geral do seguinte PVI

	$\displaystyle y^{\prime}+\frac{1}{t}y=2t,\quad t>1,$		(2.120)
	$\displaystyle y(1)=0.$		(2.121)

$y(t)=\frac{2}{3}\left(t^{2}-\frac{1}{t}\right)$

E. 2.1.5.

Calcule a solução geral do seguinte PVI

	$\displaystyle ty^{\prime}+2y=1,\quad t>1,$		(2.122)
	$\displaystyle y(1)=1.$		(2.123)

$y(t)=\frac{1}{2}\left(\frac{1}{t^{2}}+1\right)$

E. 2.1.6.

Seja um objeto de massa $m=1$ kg em queda livre sujeito a aceleração da gravidade de $9,8$ m/s² e resistência do meio de $\gamma=0,2$ kg/s. Assuma, ainda, que o objeto está em repouso no tempo inicial e a uma altura de $10$ m (metros) do solo. Quanto tempo leva para o objeto atingir o solo.

$1.5$ s

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Política de uso de dados

Política de uso de dados

Equações Diferenciais Ordinárias

2.1 Equação linear

2.1.1 EDO autônoma e homogênea

Exemplo 2.1.1.

2.1.2 Método dos fatores integrantes

Exemplo 2.1.2.

2.1.3 Caso geral

Exemplo 2.1.3.

2.1.4 Aplicação em modelagem

Exemplo 2.1.4.

Exemplo 2.1.5.

Exercícios resolvidos

ER 2.1.1.

Resolução.

ER 2.1.2.

Resolução.

ER 2.1.3.

Resolução.

Exercícios

E. 2.1.1.

E. 2.1.2.

E. 2.1.3.

E. 2.1.4.

E. 2.1.5.

E. 2.1.6.

Envie seu comentário