Cálculo I

3 Derivadas 3 Derivadas 3.2 Função derivada

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

3.1 Derivada no ponto

Vamos estudar a definição de derivada de uma função em um ponto. Começaremos pelas noções de reta secante e de reta tangente ao gráfico de uma função. Em seguida, estudaremos as noções de taxa de variação média e taxa de variação instantânea. Por fim, definiremos a derivada de uma função em um ponto.

3.1.1 Retas secante e tangente

Definimos a reta secante ao gráfico de uma dada função $f$ pelos pontos ${\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}x_{0}}$ e ${\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}x_{1}}$ , $x_{0}\neq x_{1}$ , como sendo a reta determinada pela equação

y=\underbrace{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1% }\frac{f(x_{1})-f(x_{0})}{x_{1}-x_{0}}}_{m_{\text{sec}}}(x-{\color[rgb]{0,0,1}% \definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}x_{0}})+f({\color[rgb]{0,0,1}% \definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}x_{0}}).

(3.1)

I.e., é a reta que passa pelos pontos $(x_{0},f(x_{0}))$ e $(x_{1},f(x_{1}))$ . Consultemos a Figura 3.1. O coeficiente angular da reta secante é

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\color[rgb]{% 0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}m_{\text{sec}}=\frac{f(x_% {1})-f(x_{0})}{x_{1}-x_{0}}.

(3.2)

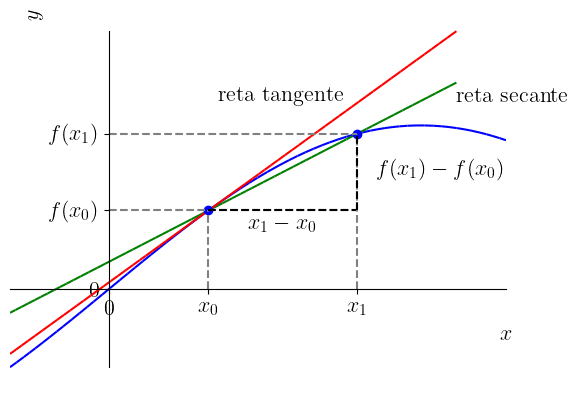
Refer to caption — Figura 3.1: Reta secante (linha traço-ponto) e da reta tangente (linha tracejada) ao gráfico de uma função (linha contínua).

A reta tangente ao gráfico de uma função $f$ em $x={\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}x_{0}}$ é a reta que passa pelo ponto $\left({\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}x_{0}}% ,{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}f(x_{0})}\right)$ e tem coeficiente angular

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}m_{\text{tg}}% =\lim_{x_{1}\to x_{0}}\frac{f(x_{1})-f(x_{0})}{x_{1}-x_{0}}.

(3.3)

I.e., a reta de equação

y={\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}m_{\text{% tg}}}(x-{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}x_{0% }})+{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}f(x_{0})}.

(3.4)

Menos formal, é a reta limite das retas secantes ao gráfico da função pelos pontos $x_{0}$ e $x_{1}$ , quando $x_{1}\to x_{0}$ . Consultemos a Figura 3.1.

Fazendo a mudança de variável $h=x_{1}-x_{0}$ , temos que (3.3) é equivalente a

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}m_{\text{tg}}% =\lim_{h\to 0}\frac{f(x_{0}+h)-f(x_{0})}{h}.

(3.5)

De fato, da mudança de variável, temos que $x_{1}=x_{0}+h$ e quando $x_{1}\to x_{0}$ , temos que $h=x_{1}-x_{0}\to 0$ . Ou seja,

	$\displaystyle m_{\text{tg}}=\lim_{x_{1}\to x_{0}}\frac{f(x_{1})-f(x_{0})}{x_{1% }-x_{0}}$		(3.6)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{f(x_{0}+h)-f(x_{0})}{h}.$		(3.7)

Exemplo 3.1.1.

Sejam $f(x)=x^{2}$ e $x_{0}=1$ . O coeficiente angular da reta secante ao gráfico de $f$ pelos pontos $x_{0}=1$ e $x_{1}=2$ é

	$\displaystyle m_{\text{sec}}=\frac{f(x_{1})-f(x_{0})}{x_{1}-x_{0}}$		(3.8)
	$\displaystyle\text{}\quad=\frac{f(2)-f(1)}{2-1}$		(3.9)
	$\displaystyle\text{}\quad=\frac{4-1}{1}=3.$		(3.10)

Logo, a reta secante ao gráfico de $f$ pelos pontos $x_{0}=1$ e $x_{1}=2$ tem equação

	$\displaystyle y=m_{\text{sec}}(x-x_{0})+f(x_{0})$		(3.11)
	$\displaystyle y=3(x-1)+f(1)$		(3.12)
	$\displaystyle y=3x-2.$		(3.13)

Na Figura 3.2, temos os gráficos da função e da reta secante.

Código 29: Python

⬇

1from sympy import Symbol, Lambda

2x = Symbol('x')

3x0 = 1

4x1 = 2

5f = Lambda(x, x**2)

6m_sec = (f(x1)-f(x0))/(x1-x0)

7r_sec = Lambda(x, m_sec*(x - x0) + f(x0))

8print(f"Reta secante: y = {r_sec(x)}")

Reta secante: y = 3*x - 2

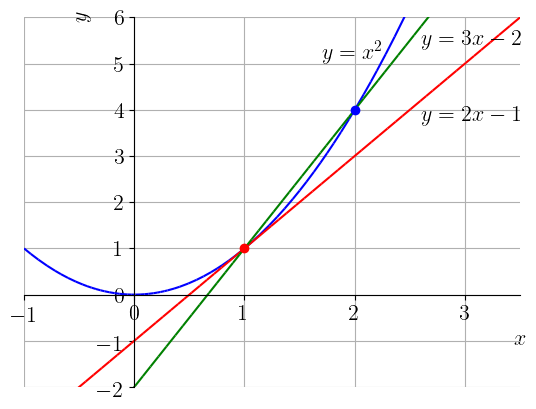
Agora, o coeficiente angular da reta tangente ao gráfico de $f$ no ponto $x_{0}$ é

	$\displaystyle m_{\text{tg}}=\lim_{h\to 0}\frac{f(x_{0}+h)-f(x_{0})}{h}$		(3.14)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{(1+h)^{2}-1}{h}$		(3.15)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{1+2h+h^{2}-1}{h}$		(3.16)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{2+h}{1}=2.$		(3.17)

Assim sendo, a reta tangente ao gráfico de $f(x)=x^{2}$ no ponto $x_{0}=1$ tem coeficiente angular $m_{\text{tg}}=2$ e equação

y=2(x-1)+1=2x-1.

(3.18)

Na Figura 3.2, temos os gráficos da função e da reta tangente.

Código 30: Python

⬇

1from sympy import symbols, Lambda, limit

2x, h = symbols('x,h')

3x0 = 1

4x1 = 2

5f = Lambda(x, x**2)

6m_tg = limit((f(x0+h)-f(x0))/h, h, 0)

7r_tg = Lambda(x, m_tg*(x - x0) + f(x0))

8print(f"Reta tangente: y = {r_tg(x)}")

Reta tangente: y = 2*x - 1

3.1.2 Taxa de variação

hlA taxa de variação média de uma função $f$ quando $x$ varia de $x_{0}$ a $x_{1}$ é definida como

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\frac{\Delta y% }{\Delta x}:=\frac{f(x_{1})-f(x_{0})}{x_{1}-x_{0}}.

(3.19)

Desta deriva-se a taxa de variação instantânea de $f$ no ponto $x_{0}$ , a qual é definida como

	$\displaystyle\left.\frac{\mathrm{d}f}{\mathrm{d}x}\right\|_{x=x_{0}}:=\lim_{x% \to x_{0}}\frac{f(x)-f(x_{0})}{x-x_{0}}$		(3.20)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{f(x_{0}+h)-f(x_{0})}{h}.$		(3.21)

Em muitas áreas do conhecimento, estas taxas recebem nomes específicos.

Exemplo 3.1.2.(Velocidade)

Seja $s=s(t)$ a função distância percorrida por um objeto no tempo. A velocidade média (taxa de variação média da distância) do tempo $t_{0}$ ao tempo $t_{1}$ é

\frac{\Delta s}{\Delta t}=\frac{s(t_{1})-s(t_{0})}{t_{1}-t_{0}}.

(3.22)

Por exemplo, se $s(t)=15t^{2}+t$ (km), então a velocidade média do objeto entre $t_{0}=1$ h e $t_{1}=3$ h é

	$\displaystyle\frac{\Delta s}{\Delta t}=\frac{(15t_{1}^{2}+t_{1})-(15t_{0}^{2}+% t_{0})}{t_{1}-t_{0}}$		(3.23)
	$\displaystyle\text{}\quad=\frac{15\cdot 3^{2}+3-(15\cdot 1^{2}+1)}{3-1}$		(3.24)
	$\displaystyle\text{}\quad=\frac{135+3-15-1}{2}$		(3.25)
	$\displaystyle\text{}\quad=61\leavevmode\nobreak\ \frac{\text{km}}{\text{h}}.$		(3.26)

A velocidade (taxa de variação instantânea da distância) no tempo $t_{0}=1$ é

	$\displaystyle\left.\frac{\mathrm{d}s}{\mathrm{d}t}\right\|_{t=t_{0}}=\lim_{h\to 0% }\frac{s(t_{0}+h)-s(t_{0})}{h}$		(3.27)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{15(t_{0}+h)^{2}+(t_{0}+h)-\left(1% 5t_{0}^{2}+t_{0}\right)}{h}$		(3.28)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{15t_{0}^{2}+30t_{0}h+15h^{2}+t_{0% }+h-15t_{0}^{2}-t_{0}}{h}$		(3.29)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{30t_{0}h+15h^{2}+h}{h}$		(3.30)
	$\displaystyle\text{}\quad=\lim_{h\to 0}30t_{0}+15h+1$		(3.31)
	$\displaystyle\text{}\quad=30t_{0}+1=31\leavevmode\nobreak\ \frac{\text{km}}{% \text{h}}.$		(3.32)

Exemplo 3.1.3.(Custo marginal)

Seja $c(x)=\sqrt{x}$ (milhões de reais) o custo da produção em uma empresa em função do número de unidades produzidas (milhares). O custo médio da produção de $x_{0}=4$ a $x_{1}=9$ é

	$\displaystyle\frac{\Delta c}{\Delta x}=\frac{c(x_{1})-c(x_{0})}{x_{1}-x_{0}}$		(3.33)
	$\displaystyle\text{}\quad=\frac{\sqrt{x_{1}}-\sqrt{x_{0}}}{x_{1}-x_{0}}$		(3.34)
	$\displaystyle\text{}\quad=\frac{\sqrt{9}-\sqrt{4}}{9-4}$		(3.35)
	$\displaystyle\text{}\quad=\frac{3-2}{5}$		(3.36)
	$\displaystyle\text{}\quad=0,2\leavevmode\nobreak\ \frac{\text{R\$}}{\text{un}}.$		(3.37)

O custo marginal (taxa de variação instantânea do custo) quando a empresa está produzindo $x_{0}=4$ milhões de unidades é

	$\displaystyle\left.\frac{\mathrm{d}c}{\mathrm{d}x}\right\|_{x=x_{0}=4}=\lim_{h% \to 0}\frac{\sqrt{x_{0}+h}-\sqrt{x_{0}}}{h}$		(3.38)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{\sqrt{x_{0}+h}-\sqrt{x_{0}}}{h}% \cdot\frac{\sqrt{x_{0}+h}+\sqrt{x_{0}}}{\sqrt{x_{0}+h}+\sqrt{x_{0}}}$		(3.39)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{x_{0}+h-x_{0}}{h(\sqrt{x_{0}+h}+% \sqrt{x_{0}})}$		(3.40)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{1}{\sqrt{x_{0}+\cancelto{0}{h}}+% \sqrt{x_{0}}}$		(3.41)
	$\displaystyle\text{}\quad=\frac{1}{2\sqrt{x_{0}}}=\frac{\sqrt{x_{0}}}{2x_{0}}$		(3.42)
	$\displaystyle\text{}\quad=\frac{\sqrt{4}}{2\cdot 4}=0,25\leavevmode\nobreak\ % \frac{\text{R\$}}{\text{un}}.$		(3.43)

Observação 3.1.1.(Rendimento e lucro marginais)

Analogamente a custo marginal, temos as noções de rendimento marginal e lucro marginal.

3.1.3 Derivada no ponto

A derivada de uma função $f$ no ponto $x=x_{0}$ é definida por

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}f^{\prime}(x_% {0})=\left.\frac{\mathrm{d}f}{\mathrm{d}x}\right|_{x=x_{0}}:=\lim_{h\to 0}% \frac{f(x_{0}+h)-f(x_{0})}{h}.

(3.44)

Exemplo 3.1.4.

Estudemos os seguintes casos:

a)

$f(x)=k$ , $k$ constante.

$\displaystyle f^{\prime}(x_{0})=\lim_{h\to 0}\frac{f(x_{0}+h)-f(x_{0})}{h}$ (3.45)

$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{k-k}{h}=0.$ (3.46)
b)

$f(x)=x$ .

$\displaystyle f^{\prime}(x_{0})=\lim_{h\to 0}\frac{f(x_{0}+h)-f(x_{0})}{h}$ (3.47)

$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{x_{0}+h-x_{0}}{h}=1.$ (3.48)
c)

$f(x)=\sqrt{x}$ , $x_{0}=1$ .

$\displaystyle f^{\prime}(1)=\lim_{h\to 0}\frac{\sqrt{1+h}-\sqrt{1}}{h}$ (3.49)

$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{\sqrt{1+h}-\sqrt{1}}{h}\cdot\frac% {\sqrt{1+h}+\sqrt{1}}{\sqrt{1+h}+\sqrt{1}}$ (3.50)

$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{1+h-1}{h(\sqrt{1+h}+1)}=\frac{1}{% 2}.$ (3.51)

Exemplo 3.1.5.(Rendimento marginal)

Assuma que o rendimento de uma empresa é modelado por $r(x)=x^{2}$ (milhões de reais), onde $x$ é o número em milhões de unidades vendidas. O rendimento marginal quando $x=x_{0}=1$ é

	$\displaystyle r^{\prime}(x_{0})=\lim_{x\to x_{0}}\frac{(x_{0}+h)^{2}-x_{0}^{2}% }{h}$		(3.52)
	$\displaystyle\text{}\quad=\lim_{x\to x_{0}}\frac{x_{0}^{2}+2x_{0}h+h^{2}-x_{0}% ^{2}}{h}$		(3.53)
	$\displaystyle\text{}\quad=\lim_{x\to x_{0}}2x_{0}h+h=2x_{0}=2\leavevmode% \nobreak\ \frac{\text{R\$}}{\text{un}}$		(3.54)

3.1.4 Exercícios resolvidos

ER 3.1.1.

Determine a equação da reta tangente ao gráfico de $f(x)=\sqrt{x}$ no ponto $x_{0}=4$ . Faça, então, os esboços dos gráficos de $f$ e da reta tangente em um mesmo plano cartesiano.

Resolução.

A equação da reta tangente ao gráfico da função $f$ no ponto $x_{0}=4$ é

y=f^{\prime}(x_{0})(x-x_{0})+f(x_{0}).

(3.55)

A derivada de $f$ no ponto $x_{0}$ é

	$\displaystyle f^{\prime}(x_{0})=\lim_{x\to x_{0}}\frac{f(x_{0}+h)-f(x_{0})}{h}$		(3.56)
	$\displaystyle\text{}\quad=\lim_{x\to 4}\frac{\sqrt{4+h}-\sqrt{4}}{h}$		(3.57)
	$\displaystyle\text{}\quad=\lim_{x\to 4}\frac{\sqrt{4+h}-2}{h}\cdot\frac{\sqrt{% 4+h}+2}{\sqrt{4+h}+2}$		(3.58)
	$\displaystyle\text{}\quad=\lim_{x\to 4}\frac{4+h-4}{h(\sqrt{4+h}+2)}$		(3.59)
	$\displaystyle\text{}\quad=\frac{1}{\sqrt{4}+2}=\frac{1}{4}.$		(3.60)

Portanto, a equação da reta tangente é

	$\displaystyle y=\frac{1}{4}(x-4)+\sqrt{4}$		(3.61)
	$\displaystyle y=\frac{1}{4}x+1.$		(3.62)

Consultemos a Figura 3.3 para os esboços dos gráfico de $f$ e da reta tangente.

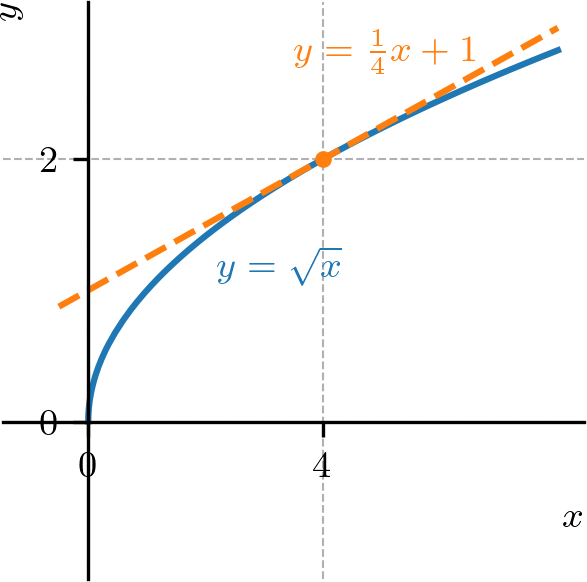
ER 3.1.2.

Considere que a produção em uma empresa tem custo

c(x)=\sqrt{x}

(3.63)

e rendimento

r(x)=x^{2},

(3.64)

onde $x$ é o número de unidades (em milhões) produzidas. Calcule o lucro marginal da empresa quando $x=1$ mi.

Resolução.

O lucro é

l(x)=r(x)-c(x).

(3.65)

Desta forma, o lucro marginal no ponto $x_{0}=1$ é

	$\displaystyle l^{\prime}(x_{0})=\lim_{h\to 0}\frac{l(x_{0}+h)-l(x_{0})}{h}$		(3.66)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{r(x_{0}+h)-c(x_{0}+h)-(r(x_{0})-c% (x_{0}))}{h}$		(3.67)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{r(x_{0}+h)-r(x_{0})-(c(x_{0}+h)-c% (x_{0}))}{h}$		(3.68)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{r(x_{0}+h)-r(x_{0})}{h}-\lim_{h% \to 0}\frac{c(x_{0}+h)-c(x_{0})}{h}$		(3.69)
	$\displaystyle\text{}\quad=r^{\prime}(x_{0})-c^{\prime}(x_{0})$		(3.70)
	$\displaystyle\text{}\quad=2x_{0}-\frac{1}{2\sqrt{x_{0}}}$		(3.71)
	$\displaystyle\text{}\quad=2-\frac{1}{2}=1,5\leavevmode\nobreak\ \frac{\text{R% \$}}{\text{un}}.$		(3.72)

3.1.5 Exercícios

E. 3.1.1.

Calcule as derivadas conforme indicado:

a)

$f(x)=2$ , $f^{\prime}(-1)$ ;
b)

$g(x)=10^{6}$ , $g^{\prime}(10^{8})$ ;
c)

$h(x)=\ln 2e$ , $h^{\prime}(-\pi)$ ;

a) $0$ ; b) $0$ ; c) $0$

E. 3.1.2.

Calcule as derivadas conforme indicado:

a)

$f(x)=2+x$ , $f^{\prime}(-1)$ ;
b)

$g(x)=10^{6}-2x$ , $g^{\prime}(-3)$ ;
c)

$h(x)=\ln(2e)+ex$ , $h^{\prime}(10^{6})$ ;

a) $1$ ; b) $-2$ ; c) $e$

E. 3.1.3.

Calcule as derivadas conforme indicado:

a)

$f(x)=x$ , $f^{\prime}(-1)$ ;
b)

$g(x)=-2x$ , $g^{\prime}(-3)$ ;
c)

$h(x)=ex$ , $h^{\prime}(10^{6})$ ;

a) $-1$ ; b) $-2$ ; c) $e$

E. 3.1.4.

Determine a reta secante ao gráfico de $f(x)=5-x^{2}$ pelos pontos $x_{0}=1$ e $x_{1}=2$ . Então, determine a reta tangente ao gráfico de $f$ no ponto $x_{0}=1$ . Por fim, faça os esboços dos gráficos de $f$ , da reta secante e da reta tangente em um mesmo plano cartesiano.

reta secante: $y=-3x+7$ ; reta tangente: $y=-2x+6$ ; dica: verifique seus esboços plotando os gráficos no computador

E. 3.1.5.

Assumindo que, em uma empresa, a produção tenha o custo $c(x)=2\sqrt{x}$ e rendimento $r(x)=\frac{1}{100}x^{3}$ , dados em milhões de reais com $x$ em milhares de unidades. Calcule:

a)

o custo marginal quando $x=1$ ;
b)

o rendimento marginal quando $x=1$ ;
c)

o lucro marginal quando $x=1$ .

a) $1000\leavevmode\nobreak\ \frac{\text{R}\$}{\text{un}}$ ; b) $30\leavevmode\nobreak\ \frac{\text{R\$}}{\text{un}}$ ; c) $-970\leavevmode\nobreak\ \frac{\text{R\$}}{\text{un}}$ .

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Política de uso de dados

Política de uso de dados

Cálculo I

3.1 Derivada no ponto

3.1.1 Retas secante e tangente

Exemplo 3.1.1.

3.1.2 Taxa de variação

Exemplo 3.1.2.(Velocidade)

Exemplo 3.1.3.(Custo marginal)

Observação 3.1.1.(Rendimento e lucro marginais)

3.1.3 Derivada no ponto

Exemplo 3.1.4.

Exemplo 3.1.5.(Rendimento marginal)

3.1.4 Exercícios resolvidos

ER 3.1.1.

Resolução.

ER 3.1.2.

Resolução.

3.1.5 Exercícios

E. 3.1.1.

E. 3.1.2.

E. 3.1.3.

E. 3.1.4.

E. 3.1.5.

Envie seu comentário

	$\displaystyle f^{\prime}(x_{0})=\lim_{h\to 0}\frac{f(x_{0}+h)-f(x_{0})}{h}$		(3.45)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{k-k}{h}=0.$		(3.46)

	$\displaystyle f^{\prime}(x_{0})=\lim_{h\to 0}\frac{f(x_{0}+h)-f(x_{0})}{h}$		(3.47)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{x_{0}+h-x_{0}}{h}=1.$		(3.48)

	$\displaystyle f^{\prime}(1)=\lim_{h\to 0}\frac{\sqrt{1+h}-\sqrt{1}}{h}$		(3.49)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{\sqrt{1+h}-\sqrt{1}}{h}\cdot\frac% {\sqrt{1+h}+\sqrt{1}}{\sqrt{1+h}+\sqrt{1}}$		(3.50)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{1+h-1}{h(\sqrt{1+h}+1)}=\frac{1}{% 2}.$		(3.51)