Política de uso de dados

Ao navegar por este site, você concorda com a política de uso de dados.

Política de uso de dados

Ao navegar por este site, você concorda com a política de uso de dados.

| | | |

Vetores

1 Fundamentos 1 Fundamentos 1.2 Definição de Vetor

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

1.1 Segmentos Orientados

O conceito de segmento orientado é fundamental na definição de vetores. Como o próprio nome indica, trata-se de definir uma orientação a um dado segmento de reta. Antes, portanto, vamos definir o que entendemos por um segmento.

1.1.1 Segmento

[[youtube:¡J-GN-uulfRs¿]]

Sejam dados dois pontos $A$ e $B$ sobre uma reta $r$ . O conjunto de todos os pontos de $r$ entre $A$ e $B$ é chamado de segmento e denotado por $A B$ . A reta $r$ é chamada de reta suporte e os pontos $A$ e $B$ de pontos extremos. Consulte a Figura 1.1.

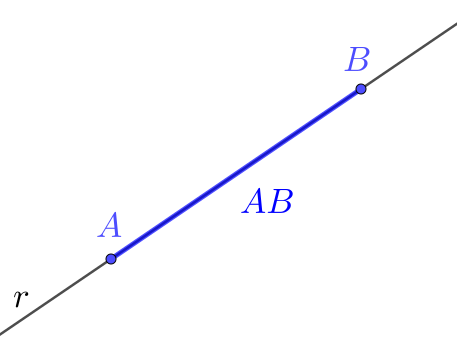
Refer to caption — Figura 1.1: Um segmento $A B$ de uma reta (direção) $r$ .

Comprimento e Direção

O comprimento de um segmento $A B$ é denotado por $|AB|$ e definido como a distância entre seus pontos extremos $A$ e $B$ . Em outras palavras, é o tamanho do segmento¹¹endnote: ¹Em aplicações, o comprimento é medido em unidades de comprimento, metro $(m)$ , no sistema internacional de unidades (SI).. Consulte a Figura 1.2

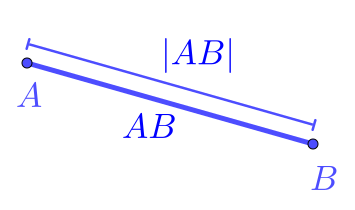
A direção de um segmento $A B$ é a direção de sua reta suporte, i.e. a direção da reta que fica determinada pelos pontos $A$ e $B$ . Logo, dois segmentos $A B$ e $C D$ têm a mesma direção, quando suas retas suportes são paralelas ou coincidentes (ou seja, elas têm a mesma direção).

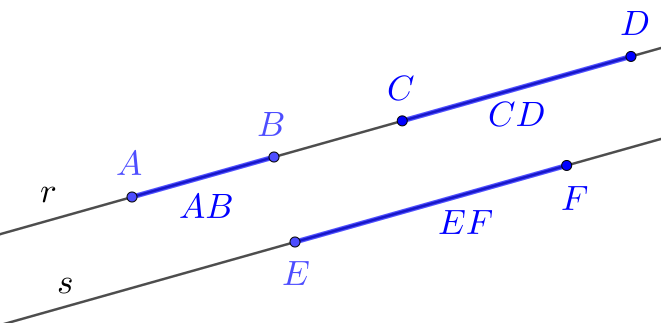
Exemplo 1.1.1.

Consideramos os segmentos representados na Figura 1.4. Observamos que $A B$ e $C D$ têm as mesmas direções, mas comprimentos diferentes. Já, o segmento $E F$ tem o mesmo comprimento que $A B$ (verifique!), mas tem direção diferente dos segmentos $A B$ e $C D$ .

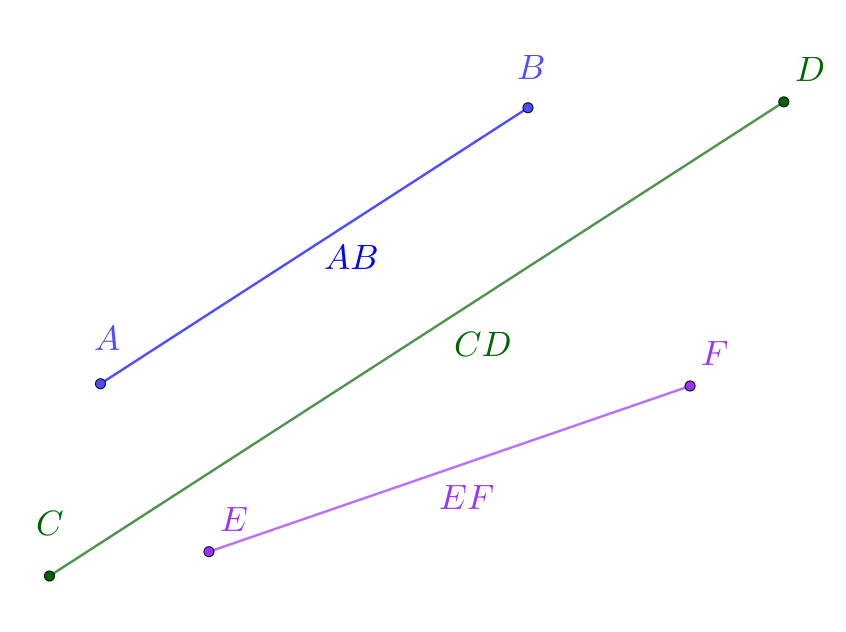
Segmento Nulo

Se $A$ e $B$ são pontos coincidentes, então chamamos $A B$ de segmento nulo e temos $|AB|=0$ . Observamos que a representação geométrica de um segmento nulo é um ponto, tendo em vista que seus pontos extremos são coincidentes. Como existem infinitas retas de diferentes direções que passam por um único ponto, temos que segmentos nulos não têm direção definida.

1.1.2 Segmento Orientado

[[youtube:¡Mv0fW3_6kVg¿]]

Observamos que um dado segmento $A B$ é igual ao segmento $B A$ . Agora, podemos associar a noção de sentido a um segmento, escolhendo um dos pontos como sua origem (ou ponto de partida) e o outro como sua extremidade (ou ponto de chegada). Ao fazermos isso, definimos um segmento orientado.

Mais precisamente, um segmento orientado $\overrightarrow{AB}$ é o segmento definido pelos pontos $A$ e $B$ , sendo $A$ o ponto de partida (origem) e $B$ o ponto de chegada (extremidade). Consulte a Figura 1.5.

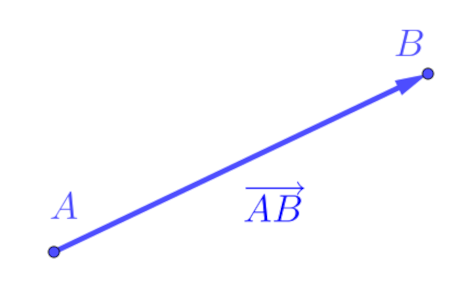
Comprimento e Direção

As noções de comprimento e de direção para segmentos estendem-se diretamente a segmentos orientados. Dizemos que dois segmentos orientados não nulos $\overrightarrow{AB}$ e $\overrightarrow{CD}$ têm a mesma direção, quando as retas $A B$ e $C D$ são paralelas ou coincidentes. Em outras palavras, dois segmentos orientados não nulos têm a mesma direção quando suas retas suporte são paralelas ou coincidentes.

O comprimento de um segmento orientado $\overrightarrow{AB}$ é a norma do segmento $A B$ , i.e. $\left|\overrightarrow{AB}\right|=|AB|$ . O segmento orientado nulo $\overrightarrow{AA}$ tem comprimento $\left|\overrightarrow{AA}\right|=0$ e não tem direção definida.

Sentido

[[youtube:¡nT0VUIp7nIM¿]]

O sentido de um segmento orientado é o do ponto de partida (origem) para o ponto de chegada (extremo). Por exemplo, o segmento orientado $\overrightarrow{AB}$ tem sentido do ponto $A$ ao $B$ .

Segmentos orientados $\overrightarrow{AB}$ e $\overrightarrow{CD}$ de mesma direção podem ter o mesmo sentido ou sentidos opostos. No caso de suas retas suportes não serem coincidentes, os segmentos orientados $\overrightarrow{AB}$ e $\overrightarrow{CD}$ têm o mesmo sentido, quando os segmentos $A C$ e $B D$ não se interceptam. No contrário, caso estes se interceptam, os segmentos orientados $\overrightarrow{AB}$ e $\overrightarrow{CD}$ têm sentidos opostos.

Exemplo 1.1.2.

Na Figura 1.6, temos que os segmentos $\overrightarrow{AB}$ e $\overrightarrow{CD}$ têm o mesmo sentido. De fato, observamos que eles têm a mesma direção e que os segmentos $A C$ e $B D$ têm interseção vazia.

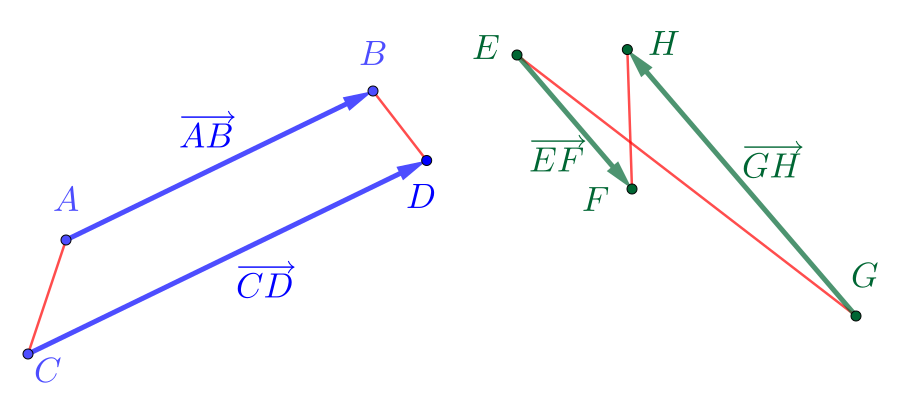
Na mesma Figura 1.6, temos que os segmentos orientados $\overrightarrow{EF}$ e $\overrightarrow{GH}$ têm sentidos opostos, pois têm a mesma direção e os segmentos $E G$ e $F H$ se interceptam.

Observação 1.1.1.

(Transitividade do sentido.) A propriedade de segmentos orientados terem o mesmo sentido é transitiva. Ou seja, se $\overrightarrow{AB}$ e $\overrightarrow{CD}$ têm o mesmo sentido e $\overrightarrow{CD}$ e $\overrightarrow{EF}$ têm o mesmo sentido, então $\overrightarrow{AB}$ e $\overrightarrow{EF}$ têm o mesmo sentido.

Com base na Observação 1.1.1, analisamos o sentido de dois segmentos orientados e colineares escolhendo um deles e construindo um segmento orientado de mesmo sentido e não colinear. Então, analisamos o sentido dos segmentos orientados originais com respeito ao introduzido.

Relação de Equipolência

[[youtube:¡CgfyqqvhBng¿]]

Um segmento orientado não nulo $\overrightarrow{AB}$ é equipolente a um segmento orientado $\overrightarrow{CD}$ , quando $\overrightarrow{AB}$ tem o mesmo comprimento, a mesma direção e o mesmo sentido de $\overrightarrow{CD}$ (consulte a Figura 1.7). Segmentos nulos também são considerados equipolentes entre si.

Usamos a notação $\overrightarrow{AB}\sim\overrightarrow{CD}$ para indicar que $\overrightarrow{AB}$ é equipolente a $\overrightarrow{CD}$ . Caso contrário, escrevemos $\overrightarrow{AB}\not\sim\overrightarrow{CD}$ .

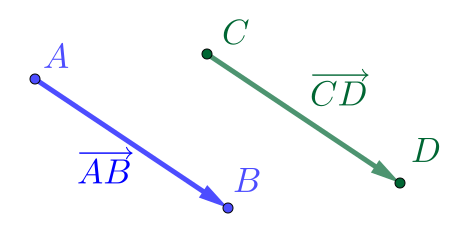
A relação de equipolência é uma relação de equivalência. De fato, temos:

•

relação reflexiva: $\overrightarrow{AB}\sim\overrightarrow{AB}$ ;
•

relação simétrica: $\overrightarrow{AB}\sim\overrightarrow{CD}\Rightarrow\overrightarrow{CD}\sim% \overrightarrow{AB}$ ;
•

relação transitiva: $\overrightarrow{AB}\sim\overrightarrow{CD}\leavevmode\nobreak\ \text{e}% \leavevmode\nobreak\ \overrightarrow{CD}\sim\overrightarrow{EF}\Rightarrow% \overrightarrow{AB}\sim\overrightarrow{EF}$ .

Com isso, dado um segmento orientado $\overrightarrow{AB}$ , definimos a classe de equipolência de $\overrightarrow{AB}$ como o conjunto de todos os seus segmentos equipolentes. O segmento $\overrightarrow{AB}$ é um representante desta classe, a qual é denotada por $\left[\overrightarrow{AB}\right]_{\sim}$ .

1.1.3 Exercícios Resolvidos

ER 1.1.1.

Sejam dados três pontos não colineares $A$ , $B$ e $D$ . Escreva a área do paralelogramo determinado pelos segmentos $A B$ e $A D$ com respeito aos comprimentos deles e ao ângulo determinado por eles.

Solução 0.

Começamos desenhando um paralelogramo determinado por segmentos $A B$ e $A D$ . Consulte a Figura 1.8.

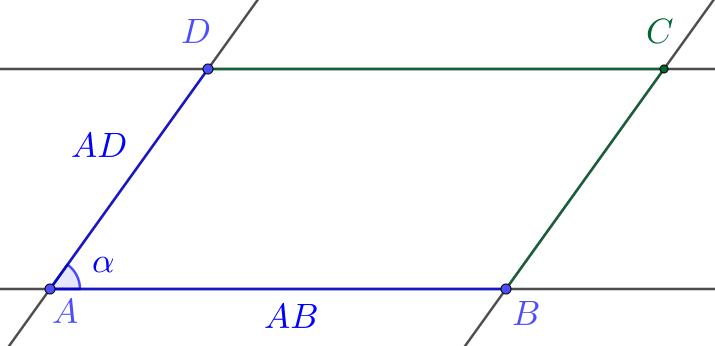
Denotando por $\alpha$ o ângulo determinado pelos segmentos $A B$ e $A D$ , temos que a área deste paralelogramo pode ser escrita por

A=|AB|\cdot|AD|\operatorname{sen}\alpha.

(1.1)

ER 1.1.2.

Mostre que $\overrightarrow{AB}\sim\overrightarrow{CD}$ se, e somente se, $\overrightarrow{BA}\sim\overrightarrow{DC}$ .

Solução 0.

Para mostrar que

\overrightarrow{AB}\sim\overrightarrow{CD}\Leftrightarrow\overrightarrow{BA}% \sim\overrightarrow{DC},

(1.2)

vamos primeiro mostrar a implicação, i.e. que

\overrightarrow{AB}\sim\overrightarrow{CD}\Rightarrow\overrightarrow{BA}\sim% \overrightarrow{DC}.

(1.3)

Logo, assumimos que $\overrightarrow{AB}\sim\overrightarrow{CD}$ , mostramos que

a)

$\left|\overrightarrow{BA}\right|=\left|\overrightarrow{DC}\right|$ .

De fato, temos

$\left|\overrightarrow{BA}\right|=\left|\overrightarrow{AB}\right|\overset{\sim% }{=}\left|\overrightarrow{CD}\right|=\left|\overrightarrow{DC}\right|.$ (1.4)
b)

$\overrightarrow{BA}$ e $\overrightarrow{DC}$ têm as mesmas direções.

A direção de $\overrightarrow{BA}$ é a mesma de $\overrightarrow{AB}$ , pois suas retas suportes são coincidentes. Pela equipolência, essa também é a direção de $\overrightarrow{CD}$ . Por fim, $\overrightarrow{CD}$ e $\overrightarrow{DC}$ têm a mesma direção, pois suas retas suportes são coincidentes. O resultado segue por transitividade.
c)

$\overrightarrow{BA}$ e $\overrightarrow{DC}$ têm os mesmos sentidos.

Como, por hipótese, $\overrightarrow{AB}$ tem o mesmo sentido de $\overrightarrow{CD}$ , temos que os segmentos $A C$ e $B D$ não se interceptam. Isto, por sua vez, mostra que $\overrightarrow{BA}$ e $\overrightarrow{DC}$ têm o mesmo sentido.

Dos items, a), b) e c), concluímos que

\overrightarrow{AB}\sim\overrightarrow{CD}\Rightarrow\overrightarrow{BA}\sim% \overrightarrow{DC}.

(1.5)

Para mostrar a recíproca, i.e. que

\overrightarrow{AB}\sim\overrightarrow{CD}\Leftarrow\overrightarrow{BA}\sim% \overrightarrow{DC}.

(1.6)

basta substituir $\overrightarrow{AB}$ ( $\overrightarrow{BA}$ ) por $\overrightarrow{BA}$ ( $\overrightarrow{AB}$ ) e $\overrightarrow{CD}$ ( $\overrightarrow{DC}$ ) por $\overrightarrow{DC}$ ( $\overrightarrow{CD}$ ) nos itens a), b) e c) demonstrados acima. Em outras palavras, a demonstração é anaĺoga. Verifique!

1.1.4 Exercícios

E. 1.1.1.

Complete as lacunas.

a)

Seja $r$ a reta determinada pelos pontos $A$ e $B$ . O segmento $A B$ é o conjunto de pontos pertencentes a $r$ e que estão entre $A$ e $B$ (inclusive).
b)

O comprimento de um segmento $A B$ é definido como a distância entre $A$ e $B$ e é denotada por —AB—.
c)

Chamamos de reta suporte de um dado segmento $A B$ , a reta determinada pelos pontos $A$ e $B$ .
d)

$A B$ é dito ser um segmento nulo, quando $A$ e $B$ são pontos coincidentes.

Resposta 0.

a) pontos; entre; c) distância; $|AB|$ ; d) reta suporte; e) coincidentes;

E. 1.1.2.

Complete as lacunas.

a)

Segmento orientado é um segmento com sentido definido.
b)

Em um segmento orientado $\overrightarrow{AB}$ , $A$ é chamado de ponto de origem e ponto de extremidade.
c)

Se as retas $A B$ e $C D$ são paralelas ou coincidentes, então $\overrightarrow{AB}$ e $\overrightarrow{CD}$ têm a mesma direção.
d)

O comprimento de um segmento orientado $\overrightarrow{AB}$ é definido como o comprimento do segmento —AB—.
e)

$\overrightarrow{AB}$ e $\overrightarrow{CD}$ têm o mesmo sentido (sentidos opostos) quando os segmentos $A C$ e $B D$ não se interceptam (se interceptam).

Resposta 0.

a) sentido; b) ponto de origem; ponto de extremidade; c) direção; d) $|AB|$ ; e) o mesmo sentido (sentidos opostos); não se interceptam (se interceptam)

E. 1.1.3.

Complete as lacunas.

a)

$\overrightarrow{AB}$ e $\overrightarrow{CD}$ são equipolentes se, e somente se, $\overrightarrow{AB}$ e $\overrightarrow{CD}$ têm a mesma direção, o mesmo comprimento e o mesmo sentido.
b)

Pela reflexividade da relação de equipolência, $\overrightarrow{CD}\sim$ $\overrightarrow{CD}$ .
c)

Pela simetria da relação de equipolência, se $\overrightarrow{EF}\sim\overrightarrow{AB}$ , então $\overrightarrow{AB}\sim\overrightarrow{EF}$ .
d)

Pela transitividade da relação de equipolência, se $\overrightarrow{CD}\sim\overrightarrow{AB}$ e $\overrightarrow{AB}\sim\overrightarrow{EF}$ , então $\overrightarrow{CD}\sim\overrightarrow{EF}$ .

Resposta 0.

a) equipolentes; direção; comprimento; sentido; b) $\overrightarrow{CD}$ ; c) $\overrightarrow{AB}\sim\overrightarrow{EF}$ ; d) $\overrightarrow{AB}\sim\overrightarrow{EF}$

E. 1.1.4.

Faça o esboço de dois segmentos $A B$ e $C D$ com $|AB|\neq|CD|$ e cujas retas determinadas por eles sejam coincidentes.

Resposta 0.

E. 1.1.5.

Faça o esboço de dois segmentos orientados $AB\not\sim CD$ e de mesmo sentido.

Resposta 0.

E. 1.1.6.

Faça o esboço de dois segmentos orientados colineares, de comprimentos iguais e sentidos opostos.

Resposta 0.

E. 1.1.7.

Mostre que segmentos terem o mesmo comprimento é uma:

a)

relação reflexiva.
b)

relação simétrica.
c)

relação transitiva.
d)

relação de equivalência.

Resposta 0.

a) Por óbvio, que $A B$ tem o mesmo comprimento que si próprio. b) Se $A B$ tem o mesmo comprimento de $C D$ , $|AB|=|CD|$ , então é dizer que $C D$ tem o mesmo comprimento de $A B$ . c) Se $|AB|=|CD|$ e $|CD|=|EF|$ , então $|AB|=|EF|$ . d) Por definição, segue dos itens $a)$ , $b)$ e $c)$ .

E. 1.1.8.

Mostre que $\overrightarrow{AB}\sim\overrightarrow{CD}$ , então $\overrightarrow{AC}\sim\overrightarrow{BD}$ .

Resposta 0.

Dica: Se $\overrightarrow{AB}$ e $\overrightarrow{CD}$ não são coincidentes, então $A B C D$ determina um paralelogramo.

E. 1.1.9.

Mostre que se $AC\sim CB$ , então $C$ é ponto médio do segmento $A B$ .

Resposta 0.

$AC\sim CB$ implica que $C\in AB$ . Como $\left|\overrightarrow{AC}\right|=\left|\overrightarrow{CB}\right|$ , conclui-se que $C$ é o ponto médio de $A B$ .

E. 1.1.10.

Mostre que se $\overrightarrow{AB}$ e $\overrightarrow{CD}$ são equipolentes, então os pontos médios de $A D$ e $B C$ são coincidentes.

Resposta 0.

Dica: as diagonais de um paralelogramo interceptam-se em seus pontos médios.

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Vetores

1 Fundamentos 1 Fundamentos 1.2 Definição de Vetor

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

1.1 Segmentos Orientados

1.1.1 Segmento

[[youtube:¡J-GN-uulfRs¿]]

Comprimento e Direção

Exemplo 1.1.1.

Segmento Nulo

1.1.2 Segmento Orientado

[[youtube:¡Mv0fW3_6kVg¿]]

Comprimento e Direção

Sentido

[[youtube:¡nT0VUIp7nIM¿]]

O sentido de um segmento orientado é o do ponto de partida (origem) para o ponto de chegada (extremo). Por exemplo, o segmento orientado $\overrightarrow{AB}$ tem sentido do ponto $A$ ao $B$ .

Exemplo 1.1.2.

Na mesma Figura 1.6, temos que os segmentos orientados $\overrightarrow{EF}$ e $\overrightarrow{GH}$ têm sentidos opostos, pois têm a mesma direção e os segmentos $E G$ e $F H$ se interceptam.

Observação 1.1.1.

Relação de Equipolência

[[youtube:¡CgfyqqvhBng¿]]

A relação de equipolência é uma relação de equivalência. De fato, temos:

•

relação reflexiva: $\overrightarrow{AB}\sim\overrightarrow{AB}$ ;
•

relação simétrica: $\overrightarrow{AB}\sim\overrightarrow{CD}\Rightarrow\overrightarrow{CD}\sim% \overrightarrow{AB}$ ;
•

relação transitiva: $\overrightarrow{AB}\sim\overrightarrow{CD}\leavevmode\nobreak\ \text{e}% \leavevmode\nobreak\ \overrightarrow{CD}\sim\overrightarrow{EF}\Rightarrow% \overrightarrow{AB}\sim\overrightarrow{EF}$ .

1.1.3 Exercícios Resolvidos

ER 1.1.1.

Solução 0.

Começamos desenhando um paralelogramo determinado por segmentos $A B$ e $A D$ . Consulte a Figura 1.8.

Denotando por $\alpha$ o ângulo determinado pelos segmentos $A B$ e $A D$ , temos que a área deste paralelogramo pode ser escrita por

A=|AB|\cdot|AD|\operatorname{sen}\alpha.

(1.1)

ER 1.1.2.

Mostre que $\overrightarrow{AB}\sim\overrightarrow{CD}$ se, e somente se, $\overrightarrow{BA}\sim\overrightarrow{DC}$ .

Solução 0.

Para mostrar que

\overrightarrow{AB}\sim\overrightarrow{CD}\Leftrightarrow\overrightarrow{BA}% \sim\overrightarrow{DC},

(1.2)

vamos primeiro mostrar a implicação, i.e. que

\overrightarrow{AB}\sim\overrightarrow{CD}\Rightarrow\overrightarrow{BA}\sim% \overrightarrow{DC}.

(1.3)

Logo, assumimos que $\overrightarrow{AB}\sim\overrightarrow{CD}$ , mostramos que

a)

$\left|\overrightarrow{BA}\right|=\left|\overrightarrow{DC}\right|$ .

De fato, temos

$\left|\overrightarrow{BA}\right|=\left|\overrightarrow{AB}\right|\overset{\sim% }{=}\left|\overrightarrow{CD}\right|=\left|\overrightarrow{DC}\right|.$ (1.4)
b)

$\overrightarrow{BA}$ e $\overrightarrow{DC}$ têm as mesmas direções.

A direção de $\overrightarrow{BA}$ é a mesma de $\overrightarrow{AB}$ , pois suas retas suportes são coincidentes. Pela equipolência, essa também é a direção de $\overrightarrow{CD}$ . Por fim, $\overrightarrow{CD}$ e $\overrightarrow{DC}$ têm a mesma direção, pois suas retas suportes são coincidentes. O resultado segue por transitividade.
c)

$\overrightarrow{BA}$ e $\overrightarrow{DC}$ têm os mesmos sentidos.

Como, por hipótese, $\overrightarrow{AB}$ tem o mesmo sentido de $\overrightarrow{CD}$ , temos que os segmentos $A C$ e $B D$ não se interceptam. Isto, por sua vez, mostra que $\overrightarrow{BA}$ e $\overrightarrow{DC}$ têm o mesmo sentido.

Dos items, a), b) e c), concluímos que

\overrightarrow{AB}\sim\overrightarrow{CD}\Rightarrow\overrightarrow{BA}\sim% \overrightarrow{DC}.

(1.5)

Para mostrar a recíproca, i.e. que

\overrightarrow{AB}\sim\overrightarrow{CD}\Leftarrow\overrightarrow{BA}\sim% \overrightarrow{DC}.

(1.6)

1.1.4 Exercícios

E. 1.1.1.

Complete as lacunas.

a)

Seja $r$ a reta determinada pelos pontos $A$ e $B$ . O segmento $A B$ é o conjunto de pontos pertencentes a $r$ e que estão entre $A$ e $B$ (inclusive).
b)

O comprimento de um segmento $A B$ é definido como a distância entre $A$ e $B$ e é denotada por —AB—.
c)

Chamamos de reta suporte de um dado segmento $A B$ , a reta determinada pelos pontos $A$ e $B$ .
d)

$A B$ é dito ser um segmento nulo, quando $A$ e $B$ são pontos coincidentes.

Resposta 0.

a) pontos; entre; c) distância; $|AB|$ ; d) reta suporte; e) coincidentes;

E. 1.1.2.

Complete as lacunas.

a)

Segmento orientado é um segmento com sentido definido.
b)

Em um segmento orientado $\overrightarrow{AB}$ , $A$ é chamado de ponto de origem e ponto de extremidade.
c)

Se as retas $A B$ e $C D$ são paralelas ou coincidentes, então $\overrightarrow{AB}$ e $\overrightarrow{CD}$ têm a mesma direção.
d)

O comprimento de um segmento orientado $\overrightarrow{AB}$ é definido como o comprimento do segmento —AB—.
e)

$\overrightarrow{AB}$ e $\overrightarrow{CD}$ têm o mesmo sentido (sentidos opostos) quando os segmentos $A C$ e $B D$ não se interceptam (se interceptam).

Resposta 0.

a) sentido; b) ponto de origem; ponto de extremidade; c) direção; d) $|AB|$ ; e) o mesmo sentido (sentidos opostos); não se interceptam (se interceptam)

E. 1.1.3.

Complete as lacunas.

a)

$\overrightarrow{AB}$ e $\overrightarrow{CD}$ são equipolentes se, e somente se, $\overrightarrow{AB}$ e $\overrightarrow{CD}$ têm a mesma direção, o mesmo comprimento e o mesmo sentido.
b)

Pela reflexividade da relação de equipolência, $\overrightarrow{CD}\sim$ $\overrightarrow{CD}$ .
c)

Pela simetria da relação de equipolência, se $\overrightarrow{EF}\sim\overrightarrow{AB}$ , então $\overrightarrow{AB}\sim\overrightarrow{EF}$ .
d)

Pela transitividade da relação de equipolência, se $\overrightarrow{CD}\sim\overrightarrow{AB}$ e $\overrightarrow{AB}\sim\overrightarrow{EF}$ , então $\overrightarrow{CD}\sim\overrightarrow{EF}$ .

Resposta 0.

a) equipolentes; direção; comprimento; sentido; b) $\overrightarrow{CD}$ ; c) $\overrightarrow{AB}\sim\overrightarrow{EF}$ ; d) $\overrightarrow{AB}\sim\overrightarrow{EF}$

E. 1.1.4.

Faça o esboço de dois segmentos $A B$ e $C D$ com $|AB|\neq|CD|$ e cujas retas determinadas por eles sejam coincidentes.

Resposta 0.

E. 1.1.5.

Faça o esboço de dois segmentos orientados $AB\not\sim CD$ e de mesmo sentido.

Resposta 0.

E. 1.1.6.

Faça o esboço de dois segmentos orientados colineares, de comprimentos iguais e sentidos opostos.

Resposta 0.

E. 1.1.7.

Mostre que segmentos terem o mesmo comprimento é uma:

a)

relação reflexiva.
b)

relação simétrica.
c)

relação transitiva.
d)

relação de equivalência.

Resposta 0.

E. 1.1.8.

Mostre que $\overrightarrow{AB}\sim\overrightarrow{CD}$ , então $\overrightarrow{AC}\sim\overrightarrow{BD}$ .

Resposta 0.

Dica: Se $\overrightarrow{AB}$ e $\overrightarrow{CD}$ não são coincidentes, então $A B C D$ determina um paralelogramo.

E. 1.1.9.

Mostre que se $AC\sim CB$ , então $C$ é ponto médio do segmento $A B$ .

Resposta 0.

$AC\sim CB$ implica que $C\in AB$ . Como $\left|\overrightarrow{AC}\right|=\left|\overrightarrow{CB}\right|$ , conclui-se que $C$ é o ponto médio de $A B$ .

E. 1.1.10.

Mostre que se $\overrightarrow{AB}$ e $\overrightarrow{CD}$ são equipolentes, então os pontos médios de $A D$ e $B C$ são coincidentes.

Resposta 0.

Dica: as diagonais de um paralelogramo interceptam-se em seus pontos médios.

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Pedro H A Konzen

| | | |