Política de uso de dados

Ao navegar por este site, você concorda com a política de uso de dados.

Política de uso de dados

Ao navegar por este site, você concorda com a política de uso de dados.

| | | |

Redes Neurais Artificiais

4 Redes Informadas pela Física 4.2 Aplicação: Equação do Calor 4.4 Integração de Funções

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

4.3 PINN com Parâmetro a Determinar

Em construção

Vamos considerar uma equação diferencial

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}L(u;\lambda)=f% ,\leavevmode\nobreak\ \boldsymbol{x}\in D\subset\mathbb{R}^{n},

(4.13)

onde $L$ é um operador em funções $u=u(\boldsymbol{x})$ , $\lambda\in\mathbb{R}$ é um parâmetro a determinar e $f$ uma dada função fonte. Assumimos conhecidas condições inicial e de contorno, bem como um conjunto de amostras

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\mathcal{D}:=% \left\{\left(\boldsymbol{x}^{(s)},u^{(s)}\right)\right\}_{s=1}^{n_{s}},

(4.14)

com $\boldsymbol{x}^{(s)}\in D$ e $u^{(s)}=u\left(\boldsymbol{x}^{(s)}\right)$ .

Uma rede informada pela física (PINN, do inglês, Physics-informed neural network) com parâmetro a determinar é uma rede neural

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\tilde{u}=% \mathcal{N}(\boldsymbol{x};\lambda),

(4.15)

em que $\tilde{u}$ é a solução estimada do modelo dado pela equação diferencial (4.13) com dadas condições inicial e de contorno, em que o parâmetro $\lambda$ é estimado tal que

\tilde{u}^{(s)}\approx u^{(s)},\leavevmode\nobreak\ \left(\boldsymbol{x}^{(s)}% ,u^{(s)}\right)\in\mathcal{D}.

(4.16)

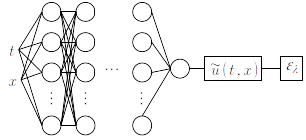
Refer to caption — Figura 4.2: Esquema de uma PINN $\tilde{u}=\mathcal{N}(\boldsymbol{x};\lambda)$ .

Considerando uma rede do tipo perceptron multicamadas (MLP, do inglês, multilayer perceptron, consulte Fig. 4.2), seus pesos e biases são treinados em conjunto com parâmetro $\lambda$ de forma a minimizar a função de perda

		$\displaystyle{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1% }\pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\varepsilon_{% \lambda}:=\underbrace{\frac{1}{n_{\text{in}}}\sum_{s=1}^{n_{\text{in}}}\left\|% \mathcal{R}_{\lambda}\left(\boldsymbol{x}_{\text{in}}^{(s)}\right)\right\|^{2}}% _{\text{pts. internos}}}$		(4.17)
		$\displaystyle{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1% }\pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\quad+% \underbrace{\frac{1}{n_{\text{cc}}}\sum_{s=1}^{n_{\text{cc}}}\left\|\tilde{u}_{% \text{cc}}-u_{\text{cc}}\right\|^{2}}_{\text{c.i. \& c.c.}}}$
		$\displaystyle{\color[rgb]{1,0,0}\definecolor[named]{pgfstrokecolor}{rgb}{1,0,0% }\pgfsys@color@rgb@stroke{1}{0}{0}\pgfsys@color@rgb@fill{1}{0}{0}\quad+% \underbrace{\frac{p}{n_{s}}\sum_{s=1}^{n_{s}}\left\|\tilde{u}^{(s)}-u^{(s)}% \right\|^{2}}_{\text{amostras}}},$

onde $p\geq 0$ é uma penalidade e

\mathcal{R}_{\lambda}(\boldsymbol{x}):=f-L(u;\lambda)

(4.18)

é o resíduo de (4.13).

Exemplo 4.3.1.

Consideramos a equação de Fisher¹³¹³endnote: ¹³Ronald Aylmer Fisher, 1890-1962, biólogo inglês. Fonte: Wikipédia: Ronald Fisher.

u_{t}=u_{xx}+\lambda u(1-u),\leavevmode\nobreak\ (t,x)\in(0,t_{f})\times(0,1),

(4.19)

com o parâmetro $\lambda>0$ a determinar. Assumimos dadas condição inicial

u(0,x)=\frac{1}{\left(1+e^{\sqrt{\frac{\lambda}{6}}x}\right)^{2}},\leavevmode% \nobreak\ x\in[0,1],

(4.20)

e condições de contorno

	$\displaystyle u_{x}(t,0)=\frac{1}{\left(1+e^{-\frac{5}{6}\lambda t}\right)^{2}},$		(4.21)
	$\displaystyle u_{x}(t,0)=\frac{1}{\left(1+e^{\sqrt{\frac{\lambda}{6}}-\frac{5}% {6}\lambda t}\right)^{2}}.$		(4.22)

Este problema tem solução analítica [AÖ10]

u_{a}(t,x)=\frac{1}{\left(1+e^{\sqrt{\frac{\lambda}{6}}x-\frac{5}{6}\lambda t}% \right)^{2}}.

(4.23)

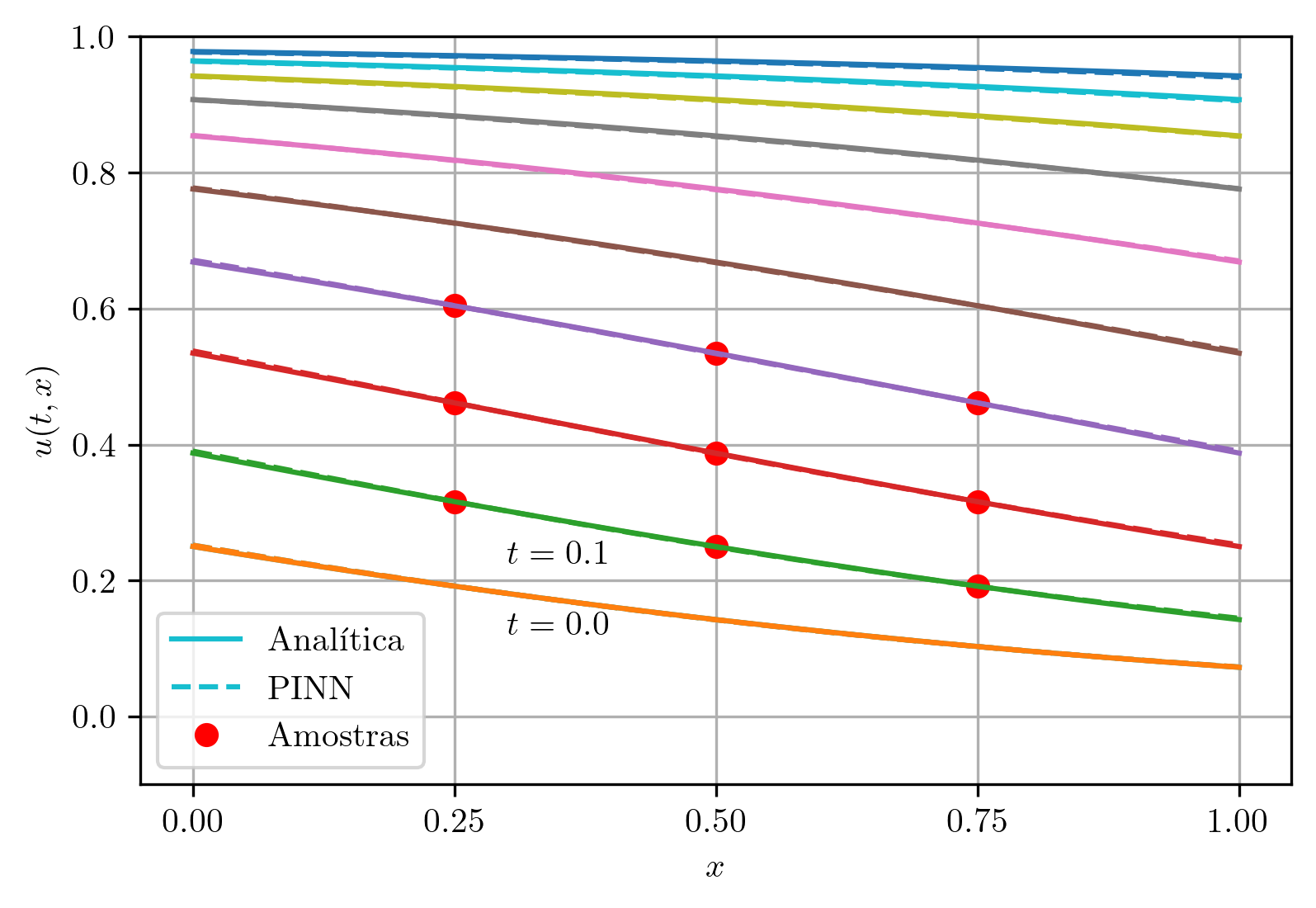
Como exemplo de aplicação de uma PINN com parâmetro a determinar, vamos assumir o seguinte conjunto de amostras

\mathcal{D}=\left\{\left(\left(t^{(s)},x^{(s)}\right),u^{(s)}\right)\right\}_{% s=1}^{n_{s}},

(4.24)

com $\left(t^{(s)},x^{(s)}\right)\in\{0.1,0.2,0.3\}\times\{0.25,0.5,0.75\}$ e $u^{(s)}=u_{a}\left(t^{(s)},x^{(s)}\right)$ .

Código 15: ex_pinn_fisher.py

⬇

1import torch

3# modelo

4nh = 4

5nn = 50

6fun = torch.nn.Tanh()

7model = torch.nn.Sequential()

8model.add_module('layer_1', torch.nn.Linear(2, nn))

9model.add_module('fun_1', fun)

10for l in range(2, nh+1):

11 model.add_module(f'layer_{l}', torch.nn.Linear(nn, nn))

12 model.add_module(f'fun_{l}', fun)

13model.add_module(f'layer_{nh+1}', torch.nn.Linear(nn, 1))

15# parâmetro

16rgn = [5., 7]

17model.lmbda = torch.nn.Parameter(

18 data=(rgn[1]-rgn[0])*torch.rand(1)+rgn[0])

20# otimizador

21optim = torch.optim.Adam(model.parameters(), lr=0.001)

23# parâmetros do problema

24tf = 1.

26# solução analítica

27lmbda = torch.tensor([6.])

28def ua(t,x, lmbda=lmbda):

29 return 1./(1.+torch.exp(torch.sqrt(lmbda/6.)*x-5./6*lmbda*t))**2

31# condição inicial

32def u0(x, lmbda=lmbda):

33 return 1./(1.+torch.exp(torch.sqrt(lmbda/6)*x))**2

35# amostras

36ts = torch.tensor([0.1, 0.2, 0.3])

37xs = torch.tensor([0.25, 0.5, 0.75])

38T, X = torch.meshgrid(ts, xs, indexing='ij')

39Ss = torch.hstack((T.reshape(-1,1), X.reshape(-1,1)))

40Us_exp = ua(T, X).reshape(-1,1)

42# treinamento

43nepochs = 50000

44tol = 1e-5

46eout = 100

48sin = 50

49penalty = 1e1

51for epoch in range(nepochs):

53 # forward

55 ## pts internos

56 tsin = tf*torch.rand(sin, 1)

57 xsin = torch.rand(sin, 1)

58 Sin = torch.hstack((tsin, xsin))

59 Sin.requires_grad = True

61 Uin = model(Sin)

63 ## loss pts internos

64 DUin = torch.autograd.grad(

65 Uin, Sin,

66 torch.ones_like(Uin),

67 create_graph=True,

68 retain_graph=True)[0]

69 Uin_t = DUin[:,0:1]

70 Uin_x = DUin[:,1:2]

72 Uin_xx = torch.autograd.grad(

73 Uin_x, Sin,

74 torch.ones_like(Uin_x),

75 create_graph=True,

76 retain_graph=True)[0][:,1:2]

79 lin = torch.mean((Uin_t - Uin_xx \

80 - model.lmbda*Uin*(1-Uin))**2)

82 ## cond. inicial

83 S0 = torch.hstack((torch.zeros_like(xsin), xsin))

85 U0 = model(S0)

87 ## loss cond. inicial

88 l0 = torch.mean((U0 - u0(xsin))**2)

90 ## cond. de contorno

91 Sbc0 = torch.hstack((tsin, torch.zeros_like(xsin)))

92 Sbc1 = torch.hstack((tsin, torch.ones_like(xsin)))

93 Sbc = torch.vstack((Sbc0, Sbc1))

95 Ubc_exp = ua(Sbc[:,0:1],Sbc[:,1:2])

96 Ubc_est = model(Sbc)

98 ## loss cond. de contorno

99 lbc = torch.mean((Ubc_est - Ubc_exp)**2)

100

101 ## amostras

102 Us_est = model(Ss)

103

104 ## loss amostras

105 ls = torch.mean((Us_est - Us_exp)**2)

106

107 ## loss total

108 loss = lin + l0 + lbc + penalty*ls

109

110 if ((epoch % eout == 0) or (loss.item() < tol)):

111 print(f'epoch: {epoch}, '\

112 + f'loss={loss.item():.4e}, '\

113 + f'lmbda={model.lmbda.item():.3f}')

114

115 if (loss.item() < tol):

116 break

117

118 optim.zero_grad()

119 loss.backward()

120 optim.step()

4.3.1 Exercícios

Em construção

Exemplo 4.3.2.

Considere o seguinte problema de valor inicial

	$\displaystyle-u^{\prime\prime}=\lambda\operatorname{sen}(\pi x),\leavevmode% \nobreak\ 0<x<1,$		(4.25a)
	$\displaystyle u(0)=u(1)=0,$		(4.25b)

onde $\lambda>0$ é um parâmetro a determinar. Dadas as amostras

\mathcal{D}=\left\{\left(\frac{1}{6},\frac{1}{2}\right),\left(\frac{1}{4},% \sqrt{2}{2}\right),\left(\frac{1}{3},\sqrt{3}{3}\right)\right\},

(4.26)

crie uma PINN

\tilde{u}=\mathcal{N}(x;\lambda)

(4.27)

para estimar o parâmetro $\lambda$ e a solução em todo o domínio $0\leq x\leq 1$ .

Resposta.

$\lambda=\pi^{2}$

Exemplo 4.3.3.

Considere o problema de Poisson¹⁴¹⁴endnote: ¹⁴Siméon Denis Poisson, 1781 - 1840, matemático francês. Fonte: Wikipédia:Siméon Denis Poisson.

	$\displaystyle-\nabla u=\lambda,\leavevmode\nobreak\ (x,y)\in D=(-1,1)^{2},$		(4.28a)
	$\displaystyle u=0,(x,y)\in\partial D,$		(4.28b)

onde $\lambda>0$ é um parâmetro a determinar. Dado que $u(1/2,1/2)=1/8$ , crie uma PINN

\tilde{u}=\mathcal{N}(x,y;\lambda)

(4.29)

para estimar o parâmetro $\lambda$ e a solução em todo o domínio $D$ .

Resposta.

$\lambda=1$

Exemplo 4.3.4.

Considere o problema de calor

	$\displaystyle u_{t}=\lambda u_{xx}+(\pi^{2}-1)e^{-t}\operatorname{sen}(\pi x),% \leavevmode\nobreak\ (t,x)\in(0,1)^{2},$		(4.30a)
	$\displaystyle u(0,x)=\operatorname{sen}(\pi x),\leavevmode\nobreak\ x\in[0,1],$		(4.30b)
	$\displaystyle u(t,0)=u(t,1)=0,\leavevmode\nobreak\ t\in[0,1],$		(4.30c)

onde o coeficiente de difusão $\lambda>0$ é um parâmetro a determinar. Sabendo que o problema tem solução analítica

u(t,x)=e^{-t}\operatorname{sen}(\pi x),

(4.31)

escolha um conjunto de amostras $\mathcal{D}=\left\{\left(\left(t^{(s)},x^{(s)}\right),u^{(s)}\right)\right\}_{% s=1}^{n_{s}}$ tal que seja possível estimar $\lambda$ com uma PINN

\tilde{u}=\mathcal{N}(t,x;\lambda).

(4.32)

Resposta.

$\lambda=1$

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Redes Neurais Artificiais

4 Redes Informadas pela Física 4.2 Aplicação: Equação do Calor 4.4 Integração de Funções

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

4.3 PINN com Parâmetro a Determinar

Em construção

Vamos considerar uma equação diferencial

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}L(u;\lambda)=f% ,\leavevmode\nobreak\ \boldsymbol{x}\in D\subset\mathbb{R}^{n},

(4.13)

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\mathcal{D}:=% \left\{\left(\boldsymbol{x}^{(s)},u^{(s)}\right)\right\}_{s=1}^{n_{s}},

(4.14)

com $\boldsymbol{x}^{(s)}\in D$ e $u^{(s)}=u\left(\boldsymbol{x}^{(s)}\right)$ .

Uma rede informada pela física (PINN, do inglês, Physics-informed neural network) com parâmetro a determinar é uma rede neural

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\tilde{u}=% \mathcal{N}(\boldsymbol{x};\lambda),

(4.15)

em que $\tilde{u}$ é a solução estimada do modelo dado pela equação diferencial (4.13) com dadas condições inicial e de contorno, em que o parâmetro $\lambda$ é estimado tal que

\tilde{u}^{(s)}\approx u^{(s)},\leavevmode\nobreak\ \left(\boldsymbol{x}^{(s)}% ,u^{(s)}\right)\in\mathcal{D}.

(4.16)

		$\displaystyle{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1% }\pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\varepsilon_{% \lambda}:=\underbrace{\frac{1}{n_{\text{in}}}\sum_{s=1}^{n_{\text{in}}}\left\|% \mathcal{R}_{\lambda}\left(\boldsymbol{x}_{\text{in}}^{(s)}\right)\right\|^{2}}% _{\text{pts. internos}}}$		(4.17)
		$\displaystyle{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1% }\pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\quad+% \underbrace{\frac{1}{n_{\text{cc}}}\sum_{s=1}^{n_{\text{cc}}}\left\|\tilde{u}_{% \text{cc}}-u_{\text{cc}}\right\|^{2}}_{\text{c.i. \& c.c.}}}$
		$\displaystyle{\color[rgb]{1,0,0}\definecolor[named]{pgfstrokecolor}{rgb}{1,0,0% }\pgfsys@color@rgb@stroke{1}{0}{0}\pgfsys@color@rgb@fill{1}{0}{0}\quad+% \underbrace{\frac{p}{n_{s}}\sum_{s=1}^{n_{s}}\left\|\tilde{u}^{(s)}-u^{(s)}% \right\|^{2}}_{\text{amostras}}},$

onde $p\geq 0$ é uma penalidade e

\mathcal{R}_{\lambda}(\boldsymbol{x}):=f-L(u;\lambda)

(4.18)

é o resíduo de (4.13).

Exemplo 4.3.1.

Consideramos a equação de Fisher¹³¹³endnote: ¹³Ronald Aylmer Fisher, 1890-1962, biólogo inglês. Fonte: Wikipédia: Ronald Fisher.

u_{t}=u_{xx}+\lambda u(1-u),\leavevmode\nobreak\ (t,x)\in(0,t_{f})\times(0,1),

(4.19)

com o parâmetro $\lambda>0$ a determinar. Assumimos dadas condição inicial

u(0,x)=\frac{1}{\left(1+e^{\sqrt{\frac{\lambda}{6}}x}\right)^{2}},\leavevmode% \nobreak\ x\in[0,1],

(4.20)

e condições de contorno

	$\displaystyle u_{x}(t,0)=\frac{1}{\left(1+e^{-\frac{5}{6}\lambda t}\right)^{2}},$		(4.21)
	$\displaystyle u_{x}(t,0)=\frac{1}{\left(1+e^{\sqrt{\frac{\lambda}{6}}-\frac{5}% {6}\lambda t}\right)^{2}}.$		(4.22)

Este problema tem solução analítica [AÖ10]

u_{a}(t,x)=\frac{1}{\left(1+e^{\sqrt{\frac{\lambda}{6}}x-\frac{5}{6}\lambda t}% \right)^{2}}.

(4.23)

Como exemplo de aplicação de uma PINN com parâmetro a determinar, vamos assumir o seguinte conjunto de amostras

\mathcal{D}=\left\{\left(\left(t^{(s)},x^{(s)}\right),u^{(s)}\right)\right\}_{% s=1}^{n_{s}},

(4.24)

com $\left(t^{(s)},x^{(s)}\right)\in\{0.1,0.2,0.3\}\times\{0.25,0.5,0.75\}$ e $u^{(s)}=u_{a}\left(t^{(s)},x^{(s)}\right)$ .

Código 15: ex_pinn_fisher.py

⬇

1import torch

3# modelo

4nh = 4

5nn = 50

6fun = torch.nn.Tanh()

7model = torch.nn.Sequential()

8model.add_module('layer_1', torch.nn.Linear(2, nn))

9model.add_module('fun_1', fun)

10for l in range(2, nh+1):

11 model.add_module(f'layer_{l}', torch.nn.Linear(nn, nn))

12 model.add_module(f'fun_{l}', fun)

13model.add_module(f'layer_{nh+1}', torch.nn.Linear(nn, 1))

15# parâmetro

16rgn = [5., 7]

17model.lmbda = torch.nn.Parameter(

18 data=(rgn[1]-rgn[0])*torch.rand(1)+rgn[0])

20# otimizador

21optim = torch.optim.Adam(model.parameters(), lr=0.001)

23# parâmetros do problema

24tf = 1.

26# solução analítica

27lmbda = torch.tensor([6.])

28def ua(t,x, lmbda=lmbda):

29 return 1./(1.+torch.exp(torch.sqrt(lmbda/6.)*x-5./6*lmbda*t))**2

31# condição inicial

32def u0(x, lmbda=lmbda):

33 return 1./(1.+torch.exp(torch.sqrt(lmbda/6)*x))**2

35# amostras

36ts = torch.tensor([0.1, 0.2, 0.3])

37xs = torch.tensor([0.25, 0.5, 0.75])

38T, X = torch.meshgrid(ts, xs, indexing='ij')

39Ss = torch.hstack((T.reshape(-1,1), X.reshape(-1,1)))

40Us_exp = ua(T, X).reshape(-1,1)

42# treinamento

43nepochs = 50000

44tol = 1e-5

46eout = 100

48sin = 50

49penalty = 1e1

51for epoch in range(nepochs):

53 # forward

55 ## pts internos

56 tsin = tf*torch.rand(sin, 1)

57 xsin = torch.rand(sin, 1)

58 Sin = torch.hstack((tsin, xsin))

59 Sin.requires_grad = True

61 Uin = model(Sin)

63 ## loss pts internos

64 DUin = torch.autograd.grad(

65 Uin, Sin,

66 torch.ones_like(Uin),

67 create_graph=True,

68 retain_graph=True)[0]

69 Uin_t = DUin[:,0:1]

70 Uin_x = DUin[:,1:2]

72 Uin_xx = torch.autograd.grad(

73 Uin_x, Sin,

74 torch.ones_like(Uin_x),

75 create_graph=True,

76 retain_graph=True)[0][:,1:2]

79 lin = torch.mean((Uin_t - Uin_xx \

80 - model.lmbda*Uin*(1-Uin))**2)

82 ## cond. inicial

83 S0 = torch.hstack((torch.zeros_like(xsin), xsin))

85 U0 = model(S0)

87 ## loss cond. inicial

88 l0 = torch.mean((U0 - u0(xsin))**2)

90 ## cond. de contorno

91 Sbc0 = torch.hstack((tsin, torch.zeros_like(xsin)))

92 Sbc1 = torch.hstack((tsin, torch.ones_like(xsin)))

93 Sbc = torch.vstack((Sbc0, Sbc1))

95 Ubc_exp = ua(Sbc[:,0:1],Sbc[:,1:2])

96 Ubc_est = model(Sbc)

98 ## loss cond. de contorno

99 lbc = torch.mean((Ubc_est - Ubc_exp)**2)

100

101 ## amostras

102 Us_est = model(Ss)

103

104 ## loss amostras

105 ls = torch.mean((Us_est - Us_exp)**2)

106

107 ## loss total

108 loss = lin + l0 + lbc + penalty*ls

109

110 if ((epoch % eout == 0) or (loss.item() < tol)):

111 print(f'epoch: {epoch}, '\

112 + f'loss={loss.item():.4e}, '\

113 + f'lmbda={model.lmbda.item():.3f}')

114

115 if (loss.item() < tol):

116 break

117

118 optim.zero_grad()

119 loss.backward()

120 optim.step()

4.3.1 Exercícios

Em construção

Exemplo 4.3.2.

Considere o seguinte problema de valor inicial

	$\displaystyle-u^{\prime\prime}=\lambda\operatorname{sen}(\pi x),\leavevmode% \nobreak\ 0<x<1,$		(4.25a)
	$\displaystyle u(0)=u(1)=0,$		(4.25b)

onde $\lambda>0$ é um parâmetro a determinar. Dadas as amostras

\mathcal{D}=\left\{\left(\frac{1}{6},\frac{1}{2}\right),\left(\frac{1}{4},% \sqrt{2}{2}\right),\left(\frac{1}{3},\sqrt{3}{3}\right)\right\},

(4.26)

crie uma PINN

\tilde{u}=\mathcal{N}(x;\lambda)

(4.27)

para estimar o parâmetro $\lambda$ e a solução em todo o domínio $0\leq x\leq 1$ .

Resposta.

$\lambda=\pi^{2}$

Exemplo 4.3.3.

Considere o problema de Poisson¹⁴¹⁴endnote: ¹⁴Siméon Denis Poisson, 1781 - 1840, matemático francês. Fonte: Wikipédia:Siméon Denis Poisson.

	$\displaystyle-\nabla u=\lambda,\leavevmode\nobreak\ (x,y)\in D=(-1,1)^{2},$		(4.28a)
	$\displaystyle u=0,(x,y)\in\partial D,$		(4.28b)

onde $\lambda>0$ é um parâmetro a determinar. Dado que $u(1/2,1/2)=1/8$ , crie uma PINN

\tilde{u}=\mathcal{N}(x,y;\lambda)

(4.29)

para estimar o parâmetro $\lambda$ e a solução em todo o domínio $D$ .

Resposta.

$\lambda=1$

Exemplo 4.3.4.

Considere o problema de calor

	$\displaystyle u_{t}=\lambda u_{xx}+(\pi^{2}-1)e^{-t}\operatorname{sen}(\pi x),% \leavevmode\nobreak\ (t,x)\in(0,1)^{2},$		(4.30a)
	$\displaystyle u(0,x)=\operatorname{sen}(\pi x),\leavevmode\nobreak\ x\in[0,1],$		(4.30b)
	$\displaystyle u(t,0)=u(t,1)=0,\leavevmode\nobreak\ t\in[0,1],$		(4.30c)

onde o coeficiente de difusão $\lambda>0$ é um parâmetro a determinar. Sabendo que o problema tem solução analítica

u(t,x)=e^{-t}\operatorname{sen}(\pi x),

(4.31)

escolha um conjunto de amostras $\mathcal{D}=\left\{\left(\left(t^{(s)},x^{(s)}\right),u^{(s)}\right)\right\}_{% s=1}^{n_{s}}$ tal que seja possível estimar $\lambda$ com uma PINN

\tilde{u}=\mathcal{N}(t,x;\lambda).

(4.32)

Resposta.

$\lambda=1$

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Pedro H A Konzen

| | | |

		$\displaystyle{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1% }\pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\varepsilon_{% \lambda}:=\underbrace{\frac{1}{n_{\text{in}}}\sum_{s=1}^{n_{\text{in}}}\left\|% \mathcal{R}_{\lambda}\left(\boldsymbol{x}_{\text{in}}^{(s)}\right)\right\|^{2}}% _{\text{pts. internos}}}$		(4.17)
		$\displaystyle{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1% }\pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\quad+% \underbrace{\frac{1}{n_{\text{cc}}}\sum_{s=1}^{n_{\text{cc}}}\left\|\tilde{u}_{% \text{cc}}-u_{\text{cc}}\right\|^{2}}_{\text{c.i. \& c.c.}}}$
		$\displaystyle{\color[rgb]{1,0,0}\definecolor[named]{pgfstrokecolor}{rgb}{1,0,0% }\pgfsys@color@rgb@stroke{1}{0}{0}\pgfsys@color@rgb@fill{1}{0}{0}\quad+% \underbrace{\frac{p}{n_{s}}\sum_{s=1}^{n_{s}}\left\|\tilde{u}^{(s)}-u^{(s)}% \right\|^{2}}_{\text{amostras}}},$

		$\displaystyle{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1% }\pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\varepsilon_{% \lambda}:=\underbrace{\frac{1}{n_{\text{in}}}\sum_{s=1}^{n_{\text{in}}}\left\|% \mathcal{R}_{\lambda}\left(\boldsymbol{x}_{\text{in}}^{(s)}\right)\right\|^{2}}% _{\text{pts. internos}}}$		(4.17)
		$\displaystyle{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1% }\pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\quad+% \underbrace{\frac{1}{n_{\text{cc}}}\sum_{s=1}^{n_{\text{cc}}}\left\|\tilde{u}_{% \text{cc}}-u_{\text{cc}}\right\|^{2}}_{\text{c.i. \& c.c.}}}$
		$\displaystyle{\color[rgb]{1,0,0}\definecolor[named]{pgfstrokecolor}{rgb}{1,0,0% }\pgfsys@color@rgb@stroke{1}{0}{0}\pgfsys@color@rgb@fill{1}{0}{0}\quad+% \underbrace{\frac{p}{n_{s}}\sum_{s=1}^{n_{s}}\left\|\tilde{u}^{(s)}-u^{(s)}% \right\|^{2}}_{\text{amostras}}},$