Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Redes Neurais Artificiais
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
2.1 Unidade de Processamento
A unidade básica de processamento (neurônio artificial) do tipo perceptron segue o esquema dado na Fig. 2.1. Consiste na composição de uma função de ativação com a pré-ativação
| (2.1) | ||||
| (2.2) |
onde, é o vetor de entrada, é o vetor de pesos e é o bias. Escolhida uma função de ativação, a saída do neurônio é dada por
| (2.3) | ||||
| (2.4) |
O treinamento (calibração) consiste em determinar os parâmetros de forma que o neurônio forneça as saídas esperadas com base em um critério predeterminado.
Uma das vantagens deste modelo de neurônio é sua generalidade, i.e. pode ser aplicado a diferentes problemas. Na sequência, vamos aplicá-lo na resolução de um problema de classificação e noutro de regressão.
2.1.1 Um problema de classificação
Vamos desenvolver um perceptron que emule a operação (e-lógico). I.e, receba como entrada dois valores lógicos e (V, verdadeiro ou F, falso) e forneça como saída o valor lógico . Segue a tabela verdade do :
| R | ||
|---|---|---|
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | F |
Modelo
Nosso modelo de neurônio será um perceptron com duas entradas e a função sinal
| (2.5) |
como função de ativação, i.e.
| (2.6) | ||||
| (2.7) |
onde e são parâmetros a determinar.
Pré-processamento
Uma vez que nosso modelo recebe valores e retorna , precisamos (pre)processar os dados do problema de forma a utilizá-los. Uma forma, é assumir que todo valor negativo está associado ao valor lógico (falso) e positivo ao valor lógico (verdadeiro). Desta forma, os dados podem ser interpretados como na tabela abaixo.
| 1 | 1 | 1 |
|---|---|---|
| 1 | -1 | -1 |
| -1 | 1 | -1 |
| -1 | -1 | -1 |
Treinamento
Agora, nos falta treinar nosso neurônio para fornecer o valor de esperado para cada dada entrada . Isso consiste em um método para escolhermos os parâmetros que sejam adequados para esta tarefa. Vamos explorar mais sobre isso na sequência do texto e, aqui, apenas escolhemos
| (2.8) | |||
| (2.9) |
Com isso, nosso perceptron é
| (2.10) |
Verifique que ele satisfaz a tabela verdade acima!
Implementação
Interpretação geométrica
Empregamos o seguinte modelo de neurônio
| (2.11) |
Observamos que
| (2.12) |
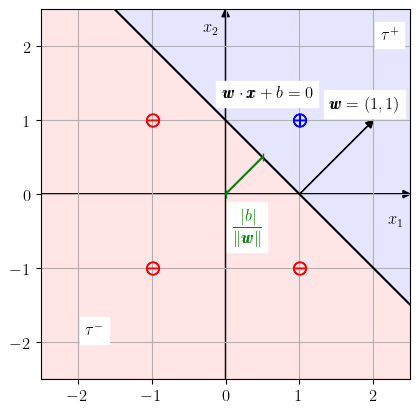
corresponde à equação geral de uma reta no plano . Esta reta divide o plano em dois semiplanos
| (2.13) | |||
| (2.14) |
O primeiro está na direção do vetor normal à reta e o segundo no sentido oposto. Com isso, o problema de treinar nosso neurônio para o problema de classificação consiste em encontrar a reta
| (2.15) |
de forma que o ponto esteja no semiplano positivo e os demais pontos no semiplano negativo . Consultamos a Figura 2.2.
Algoritmo de treinamento: perceptron
O algoritmo de treinamento perceptron permite calibrar os pesos de um neurônio para fazer a classificação de dados linearmente separáveis. Trata-se de um algoritmo para o treinamento supervisionado de um neurônio, i.e. a calibração dos pesos é feita com base em um dado conjunto de amostras de treinamento.
Seja dado um conjunto de treinamento , onde é o número de amostras. O algoritmo consiste no seguinte:
-
1.
, .
-
2.
Para :
-
(a)
Para :
-
i.
Se :
-
A.
-
B.
-
A.
-
i.
-
(a)
onde, é um dado número de épocas22endnote: 2Número de vezes que as amostrar serão percorridas para realizar a correção dos pesos..
2.1.2 Problema de regressão
Vamos treinar um perceptron para resolver o problema de regressão linear para os seguintes dados
| s | ||
|---|---|---|
| 1 | 0.5 | 1.2 |
| 2 | 1.0 | 2.1 |
| 3 | 1.5 | 2.6 |
| 4 | 2.0 | 3.6 |
Modelo
Vamos determinar o perceptron33endnote: 3Escolhendo como função de ativação.
| (2.16) |
que melhor se ajusta a este conjunto de dados , .
Treinamento
A ideia é que o perceptron seja tal que minimize o erro quadrático médio (MSE, do inglês, Mean Squared Error), i.e.
| (2.17) |
Vamos denotar a função erro (em inglês, loss function) por
| (2.18) | ||||
| (2.19) |
Observamos que o problema (2.17) é equivalente a um problema linear de mínimos quadrados. A solução é obtida resolvendo-se a equação normal44endnote: 4Consulte o Exercício 2.1.4.
| (2.20) |
onde é o vetor dos parâmetros a determinar e é a matriz dada por
| (2.21) |
Implementação
Resultado
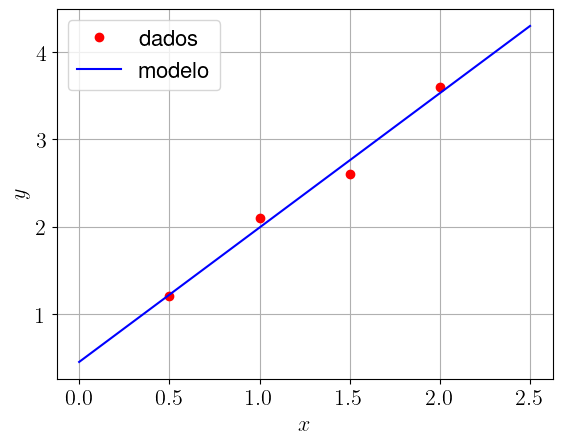
Nosso perceptron corresponde ao modelo
| (2.22) |
com pesos treinados e . Ele corresponde à reta que melhor se ajusta ao conjunto de dados de dado na tabela acima. Consultamos a Figura 2.3.
2.1.3 Exercícios
E. 2.1.1.
Crie um perceptron que emule a operação lógica do (ou-lógico).
| V | V | V |
| V | F | V |
| F | V | V |
| F | F | F |
E. 2.1.2.
Busque criar um perceptron que emule a operação lógica do xor.
| V | V | F |
| V | F | V |
| F | V | V |
| F | F | F |
É possível? Justifique sua resposta.
Resposta 0.
Dica: verifique que sua matriz hessiana é positiva definida.
Resposta 0.
Dica: consulte a ligação Notas de Aula: Matemática Numérica: 7.1 Problemas lineares.
E. 2.1.5.
Crie um perceptron com função de ativação que melhor se ajuste ao seguinte conjunto de dados:
| s | ||
|---|---|---|
| 1 | -1,0 | -0,8 |
| 2 | -0,7 | -0,7 |
| 3 | -0,3 | -0,5 |
| 4 | 0,0 | -0,4 |
| 5 | 0,2 | -0,2 |
| 6 | 0,5 | 0,0 |
| 7 | 1,0 | 0,3 |
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.
Redes Neurais Artificiais
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
2.1 Unidade de Processamento
A unidade básica de processamento (neurônio artificial) do tipo perceptron segue o esquema dado na Fig. 2.1. Consiste na composição de uma função de ativação com a pré-ativação
| (2.1) | ||||
| (2.2) |
onde, é o vetor de entrada, é o vetor de pesos e é o bias. Escolhida uma função de ativação, a saída do neurônio é dada por
| (2.3) | ||||
| (2.4) |
O treinamento (calibração) consiste em determinar os parâmetros de forma que o neurônio forneça as saídas esperadas com base em um critério predeterminado.
Uma das vantagens deste modelo de neurônio é sua generalidade, i.e. pode ser aplicado a diferentes problemas. Na sequência, vamos aplicá-lo na resolução de um problema de classificação e noutro de regressão.
2.1.1 Um problema de classificação
Vamos desenvolver um perceptron que emule a operação (e-lógico). I.e, receba como entrada dois valores lógicos e (V, verdadeiro ou F, falso) e forneça como saída o valor lógico . Segue a tabela verdade do :
| R | ||
|---|---|---|
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | F |
Modelo
Nosso modelo de neurônio será um perceptron com duas entradas e a função sinal
| (2.5) |
como função de ativação, i.e.
| (2.6) | ||||
| (2.7) |
onde e são parâmetros a determinar.
Pré-processamento
Uma vez que nosso modelo recebe valores e retorna , precisamos (pre)processar os dados do problema de forma a utilizá-los. Uma forma, é assumir que todo valor negativo está associado ao valor lógico (falso) e positivo ao valor lógico (verdadeiro). Desta forma, os dados podem ser interpretados como na tabela abaixo.
| 1 | 1 | 1 |
|---|---|---|
| 1 | -1 | -1 |
| -1 | 1 | -1 |
| -1 | -1 | -1 |
Treinamento
Agora, nos falta treinar nosso neurônio para fornecer o valor de esperado para cada dada entrada . Isso consiste em um método para escolhermos os parâmetros que sejam adequados para esta tarefa. Vamos explorar mais sobre isso na sequência do texto e, aqui, apenas escolhemos
| (2.8) | |||
| (2.9) |
Com isso, nosso perceptron é
| (2.10) |
Verifique que ele satisfaz a tabela verdade acima!
Implementação
Interpretação geométrica
Empregamos o seguinte modelo de neurônio
| (2.11) |
Observamos que
| (2.12) |
corresponde à equação geral de uma reta no plano . Esta reta divide o plano em dois semiplanos
| (2.13) | |||
| (2.14) |
O primeiro está na direção do vetor normal à reta e o segundo no sentido oposto. Com isso, o problema de treinar nosso neurônio para o problema de classificação consiste em encontrar a reta
| (2.15) |
de forma que o ponto esteja no semiplano positivo e os demais pontos no semiplano negativo . Consultamos a Figura 2.2.

Algoritmo de treinamento: perceptron
O algoritmo de treinamento perceptron permite calibrar os pesos de um neurônio para fazer a classificação de dados linearmente separáveis. Trata-se de um algoritmo para o treinamento supervisionado de um neurônio, i.e. a calibração dos pesos é feita com base em um dado conjunto de amostras de treinamento.
Seja dado um conjunto de treinamento , onde é o número de amostras. O algoritmo consiste no seguinte:
-
1.
, .
-
2.
Para :
-
(a)
Para :
-
i.
Se :
-
A.
-
B.
-
A.
-
i.
-
(a)
onde, é um dado número de épocas22endnote: 2Número de vezes que as amostrar serão percorridas para realizar a correção dos pesos..
2.1.2 Problema de regressão
Vamos treinar um perceptron para resolver o problema de regressão linear para os seguintes dados
| s | ||
|---|---|---|
| 1 | 0.5 | 1.2 |
| 2 | 1.0 | 2.1 |
| 3 | 1.5 | 2.6 |
| 4 | 2.0 | 3.6 |
Modelo
Vamos determinar o perceptron33endnote: 3Escolhendo como função de ativação.
| (2.16) |
que melhor se ajusta a este conjunto de dados , .
Treinamento
A ideia é que o perceptron seja tal que minimize o erro quadrático médio (MSE, do inglês, Mean Squared Error), i.e.
| (2.17) |
Vamos denotar a função erro (em inglês, loss function) por
| (2.18) | ||||
| (2.19) |
Observamos que o problema (2.17) é equivalente a um problema linear de mínimos quadrados. A solução é obtida resolvendo-se a equação normal44endnote: 4Consulte o Exercício 2.1.4.
| (2.20) |
onde é o vetor dos parâmetros a determinar e é a matriz dada por
| (2.21) |
Implementação
Resultado
Nosso perceptron corresponde ao modelo
| (2.22) |
com pesos treinados e . Ele corresponde à reta que melhor se ajusta ao conjunto de dados de dado na tabela acima. Consultamos a Figura 2.3.

2.1.3 Exercícios
E. 2.1.1.
Crie um perceptron que emule a operação lógica do (ou-lógico).
| V | V | V |
| V | F | V |
| F | V | V |
| F | F | F |
E. 2.1.2.
Busque criar um perceptron que emule a operação lógica do xor.
| V | V | F |
| V | F | V |
| F | V | V |
| F | F | F |
É possível? Justifique sua resposta.
Resposta 0.
Dica: verifique que sua matriz hessiana é positiva definida.
Resposta 0.
Dica: consulte a ligação Notas de Aula: Matemática Numérica: 7.1 Problemas lineares.
E. 2.1.5.
Crie um perceptron com função de ativação que melhor se ajuste ao seguinte conjunto de dados:
| s | ||
|---|---|---|
| 1 | -1,0 | -0,8 |
| 2 | -0,7 | -0,7 |
| 3 | -0,3 | -0,5 |
| 4 | 0,0 | -0,4 |
| 5 | 0,2 | -0,2 |
| 6 | 0,5 | 0,0 |
| 7 | 1,0 | 0,3 |
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.