Política de uso de dados

Ao navegar por este site, você concorda com a política de uso de dados.

Política de uso de dados

Ao navegar por este site, você concorda com a política de uso de dados.

| | | |

Redes Neurais Artificiais

4 Redes Informadas pela Física 4 Redes Informadas pela Física 4.2 Aplicação: Equação do Calor

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

4.1 Aplicação: Equação de Poisson

Vamos criar uma MLP para resolver o problema de Poisson¹²¹²endnote: ¹²Siméon Denis Poisson, 1781 - 1840, matemático francês. Fonte: Wikipédia:Siméon Denis Poisson.


	$\displaystyle\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% -\Delta u=f,\leavevmode\nobreak\ \boldsymbol{x}\in\mathcal{D}=(-1,1)^{2},$		(4.1a)
	$\displaystyle\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% u=0,\leavevmode\nobreak\ \boldsymbol{x}\in\partial D,$		(4.1b)

com fonte dada

f(x_{1},x_{2})=\pi^{2}\operatorname{sen}(\pi x_{1})\operatorname{sen}(\pi x_{2% }).

(4.2)

No treinamento, vamos usar a função erro baseada no resíduo da equação de Poisson (4.1a) e nas condições de contorno (4.1b). Mais especificamente, assumimos a função erro

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\varepsilon:=% \underbrace{\frac{1}{n_{s,in}}\sum_{s=1}^{n_{s,in}}\left|\mathcal{R}\left(% \tilde{u}^{(s)}\right)\right|^{2}}_{\text{resíduo}}+\underbrace{\frac{1}{n_{s,% cc}}\sum_{s=1}^{n_{s,cc}}\left|\tilde{u}^{s}\right|^{2}}_{\text{c.c.}},

(4.3)

onde o resíduo é definido por

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\mathcal{R}% \left(\tilde{u}^{(s)}\right):=f+\Delta\tilde{u}^{(s)}.

(4.4)

A cada época, conjuntos de pontos $\left\{\boldsymbol{x}^{(s)}\right\}_{s=1}^{n_{s,in}}\subset\mathcal{D}$ e $\left\{\boldsymbol{x}^{(s)}\right\}_{s=1}^{n_{s,cc}}\subset\partial\mathcal{D}$ são randomicamente gerados com distribuição uniforme.

Observação 4.1.1.

O problema de Poisson (4.1) tem solução analítica

u(x_{1},x_{2})=\operatorname{sen}(\pi x_{1})\operatorname{sen}(\pi x_{2}).

(4.5)

É importante observar que o treinamento da MLP não depende de conhecermos a solução. Aqui, vamos usá-la apenas para compararmos a solução MLP com a analítica.

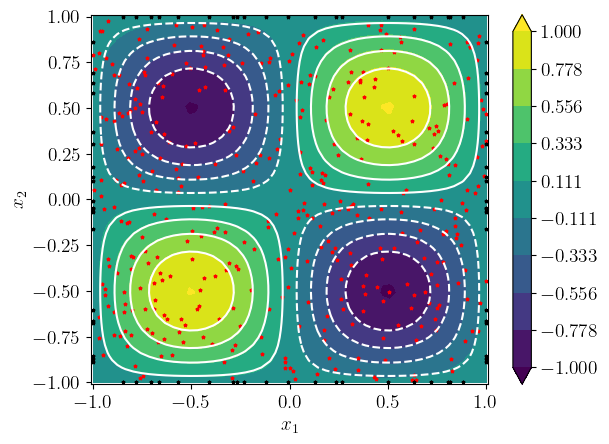
Refer to caption — Figura 4.1: Aproximação MLP da função solução do problema de Poisson (4.1). Linhas: isolinhas da solução analítica. Mapa de cores: solução MLP. Estrelas: pontos de treinamentos na última época.

Código 13: py_pinn_poisson

⬇

1 import torch

2 from torch import pi, sin

4 # modelo

5 nn = 50

6 model = torch.nn.Sequential()

7 model.add_module('layer_1', torch.nn.Linear(2,nn))

8 model.add_module('fun_1', torch.nn.Tanh())

9 model.add_module('layer_2', torch.nn.Linear(nn,nn))

10 model.add_module('fun_2', torch.nn.Tanh())

11 model.add_module('layer_3', torch.nn.Linear(nn,nn))

12 model.add_module('fun_3', torch.nn.Tanh())

13 model.add_module('layer_4', torch.nn.Linear(nn,1))

15 # otimizador

16 optim = torch.optim.SGD(model.parameters(),

17 lr = 1e-3, momentum=0.9)

19 # fonte

20 def f(x1, x2):

21 return 2.*pi**2*sin(pi*x1)*sin(pi*x2)

23 # treinamento

24 ns_in = 400

25 ns_cc = 20

26 nepochs = 50000

27 tol = 1e-3

29 ## pontos de validação

30 ns_val = 50

31 x1_val = torch.linspace(-1., 1., steps=ns_val)

32 x2_val = torch.linspace(-1., 1., steps=ns_val)

33 X1_val, X2_val = torch.meshgrid(x1_val, x2_val, indexing='ij')

34 X_val = torch.hstack((X1_val.reshape(ns_val**2,1),

35 X2_val.reshape(ns_val**2,1)))

37 for epoch in range(nepochs):

39 # forward

40 X1 = 2.*torch.rand(ns_in, 1) - 1.

41 X2 = 2.*torch.rand(ns_in, 1) - 1.

42 X = torch.hstack((X1, X2))

43 X.requires_grad = True

45 U = model(X)

47 # gradientes

48 D1U = torch.autograd.grad(

49 U, X,

50 grad_outputs=torch.ones_like(U),

51 retain_graph=True,

52 create_graph=True)[0]

53 D2UX1 = torch.autograd.grad(

54 D1U[:,0:1], X,

55 grad_outputs=torch.ones_like(D1U[:,0:1]),

56 retain_graph=True,

57 create_graph=True)[0]

58 D2UX2 = torch.autograd.grad(

59 D1U[:,1:2], X,

60 grad_outputs=torch.ones_like(D1U[:,1:2]),

61 retain_graph=True,

62 create_graph=True)[0]

64 # fonte

65 F = f(X1, X2)

67 # loss pts internos

68 lin = torch.mean((F + D2UX1[:,0:1] + D2UX2[:,1:2])**2)

70 # contornos

71 ## c.c. 1

72 X1 = 2.*torch.rand(ns_cc, 1) - 1.

73 Xcc1 = torch.hstack((X1, -torch.ones((ns_cc,1))))

74 Ucc1 = model(Xcc1)

76 ## c.c. 3

77 Xcc3 = torch.hstack((X1, torch.ones((ns_cc,1))))

78 Ucc3 = model(Xcc3)

80 ## c.c. 4

81 X2 = 2.*torch.rand(ns_cc, 1) - 1.

82 Xcc4 = torch.hstack((-torch.ones((ns_cc,1)), X2))

83 Ucc4 = model(Xcc4)

85 ## c.c. 2

86 Xcc2 = torch.hstack((torch.ones((ns_cc,1)), X2))

87 Ucc2 = model(Xcc2)

89 # loss cc

90 lcc = 1./(4.*ns_cc) * torch.sum(Ucc1**2 + Ucc2**2 + Ucc3**2 + Ucc4**2)

92 # loss

93 loss = lin + lcc

95 if ((epoch % 500 == 0) or (loss.item() < tol)):

96 print(f'{epoch}: loss = {loss.item():.4e}')

98 if (loss.item() < tol):

99 break

100

101 optim.zero_grad()

102 loss.backward()

103 optim.step()

4.1.1 Exercícios

E. 4.1.1.

Crie uma MLP para resolver

	$\displaystyle-\Delta u=0,\leavevmode\nobreak\ \boldsymbol{x}\in D=(0,1)^{2},$		(4.6)
	$\displaystyle u(x_{1},0)=x1(1-x_{1}),0\leq x_{1}\leq 1,$		(4.7)
	$\displaystyle u(1,x_{2})=x2(1-x_{2}),0<x_{2}\leq 1,$		(4.8)
	$\displaystyle u(x_{1},1)=x1(1-x_{1}),0\leq x_{1}<1,$		(4.9)
	$\displaystyle u(0,x_{2})=x2(1-x_{2}),0<x_{2}<1.$		(4.10)

Resposta 0.

Dica: solução analítica $u(x_{1},x_{2})=x_{1}(1-x_{1})-x_{2}(1-x_{2})$ .

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.