Política de uso de dados

Ao navegar por este site, você concorda com a política de uso de dados.

Política de uso de dados

Ao navegar por este site, você concorda com a política de uso de dados.

| | | |

Redes Neurais Artificiais

3 Perceptron Multicamadas 3.1 Modelo MLP 3.3 Aplicação: Aproximação de Funções

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

3.2 Aplicação: Problema de Classificação Binária

Em construção

Vamos estudar uma aplicação de redes neurais artificiais em um problema de classificação binária não linear.

3.2.1 Dados

Em construção

Vamos desenvolver uma rede do tipo Perceptron Multicamadas (MLP) para a classificação binária de pontos, com base nos seguintes dados.

⬇

1from sklearn.datasets import make_circles

2import matplotlib.pyplot as plt

4plt.rcParams.update({

5 "text.usetex": True,

6 "font.family": "serif",

7 "font.size": 14

8 })

10# data

11print('data')

12n_samples = 1000

13print(f'n_samples = {n_samples}')

14# X = points, y = labels

15X, y = make_circles(n_samples,

16 noise=0.03, # add noise

17 random_state=42) # random seed

19fig = plt.figure()

20ax = fig.add_subplot()

21ax.scatter(X[:,0], X[:,1], c=y, cmap=plt.cm.coolwarm)

22ax.grid()

23ax.set_xlabel('$x_1$')

24ax.set_ylabel('$x_2$')

25plt.show()

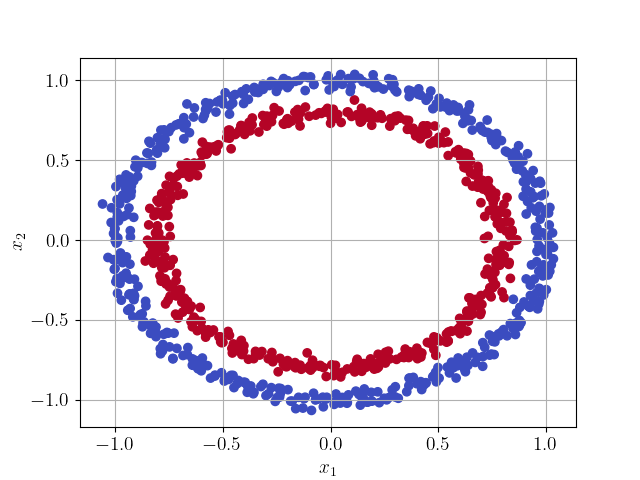
Refer to caption — Figura 3.2: Dados para a o problema de classificação binária não linear.

3.2.2 Modelo

Em construção

Vamos usar uma MLP de estrutura 2-10-1, com função de ativação

\operatorname{elu}(x)=\left\{\begin{array}[]{ll}x&,x>0\\ \alpha\left(e^{x}-1\right)&,x\leq 0\end{array}\right.

(3.12)

na camada escondida e

\operatorname{sigmoid}(x)=\frac{1}{1+e^{x}}

(3.13)

na saída da rede.

Para o treinamento e teste, vamos randomicamente separar os dados em um conjunto de treinamento $\{\boldsymbol{x}_{\text{train}}^{(k)},y_{\text{train}}^{(k)}\}_{k=1}^{n_{\text% {train}}}$ e um conjunto de teste $\{\boldsymbol{x}_{\text{test}}^{(k)},y_{\text{test}}^{(k)}\}_{k=1}^{n_{\text{% test}}}$ , com $y=0$ para os pontos azuis e $y=1$ para os pontos vermelhos.

3.2.3 Treinamento e Teste

Em construção

Código 7: mlp_classbin.py

⬇

1import torch

2from sklearn.datasets import make_circles

3from sklearn.model_selection import train_test_split

4import matplotlib.pyplot as plt

6# data

7print('data')

8n_samples = 1000

9print(f'n_samples = {n_samples}')

10# X = points, y = labels

11X, y = make_circles(n_samples,

12 noise=0.03, # add noise

13 random_state=42) # random seed

15## numpy -> torch

16X = torch.from_numpy(X).type(torch.float)

17y = torch.from_numpy(y).type(torch.float).reshape(-1,1)

19## split into train and test datasets

20print('Data: train and test sets')

21X_train, X_test, y_train, y_test = train_test_split(X,

22 y,

23 test_size=0.2,

24 random_state=42)

25print(f'n_train = {len(X_train)}')

26print(f'n_test = {len(X_test)}')

27plt.close()

28plt.scatter(X_train[:,0], X_train[:,1], c=y_train,

29 marker='o', cmap=plt.cm.coolwarm, alpha=0.3)

30plt.scatter(X_test[:,0], X_test[:,1], c=y_test,

31 marker='*', cmap=plt.cm.coolwarm)

32plt.show()

34# model

35model = torch.nn.Sequential(

36 torch.nn.Linear(2, 10),

37 torch.nn.ELU(),

38 torch.nn.Linear(10, 1),

39 torch.nn.Sigmoid()

40 )

42# loss fun

43loss_fun = torch.nn.BCELoss()

45# optimizer

46optimizer = torch.optim.SGD(model.parameters(),

47 lr = 1e-1)

49# evaluation metric

50def accuracy_fun(y_pred, y_exp):

51 correct = torch.eq(y_pred, y_exp).sum().item()

52 acc = correct/len(y_exp) * 100

53 return acc

55# train

56n_epochs = 10000

57n_out = 100

59for epoch in range(n_epochs):

60 model.train()

62 y_pred = model(X_train)

64 loss = loss_fun(y_pred, y_train)

66 acc = accuracy_fun(torch.round(y_pred),

67 y_train)

69 optimizer.zero_grad()

70 loss.backward()

71 optimizer.step()

73 model.eval()

75 #testing

76 if ((epoch+1) % n_out == 0):

77 with torch.inference_mode():

78 y_pred_test = model(X_test)

79 loss_test = loss_fun(y_pred_test,

80 y_test)

81 acc_test = accuracy_fun(torch.round(y_pred_test),

82 y_test)

84 print(f'{epoch+1}: loss = {loss:.5e}, accuracy = {acc:.2f}%')

85 print(f'\ttest: loss = {loss:.5e}, accuracy = {acc:.2f}%\n')

3.2.4 Verificação

Em construção

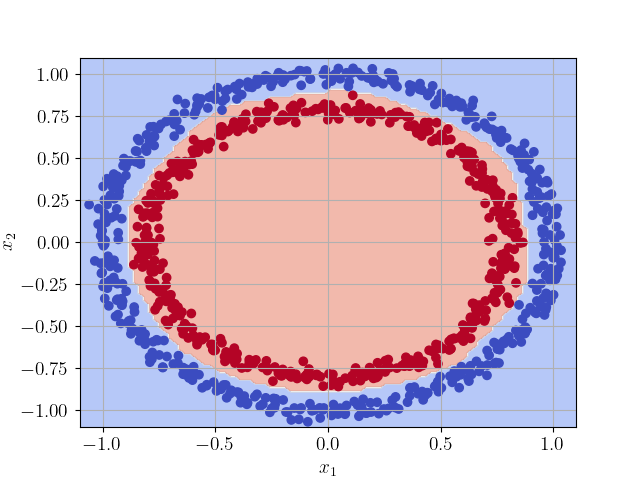
Para a verificação, testamos o modelo em uma malha uniforme de $100\times 100$ pontos no domínio $[-1,1]^{2}$ . Consulte a Figure 3.3.

⬇

1# malha de pontos

2xx = torch.linspace(-1.1, 1.1, 100)

3Xg, Yg = torch.meshgrid(xx, xx)

5# valores estimados

6Zg = torch.empty_like(Xg)

7for i,xg in enumerate(xx):

8 for j,yg in enumerate(xx):

9 z = model(torch.tensor([[xg, yg]])).detach()

10 Zg[i, j] = torch.round(z)

12# visualização

13fig = plt.figure()

14ax = fig.add_subplot()

15ax.contourf(Xg, Yg, Zg, levels=2, cmap=plt.cm.coolwarm, alpha=0.5)

16ax.scatter(X[:,0], X[:,1], c=y, cmap=plt.cm.coolwarm)

17plt.show()

3.2.5 Exercícios

Em construção

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Redes Neurais Artificiais

3 Perceptron Multicamadas 3.1 Modelo MLP 3.3 Aplicação: Aproximação de Funções

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

3.2 Aplicação: Problema de Classificação Binária

Em construção

Vamos estudar uma aplicação de redes neurais artificiais em um problema de classificação binária não linear.

3.2.1 Dados

Em construção

Vamos desenvolver uma rede do tipo Perceptron Multicamadas (MLP) para a classificação binária de pontos, com base nos seguintes dados.

⬇

1from sklearn.datasets import make_circles

2import matplotlib.pyplot as plt

4plt.rcParams.update({

5 "text.usetex": True,

6 "font.family": "serif",

7 "font.size": 14

8 })

10# data

11print('data')

12n_samples = 1000

13print(f'n_samples = {n_samples}')

14# X = points, y = labels

15X, y = make_circles(n_samples,

16 noise=0.03, # add noise

17 random_state=42) # random seed

19fig = plt.figure()

20ax = fig.add_subplot()

21ax.scatter(X[:,0], X[:,1], c=y, cmap=plt.cm.coolwarm)

22ax.grid()

23ax.set_xlabel('$x_1$')

24ax.set_ylabel('$x_2$')

25plt.show()

3.2.2 Modelo

Em construção

Vamos usar uma MLP de estrutura 2-10-1, com função de ativação

\operatorname{elu}(x)=\left\{\begin{array}[]{ll}x&,x>0\\ \alpha\left(e^{x}-1\right)&,x\leq 0\end{array}\right.

(3.12)

na camada escondida e

\operatorname{sigmoid}(x)=\frac{1}{1+e^{x}}

(3.13)

na saída da rede.

3.2.3 Treinamento e Teste

Em construção

Código 7: mlp_classbin.py

⬇

1import torch

2from sklearn.datasets import make_circles

3from sklearn.model_selection import train_test_split

4import matplotlib.pyplot as plt

6# data

7print('data')

8n_samples = 1000

9print(f'n_samples = {n_samples}')

10# X = points, y = labels

11X, y = make_circles(n_samples,

12 noise=0.03, # add noise

13 random_state=42) # random seed

15## numpy -> torch

16X = torch.from_numpy(X).type(torch.float)

17y = torch.from_numpy(y).type(torch.float).reshape(-1,1)

19## split into train and test datasets

20print('Data: train and test sets')

21X_train, X_test, y_train, y_test = train_test_split(X,

22 y,

23 test_size=0.2,

24 random_state=42)

25print(f'n_train = {len(X_train)}')

26print(f'n_test = {len(X_test)}')

27plt.close()

28plt.scatter(X_train[:,0], X_train[:,1], c=y_train,

29 marker='o', cmap=plt.cm.coolwarm, alpha=0.3)

30plt.scatter(X_test[:,0], X_test[:,1], c=y_test,

31 marker='*', cmap=plt.cm.coolwarm)

32plt.show()

34# model

35model = torch.nn.Sequential(

36 torch.nn.Linear(2, 10),

37 torch.nn.ELU(),

38 torch.nn.Linear(10, 1),

39 torch.nn.Sigmoid()

40 )

42# loss fun

43loss_fun = torch.nn.BCELoss()

45# optimizer

46optimizer = torch.optim.SGD(model.parameters(),

47 lr = 1e-1)

49# evaluation metric

50def accuracy_fun(y_pred, y_exp):

51 correct = torch.eq(y_pred, y_exp).sum().item()

52 acc = correct/len(y_exp) * 100

53 return acc

55# train

56n_epochs = 10000

57n_out = 100

59for epoch in range(n_epochs):

60 model.train()

62 y_pred = model(X_train)

64 loss = loss_fun(y_pred, y_train)

66 acc = accuracy_fun(torch.round(y_pred),

67 y_train)

69 optimizer.zero_grad()

70 loss.backward()

71 optimizer.step()

73 model.eval()

75 #testing

76 if ((epoch+1) % n_out == 0):

77 with torch.inference_mode():

78 y_pred_test = model(X_test)

79 loss_test = loss_fun(y_pred_test,

80 y_test)

81 acc_test = accuracy_fun(torch.round(y_pred_test),

82 y_test)

84 print(f'{epoch+1}: loss = {loss:.5e}, accuracy = {acc:.2f}%')

85 print(f'\ttest: loss = {loss:.5e}, accuracy = {acc:.2f}%\n')

3.2.4 Verificação

Em construção

Para a verificação, testamos o modelo em uma malha uniforme de $100\times 100$ pontos no domínio $[-1,1]^{2}$ . Consulte a Figure 3.3.

⬇

1# malha de pontos

2xx = torch.linspace(-1.1, 1.1, 100)

3Xg, Yg = torch.meshgrid(xx, xx)

5# valores estimados

6Zg = torch.empty_like(Xg)

7for i,xg in enumerate(xx):

8 for j,yg in enumerate(xx):

9 z = model(torch.tensor([[xg, yg]])).detach()

10 Zg[i, j] = torch.round(z)

12# visualização

13fig = plt.figure()

14ax = fig.add_subplot()

15ax.contourf(Xg, Yg, Zg, levels=2, cmap=plt.cm.coolwarm, alpha=0.5)

16ax.scatter(X[:,0], X[:,1], c=y, cmap=plt.cm.coolwarm)

17plt.show()

3.2.5 Exercícios

Em construção

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Pedro H A Konzen

| | | |