Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Redes Neurais Artificiais
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
3.4 Diferenciação Automática
Diferenciação automática é um conjunto de técnicas para a computação de derivadas numéricas em um programa de computador. Explora-se o fato de que um programa computacional executa uma sequência de operações aritméticas e funções elementares, podendo-se computar a derivada por aplicações da regra da cadeia.
PyTorch computa o gradiente (derivada) de uma função a partir de seu grafo computacional. Os gradientes são computados por retropropagação. Por exemplo, para a computação do gradiente
| (3.19) |
primeiramente, propaga-se a entrada pela função computacional , obtendo-se . Então, o gradiente é computado por retropropagação.
Exemplo 3.4.1.
Consideramos a função e vamos computar
| (3.20) |
por diferenciação automática.
Antes, observamos que, pela regra da cadeia, denotamos e calculamos
| (3.21) | ||||
| (3.22) | ||||
| (3.23) |
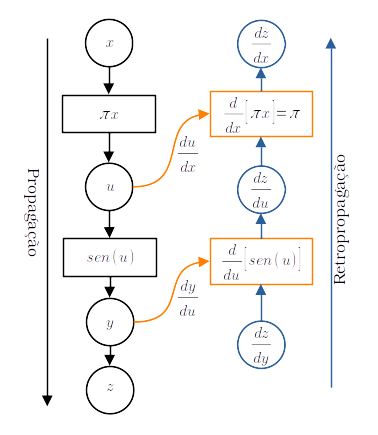
Agora, observamos que a computação de pode ser representada pelo grafo de propagação mostrado na Figura 3.6. Para a computação do gradiente, adicionamos uma variável fictícia . Na retropropagação, computamos
| (3.24a) | |||
| (3.24b) | |||
| (3.24c) | |||
| (3.24d) | |||
| (3.24e) | |||
A computação do gradiente também acaba por construir um novo grafo (consulte Figura 3.6). Este, por sua vez, pode ser usado para a computação da diferenciação automática de segunda ordem, i.e. para a derivação de segunda ordem.
Exemplo 3.4.2.
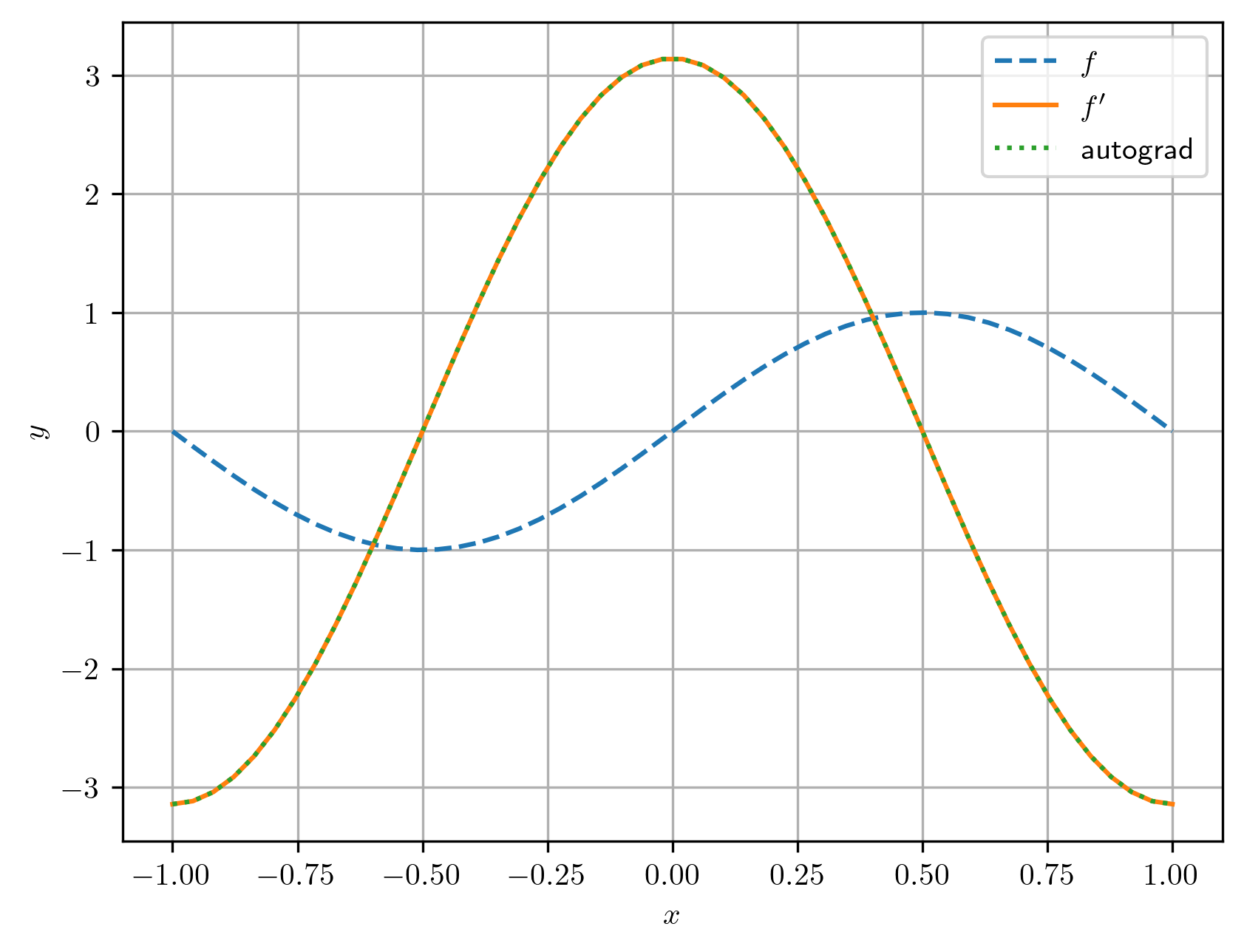
Consideramos a função . No exemplo anterior, computamos por diferenciação automática. No Código 10, os gradientes foram computados com o comando
Alternativamente, podemos usar
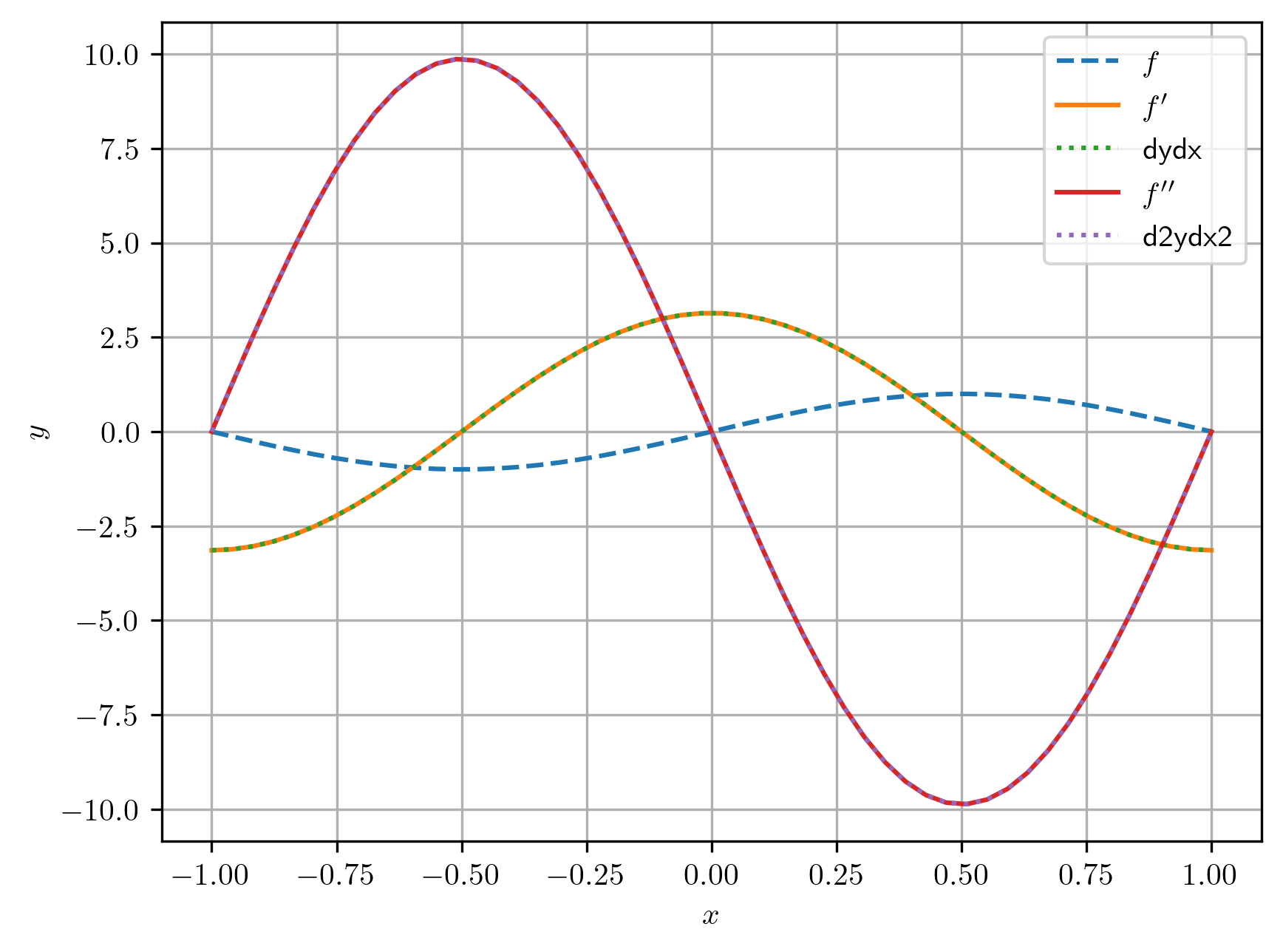
Este comando computa , mas avisa o PyTorch que os grafos computacionais sejam mantidos e que um novo grafo seja gerado da retropropagação. Com isso, podemos computar o gradiente do gradiente, como no código abaixo.
3.4.1 Autograd MLP
Os conceitos de diferenciação automática (autograd) são diretamente estendidos para redes do tipo Perceptron Multicamadas (MLP, do inglês, Multilayer Perceptron). Uma MLP é uma composição de funções definidas por parâmetros (pesos e biases). Seu treinamento ocorre em duas etapas1010endnote: 10Para mais detalhes, consulte a Subseção 3.1.1.:
-
1.
Propagação (forward): os dados de entrada são propagados para todas as funções da rede, produzindo a saída estimada.
-
2.
Retropropagação (backward): a computação do gradiente do erro1111endnote: 11Medida da diferença entre o valor estimado e o valor esperado. em relação aos parâmetros da rede é realizado coletando as derivadas (gradientes) das funções da rede. Pela regra da cadeia, essa coleta é feita a partir da camada de saída em direção a camada de entrada da rede.
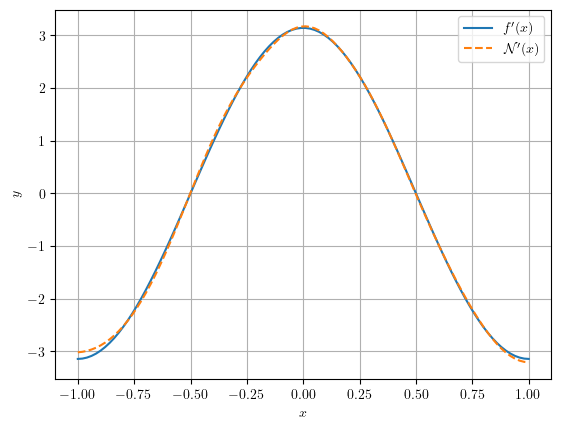
No seguinte exemplo, exploramos o fato de MLPs serem aproximadoras universais e avaliamos a derivada de uma MLP na aproximação de uma função.
Exemplo 3.4.3.
Vamos criar uma MLP
| (3.25) |
que aproxima a função
| (3.26) |
Em seguida, computamos, por diferenciação automática, o gradiente
| (3.27) |
e comparamos com o resultado esperado
| (3.28) |
3.4.2 Exercícios
E. 3.4.1.
Por diferenciação automática, compute o gradiente (a derivada) das seguintes funções
-
a)
para valores .
-
b)
para valores .
-
c)
para valores .
-
d)
para valores .
Em cada caso, compare os valores computados com os valores esperados.
E. 3.4.2.
Em cada item do Exercício 3.4.1, faça um fluxograma dos grafos computacionais da propagação e da retropropagação na computação dos gradientes.
E. 3.4.3.
Em cada item do Exercício 3.4.1, compute a derivada de segunda ordem da função indicada. Compare os valores computados com os valores esperados.
E. 3.4.4.
Por diferenciação automática, compute os gradientes das seguintes funções:
-
a)
para valores .
-
b)
para valores .
Em cada caso, compare os valores computados com os valores esperados.
E. 3.4.5.
Para as funções de cada item do Exercício 3.4.6, compute:
-
a)
.
-
b)
.
-
c)
.
Compare os valores computados com os valores esperados.
E. 3.4.6.
Em cada item do Exercício 3.4.6, compute o laplacino da função indicada. Compare os valores computados com os valores esperados.
E. 3.4.7.
Seja a função definida por
| (3.29) |
no domínio . Por diferenciação automática e para valores no domínio da função, compute:
-
a)
.
-
b)
.
-
c)
.
-
d)
.
-
e)
.
-
f)
.
-
g)
.
-
h)
.
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.
Redes Neurais Artificiais
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
3.4 Diferenciação Automática
Diferenciação automática é um conjunto de técnicas para a computação de derivadas numéricas em um programa de computador. Explora-se o fato de que um programa computacional executa uma sequência de operações aritméticas e funções elementares, podendo-se computar a derivada por aplicações da regra da cadeia.
PyTorch computa o gradiente (derivada) de uma função a partir de seu grafo computacional. Os gradientes são computados por retropropagação. Por exemplo, para a computação do gradiente
| (3.19) |
primeiramente, propaga-se a entrada pela função computacional , obtendo-se . Então, o gradiente é computado por retropropagação.
Exemplo 3.4.1.
Consideramos a função e vamos computar
| (3.20) |
por diferenciação automática.
Antes, observamos que, pela regra da cadeia, denotamos e calculamos
| (3.21) | ||||
| (3.22) | ||||
| (3.23) |

Agora, observamos que a computação de pode ser representada pelo grafo de propagação mostrado na Figura 3.6. Para a computação do gradiente, adicionamos uma variável fictícia . Na retropropagação, computamos
| (3.24a) | |||
| (3.24b) | |||
| (3.24c) | |||
| (3.24d) | |||
| (3.24e) | |||

A computação do gradiente também acaba por construir um novo grafo (consulte Figura 3.6). Este, por sua vez, pode ser usado para a computação da diferenciação automática de segunda ordem, i.e. para a derivação de segunda ordem.
Exemplo 3.4.2.
Consideramos a função . No exemplo anterior, computamos por diferenciação automática. No Código 10, os gradientes foram computados com o comando
Alternativamente, podemos usar
Este comando computa , mas avisa o PyTorch que os grafos computacionais sejam mantidos e que um novo grafo seja gerado da retropropagação. Com isso, podemos computar o gradiente do gradiente, como no código abaixo.

3.4.1 Autograd MLP
Os conceitos de diferenciação automática (autograd) são diretamente estendidos para redes do tipo Perceptron Multicamadas (MLP, do inglês, Multilayer Perceptron). Uma MLP é uma composição de funções definidas por parâmetros (pesos e biases). Seu treinamento ocorre em duas etapas1010endnote: 10Para mais detalhes, consulte a Subseção 3.1.1.:
-
1.
Propagação (forward): os dados de entrada são propagados para todas as funções da rede, produzindo a saída estimada.
-
2.
Retropropagação (backward): a computação do gradiente do erro1111endnote: 11Medida da diferença entre o valor estimado e o valor esperado. em relação aos parâmetros da rede é realizado coletando as derivadas (gradientes) das funções da rede. Pela regra da cadeia, essa coleta é feita a partir da camada de saída em direção a camada de entrada da rede.
No seguinte exemplo, exploramos o fato de MLPs serem aproximadoras universais e avaliamos a derivada de uma MLP na aproximação de uma função.
Exemplo 3.4.3.
Vamos criar uma MLP
| (3.25) |
que aproxima a função
| (3.26) |
Em seguida, computamos, por diferenciação automática, o gradiente
| (3.27) |
e comparamos com o resultado esperado
| (3.28) |

3.4.2 Exercícios
E. 3.4.1.
Por diferenciação automática, compute o gradiente (a derivada) das seguintes funções
-
a)
para valores .
-
b)
para valores .
-
c)
para valores .
-
d)
para valores .
Em cada caso, compare os valores computados com os valores esperados.
E. 3.4.2.
Em cada item do Exercício 3.4.1, faça um fluxograma dos grafos computacionais da propagação e da retropropagação na computação dos gradientes.
E. 3.4.3.
Em cada item do Exercício 3.4.1, compute a derivada de segunda ordem da função indicada. Compare os valores computados com os valores esperados.
E. 3.4.4.
Por diferenciação automática, compute os gradientes das seguintes funções:
-
a)
para valores .
-
b)
para valores .
Em cada caso, compare os valores computados com os valores esperados.
E. 3.4.5.
Para as funções de cada item do Exercício 3.4.6, compute:
-
a)
.
-
b)
.
-
c)
.
Compare os valores computados com os valores esperados.
E. 3.4.6.
Em cada item do Exercício 3.4.6, compute o laplacino da função indicada. Compare os valores computados com os valores esperados.
E. 3.4.7.
Seja a função definida por
| (3.29) |
no domínio . Por diferenciação automática e para valores no domínio da função, compute:
-
a)
.
-
b)
.
-
c)
.
-
d)
.
-
e)
.
-
f)
.
-
g)
.
-
h)
.
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.