Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Pré-Cálculo
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
2.2 Inequações
Uma inequação é uma sentença matemática que expressa uma relação de desigualdade entre duas expressões matemáticas. São exemplos de inequações
| (2.77) | |||
| (2.78) | |||
| (2.79) | |||
| (2.80) | |||
| (2.81) |
Assim como equações, inequações são usadas para descrever propriedades ou restrições sobre uma ou mais incógnitas. Neste caso, a solução é o conjunto de valores que a incógnita pode assumir de forma a satisfazer a inequação.
Exemplo 2.2.1.
São exemplos de inequações envolvendo incógnitas:
-
a)
Inequação de primeiro grau
(2.82) -
b)
Inequação de segundo grau
(2.83) -
c)
Inequação racional
(2.84)
Não existe um procedimento geral para calcular a solução de uma inequação, mas o chamado estudo de sinal pode ser uma estratégia adequada em várias situações. Na sequência, vamos aplicá-la na resolução de algumas inequações.
2.2.1 Inequações de primeiro grau
Inequações de primeiro grau são aquelas em que a incógnita aparece apenas na potência 1. Ou seja, qualquer inequação que possa ser escrita na seguinte forma
| (2.85) |
onde , , são coeficientes/parâmetros dados e é a incógnita.
Para resolvê-la, podemos usar o estudo de sinal da expressão1919endnote: 19Lembremos a tricotomia dos números reais. Consulte a Subseção 1.3.3. . Para que seja nula, temos
| (2.86) |
Com isso, observamos que no caso de , temos que
| (2.87) |
e
| (2.88) |
Consultemos a Figura 2.1.


Exemplo 2.2.2.
Vamos resolver
| (2.91) |
Primeiramente, vamos reescrever a inequação no formato da (2.85). Para tanto, calculamos
| (2.92) | |||
| (2.93) | |||
| (2.94) |

Agora, fazemos o estudo de sinal de . Temos
| (2.95) |
Daí, segue que
| (2.96) |
e
| (2.97) |
Consulte a Figura 2.3. Logo, concluímos que a solução é .
Em alguns casos, é possível calcular a solução apenas a partir de manipulações algébricas.
Exemplo 2.2.3.
Vamos resolver
| (2.98) |
Começamos multiplicando ambos os lados da inequação por para obtermos2020endnote: 20Notemos que a desigualdade se inverte ao multiplicarmos a inequação por um número negativo.
| (2.99) |
Agora, multiplicamos por , como segue
| (2.100) | |||
| (2.101) |
Donde, temos a solução .
Verifique usando o SymPy!
2.2.2 Produtos ou quocientes
Inequações envolvendo produtos ou quocientes de expressões de primeiro grau podemos ser resolvidas fazendo-se o estudo de sinal.
Exemplo 2.2.4.
Vamos resolver
| (2.102) |
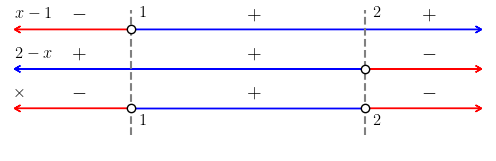
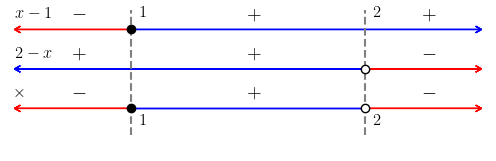
Para tanto, fazemos os estudos de sinais do primeiro fator e do segundo fator . Em seguida, fazemos o estudo de sinal do produto . Neste caso, obtemos a Figura 2.4. Com isso, temos que a solução é .
Verifique usando o SymPy!
No caso de quocientes, devemos nos atentar para o fato de que o denominador não seja nulo.
Exercícios
E. 2.2.1.
Resolva as seguintes inequações
-
a)
-
b)
-
c)
-
d)
Resposta 0.
a) ; b) ; c) ; d)
E. 2.2.2.
Resolva as seguintes inequações
-
1.
-
2.
-
3.
-
4.
Resposta 0.
a) ; b) ; c) ; d)
E. 2.2.3.
Resolva as seguintes inequações
-
1.
-
2.
-
3.
-
4.
Resposta 0.
a) ; b) ; c) ; d)
E. 2.2.4.
Resolva a seguinte inequação
| (2.104) |
Resposta 0.
E. 2.2.5.
Resolve a seguinte inequação
| (2.105) |
Resposta 0.
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.
Pré-Cálculo
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
2.2 Inequações
Uma inequação é uma sentença matemática que expressa uma relação de desigualdade entre duas expressões matemáticas. São exemplos de inequações
| (2.77) | |||
| (2.78) | |||
| (2.79) | |||
| (2.80) | |||
| (2.81) |
Assim como equações, inequações são usadas para descrever propriedades ou restrições sobre uma ou mais incógnitas. Neste caso, a solução é o conjunto de valores que a incógnita pode assumir de forma a satisfazer a inequação.
Exemplo 2.2.1.
São exemplos de inequações envolvendo incógnitas:
-
a)
Inequação de primeiro grau
(2.82) -
b)
Inequação de segundo grau
(2.83) -
c)
Inequação racional
(2.84)
Não existe um procedimento geral para calcular a solução de uma inequação, mas o chamado estudo de sinal pode ser uma estratégia adequada em várias situações. Na sequência, vamos aplicá-la na resolução de algumas inequações.
2.2.1 Inequações de primeiro grau
Inequações de primeiro grau são aquelas em que a incógnita aparece apenas na potência 1. Ou seja, qualquer inequação que possa ser escrita na seguinte forma
| (2.85) |
onde , , são coeficientes/parâmetros dados e é a incógnita.
Para resolvê-la, podemos usar o estudo de sinal da expressão1919endnote: 19Lembremos a tricotomia dos números reais. Consulte a Subseção 1.3.3. . Para que seja nula, temos
| (2.86) |
Com isso, observamos que no caso de , temos que
| (2.87) |
e
| (2.88) |
Consultemos a Figura 2.1.


Exemplo 2.2.2.
Vamos resolver
| (2.91) |
Primeiramente, vamos reescrever a inequação no formato da (2.85). Para tanto, calculamos
| (2.92) | |||
| (2.93) | |||
| (2.94) |

Agora, fazemos o estudo de sinal de . Temos
| (2.95) |
Daí, segue que
| (2.96) |
e
| (2.97) |
Consulte a Figura 2.3. Logo, concluímos que a solução é .
Em alguns casos, é possível calcular a solução apenas a partir de manipulações algébricas.
Exemplo 2.2.3.
Vamos resolver
| (2.98) |
Começamos multiplicando ambos os lados da inequação por para obtermos2020endnote: 20Notemos que a desigualdade se inverte ao multiplicarmos a inequação por um número negativo.
| (2.99) |
Agora, multiplicamos por , como segue
| (2.100) | |||
| (2.101) |
Donde, temos a solução .
Verifique usando o SymPy!
2.2.2 Produtos ou quocientes
Inequações envolvendo produtos ou quocientes de expressões de primeiro grau podemos ser resolvidas fazendo-se o estudo de sinal.
Exemplo 2.2.4.
Vamos resolver
| (2.102) |

Para tanto, fazemos os estudos de sinais do primeiro fator e do segundo fator . Em seguida, fazemos o estudo de sinal do produto . Neste caso, obtemos a Figura 2.4. Com isso, temos que a solução é .
Verifique usando o SymPy!
No caso de quocientes, devemos nos atentar para o fato de que o denominador não seja nulo.
Exercícios
E. 2.2.1.
Resolva as seguintes inequações
-
a)
-
b)
-
c)
-
d)
Resposta 0.
a) ; b) ; c) ; d)
E. 2.2.2.
Resolva as seguintes inequações
-
1.
-
2.
-
3.
-
4.
Resposta 0.
a) ; b) ; c) ; d)
E. 2.2.3.
Resolva as seguintes inequações
-
1.
-
2.
-
3.
-
4.
Resposta 0.
a) ; b) ; c) ; d)
E. 2.2.4.
Resolva a seguinte inequação
| (2.104) |
Resposta 0.
E. 2.2.5.
Resolve a seguinte inequação
| (2.105) |
Resposta 0.
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.