Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Pré-Cálculo
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
1.3 Conjunto dos números reais
1.3.1 Existência de números irracionais
Para introduzirmos os números reais, vamos fazer a tentativa de estender a operação de potenciação para potências racionais. Mais especificamente, vamos tentar determinar , a qual é definida por
| (1.105) |
Assumindo válidas as propriedades de potenciação vista para números racionais, teríamos
| (1.106) | |||
| (1.107) |
Será que é um número racional? Se fosse, então existiria uma razão irredutível88endnote: 8Sobre razão irredutível, consulte a Observação 1.2.10. tal que , e , com
| (1.108) | |||
| (1.109) | |||
| (1.110) |
Logo, é um número par99endnote: 9Número múltiplo inteiro de . e, portanto, é um número par1010endnote: 10O quadrado de um número ímpar é um número ímpar. Número ímpar é um número inteiro não divisível por .. Ou seja, existiria tal que . Mas, então
| (1.111) | |||
| (1.112) | |||
| (1.113) |
Com isso, seria par e, portanto, deveria ser par. Isso é uma contradição, por é uma razão irredutível. Logo, concluímos que
| (1.114) |
Assim sendo, dizemos que é um número irracional. Ou seja, não é racional! :D
Observação 1.3.1.
Uma aplicação em geometria. Observamos que é o comprimento do lado do quadrado de área 1. Ou ainda, é a hipotenusa do triângulo retângulo de catetos com comprimento igual a 1!
1.3.2 Fecho dos números racionais
Mas então, como podemos calcular o número ? Bem, podemos aproximá-lo usando o método babilônico. Observamos que é um número entre e , exclusivamente. Vamos, então, escolher como aproximação inicial
| (1.115) |
Daí, calculamos uma nova aproximação como
| (1.116) | |||
| (1.117) | |||
| (1.118) | |||
| (1.119) | |||
| (1.120) | |||
| (1.121) |
Então, analogamente podemos calcular uma melhor aproximação com
| (1.122) | |||
| (1.123) | |||
| (1.124) |
e assim sucessivamente. Estes números racionais estão de fato se aproximando do valor de . Notamos que
| (1.125) | |||
| (1.126) | |||
| (1.127) |
O método babilônico, nos mostra que pode ser calculado como o limite de uma sequência de números racionais. Ou seja, é sempre possível escolher um número racional que aproxime do valor de tão bem quanto se queira. No caso, basta iterarmos o método babilônico um número suficiente de vezes.
Neste caso, ainda dizemos que pertence ao fecho dos números racionais, escrevemos
| (1.128) |
Mais precisamente, quando sempre é possível escolher um número racional que aproxima o valor de tão bem quanto se queira.
O conjunto dos números reais é denotado por e é tal que
| (1.129) |
Ou seja, é a união dos números racionais com os números irracionais que podem ser arbitrariamente aproximados por números racionais.
Observação 1.3.2.
| (1.130) |
Além disso, os números reais herdam as operações e suas propriedades dos números racionais.
Exemplo 1.3.1.
Consideramos os seguintes casos:
-
a)
todo número inteiro é um número real.
-
b)
todo número racional é um número real.
-
c)
são números reais.
-
d)
é um número real.
O é a área da circunferência de raio 1.
De posse dos números reais, vamos definir -ésima raiz de um número por
| (1.131) |
sendo que quando , escrevermos simplesmente .
Observação 1.3.3.
| (1.132) |
De fato, seja
| (1.133) |
então
| (1.134) |
Entretanto, o quadrado de qualquer número real é um número não negativo! Ou seja, .
Mais geralmente, não é número real a raiz de índice par de qualquer número negativo.
1.3.3 Reta real
A reta real é uma representação geométrica do conjunto dos números reais (Figura 1.2).
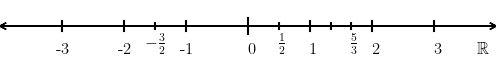
Traçamos uma reta horizontal e escolhemos um ponto como sendo a origem. Neste ponto, marcamos a posição do número zero. Usando um espaçamento fixo, posicionamos os números naturais a direita do zero e de forma sucessiva. Os números inteiros negativos são posicionados à esquerda do zero, também em posições sucessivas. Os números racionais são posicionados tomando as frações do espaçamento escolhido. A Figura 1.2 é um esboço da reta real.
Uma das propriedades notáveis dos números reais é a chamada tricotomia, i.e. um número real é
-
•
positivo (posicionado à direita da origem),
-
•
zero (posicionado na origem), ou
-
•
negativo (posicionado à esquerda da origem),
exclusivamente.
1.3.4 Infinito
O infinito é denotado por e representa a noção daquilo que não tem fim. Quando sem sinal, é interpretado na direção positiva (direita) da reta real. Quando escrito (lê-se menos infinito) é interpretado na direção negativa (esquerda) da reta real. Nesta reta (Fig. 1.3), é representado por sua seta à direta e por sua seta à esquerda.
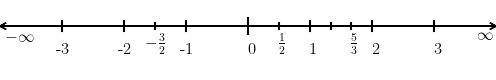
Observação 1.3.4.
não é um número!
Sendo é um número real, podemos inferir as seguintes propriedades para qualquer dado :
-
•
-
•
-
•
-
•
,
-
•
,
-
•
-
•
-
•
Exemplo 1.3.2.
Estudamos os seguintes casos:
-
a)
-
b)
-
c)
-
d)
-
e)
No entanto, são consideradas indeterminações matemáticas as seguintes operações:
-
•
-
•
-
•
-
•
-
•
-
•
-
•
Observação 1.3.5.
Com o SymPy, as indeterminações são marcadas como nan1111endnote: 11Do inglês, not a number. ou retornam erro. Por exemplo:
Atenção! Exceções são os casos envolvendo potências de expoente , por exemplo:
1.3.5 Intervalos de números reais
Intervalos de números reais são conjuntos especiais e muito utilizados. Por simplicidade, recebem uma notação própria. Para , temos os seguintes tipos de intervalos:
-
•
Intervalo fechado
(1.135) 
Figura 1.4: Representação geométrica de um intervalo . -
•
Intervalo semi-aberto à esquerda (semi-fechado à direita)
(1.136) 
Figura 1.5: Representação geométrica de um intervalo . -
•
Intervalo semi-aberto à direita (semi-fechado à esquerda)
(1.137) 
Figura 1.6: Representação geométrica de um intervalo . -
•
Intervalo aberto
(1.138) 
Figura 1.7: Representação geométrica de um intervalo .
Exemplo 1.3.3.
Vamos estudar os seguintes casos:
-
a)
-
b)
-
c)
-
d)
-
e)
-
f)
-
g)
Com o SymPy, podemos checar os casos acima usando o comando Interval. Vejamos alguns dos casos acima:
Ainda, temos os seguintes casos especiais
-
•
Intervalos semi-limitados à esquerda
(1.139) 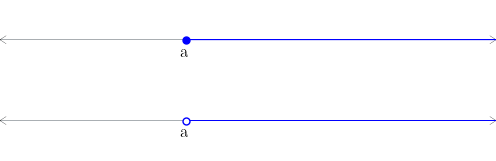
Figura 1.8: Representação geométrica dos intervalos (acima) e (abaixo). -
•
Intervalos semi-limitados à direita
(1.140) 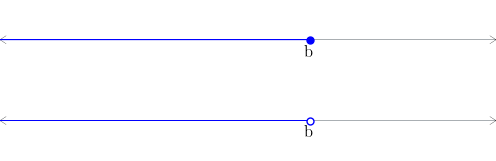
Figura 1.9: Representação geométrica dos intervalos (acima) e (abaixo). -
•
Intervalo ilimitado
(1.141) 
Figura 1.10: Representação geométrica dos intervalos .
Exemplo 1.3.4.
Estudamos os seguintes casos:
-
a)
-
b)
-
c)
-
d)
-
e)
Com o Python, podemos fazer estas verificações com os seguintes comandos:
Exercícios
E. 1.3.1.
Verifique a veracidade de cada uma das seguintes afirmações. Justifique sua resposta.
-
a)
Se são números pares, então é um número par.
-
b)
Se são números ímpares, então é um número ímpar.
-
c)
Se é número par e é número ímpar, então é número ímpar.
-
d)
Se é número par e é número ímpar, então é número ímpar.
-
e)
Se são números ímpares, então é número ímpar.
Resposta 0.
a) V; b) F; c) V; d) F; e) V
E. 1.3.2.
Mostre que .
E. 1.3.3.
Um número primo tem somente quatro divisores , e é tal que e . Faça a decomposição em fatores primos dos seguintes números1212endnote: 12Dica: consulte o método sympy.factorint..
-
a)
-
b)
-
c)
-
d)
Resposta 0.
a) ; b) ; c) ; d)
E. 1.3.4.
Encontre o resultado e faça a representação gráfica em cada um dos seguintes itens.
-
1.
-
2.
-
3.
-
4.
-
5.
Resposta 0.
a) , b) ; c) ; d) ; e)
E. 1.3.5.
Verifique a veracidade de cada uma das seguintes afirmações. Justifique sua resposta.
-
a)
-
b)
-
c)
-
d)
-
e)
Resposta 0.
a) F; b) V; c) V; d) V; e) F
E. 1.3.6.
Mostre que1313endnote: 13, e , caso contrário. .
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.
Pré-Cálculo
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
1.3 Conjunto dos números reais
1.3.1 Existência de números irracionais
Para introduzirmos os números reais, vamos fazer a tentativa de estender a operação de potenciação para potências racionais. Mais especificamente, vamos tentar determinar , a qual é definida por
| (1.105) |
Assumindo válidas as propriedades de potenciação vista para números racionais, teríamos
| (1.106) | |||
| (1.107) |
Será que é um número racional? Se fosse, então existiria uma razão irredutível88endnote: 8Sobre razão irredutível, consulte a Observação 1.2.10. tal que , e , com
| (1.108) | |||
| (1.109) | |||
| (1.110) |
Logo, é um número par99endnote: 9Número múltiplo inteiro de . e, portanto, é um número par1010endnote: 10O quadrado de um número ímpar é um número ímpar. Número ímpar é um número inteiro não divisível por .. Ou seja, existiria tal que . Mas, então
| (1.111) | |||
| (1.112) | |||
| (1.113) |
Com isso, seria par e, portanto, deveria ser par. Isso é uma contradição, por é uma razão irredutível. Logo, concluímos que
| (1.114) |
Assim sendo, dizemos que é um número irracional. Ou seja, não é racional! :D
Observação 1.3.1.
Uma aplicação em geometria. Observamos que é o comprimento do lado do quadrado de área 1. Ou ainda, é a hipotenusa do triângulo retângulo de catetos com comprimento igual a 1!
1.3.2 Fecho dos números racionais
Mas então, como podemos calcular o número ? Bem, podemos aproximá-lo usando o método babilônico. Observamos que é um número entre e , exclusivamente. Vamos, então, escolher como aproximação inicial
| (1.115) |
Daí, calculamos uma nova aproximação como
| (1.116) | |||
| (1.117) | |||
| (1.118) | |||
| (1.119) | |||
| (1.120) | |||
| (1.121) |
Então, analogamente podemos calcular uma melhor aproximação com
| (1.122) | |||
| (1.123) | |||
| (1.124) |
e assim sucessivamente. Estes números racionais estão de fato se aproximando do valor de . Notamos que
| (1.125) | |||
| (1.126) | |||
| (1.127) |
O método babilônico, nos mostra que pode ser calculado como o limite de uma sequência de números racionais. Ou seja, é sempre possível escolher um número racional que aproxime do valor de tão bem quanto se queira. No caso, basta iterarmos o método babilônico um número suficiente de vezes.
Neste caso, ainda dizemos que pertence ao fecho dos números racionais, escrevemos
| (1.128) |
Mais precisamente, quando sempre é possível escolher um número racional que aproxima o valor de tão bem quanto se queira.
O conjunto dos números reais é denotado por e é tal que
| (1.129) |
Ou seja, é a união dos números racionais com os números irracionais que podem ser arbitrariamente aproximados por números racionais.
Observação 1.3.2.
| (1.130) |
Além disso, os números reais herdam as operações e suas propriedades dos números racionais.
Exemplo 1.3.1.
Consideramos os seguintes casos:
-
a)
todo número inteiro é um número real.
-
b)
todo número racional é um número real.
-
c)
são números reais.
-
d)
é um número real.
O é a área da circunferência de raio 1.
De posse dos números reais, vamos definir -ésima raiz de um número por
| (1.131) |
sendo que quando , escrevermos simplesmente .
Observação 1.3.3.
| (1.132) |
De fato, seja
| (1.133) |
então
| (1.134) |
Entretanto, o quadrado de qualquer número real é um número não negativo! Ou seja, .
Mais geralmente, não é número real a raiz de índice par de qualquer número negativo.
1.3.3 Reta real
A reta real é uma representação geométrica do conjunto dos números reais (Figura 1.2).
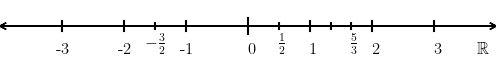
Traçamos uma reta horizontal e escolhemos um ponto como sendo a origem. Neste ponto, marcamos a posição do número zero. Usando um espaçamento fixo, posicionamos os números naturais a direita do zero e de forma sucessiva. Os números inteiros negativos são posicionados à esquerda do zero, também em posições sucessivas. Os números racionais são posicionados tomando as frações do espaçamento escolhido. A Figura 1.2 é um esboço da reta real.
Uma das propriedades notáveis dos números reais é a chamada tricotomia, i.e. um número real é
-
•
positivo (posicionado à direita da origem),
-
•
zero (posicionado na origem), ou
-
•
negativo (posicionado à esquerda da origem),
exclusivamente.
1.3.4 Infinito
O infinito é denotado por e representa a noção daquilo que não tem fim. Quando sem sinal, é interpretado na direção positiva (direita) da reta real. Quando escrito (lê-se menos infinito) é interpretado na direção negativa (esquerda) da reta real. Nesta reta (Fig. 1.3), é representado por sua seta à direta e por sua seta à esquerda.
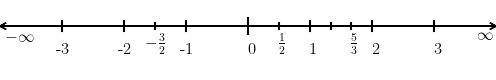
Observação 1.3.4.
não é um número!
Sendo é um número real, podemos inferir as seguintes propriedades para qualquer dado :
-
•
-
•
-
•
-
•
,
-
•
,
-
•
-
•
-
•
Exemplo 1.3.2.
Estudamos os seguintes casos:
-
a)
-
b)
-
c)
-
d)
-
e)
No entanto, são consideradas indeterminações matemáticas as seguintes operações:
-
•
-
•
-
•
-
•
-
•
-
•
-
•
Observação 1.3.5.
Com o SymPy, as indeterminações são marcadas como nan1111endnote: 11Do inglês, not a number. ou retornam erro. Por exemplo:
Atenção! Exceções são os casos envolvendo potências de expoente , por exemplo:
1.3.5 Intervalos de números reais
Intervalos de números reais são conjuntos especiais e muito utilizados. Por simplicidade, recebem uma notação própria. Para , temos os seguintes tipos de intervalos:
-
•
Intervalo fechado
(1.135) 
Figura 1.4: Representação geométrica de um intervalo . -
•
Intervalo semi-aberto à esquerda (semi-fechado à direita)
(1.136) 
Figura 1.5: Representação geométrica de um intervalo . -
•
Intervalo semi-aberto à direita (semi-fechado à esquerda)
(1.137) 
Figura 1.6: Representação geométrica de um intervalo . -
•
Intervalo aberto
(1.138) 
Figura 1.7: Representação geométrica de um intervalo .
Exemplo 1.3.3.
Vamos estudar os seguintes casos:
-
a)
-
b)
-
c)
-
d)
-
e)
-
f)
-
g)
Com o SymPy, podemos checar os casos acima usando o comando Interval. Vejamos alguns dos casos acima:
Ainda, temos os seguintes casos especiais
-
•
Intervalos semi-limitados à esquerda
(1.139) 
Figura 1.8: Representação geométrica dos intervalos (acima) e (abaixo). -
•
Intervalos semi-limitados à direita
(1.140) 
Figura 1.9: Representação geométrica dos intervalos (acima) e (abaixo). -
•
Intervalo ilimitado
(1.141) 
Figura 1.10: Representação geométrica dos intervalos .
Exemplo 1.3.4.
Estudamos os seguintes casos:
-
a)
-
b)
-
c)
-
d)
-
e)
Com o Python, podemos fazer estas verificações com os seguintes comandos:
Exercícios
E. 1.3.1.
Verifique a veracidade de cada uma das seguintes afirmações. Justifique sua resposta.
-
a)
Se são números pares, então é um número par.
-
b)
Se são números ímpares, então é um número ímpar.
-
c)
Se é número par e é número ímpar, então é número ímpar.
-
d)
Se é número par e é número ímpar, então é número ímpar.
-
e)
Se são números ímpares, então é número ímpar.
Resposta 0.
a) V; b) F; c) V; d) F; e) V
E. 1.3.2.
Mostre que .
E. 1.3.3.
Um número primo tem somente quatro divisores , e é tal que e . Faça a decomposição em fatores primos dos seguintes números1212endnote: 12Dica: consulte o método sympy.factorint..
-
a)
-
b)
-
c)
-
d)
Resposta 0.
a) ; b) ; c) ; d)
E. 1.3.4.
Encontre o resultado e faça a representação gráfica em cada um dos seguintes itens.
-
1.
-
2.
-
3.
-
4.
-
5.
Resposta 0.
a) , b) ; c) ; d) ; e)
E. 1.3.5.
Verifique a veracidade de cada uma das seguintes afirmações. Justifique sua resposta.
-
a)
-
b)
-
c)
-
d)
-
e)
Resposta 0.
a) F; b) V; c) V; d) V; e) F
E. 1.3.6.
Mostre que1313endnote: 13, e , caso contrário. .
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.