Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Pré-Cálculo
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
3.9 Funções exponenciais
Uma função exponencial tem a forma
| (3.153) |
onde é uma constante positiva e é chamada de base da função exponencial.
Funções exponenciais estão definidas em toda parte e têm imagem . O gráfico de uma função exponencial sempre contém os pontos , e . Veja a Figura 3.37.
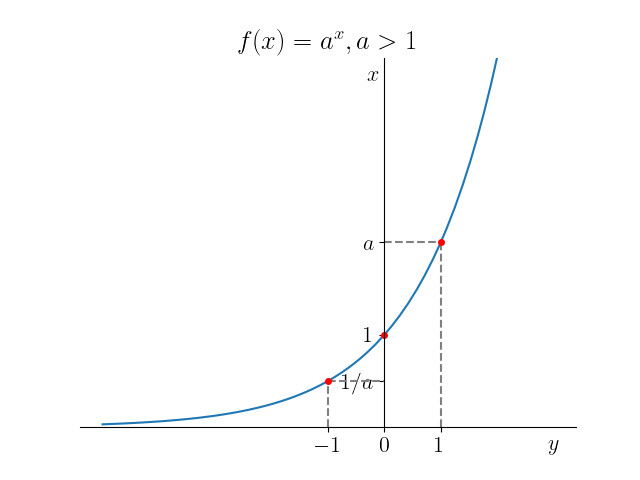
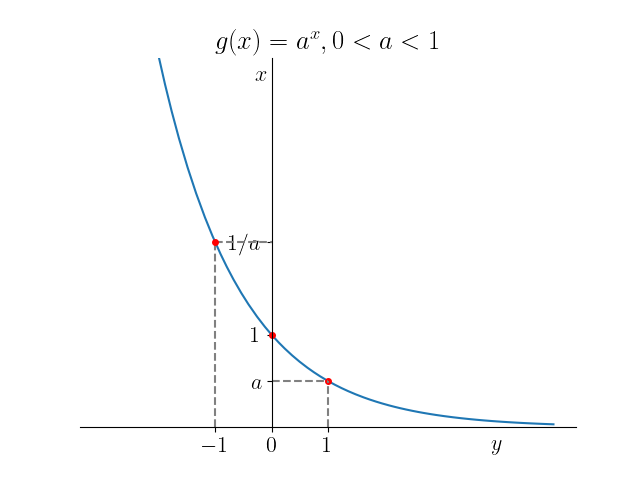
Observação 3.9.1.
Quando a base é o Número de Euler3333endnote: 33Leonhard Paul Euler, 1707 - 1783, matemático e físico suíço. Fonte: Wikipédia.
| (3.154) |
chamamos de função exponencial (natural).
Exemplo 3.9.1.
Vamos estudar os gráficos cada uma das seguintes funções exponenciais:
-
a)
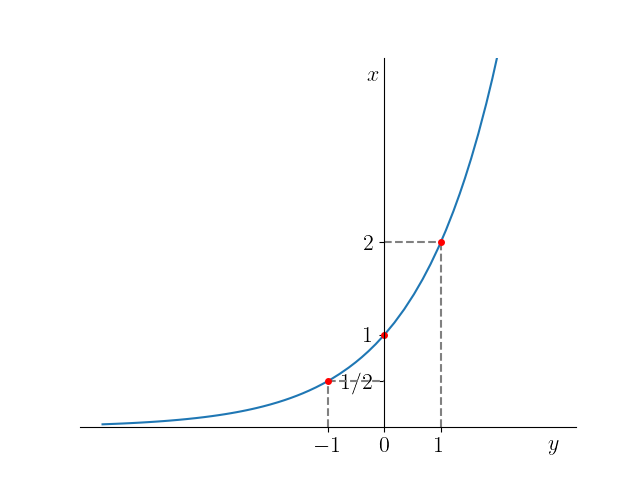
Figura 3.38: Esboço do gráfico da função . -
b)
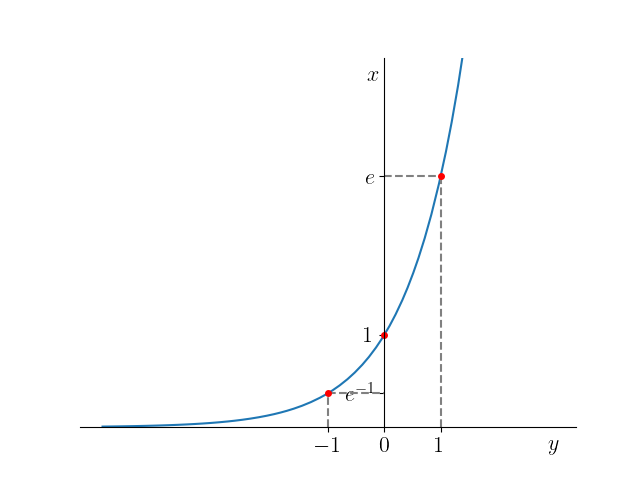
Figura 3.39: Esboço do gráfico da função . -
c)
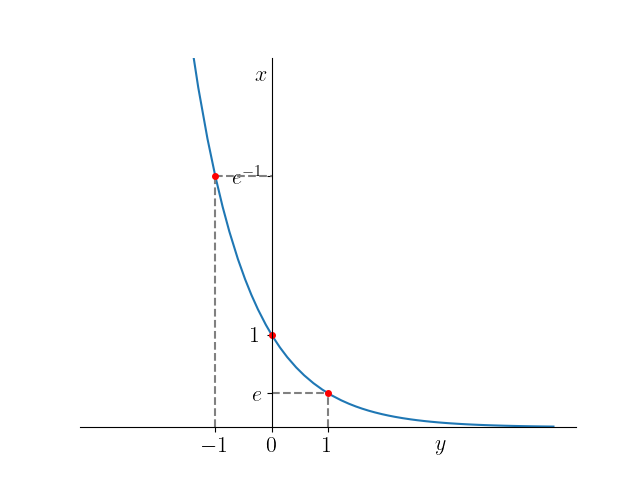
Figura 3.40: Esboço do gráfico da função .
Exercícios resolvidos
ER 3.9.1.
Faça um esboço do gráfico de .
Solução 0.
Primeiramente, observamos que
| (3.155) | ||||
| (3.156) |
Então, partindo do gráfico de , fazemos uma translação de unidades à direita, seguida de uma contração horizontal de vezes e, por fim, uma translação para baixo de uma unidade. Consulte as Figuras 3.41-3.43.
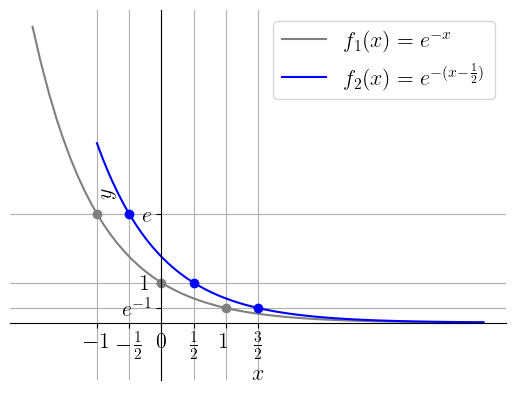
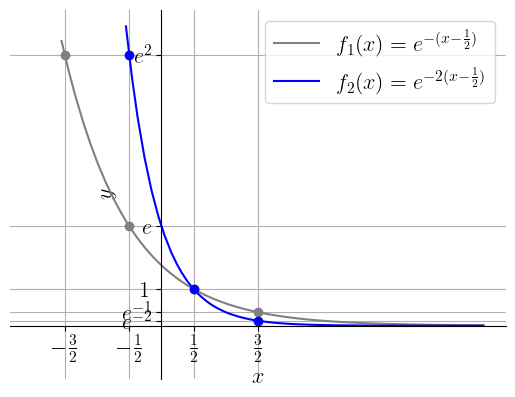
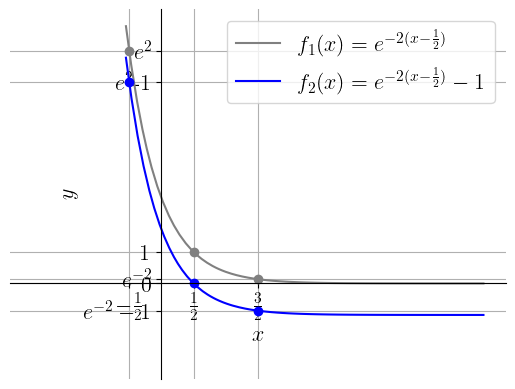
ER 3.9.2.
Calcule o(s) zero(s) da seguinte função
| (3.157) |
Solução 0.
Um zero da função é um ponto onde
| (3.158) | |||
| (3.159) | |||
| (3.160) |
Para resolver esta equação exponencial, lembramos que . Logo, temos
| (3.161) | |||
| (3.162) | |||
| (3.163) |
Concluímos que é o único zero da função.
Exercícios
E. 3.9.1.
Faça um esboço do gráfico de cada uma das seguintes funções:
-
a)
-
b)
-
c)
-
d)
Resposta 0.
Dica: use um pacote de matemática simbólica para verificar suas respostas.
E. 3.9.2.
Justificando, determine a veracidade das seguintes afirmações:
-
a)
é uma função crescente;
-
b)
é uma função decrescente;
-
c)
é uma função decrescente;
-
d)
para todo .
Resposta 0.
a) V; b) V; c) F; d) V
E. 3.9.3.
Calcule o zero da função
| (3.164) |
Resposta 0.
E. 3.9.4.
Faça um esboço do gráfico de .
Resposta 0.
Dica: use um pacote de matemática simbólica para verificar sua resposta.
E. 3.9.5.
(Aplicação.) Na física química, a Equação de Arrhenius3535endnote: 35Svante August Arrhenius, 1859-1927, químico sueco. Fonte: Wikipédia. fornece a taxa de reação (entre espécies químicas) em função da temperatura [K]
| (3.165) |
onde é o fator constante pré-exponencial, é a energia de ativação e é a constante universal dos gases. Para temperatura constante, a equação acima define a função . Em relação a esta função, responda cada um dos seguintes itens:
-
a)
A função é crescente ou decrescente? E, o que isso significa?
-
b)
Determine o domínio da função . O que ele significa na aplicação.
-
c)
Determine a imagem da função . O que ela significa na aplicação.
-
d)
Faça um esboço do gráfico da função .
Resposta 0.
a) Decrescente. Significa que quanto maior a energia de ativação, menor é a taxa de reação. b) , são os possíveis valores para a energia de ativação. c) , significa que a taxa de reação é sempre um valor entre 0 e A, exclusivamente.
E. 3.9.6.
(Aplicação.) Uma das técnicas de inteligência artificial consiste em utilizar de neurônios artificiais3636endnote: 36Modelos matemáticos baseados em neurônios biológicos.. A saída fornecida por um neurônio depende da escolha da chamada função de ativação . Em muitas aplicações, a função logística é escolhida, i.e.
| (3.166) |
Responda cada um dos seguintes itens:
-
a)
Escreva essa função de ativação como uma composição de duas funções e .
-
b)
Determine o domínio dessa função de ativação .
-
c)
Determine a imagem dessa função de ativação .
Resposta 0.
a) , , ; b) ; c) .
E. 3.9.7.
(Aplicação.) O fenômeno de desintegração espontânea do núcleo de um átomo com a emissão de algumas radiações é chamado de radioatividade3737endnote: 37Fonte: Wikipédia.. A lei fundamental do decaimento radiativo estabelece que a taxa de decaimento é proporcional ao número de átomos que ainda não decaíram. Isto nos fornece a equação da lei básica da radioatividade
| (3.167) |
onde, é o número de átomos no tempo , é o número de átomos presentes no tempo inicial e é a constante de decaimento. Faça o esboço do gráfico da função .
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.
Pré-Cálculo
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
3.9 Funções exponenciais
Uma função exponencial tem a forma
| (3.153) |
onde é uma constante positiva e é chamada de base da função exponencial.
Funções exponenciais estão definidas em toda parte e têm imagem . O gráfico de uma função exponencial sempre contém os pontos , e . Veja a Figura 3.37.


Observação 3.9.1.
Quando a base é o Número de Euler3333endnote: 33Leonhard Paul Euler, 1707 - 1783, matemático e físico suíço. Fonte: Wikipédia.
| (3.154) |
chamamos de função exponencial (natural).
Exemplo 3.9.1.
Vamos estudar os gráficos cada uma das seguintes funções exponenciais:
-
a)

Figura 3.38: Esboço do gráfico da função . -
b)

Figura 3.39: Esboço do gráfico da função . -
c)

Figura 3.40: Esboço do gráfico da função .
Exercícios resolvidos
ER 3.9.1.
Faça um esboço do gráfico de .
Solução 0.
Primeiramente, observamos que
| (3.155) | ||||
| (3.156) |
Então, partindo do gráfico de , fazemos uma translação de unidades à direita, seguida de uma contração horizontal de vezes e, por fim, uma translação para baixo de uma unidade. Consulte as Figuras 3.41-3.43.



ER 3.9.2.
Calcule o(s) zero(s) da seguinte função
| (3.157) |
Solução 0.
Um zero da função é um ponto onde
| (3.158) | |||
| (3.159) | |||
| (3.160) |
Para resolver esta equação exponencial, lembramos que . Logo, temos
| (3.161) | |||
| (3.162) | |||
| (3.163) |
Concluímos que é o único zero da função.
Exercícios
E. 3.9.1.
Faça um esboço do gráfico de cada uma das seguintes funções:
-
a)
-
b)
-
c)
-
d)
Resposta 0.
Dica: use um pacote de matemática simbólica para verificar suas respostas.
E. 3.9.2.
Justificando, determine a veracidade das seguintes afirmações:
-
a)
é uma função crescente;
-
b)
é uma função decrescente;
-
c)
é uma função decrescente;
-
d)
para todo .
Resposta 0.
a) V; b) V; c) F; d) V
E. 3.9.3.
Calcule o zero da função
| (3.164) |
Resposta 0.
E. 3.9.4.
Faça um esboço do gráfico de .
Resposta 0.
Dica: use um pacote de matemática simbólica para verificar sua resposta.
E. 3.9.5.
(Aplicação.) Na física química, a Equação de Arrhenius3535endnote: 35Svante August Arrhenius, 1859-1927, químico sueco. Fonte: Wikipédia. fornece a taxa de reação (entre espécies químicas) em função da temperatura [K]
| (3.165) |
onde é o fator constante pré-exponencial, é a energia de ativação e é a constante universal dos gases. Para temperatura constante, a equação acima define a função . Em relação a esta função, responda cada um dos seguintes itens:
-
a)
A função é crescente ou decrescente? E, o que isso significa?
-
b)
Determine o domínio da função . O que ele significa na aplicação.
-
c)
Determine a imagem da função . O que ela significa na aplicação.
-
d)
Faça um esboço do gráfico da função .
Resposta 0.
a) Decrescente. Significa que quanto maior a energia de ativação, menor é a taxa de reação. b) , são os possíveis valores para a energia de ativação. c) , significa que a taxa de reação é sempre um valor entre 0 e A, exclusivamente.
E. 3.9.6.
(Aplicação.) Uma das técnicas de inteligência artificial consiste em utilizar de neurônios artificiais3636endnote: 36Modelos matemáticos baseados em neurônios biológicos.. A saída fornecida por um neurônio depende da escolha da chamada função de ativação . Em muitas aplicações, a função logística é escolhida, i.e.
| (3.166) |
Responda cada um dos seguintes itens:
-
a)
Escreva essa função de ativação como uma composição de duas funções e .
-
b)
Determine o domínio dessa função de ativação .
-
c)
Determine a imagem dessa função de ativação .
Resposta 0.
a) , , ; b) ; c) .
E. 3.9.7.
(Aplicação.) O fenômeno de desintegração espontânea do núcleo de um átomo com a emissão de algumas radiações é chamado de radioatividade3737endnote: 37Fonte: Wikipédia.. A lei fundamental do decaimento radiativo estabelece que a taxa de decaimento é proporcional ao número de átomos que ainda não decaíram. Isto nos fornece a equação da lei básica da radioatividade
| (3.167) |
onde, é o número de átomos no tempo , é o número de átomos presentes no tempo inicial e é a constante de decaimento. Faça o esboço do gráfico da função .
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.