Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Matemática Numérica III
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
1.1 Matrizes Esparsas
Em revisão
Uma matriz é dita ser esparsa quando ela tem apenas poucos elementos não nulos. A ideia é que os elementos não nulos não precisam ser guardados na memória do computador, gerando um grande benefício na redução da demanda de armazenamento de dados. O desafio está no desenvolvimento de estruturas de dados para a alocação eficiente de tais matrizes, i.e. que sejam suficientemente adequadas para os métodos numéricos conhecidos.
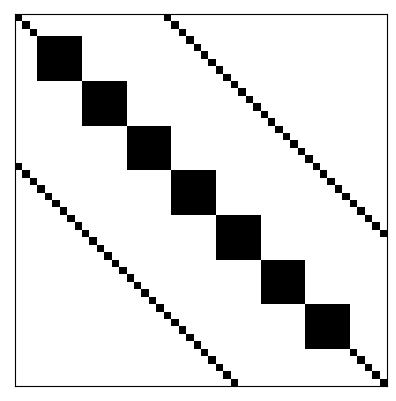
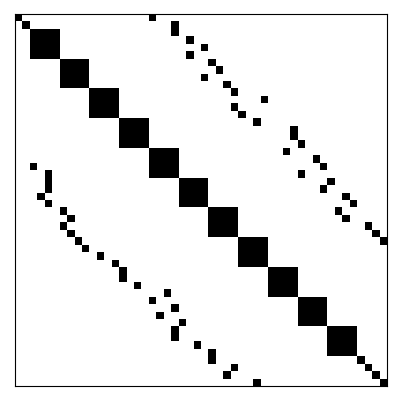
Matrizes esparsas podem ser classificadas como estruturadas ou não-estruturadas. Uma matriz estruturada é aquela em que as entradas não-nulas formam um padrão regular. Por exemplo, estão dispostas em poucas diagonais ou formam blocos (submatrizes densas) ao longo de sua diagonal principal. No caso de não haver um padrão regular das entradas não-nulas, a matriz esparsa é dita ser não-estruturada. Consulte a Figura 1.1 para exemplos.
A esparsidade de uma matriz é a porcentagem de elementos nulos que ela tem, i.e. para uma matriz quadrada tem-se que a esparsidade é
| (1.1) |
Por exemplo, a matriz identidade de tamanho tem esparsidade
| (1.2) |
1.1.1 Sistemas Tridiagonais
Em revisão
Um sistema tridiagonal tem a seguinte forma matricial
| (1.3) |
Ou seja, é um sistema cuja a matriz dos coeficientes é tridiagonal.
Uma matriz tridiagonal é uma matriz esparsa estruturada. Mais especificamente, é um caso particular de uma matriz banda, em que os elementos não nulos estão dispostos apenas em algumas de suas diagonais. Para armazenarmos tal matriz precisamos alocar apenas os seguintes três vetores
| (1.4) | |||
| (1.5) | |||
| (1.6) |
Ou seja, precisamos armazenar pontos flutuantes em vez de , como seria o caso se a matriz dos coeficientes fosse densa. Com isso, podemos alocar a matriz do sistema da seguinte forma
| (1.7) |
Ou seja, , sendo
| (1.8) |
Exemplo 1.1.1.
Seja o seguinte sistema linear
| (1.9) | |||
| (1.10) | |||
| (1.11) |
O seguinte código Python faz a alocação de seu vetor dos termos constantes e de sua matriz de coeficientes no formato compacto de .
Algoritmo de Thomas (TDMA)
Em revisão
O algoritmo de Thomas11endnote: 1Llewellyn Hilleth Thomas, 1903 - 1992, físico e matemático aplicado britânico. Fonte: Wikipedia. ou TDMA (do inglês, Tridiagonal Matrix Algorithm) é uma forma otimizada do método de eliminação gaussiana22endnote: 2Johann Carl Friedrich Gauss, 1777 - 1855, matemático alemão. Fonte: Wikipédia: Carl Friedrich Gauss. aplicada a sistemas tridiagonais. Enquanto este requer operações, esse demanda apenas .
Eliminando os termos abaixo da diagonal em (1.3), obtemos o sistema equivalente
| (1.12) |
Este é obtido pela seguinte iteração
| (1.13) | |||
| (1.14) | |||
| (1.15) |
onde, o ~ foi esquecido de propósito, indicando a reutilização da matriz e do vetor . A solução do sistema é, então, obtida de baixo para cima, i.e.
| (1.16) | |||
| (1.17) |
com .
1.1.2 Matrizes Banda
Em revisão
Uma matriz banda é aquela em que os elementos não nulos estão dispostos em apenas algumas de suas diagonais. Consulte a Figura 1.2.

Exemplo 1.1.2.
Consideramos o seguinte problema de Poisson33endnote: 3Siméon Denis Poisson, 1781 - 1840, matemático francês. Fonte: Wikipédia:Siméon Denis Poisson.
| (1.18) | |||
| (1.19) | |||
| (1.20) | |||
| (1.21) | |||
| (1.22) |
onde, é o operador laplaciano44endnote: 4Pierre-Simon Laplace, 1749 - 1827, matemático francês. Fonte: Wikipédia: Pierre-Simon Laplace.. Para fixarmos as ideias, vamos assumir
| (1.23) |
Vamos empregar o método de diferenças finitas para computar uma aproximação para a sua solução. Começamos assumindo uma malha uniforme de nodos
| (1.24) | |||
| (1.25) |
com tamanho de malha , e . Empregando a fórmula de diferenças central, encontramos o seguinte problema discreto associado
| (1.26) | |||
| (1.27) | |||
| (1.28) |
Este é um sistema linear . Tomando em conta as condições de contorno, ele pode ser reduzido a um sistema
| (1.29) |
usando a enumeração das incógnitas
| (1.30) |
i.e.
| (1.31) |
para . Consulte a Figura 1.3 para uma representação da enumeração em relação a malha.
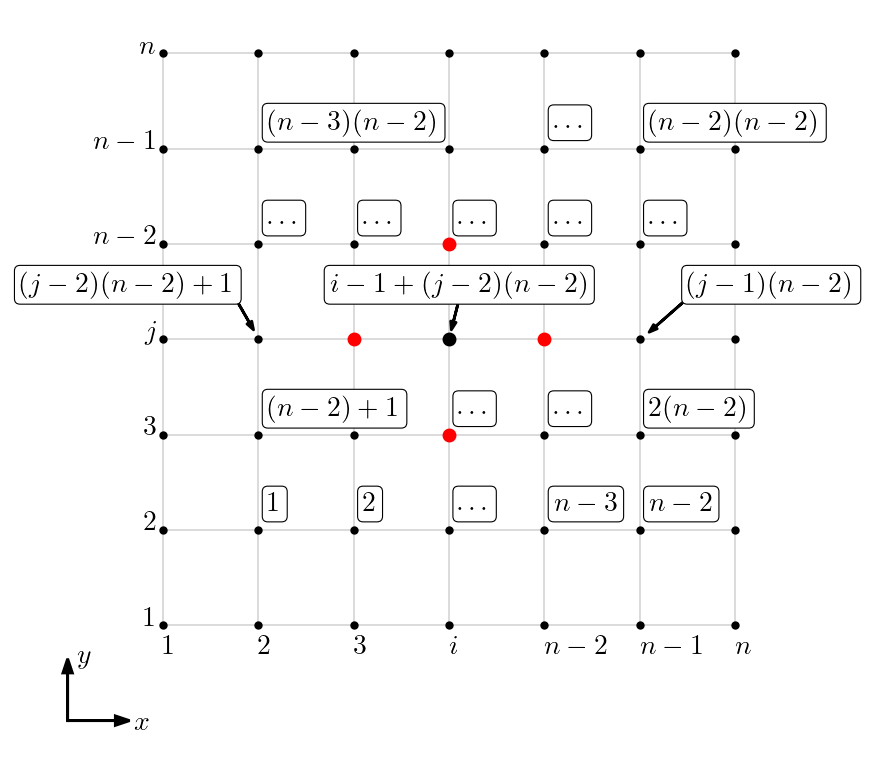
Afim de obtermos uma matriz diagonal dominante, vamos ordenar as equações do sistema discreto como segue
-
•
, :
(1.32) -
•
, :
(1.33) -
•
, :
(1.34) -
•
, :
(1.35) -
•
, :
(1.36) -
•
, :
(1.37) -
•
, :
(1.38) -
•
, :
(1.39) -
•
, :
(1.40)
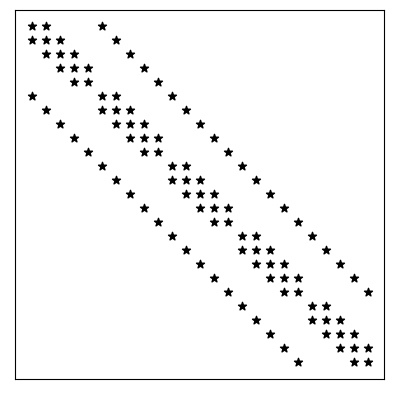
Com isso, temos um sistema com matriz com 5 bandas, consulte a Figura 1.4.
1.1.3 Esquemas de Armazenamento
Em revisão
A ideia é armazenar apenas os elementos não-nulos de uma matriz esparsa, de forma a economizar a demanda de armazenamento computacional. Cuidados devem ser tomados para que a estrutura de armazenamento utilizada seja adequada para a computação das operações matriciais mais comuns.
Formato COO
Em revisão
O formato COO (do inglês, COOrdinate format) é o esquema de armazenamento simples de matrizes esparsas. As estrutura de dados consiste em três arranjos:
-
1.
um arranjo contendo as entradas não-nulas da matriz;
-
2.
um arranjo contendo seus índices de linha;
-
3.
um arranjo contendo seus índices de coluna.
O método scipy.sparse.coo_array permite a alocação de matrizes no formato COO.
Exemplo 1.1.3.
O seguinte código armazena a matriz
| (1.41) |
no formato COO.
Vantagens do formato COO
-
•
Permite a entrada de dados duplicados (simplicidade).
-
•
Conversão rápida para os formatos CSR e CSC55endnote: 5CSR e CSC são formatos de matrizes esparsas mais eficientes para a computação matricial..
Desavantagens do formato COO
-
•
complexidade em operações aritméticas.
-
•
complexidade na extração de submatrizes.
Observação 1.1.1.
(Entradas Duplicadas.) O formato COO permite a entrada duplicada de elementos da matriz. Na conversão para outros formatos (por exemplo, CSR ou CSC), as entradas duplicadas são somadas.
Formato CSR
Em revisão
O formato CSR (do inglês, Compressed Sparse Row) é uma variação do COO que busca diminuir a alocação de dados repetidos. Assim como o COO, o formato conta com três arranjos , , :
-
•
é o arranjo contendo os elementos não-nulos da matriz, ordenados por linhas (i.e., da esquerda para direita, de cima para baixo);
-
•
é o arranjo contendo o índice das colunas das entradas não-nulas da matriz (como no formato COO);
-
•
é um arranjo cujos elementos são a posição no arranjo em que cada linha da matriz começa a ser representada. O número de elementos de -ésima linha da matriz dado por .
O método scipy.sparse.csr_array permite a alocação de matrizes no formato CSR.
Exemplo 1.1.4.
No Exemplo 1.1.3, alocamos a matriz
| (1.42) |
no formato COO. Aqui, vamos converter a alocação para o formato CSR e, então, verificar seus atributos.
d = [ 2. 1. 3. 2. -1. -1. -2. 1.] c = [0 2 1 2 3 1 2 3] p = [0 2 5 7 8]
Por exemplo, o elemento p[i=2] = 5 aponta para o c[k=5] = 1, o que fornece A[i=2,j=1] = d[k] = -1.. Verifique!
Vantagens do formato CSR
-
•
operações aritméticas eficientes;
-
•
fatiamento por linhas eficiente;
-
•
multiplicação matriz vetor eficiente.
Desvantagens do formato CSR
-
•
fatiamento por colunas não eficiente;
-
•
custo elevado de realocamento com alteração da esparsidade da matriz.
Formato CSC
Em revisão
O formato CSC (do inglês, Compressed Sparse Column) é uma variação análoga do CSR, mas para armazenamento por colunas. O formato conta com três arranjos , , :
-
•
é o arranjo contendo os elementos não-nulos da matriz, ordenados por colunas (i.e., de cima para baixo, da esquerda para direita);
-
•
é o arranjo contendo o índice das linhas das entradas não-nulas da matriz;
-
•
é um arranjo cujos elementos são a posição no arranjo em que cada coluna da matriz começa a ser representada. O número de elementos de -ésima coluna da matriz dado por .
O método scipy.sparse.csc_array permite a alocação de matrizes no formato CSC.
Exemplo 1.1.5.
No Exemplo 1.1.3, alocamos a matriz
| (1.43) |
no formato COO. Aqui, vamos converter a alocação para o formato CSC e, então, verificar seus atributos.
d = [2. 3. -1. 1. 2. -2. -1. 1.] l = [0 1 2 0 1 2 1 3] p = [0 1 3 6 8]
Assim sendo, o elemento p[j=2] = 3 aponta para o l[k=3] = 0, o que informa que A[i=0,j=2]=d[k]=1.. Verifique!
Vantagens do formato CSC
-
•
fatiamento por colunas eficiente;
-
•
operações aritméticas eficientes;
-
•
multiplicação matriz vetor eficiente66endnote: 6CSR é mais eficiente em muitos casos..
Desvantagens do formato CSC
-
•
fatiamento por linhas não eficiente;
-
•
custo elevado de realocamento com alteração da esparsidade da matriz.
Observação 1.1.2.
Além dos formatos COO, CSR e CSC, exitem ainda vários outros que podem empregados e que são mais eficientes em determinadas aplicações. Recomendamos a leitura de [9, Seção 3.4] e da documentação do scipy.sparse.
Exercícios
Em revisão
E. 1.1.1.
Considere o problema de Poisson dado no Exemplo 1.1.2.
-
a)
Armazene a matriz do problema discreto associado usando o formato COO.
-
b)
Converta a matriz armazenada para o formato CSR77endnote: 7Use o método coo_matrix.tocsr().. Então, compute a solução do problema discreto com o método spsolve88endnote: 8scipy.sparse.linalg.spsolve é uma implementação do Método LU otimizado para matrizes esparsas..
-
c)
Converta a matriz armazenada para o formato CSC99endnote: 9Use o método coo_matrix.tocsc().. Então, compute a solução do problema discreto com o método spsolve.
-
d)
Compare a eficiência da computação entre os itens b) e c) para tamanhos de malha .
E. 1.1.2.
Considere o seguinte sistema linear
| (1.44) | |||
| (1.45) | |||
| (1.46) |
-
a)
Compute sua solução usando o Algoritmo de Thomas para .
-
b)
Compare a solução obtida no item anterior com a gerada pela função scipy.linalg.solve.
-
c)
Compare a solução com a obtida no item anterior com a gerada pela função scipy.linalg.solve_banded.
- d)
E. 1.1.3.
Considere que o problema de valor de contorno (PVC)
| (1.47) | |||
| (1.48) | |||
| (1.49) |
seja simulado com o Método das Diferenças Finitas1010endnote: 10Consulte mais em Notas de Aula: Matemática Numérica.. Vamos assumir uma discretização espacial uniforme com nodos e tamanho de malha
| (1.50) |
Com isso, temos os nodos , . Nos nodos internos, aplicamos a fórmula de diferenças central
| (1.51) |
onde, . Com isso, a discretização da EDO fornece
| (1.52) |
para . Das condições de contorno temos . Logo, o problema discreto lê-se: encontrar tal que
| (1.53) | |||
| (1.54) | |||
| (1.55) |
-
a)
Calcule a solução analítica do PVC.
-
b)
Use a função scipy.linalg.solve_banded para computar a solução do problema discreto associado para diferentes tamanhos de malha . Compute o erro da solução discreta em relação à solução analítica.
-
c)
Compare a demanda de tempo computacional se a função scipy.linalg.solve for empregada na computação da solução discreta.
E. 1.1.4.
Consideremos o problema trabalho no Exemplo 1.1.2.
-
a)
Use a função scipy.linalg.solve para computar a solução do problema discreto associado para diferentes tamanhos de malha . Compute o erro da solução discreta em relação à solução analítica. Compare as aproximações com a solução analítica
(1.56) -
b)
Compare a demanda de tempo e memória computacional se a função scipy.linalg.solve_banded for empregada na computação da solução discreta.
-
c)
Baseado no Algoritmo de Thomas, implemente o Método de Eliminação Gaussiana otimizado para a matriz banda deste problema. Compare com as abordagens dos itens a) e b).
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.
Matemática Numérica III
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
1.1 Matrizes Esparsas
Em revisão
Uma matriz é dita ser esparsa quando ela tem apenas poucos elementos não nulos. A ideia é que os elementos não nulos não precisam ser guardados na memória do computador, gerando um grande benefício na redução da demanda de armazenamento de dados. O desafio está no desenvolvimento de estruturas de dados para a alocação eficiente de tais matrizes, i.e. que sejam suficientemente adequadas para os métodos numéricos conhecidos.


Matrizes esparsas podem ser classificadas como estruturadas ou não-estruturadas. Uma matriz estruturada é aquela em que as entradas não-nulas formam um padrão regular. Por exemplo, estão dispostas em poucas diagonais ou formam blocos (submatrizes densas) ao longo de sua diagonal principal. No caso de não haver um padrão regular das entradas não-nulas, a matriz esparsa é dita ser não-estruturada. Consulte a Figura 1.1 para exemplos.
A esparsidade de uma matriz é a porcentagem de elementos nulos que ela tem, i.e. para uma matriz quadrada tem-se que a esparsidade é
| (1.1) |
Por exemplo, a matriz identidade de tamanho tem esparsidade
| (1.2) |
1.1.1 Sistemas Tridiagonais
Em revisão
Um sistema tridiagonal tem a seguinte forma matricial
| (1.3) |
Ou seja, é um sistema cuja a matriz dos coeficientes é tridiagonal.
Uma matriz tridiagonal é uma matriz esparsa estruturada. Mais especificamente, é um caso particular de uma matriz banda, em que os elementos não nulos estão dispostos apenas em algumas de suas diagonais. Para armazenarmos tal matriz precisamos alocar apenas os seguintes três vetores
| (1.4) | |||
| (1.5) | |||
| (1.6) |
Ou seja, precisamos armazenar pontos flutuantes em vez de , como seria o caso se a matriz dos coeficientes fosse densa. Com isso, podemos alocar a matriz do sistema da seguinte forma
| (1.7) |
Ou seja, , sendo
| (1.8) |
Exemplo 1.1.1.
Seja o seguinte sistema linear
| (1.9) | |||
| (1.10) | |||
| (1.11) |
O seguinte código Python faz a alocação de seu vetor dos termos constantes e de sua matriz de coeficientes no formato compacto de .
Algoritmo de Thomas (TDMA)
Em revisão
O algoritmo de Thomas11endnote: 1Llewellyn Hilleth Thomas, 1903 - 1992, físico e matemático aplicado britânico. Fonte: Wikipedia. ou TDMA (do inglês, Tridiagonal Matrix Algorithm) é uma forma otimizada do método de eliminação gaussiana22endnote: 2Johann Carl Friedrich Gauss, 1777 - 1855, matemático alemão. Fonte: Wikipédia: Carl Friedrich Gauss. aplicada a sistemas tridiagonais. Enquanto este requer operações, esse demanda apenas .
Eliminando os termos abaixo da diagonal em (1.3), obtemos o sistema equivalente
| (1.12) |
Este é obtido pela seguinte iteração
| (1.13) | |||
| (1.14) | |||
| (1.15) |
onde, o ~ foi esquecido de propósito, indicando a reutilização da matriz e do vetor . A solução do sistema é, então, obtida de baixo para cima, i.e.
| (1.16) | |||
| (1.17) |
com .
1.1.2 Matrizes Banda
Em revisão
Uma matriz banda é aquela em que os elementos não nulos estão dispostos em apenas algumas de suas diagonais. Consulte a Figura 1.2.

Exemplo 1.1.2.
Consideramos o seguinte problema de Poisson33endnote: 3Siméon Denis Poisson, 1781 - 1840, matemático francês. Fonte: Wikipédia:Siméon Denis Poisson.
| (1.18) | |||
| (1.19) | |||
| (1.20) | |||
| (1.21) | |||
| (1.22) |
onde, é o operador laplaciano44endnote: 4Pierre-Simon Laplace, 1749 - 1827, matemático francês. Fonte: Wikipédia: Pierre-Simon Laplace.. Para fixarmos as ideias, vamos assumir
| (1.23) |
Vamos empregar o método de diferenças finitas para computar uma aproximação para a sua solução. Começamos assumindo uma malha uniforme de nodos
| (1.24) | |||
| (1.25) |
com tamanho de malha , e . Empregando a fórmula de diferenças central, encontramos o seguinte problema discreto associado
| (1.26) | |||
| (1.27) | |||
| (1.28) |
Este é um sistema linear . Tomando em conta as condições de contorno, ele pode ser reduzido a um sistema
| (1.29) |
usando a enumeração das incógnitas
| (1.30) |
i.e.
| (1.31) |
para . Consulte a Figura 1.3 para uma representação da enumeração em relação a malha.

Afim de obtermos uma matriz diagonal dominante, vamos ordenar as equações do sistema discreto como segue
-
•
, :
(1.32) -
•
, :
(1.33) -
•
, :
(1.34) -
•
, :
(1.35) -
•
, :
(1.36) -
•
, :
(1.37) -
•
, :
(1.38) -
•
, :
(1.39) -
•
, :
(1.40)
Com isso, temos um sistema com matriz com 5 bandas, consulte a Figura 1.4.

1.1.3 Esquemas de Armazenamento
Em revisão
A ideia é armazenar apenas os elementos não-nulos de uma matriz esparsa, de forma a economizar a demanda de armazenamento computacional. Cuidados devem ser tomados para que a estrutura de armazenamento utilizada seja adequada para a computação das operações matriciais mais comuns.
Formato COO
Em revisão
O formato COO (do inglês, COOrdinate format) é o esquema de armazenamento simples de matrizes esparsas. As estrutura de dados consiste em três arranjos:
-
1.
um arranjo contendo as entradas não-nulas da matriz;
-
2.
um arranjo contendo seus índices de linha;
-
3.
um arranjo contendo seus índices de coluna.
O método scipy.sparse.coo_array permite a alocação de matrizes no formato COO.
Exemplo 1.1.3.
O seguinte código armazena a matriz
| (1.41) |
no formato COO.
Vantagens do formato COO
-
•
Permite a entrada de dados duplicados (simplicidade).
-
•
Conversão rápida para os formatos CSR e CSC55endnote: 5CSR e CSC são formatos de matrizes esparsas mais eficientes para a computação matricial..
Desavantagens do formato COO
-
•
complexidade em operações aritméticas.
-
•
complexidade na extração de submatrizes.
Observação 1.1.1.
(Entradas Duplicadas.) O formato COO permite a entrada duplicada de elementos da matriz. Na conversão para outros formatos (por exemplo, CSR ou CSC), as entradas duplicadas são somadas.
Formato CSR
Em revisão
O formato CSR (do inglês, Compressed Sparse Row) é uma variação do COO que busca diminuir a alocação de dados repetidos. Assim como o COO, o formato conta com três arranjos , , :
-
•
é o arranjo contendo os elementos não-nulos da matriz, ordenados por linhas (i.e., da esquerda para direita, de cima para baixo);
-
•
é o arranjo contendo o índice das colunas das entradas não-nulas da matriz (como no formato COO);
-
•
é um arranjo cujos elementos são a posição no arranjo em que cada linha da matriz começa a ser representada. O número de elementos de -ésima linha da matriz dado por .
O método scipy.sparse.csr_array permite a alocação de matrizes no formato CSR.
Exemplo 1.1.4.
No Exemplo 1.1.3, alocamos a matriz
| (1.42) |
no formato COO. Aqui, vamos converter a alocação para o formato CSR e, então, verificar seus atributos.
d = [ 2. 1. 3. 2. -1. -1. -2. 1.] c = [0 2 1 2 3 1 2 3] p = [0 2 5 7 8]
Por exemplo, o elemento p[i=2] = 5 aponta para o c[k=5] = 1, o que fornece A[i=2,j=1] = d[k] = -1.. Verifique!
Vantagens do formato CSR
-
•
operações aritméticas eficientes;
-
•
fatiamento por linhas eficiente;
-
•
multiplicação matriz vetor eficiente.
Desvantagens do formato CSR
-
•
fatiamento por colunas não eficiente;
-
•
custo elevado de realocamento com alteração da esparsidade da matriz.
Formato CSC
Em revisão
O formato CSC (do inglês, Compressed Sparse Column) é uma variação análoga do CSR, mas para armazenamento por colunas. O formato conta com três arranjos , , :
-
•
é o arranjo contendo os elementos não-nulos da matriz, ordenados por colunas (i.e., de cima para baixo, da esquerda para direita);
-
•
é o arranjo contendo o índice das linhas das entradas não-nulas da matriz;
-
•
é um arranjo cujos elementos são a posição no arranjo em que cada coluna da matriz começa a ser representada. O número de elementos de -ésima coluna da matriz dado por .
O método scipy.sparse.csc_array permite a alocação de matrizes no formato CSC.
Exemplo 1.1.5.
No Exemplo 1.1.3, alocamos a matriz
| (1.43) |
no formato COO. Aqui, vamos converter a alocação para o formato CSC e, então, verificar seus atributos.
d = [2. 3. -1. 1. 2. -2. -1. 1.] l = [0 1 2 0 1 2 1 3] p = [0 1 3 6 8]
Assim sendo, o elemento p[j=2] = 3 aponta para o l[k=3] = 0, o que informa que A[i=0,j=2]=d[k]=1.. Verifique!
Vantagens do formato CSC
-
•
fatiamento por colunas eficiente;
-
•
operações aritméticas eficientes;
-
•
multiplicação matriz vetor eficiente66endnote: 6CSR é mais eficiente em muitos casos..
Desvantagens do formato CSC
-
•
fatiamento por linhas não eficiente;
-
•
custo elevado de realocamento com alteração da esparsidade da matriz.
Observação 1.1.2.
Além dos formatos COO, CSR e CSC, exitem ainda vários outros que podem empregados e que são mais eficientes em determinadas aplicações. Recomendamos a leitura de [9, Seção 3.4] e da documentação do scipy.sparse.
Exercícios
Em revisão
E. 1.1.1.
Considere o problema de Poisson dado no Exemplo 1.1.2.
-
a)
Armazene a matriz do problema discreto associado usando o formato COO.
-
b)
Converta a matriz armazenada para o formato CSR77endnote: 7Use o método coo_matrix.tocsr().. Então, compute a solução do problema discreto com o método spsolve88endnote: 8scipy.sparse.linalg.spsolve é uma implementação do Método LU otimizado para matrizes esparsas..
-
c)
Converta a matriz armazenada para o formato CSC99endnote: 9Use o método coo_matrix.tocsc().. Então, compute a solução do problema discreto com o método spsolve.
-
d)
Compare a eficiência da computação entre os itens b) e c) para tamanhos de malha .
E. 1.1.2.
Considere o seguinte sistema linear
| (1.44) | |||
| (1.45) | |||
| (1.46) |
-
a)
Compute sua solução usando o Algoritmo de Thomas para .
-
b)
Compare a solução obtida no item anterior com a gerada pela função scipy.linalg.solve.
-
c)
Compare a solução com a obtida no item anterior com a gerada pela função scipy.linalg.solve_banded.
- d)
E. 1.1.3.
Considere que o problema de valor de contorno (PVC)
| (1.47) | |||
| (1.48) | |||
| (1.49) |
seja simulado com o Método das Diferenças Finitas1010endnote: 10Consulte mais em Notas de Aula: Matemática Numérica.. Vamos assumir uma discretização espacial uniforme com nodos e tamanho de malha
| (1.50) |
Com isso, temos os nodos , . Nos nodos internos, aplicamos a fórmula de diferenças central
| (1.51) |
onde, . Com isso, a discretização da EDO fornece
| (1.52) |
para . Das condições de contorno temos . Logo, o problema discreto lê-se: encontrar tal que
| (1.53) | |||
| (1.54) | |||
| (1.55) |
-
a)
Calcule a solução analítica do PVC.
-
b)
Use a função scipy.linalg.solve_banded para computar a solução do problema discreto associado para diferentes tamanhos de malha . Compute o erro da solução discreta em relação à solução analítica.
-
c)
Compare a demanda de tempo computacional se a função scipy.linalg.solve for empregada na computação da solução discreta.
E. 1.1.4.
Consideremos o problema trabalho no Exemplo 1.1.2.
-
a)
Use a função scipy.linalg.solve para computar a solução do problema discreto associado para diferentes tamanhos de malha . Compute o erro da solução discreta em relação à solução analítica. Compare as aproximações com a solução analítica
(1.56) -
b)
Compare a demanda de tempo e memória computacional se a função scipy.linalg.solve_banded for empregada na computação da solução discreta.
-
c)
Baseado no Algoritmo de Thomas, implemente o Método de Eliminação Gaussiana otimizado para a matriz banda deste problema. Compare com as abordagens dos itens a) e b).
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.