Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Matemática Numérica I
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
2.3 Iteração de Ponto Fixo
Um ponto fixo de uma função é um ponto tal que
| (2.47) |
Geometricamente, pontos fixos são interseções do gráfico da com a reta , veja a Figura 2.4.
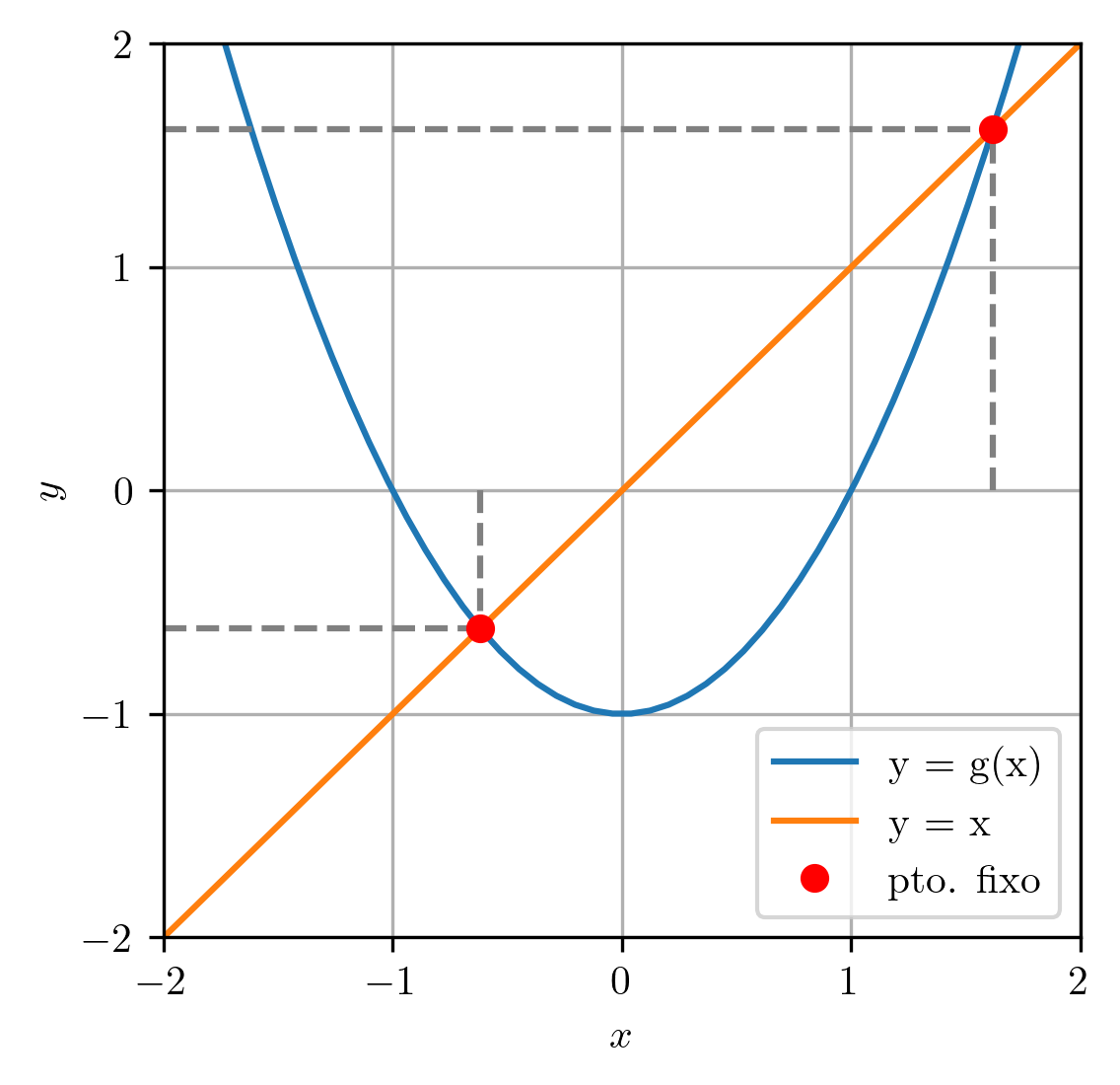
Observamos que toda equação de uma incógnita pode ser reescrita de forma equivalente como um problema de ponto fixo.
Exemplo 2.3.1.
Consideremos o problema de resolver
| (2.48) | ||||
Podemos reescrevê-la como o problema de se obter os zeros da seguinte função
| (2.49) | ||||
Por sua vez, este problema é equivalente aos seguintes problemas de ponto fixo (entre outros):
-
a)
(2.50) -
b)
(2.51)
Na Figura 2.5 podemos observar que os zeros da (a saber, e ) coincidem com os pontos fixos das funções e .
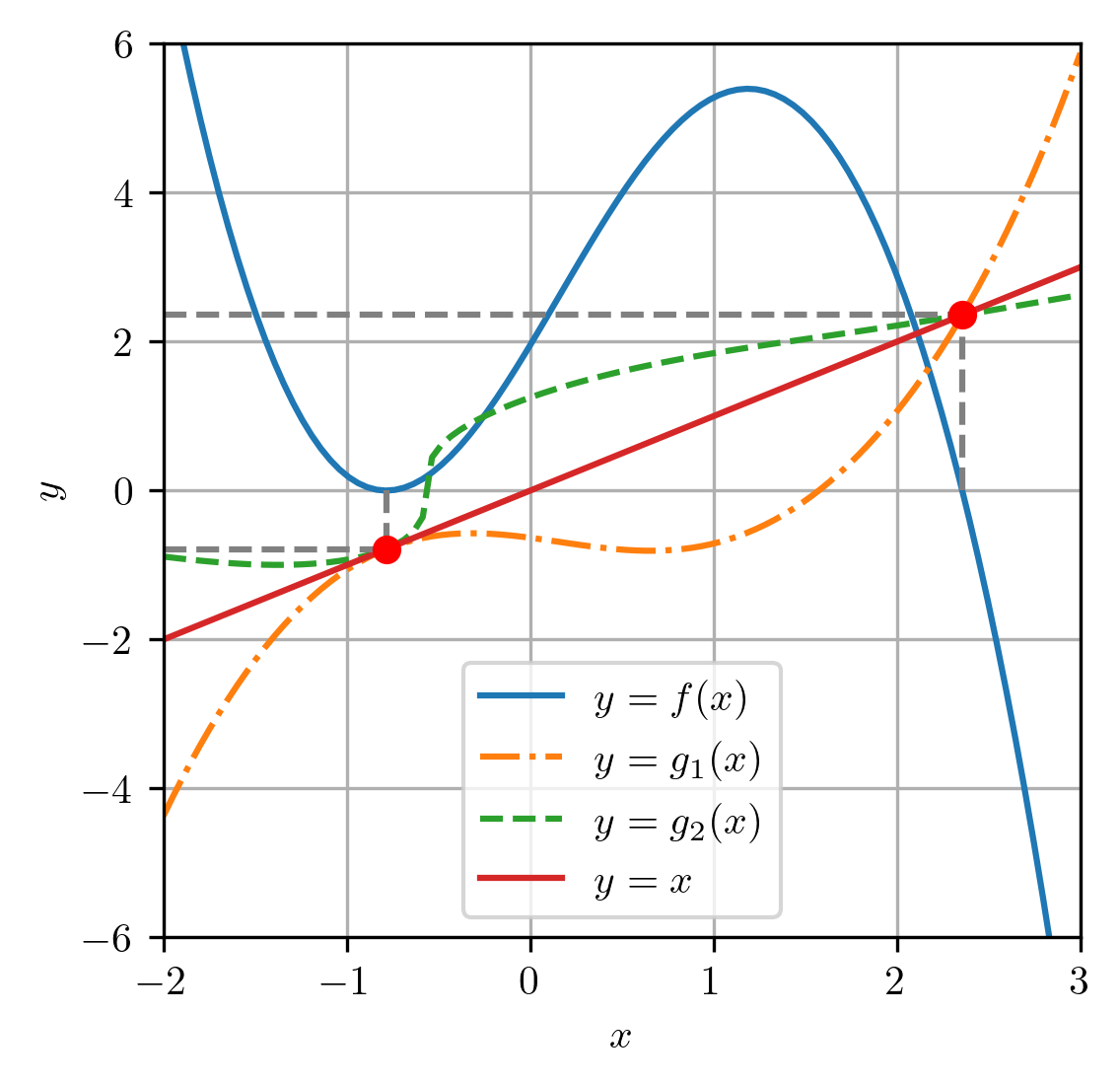
Em muitos casos, é possível obter aproximações de um ponto fixo de uma dada função pela chamada iteração de ponto fixo:
| (2.52) | ||||
| (2.53) |
com .
Exemplo 2.3.2.
Vamos estudar as seguintes iterações de ponto fixo com as funções e consideradas no Exemplo 2.3.1.
-
a)
Função com .
(2.54) (2.55) (2.56) (2.57) (2.58) (2.59) (2.60) (2.61) (2.62) (2.63) (2.64) Neste caso as iterações de ponto fixo convergem (lentamente) para o ponto fixo .
-
b)
Função com .
Este valor inicial está próximo do ponto fixo , entretanto as iterações de ponto fixo divergem:
(2.65) (2.66) (2.67) (2.68) (2.69) -
c)
Função com . Neste caso, as iterações de ponto fixo convergem (rapidamente) para o ponto fixo próximo:
(2.70) (2.71) (2.72) (2.73) (2.74) (2.75)
Este último exemplo mostra que a iteração do ponto fixo nem sempre é convergente. Antes de vermos condições suficientes para a convergência, vejamos sua interpretação geométrica.
2.3.1 Interpretação Geométrica
A Figura 2.6 apresenta o caso de uma iteração de ponto fixo convergente. As iterações iniciam-se no ponto e seguem para e .
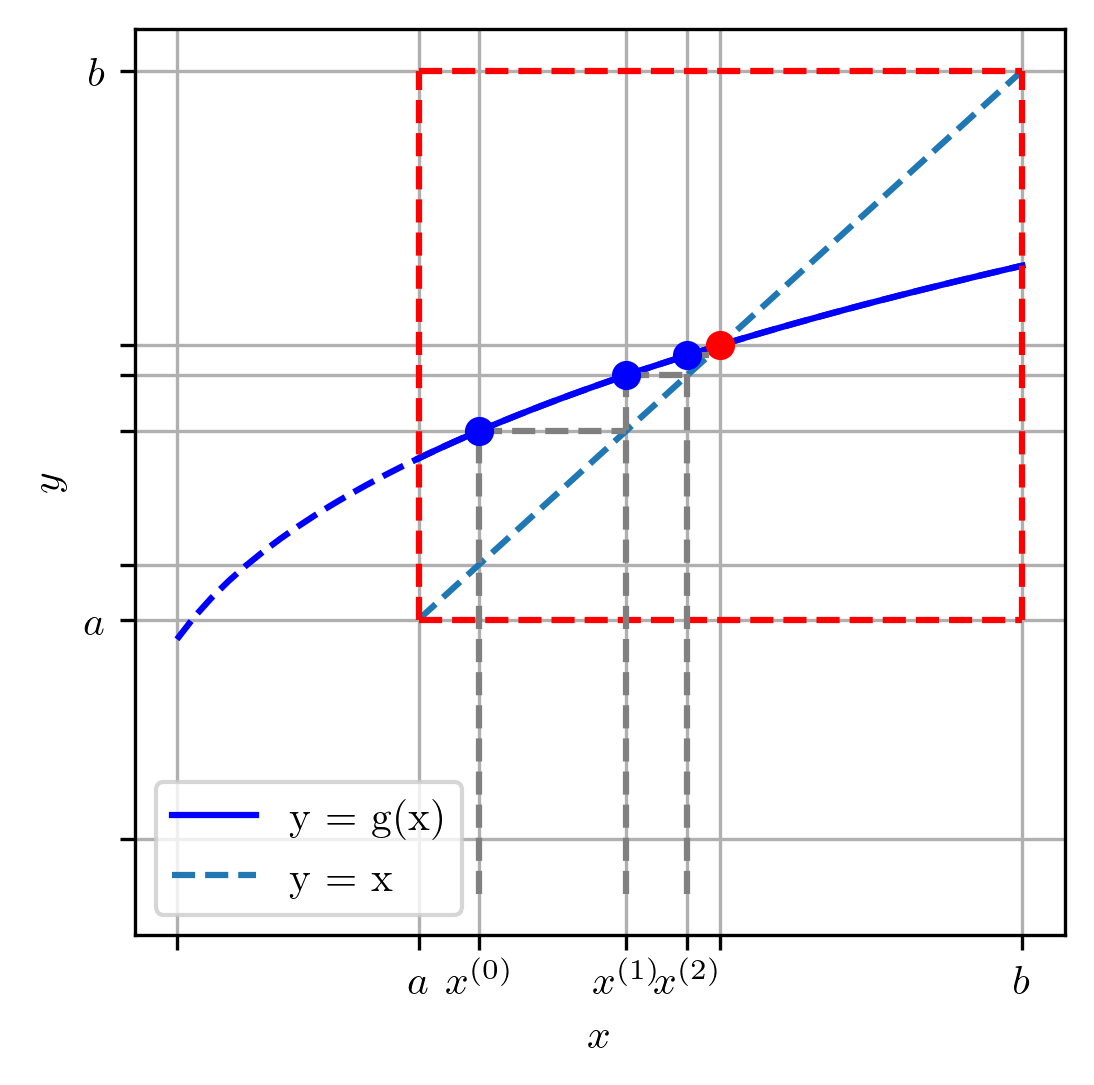
2.3.2 Análise Numérica
O seguinte teorema nos fornece condições suficientes para a convergência das iterações de ponto fixo.
Teorema 2.3.1.
(Teorema do Ponto Fixo.) Seja função continuamente diferenciável satisfazendo ambas as seguintes condições
-
a)
,
-
b)
para todo .
Então, tem um único ponto fixo e as iterações
| (2.76) |
convergem para , para qualquer escolha de .
Demonstração.
Da hipótese b), temos que é uma contração com
| (2.77) |
para quaisquer . Com isso, da hipótese a) e tomando , temos
| (2.78) | ||||
| (2.79) | ||||
| (2.80) |
para . Como , temos quando e, portanto, converge para algum .
De fato, é ponto fixo de , pois da continuidade da , temos
| (2.81) | ||||
| (2.82) |
Por fim, é único, pois assumindo a existência de outro ponto fixo teríamos
| (2.83) | ||||
| (2.84) | ||||
| (2.85) |
∎
Observação 2.3.1.
(Ordem de Convergência.) A iteração de ponto fixo tem ordem de convergência linear
| (2.86) |
onde é a constante dada na hipótese do Teorema do Ponto Fixo. Além disso, isso mostra que quanto menor o valor da constante , mais rápida é a convergência das iterações de ponto fixo.
2.3.3 Zero de Funções
Dado um problema de encontrar um zero de uma função (i.e., resolver ), podemos construir uma função com ponto fixo no zero de e aplicarmos a iteração de ponto fixo para computá-lo. Para tanto, observamos que
| (2.87) | |||
| (2.88) | |||
| (2.89) |
com escolhido de forma a satisfazer as hipóteses do Teorema do Ponto Fixo (Teorema 2.3.1).
Exemplo 2.3.3.
Retornamos ao problema de encontrar o zero da função
| (2.90) | ||||
no intervalo . Para construir uma função para a iteração de ponto fixo neste intervalo, podemos tomar
| (2.91) |
com . A Figura 2.7 mostra esboços dos gráficos de e no intervalos e podemos observar que esta escolha de faz com que a satisfaça o Teorema do Ponto Fixo.
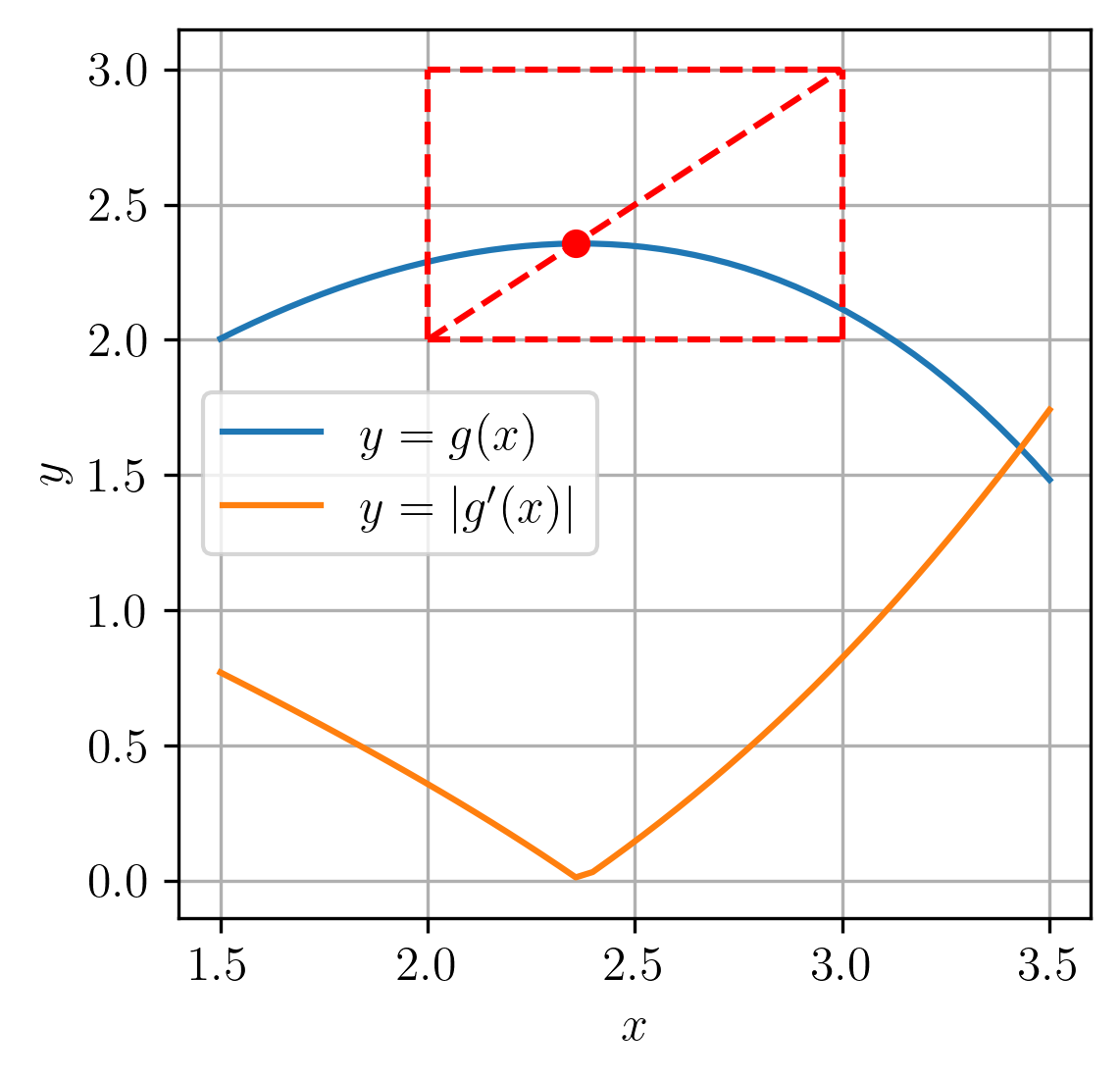
Então, fazendo as iterações de ponto fixo com aproximação inicial , obtemos os resultados apresentados na Tabela 2.3.
| 0 | -x- | |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
2.3.4 Exercícios
E. 2.3.1.
Forneça o(s) ponto(s) fixo(s) de
| (2.92) |
Resposta 0.
E. 2.3.2.
Verifique se a iteração de ponto fixo é convergente para as seguintes funções e aproximações iniciais:
-
a)
,
-
b)
,
Justifique sua resposta.
Resposta 0.
a) Convergente; b) Divergente.
E. 2.3.3.
Considere o problema de computar uma aproximação do zero de . Resolva-o aplicando a iteração de ponto fixo para a função auxiliar
| (2.93) |
restrita ao intervalo com aproximação inicial . Escolha o melhor valor de entre os seguintes:
-
1.
-
2.
-
3.
-
4.
Então, compute uma aproximação do zero de com dígitos significativos de precisão.
Resposta 0.
;
E. 2.3.4.
Seja
| (2.94) | ||||
-
a)
Aplique a iteração de ponto fixo na função auxiliar
(2.95) para algum adequado, de forma que aproximação inicial leve a iterações de ponto fixo que convirjam para , zero de multiplicidade par de .
-
b)
Mostre que para qualquer valor de . Por que isso explica a lenta convergência observada no item a)?
-
c)
Alternativamente, verifique que a abordagem da iteração de ponto fixo converge muito mais rápido para se aplicada à derivada de , i.e. aplicando a iteração à função auxiliar
(2.96) para um valor de adequado.
Resposta 0.
a) ; b) Pois, não há que satisfaz o Teorema do Ponto Fixo.; c)
E. 2.3.5.
Use o Método da Iteração de Ponto Fixo para aproximar um zero de
| (2.97) |
no intervalo inicial .
E. 2.3.6.
Use o Método da Iteração de Ponto Fixo para computar a(s) solução(ões) das seguintes equações com precisão de 8 dígitos significativos.
-
a)
para .
-
b)
para .
Resposta 0.
a) ; b) ;
E. 2.3.7.
Use o Método de Iteração de Ponto Fixo para encontrar uma aproximação com precisão de dígitos significativos do zero de
| (2.98) | ||||
no intervalo .
Resposta 0.
E. 2.3.8.
Use o Método de Iteração de Ponto Fixo para encontrar uma aproximação com precisão de do zero de
| (2.99) | ||||
no intervalo . Forneça a aproximação computada com dígitos significativos por arredondamento.
Resposta 0.
E. 2.3.9.
Use o Método da Iteração de Ponto Fixo para encontrar o ponto crítico1717endnote: 17Definimos que é ponto crítico de uma dada , quando ou . de
| (2.100) |
no intervalo . Obtenha o resultado com precisão de dígitos significativos por arredondamento.
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.
Matemática Numérica I
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
2.3 Iteração de Ponto Fixo
Um ponto fixo de uma função é um ponto tal que
| (2.47) |
Geometricamente, pontos fixos são interseções do gráfico da com a reta , veja a Figura 2.4.

Observamos que toda equação de uma incógnita pode ser reescrita de forma equivalente como um problema de ponto fixo.
Exemplo 2.3.1.
Consideremos o problema de resolver
| (2.48) | ||||
Podemos reescrevê-la como o problema de se obter os zeros da seguinte função
| (2.49) | ||||
Por sua vez, este problema é equivalente aos seguintes problemas de ponto fixo (entre outros):
-
a)
(2.50) -
b)
(2.51)
Na Figura 2.5 podemos observar que os zeros da (a saber, e ) coincidem com os pontos fixos das funções e .

Em muitos casos, é possível obter aproximações de um ponto fixo de uma dada função pela chamada iteração de ponto fixo:
| (2.52) | ||||
| (2.53) |
com .
Exemplo 2.3.2.
Vamos estudar as seguintes iterações de ponto fixo com as funções e consideradas no Exemplo 2.3.1.
-
a)
Função com .
(2.54) (2.55) (2.56) (2.57) (2.58) (2.59) (2.60) (2.61) (2.62) (2.63) (2.64) Neste caso as iterações de ponto fixo convergem (lentamente) para o ponto fixo .
-
b)
Função com .
Este valor inicial está próximo do ponto fixo , entretanto as iterações de ponto fixo divergem:
(2.65) (2.66) (2.67) (2.68) (2.69) -
c)
Função com . Neste caso, as iterações de ponto fixo convergem (rapidamente) para o ponto fixo próximo:
(2.70) (2.71) (2.72) (2.73) (2.74) (2.75)
Este último exemplo mostra que a iteração do ponto fixo nem sempre é convergente. Antes de vermos condições suficientes para a convergência, vejamos sua interpretação geométrica.
2.3.1 Interpretação Geométrica
A Figura 2.6 apresenta o caso de uma iteração de ponto fixo convergente. As iterações iniciam-se no ponto e seguem para e .

2.3.2 Análise Numérica
O seguinte teorema nos fornece condições suficientes para a convergência das iterações de ponto fixo.
Teorema 2.3.1.
(Teorema do Ponto Fixo.) Seja função continuamente diferenciável satisfazendo ambas as seguintes condições
-
a)
,
-
b)
para todo .
Então, tem um único ponto fixo e as iterações
| (2.76) |
convergem para , para qualquer escolha de .
Demonstração.
Da hipótese b), temos que é uma contração com
| (2.77) |
para quaisquer . Com isso, da hipótese a) e tomando , temos
| (2.78) | ||||
| (2.79) | ||||
| (2.80) |
para . Como , temos quando e, portanto, converge para algum .
De fato, é ponto fixo de , pois da continuidade da , temos
| (2.81) | ||||
| (2.82) |
Por fim, é único, pois assumindo a existência de outro ponto fixo teríamos
| (2.83) | ||||
| (2.84) | ||||
| (2.85) |
∎
Observação 2.3.1.
(Ordem de Convergência.) A iteração de ponto fixo tem ordem de convergência linear
| (2.86) |
onde é a constante dada na hipótese do Teorema do Ponto Fixo. Além disso, isso mostra que quanto menor o valor da constante , mais rápida é a convergência das iterações de ponto fixo.
2.3.3 Zero de Funções
Dado um problema de encontrar um zero de uma função (i.e., resolver ), podemos construir uma função com ponto fixo no zero de e aplicarmos a iteração de ponto fixo para computá-lo. Para tanto, observamos que
| (2.87) | |||
| (2.88) | |||
| (2.89) |
com escolhido de forma a satisfazer as hipóteses do Teorema do Ponto Fixo (Teorema 2.3.1).
Exemplo 2.3.3.
Retornamos ao problema de encontrar o zero da função
| (2.90) | ||||
no intervalo . Para construir uma função para a iteração de ponto fixo neste intervalo, podemos tomar
| (2.91) |
com . A Figura 2.7 mostra esboços dos gráficos de e no intervalos e podemos observar que esta escolha de faz com que a satisfaça o Teorema do Ponto Fixo.

Então, fazendo as iterações de ponto fixo com aproximação inicial , obtemos os resultados apresentados na Tabela 2.3.
| 0 | -x- | |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
2.3.4 Exercícios
E. 2.3.1.
Forneça o(s) ponto(s) fixo(s) de
| (2.92) |
Resposta 0.
E. 2.3.2.
Verifique se a iteração de ponto fixo é convergente para as seguintes funções e aproximações iniciais:
-
a)
,
-
b)
,
Justifique sua resposta.
Resposta 0.
a) Convergente; b) Divergente.
E. 2.3.3.
Considere o problema de computar uma aproximação do zero de . Resolva-o aplicando a iteração de ponto fixo para a função auxiliar
| (2.93) |
restrita ao intervalo com aproximação inicial . Escolha o melhor valor de entre os seguintes:
-
1.
-
2.
-
3.
-
4.
Então, compute uma aproximação do zero de com dígitos significativos de precisão.
Resposta 0.
;
E. 2.3.4.
Seja
| (2.94) | ||||
-
a)
Aplique a iteração de ponto fixo na função auxiliar
(2.95) para algum adequado, de forma que aproximação inicial leve a iterações de ponto fixo que convirjam para , zero de multiplicidade par de .
-
b)
Mostre que para qualquer valor de . Por que isso explica a lenta convergência observada no item a)?
-
c)
Alternativamente, verifique que a abordagem da iteração de ponto fixo converge muito mais rápido para se aplicada à derivada de , i.e. aplicando a iteração à função auxiliar
(2.96) para um valor de adequado.
Resposta 0.
a) ; b) Pois, não há que satisfaz o Teorema do Ponto Fixo.; c)
E. 2.3.5.
Use o Método da Iteração de Ponto Fixo para aproximar um zero de
| (2.97) |
no intervalo inicial .
E. 2.3.6.
Use o Método da Iteração de Ponto Fixo para computar a(s) solução(ões) das seguintes equações com precisão de 8 dígitos significativos.
-
a)
para .
-
b)
para .
Resposta 0.
a) ; b) ;
E. 2.3.7.
Use o Método de Iteração de Ponto Fixo para encontrar uma aproximação com precisão de dígitos significativos do zero de
| (2.98) | ||||
no intervalo .
Resposta 0.
E. 2.3.8.
Use o Método de Iteração de Ponto Fixo para encontrar uma aproximação com precisão de do zero de
| (2.99) | ||||
no intervalo . Forneça a aproximação computada com dígitos significativos por arredondamento.
Resposta 0.
E. 2.3.9.
Use o Método da Iteração de Ponto Fixo para encontrar o ponto crítico1717endnote: 17Definimos que é ponto crítico de uma dada , quando ou . de
| (2.100) |
no intervalo . Obtenha o resultado com precisão de dígitos significativos por arredondamento.
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.