Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Equações Diferenciais Ordinárias
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
2.2 Equação separável
Uma EDO de primeira ordem
| (2.124) |
é dita ser uma equação separável quando pode ser reescrita na seguinte forma
| (2.125) |
Exemplo 2.2.1.
Vejamos os seguintes casos.
-
a)
É separável a EDO
(2.126) pois pode ser reescrita como segue
(2.127) (2.128) (2.129) - b)
Agora, vamos ver como podemos resolver uma EDO separável. Consideremos a equação separável
| (2.131) |
Sejam, também, e primitivas de e , respectivamente. I.e.
| (2.132) | |||
| (2.133) |
Lembrando que , temos da regra da cadeia que
| (2.134) | ||||
| (2.135) |
Ou seja, a EDO (2.131) pode ser reescrita na forma
| (2.136) |
ou ainda,
| (2.137) |
Então, integrando em relação a , obtemos
| (2.138) |
a qual é uma equação algébrica para que, com sorte, pode ser usada para explicitar a solução da EDO (2.131).
Exemplo 2.2.2.
Vamos resolver a seguinte EDO separável:
| (2.139) |
-
a)
Método 1. Primeiramente, reescrevemos a EDO no formato (2.125):
(2.140) Então, calculamos as primitivas
(2.141) (2.142) (2.143) e
(2.144) (2.145) (2.146) Então, segue que a EDO resume-se a seguinte equação algébrica
(2.147) (2.148) a qual é uma equação implícita da solução geral .
-
b)
Método 2. A EDO separável
(2.149) pode ser reescrita como
(2.150) Integrando ambos os lados desta equação, obtemos
(2.151) a qual é equivalente a solução obtida em (2.148).
Na figura abaixo, temos esboços dos gráficos da solução para diferentes valores de .
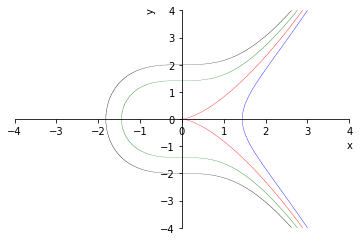
No Python, podemos computar a solução com os seguintes comandos:
Os esboços dos gráficos podem ser feitos com:
Observação 2.2.1.
Como vimos no exemplo anterior (Exemplo 2.2.2), a solução geral de uma EDO separável nem sempre pode ser explicitada. Em muitos casos o procedimento de separar as variáveis nos leva a obter a solução da EDO na forma de uma equação algébrica implícita.
2.2.1 Equação de Verhulst
A equação de Verhulst33endnote: 3Pierre François Verhulst, 1804-1849, matemático belga. (ou equação logística) é um clássico modelo de crescimento populacional. Trata-se da seguinte equação autônoma
| (2.152) |
onde é a medida de tamanho da população e os parâmetros são: a taxa de crescimento intrínseca e o nível de saturação.
Antes de resolvermos esta equação, vamos fazer algumas observações que podem ser obtidas diretamente da EDO. Do cálculo, temos que se para todos os valores de , então é constante, i.e. a população se mantém constante. A derivada é nula quando o lado direito de (2.152) for nulo, i.e.
| (2.153) |
Isso ocorre quando ou quando . Ou seja, se a população é nula não há crescimento populacional, bem como, não há crescimento se a população estiver em seu nível de saturação.
Agora, o que ocorre se a população for ? Neste caso, temos
| (2.154) |
ou seja, a população cresce. Por outro lado, se (a população está acima de seu nível de saturação), então
| (2.155) |
a população decresce. Estas conclusões também nos levam a inferir que
| (2.156) |
para qualquer população inicial não nula.
Solução da equação logística
Consideramos o seguinte PVI
| (2.157) | |||
| (2.158) |
A equação de Verhulst é uma EDO separável, daí segue que
| (2.159) | |||
| (2.160) |
Vamos integrar o lado esquerdo desta última equação44endnote: 4Vamos usar de decomposição em frações parciais.
| (2.161) | ||||
| (2.162) |
Logo, a solução da equação logística satisfaz a seguinte equação algébrica
| (2.163) |
onde é uma constante a determinar. Antes, observamos que esta equação é equivalente a
| (2.164) |
Aplicando a função exponencial, obtemos
| (2.165) |
Da condição inicial , encontramos
| (2.166) |
Agora, podemos isolar em (2.165) como segue:
| (2.167) | |||
| (2.168) | |||
| (2.169) | |||
| (2.170) |
Então, multiplicando em cima e em baixo por , obtemos
| (2.171) |
Por fim, de (2.166), obtemos a solução
| (2.172) |
Da solução, corroboramos que a população permanece constante quando ou . Ainda, se ou , temos que
| (2.173) | ||||
| (2.174) |
Exemplo 2.2.3.
Vamos usar a equação de Verhulst para modelar a dinâmica de uma população com taxa de crescimento intrínseca e nível de saturação (bilhão). Pelo que vimos nesta subsecção, temos o modelo
| (2.175) | |||
| (2.176) |
onde é a solução no tempo e é a população inicial.
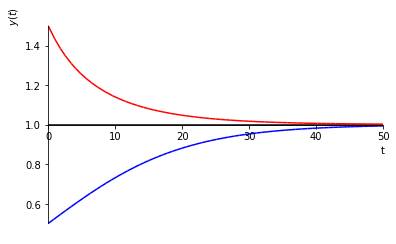
Exercícios resolvidos
Solução 0.
Separando as variáveis, obtemos
| (2.179) | |||
| (2.180) | |||
| (2.181) |
Integrando, obtemos a solução geral
| (2.182) |
ER 2.2.2.
Calcule a solução do PVI
| (2.183) | |||
| (2.184) |
Solução 0.
Separamos as variáveis e integramos
| (2.185) | |||
| (2.186) | |||
| (2.187) | |||
| (2.188) |
Determinamos a constante pela aplicação da condição inicial . Ou seja, temos
| (2.189) | |||
| (2.190) |
Logo, a solução do PVI é dada pela equação algébrica
| (2.191) |
Buscando explicitar a solução, observamos que
| (2.192) | |||
| (2.193) |
Lembrando que , temos necessariamente que
| (2.194) |
ER 2.2.3.
(Crescimento populacional com limiar) Considere o seguinte modelo de crescimento populacional
onde é o tamanho da população, é a população inicial e são parâmetros . Forneça os valores de para os quais a população é crescente.
Solução 0.
A população é crescente quando
| (2.195) |
Logo, precisamos ter
| (2.196) |
Isto ocorre quando
| (2.197) | |||
| (2.198) |
Logo, concluímos que uma população inicial é necessária para produzir uma taxa de crescimento populacional positiva.
Exercícios
E. 2.2.1.
Calcule a solução de
| (2.199) | |||
| (2.200) |
Resposta 0.
.
E. 2.2.2.
Resolva a EDO
| (2.201) |
Resposta 0.
E. 2.2.3.
Resolva o PVI
| (2.202) |
Resposta 0.
E. 2.2.4.
Considere o seguinte modelo de crescimento populacional
onde é o tamanho da população, é a população inicial e são parâmetros . Qual é a tendência da população quando e
-
a)
;
-
b)
;
-
c)
;
-
d)
Resposta 0.
a) ; b) ; c) ; d) .
E. 2.2.5.
Resolva o seguinte modelo de crescimento populacional
onde é o tamanho da população, é a população inicial e são parâmetros .
Resposta 0.
.
E. 2.2.6.
Considere o seguinte modelo de crescimento populacional
onde é o tamanho da população, é a população inicial e são parâmetros , . Qual é a tendência da população quando e
-
a)
;
-
b)
;
-
c)
-
d)
;
-
e)
-
f)
Resposta 0.
a) ; b) ; c) ; d) ; e) ; f) .
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.
Equações Diferenciais Ordinárias
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
2.2 Equação separável
Uma EDO de primeira ordem
| (2.124) |
é dita ser uma equação separável quando pode ser reescrita na seguinte forma
| (2.125) |
Exemplo 2.2.1.
Vejamos os seguintes casos.
-
a)
É separável a EDO
(2.126) pois pode ser reescrita como segue
(2.127) (2.128) (2.129) - b)
Agora, vamos ver como podemos resolver uma EDO separável. Consideremos a equação separável
| (2.131) |
Sejam, também, e primitivas de e , respectivamente. I.e.
| (2.132) | |||
| (2.133) |
Lembrando que , temos da regra da cadeia que
| (2.134) | ||||
| (2.135) |
Ou seja, a EDO (2.131) pode ser reescrita na forma
| (2.136) |
ou ainda,
| (2.137) |
Então, integrando em relação a , obtemos
| (2.138) |
a qual é uma equação algébrica para que, com sorte, pode ser usada para explicitar a solução da EDO (2.131).
Exemplo 2.2.2.
Vamos resolver a seguinte EDO separável:
| (2.139) |
-
a)
Método 1. Primeiramente, reescrevemos a EDO no formato (2.125):
(2.140) Então, calculamos as primitivas
(2.141) (2.142) (2.143) e
(2.144) (2.145) (2.146) Então, segue que a EDO resume-se a seguinte equação algébrica
(2.147) (2.148) a qual é uma equação implícita da solução geral .
-
b)
Método 2. A EDO separável
(2.149) pode ser reescrita como
(2.150) Integrando ambos os lados desta equação, obtemos
(2.151) a qual é equivalente a solução obtida em (2.148).
Na figura abaixo, temos esboços dos gráficos da solução para diferentes valores de .

No Python, podemos computar a solução com os seguintes comandos:
Os esboços dos gráficos podem ser feitos com:
Observação 2.2.1.
Como vimos no exemplo anterior (Exemplo 2.2.2), a solução geral de uma EDO separável nem sempre pode ser explicitada. Em muitos casos o procedimento de separar as variáveis nos leva a obter a solução da EDO na forma de uma equação algébrica implícita.
2.2.1 Equação de Verhulst
A equação de Verhulst33endnote: 3Pierre François Verhulst, 1804-1849, matemático belga. (ou equação logística) é um clássico modelo de crescimento populacional. Trata-se da seguinte equação autônoma
| (2.152) |
onde é a medida de tamanho da população e os parâmetros são: a taxa de crescimento intrínseca e o nível de saturação.
Antes de resolvermos esta equação, vamos fazer algumas observações que podem ser obtidas diretamente da EDO. Do cálculo, temos que se para todos os valores de , então é constante, i.e. a população se mantém constante. A derivada é nula quando o lado direito de (2.152) for nulo, i.e.
| (2.153) |
Isso ocorre quando ou quando . Ou seja, se a população é nula não há crescimento populacional, bem como, não há crescimento se a população estiver em seu nível de saturação.
Agora, o que ocorre se a população for ? Neste caso, temos
| (2.154) |
ou seja, a população cresce. Por outro lado, se (a população está acima de seu nível de saturação), então
| (2.155) |
a população decresce. Estas conclusões também nos levam a inferir que
| (2.156) |
para qualquer população inicial não nula.
Solução da equação logística
Consideramos o seguinte PVI
| (2.157) | |||
| (2.158) |
A equação de Verhulst é uma EDO separável, daí segue que
| (2.159) | |||
| (2.160) |
Vamos integrar o lado esquerdo desta última equação44endnote: 4Vamos usar de decomposição em frações parciais.
| (2.161) | ||||
| (2.162) |
Logo, a solução da equação logística satisfaz a seguinte equação algébrica
| (2.163) |
onde é uma constante a determinar. Antes, observamos que esta equação é equivalente a
| (2.164) |
Aplicando a função exponencial, obtemos
| (2.165) |
Da condição inicial , encontramos
| (2.166) |
Agora, podemos isolar em (2.165) como segue:
| (2.167) | |||
| (2.168) | |||
| (2.169) | |||
| (2.170) |
Então, multiplicando em cima e em baixo por , obtemos
| (2.171) |
Por fim, de (2.166), obtemos a solução
| (2.172) |
Da solução, corroboramos que a população permanece constante quando ou . Ainda, se ou , temos que
| (2.173) | ||||
| (2.174) |
Exemplo 2.2.3.
Vamos usar a equação de Verhulst para modelar a dinâmica de uma população com taxa de crescimento intrínseca e nível de saturação (bilhão). Pelo que vimos nesta subsecção, temos o modelo
| (2.175) | |||
| (2.176) |
onde é a solução no tempo e é a população inicial.

Exercícios resolvidos
Solução 0.
Separando as variáveis, obtemos
| (2.179) | |||
| (2.180) | |||
| (2.181) |
Integrando, obtemos a solução geral
| (2.182) |
ER 2.2.2.
Calcule a solução do PVI
| (2.183) | |||
| (2.184) |
Solução 0.
Separamos as variáveis e integramos
| (2.185) | |||
| (2.186) | |||
| (2.187) | |||
| (2.188) |
Determinamos a constante pela aplicação da condição inicial . Ou seja, temos
| (2.189) | |||
| (2.190) |
Logo, a solução do PVI é dada pela equação algébrica
| (2.191) |
Buscando explicitar a solução, observamos que
| (2.192) | |||
| (2.193) |
Lembrando que , temos necessariamente que
| (2.194) |
ER 2.2.3.
(Crescimento populacional com limiar) Considere o seguinte modelo de crescimento populacional
onde é o tamanho da população, é a população inicial e são parâmetros . Forneça os valores de para os quais a população é crescente.
Solução 0.
A população é crescente quando
| (2.195) |
Logo, precisamos ter
| (2.196) |
Isto ocorre quando
| (2.197) | |||
| (2.198) |
Logo, concluímos que uma população inicial é necessária para produzir uma taxa de crescimento populacional positiva.
Exercícios
E. 2.2.1.
Calcule a solução de
| (2.199) | |||
| (2.200) |
Resposta 0.
.
E. 2.2.2.
Resolva a EDO
| (2.201) |
Resposta 0.
E. 2.2.3.
Resolva o PVI
| (2.202) |
Resposta 0.
E. 2.2.4.
Considere o seguinte modelo de crescimento populacional
onde é o tamanho da população, é a população inicial e são parâmetros . Qual é a tendência da população quando e
-
a)
;
-
b)
;
-
c)
;
-
d)
Resposta 0.
a) ; b) ; c) ; d) .
E. 2.2.5.
Resolva o seguinte modelo de crescimento populacional
onde é o tamanho da população, é a população inicial e são parâmetros .
Resposta 0.
.
E. 2.2.6.
Considere o seguinte modelo de crescimento populacional
onde é o tamanho da população, é a população inicial e são parâmetros , . Qual é a tendência da população quando e
-
a)
;
-
b)
;
-
c)
-
d)
;
-
e)
-
f)
Resposta 0.
a) ; b) ; c) ; d) ; e) ; f) .
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.
