Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Equações Diferenciais Ordinárias
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
2.3 Equação exata
Uma EDO
| (2.203) |
é uma equação exata quando
| (2.204) |
Neste caso, pode-se calcular uma função tal que
| (2.205) |
Com isso, e lembrando que , a EDO (2.203) é equivalente a55endnote: 5
| (2.206) | ||||
| (2.207) | ||||
| (2.208) |
Logo, temos a solução geral
| (2.209) |
Exemplo 2.3.1.
Vamos resolver a seguinte EDO
| (2.210) |
Denotamos
| (2.211) | ||||
| (2.212) |
Calculando as derivadas parciais
| (2.213) | |||
| (2.214) |
vemos que (2.210) é uma equação exata. Desta forma, buscamos por uma função tal que
| (2.215) |
-
a)
Método 1. Podemos calcular a partir de
(2.216) Integrando em relação a , obtemos
(2.217) (2.218) (2.219) Para encontrar , usamos
(2.220) No caso, temos
(2.221) donde
(2.222) Integrando em relação a , obtemos
(2.223) (2.224) Concluímos que
(2.225) A solução geral da EDO é dada pela equação implícita
(2.226) -
b)
Método 2. Partimos da equação
(2.227) Integrando em relação a , obtemos
(2.228) (2.229) (2.230) Agora, usando
(2.231) temos
(2.232) (2.233) Integrando em relação a , obtemos
(2.234) (2.235) Ou seja, obtivemos
(2.236) o que nos fornece a solução geral
(2.237)
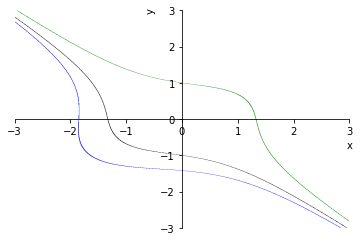
Na figura abaixo, temos esboços da solução geral para diferentes valores de .
No Python, podemos computar a solução geral da EDO com os seguintes códigos:
Os esboços dos gráficos podem ser obtidos com:
2.3.1 Método dos fatores integrantes
Para algumas equações
| (2.238) |
não exatas é possível aplicar o método dos fatores integrantes para convertê-las em equações exatas.
A ideia é buscar por um fator integrante tal que
| (2.239) |
seja uma equação exata, i.e.
| (2.240) |
Ou seja, deve ser tal que
| (2.241) | |||
| (2.242) |
Com isso, pode-se concluir que deve satisfazer
| (2.243) |
Em geral, resolver (2.243) pode ser tão ou mais difícil que resolver a EDO original (2.238). Vejamos alguns casos em que é possível encontrar o fator .
No caso de (função de apenas), a equação (2.243) resume-se a
| (2.244) |
Ou seja, se
| (2.245) |
é função apenas de , então podemos calcular um fator integrante resolvendo a EDO linear (2.244).
Exemplo 2.3.2.
Vamos resolver a EDO
| (2.246) |
Denotando
| (2.247) | ||||
| (2.248) |
vemos que
| (2.249) |
Ou seja, não é uma equação exata. Por outro lado,
| (2.250) | ||||
| (2.251) |
é função apenas de , o que nos indica a existência de um fator integrante satisfazendo a seguinte EDO linear
| (2.252) |
Ou seja, resolvemos
| (2.253) | |||
| (2.254) | |||
| (2.255) | |||
| (2.256) |
Com isso, escolhendo o fator integrante a equação
| (2.257) |
é exata e é equivalente a EDO (2.246). De fato, temos
| (2.258) | ||||
| (2.259) | ||||
| (2.260) | ||||
| (2.261) |
Para resolver (2.257), buscamos por uma função tal que
| (2.262) | |||
| (2.263) | |||
| (2.264) |
Bem como, deve satisfazer
| (2.265) | |||
| (2.266) | |||
| (2.267) | |||
| (2.268) |
Logo, podemos concluir que a solução geral de (2.246) é dada por
| (2.269) |
No Python, podemos computar a solução geral com:
Esta solução é equivalente a (2.269)?
Observação 2.3.1.
A função checkodesol do SymPypermite verificar se uma expressão/equação é solução de uma dada EDO. No caso de exemplo anterior (Exemplo 2.3.2), podemos verificar a solução (2.269) com o seguinte código:
No caso de (função de apenas), a equação (2.243) resume-se a
| (2.270) |
Ou seja, se
| (2.271) |
é função apenas de , então podemos calcular um fator integrante resolvendo a EDO linear (2.270).
Exemplo 2.3.3.
Vamos resolver a EDO
| (2.272) |
Denotando
| (2.273) | ||||
| (2.274) |
vemos que
| (2.275) |
Ou seja, não é uma equação exata. Por outro lado,
| (2.276) |
é função apenas de . Com isso, podemos obter um fator integrante resolvendo a seguinte EDO linear
| (2.277) | |||
| (2.278) | |||
| (2.279) | |||
| (2.280) | |||
| (2.281) |
Desta forma, podemos escolher o fator integrante de forma que a equação
| (2.282) |
é exata e equivalente a EDO (2.272). De fato, temos
| (2.283) | ||||
| (2.284) | ||||
| (2.285) | ||||
| (2.286) |
Sendo (2.282) uma equação exata, buscamos por uma função tal que
| (2.287) | |||
| (2.288) | |||
| (2.289) |
Bem como,
| (2.290) | |||
| (2.291) | |||
| (2.292) | |||
| (2.293) |
Logo, concluímos que a solução geral da EDO (2.272) é
| (2.294) |
Vamos verificar esta solução no Python:
Tendo em vista que o SymPy não resolve esta EDO diretamente, a opção solve_for_func=False foi utilizada para impedir que o SymPy tente resolver a EDO.
Exercícios resolvidos
ER 2.3.1.
Verifique se a EDO
| (2.295) |
é exata. Caso não seja, busque por um fator integrante para reescrevê-la como uma equação exata.
Solução 0.
Para verificarmos se a equação é exata, vamos colocá-la reescrevê-la na seguinte forma
| (2.296) |
Com isso, identificamos
| (2.297) | ||||
| (2.298) |
Ainda, temos
| (2.299) |
e
| (2.300) |
Como
| (2.301) |
concluímos que a EDO é exata.
ER 2.3.2.
Resolva o seguinte PVI:
| (2.302) | |||
| (2.303) |
Solução 0.
Denotando
| (2.304) |
vemos que a EDO associada ao PVI é uma equação exata. Logo, para resolvê-la buscamos por uma função tal que
| (2.305) | |||
| (2.306) | |||
| (2.307) |
Bem como, deve ser tal que
| (2.308) | |||
| (2.309) | |||
| (2.310) | |||
| (2.311) |
Logo, a solução geral da EDO associada é dada por
| (2.312) |
Por fim, aplicando a condição inicial , obtemos
| (2.313) | |||
| (2.314) |
Concluímos que a solução do PVI é dada por
| (2.315) |
Exercícios
E. 2.3.1.
Verifique se a seguinte EDO é exata. Justifique sua resposta.
| (2.316) |
Resposta 0.
Exata
E. 2.3.2.
Resolva a seguinte EDO
| (2.317) |
Resposta 0.
E. 2.3.3.
Mostre que a seguinte EDO não é exata
| (2.318) |
Ainda, mostre que o fator integrante pode ser usado para transformar esta em uma equação exata. Por fim, resolva-a.
Resposta 0.
E. 2.3.4.
Resolva a seguinte EDO
| (2.319) |
Resposta 0.
E. 2.3.5.
Resolva o seguinte PVI
| (2.320) |
Resposta 0.
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.
Equações Diferenciais Ordinárias
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
2.3 Equação exata
Uma EDO
| (2.203) |
é uma equação exata quando
| (2.204) |
Neste caso, pode-se calcular uma função tal que
| (2.205) |
Com isso, e lembrando que , a EDO (2.203) é equivalente a55endnote: 5
| (2.206) | ||||
| (2.207) | ||||
| (2.208) |
Logo, temos a solução geral
| (2.209) |
Exemplo 2.3.1.
Vamos resolver a seguinte EDO
| (2.210) |
Denotamos
| (2.211) | ||||
| (2.212) |
Calculando as derivadas parciais
| (2.213) | |||
| (2.214) |
vemos que (2.210) é uma equação exata. Desta forma, buscamos por uma função tal que
| (2.215) |
-
a)
Método 1. Podemos calcular a partir de
(2.216) Integrando em relação a , obtemos
(2.217) (2.218) (2.219) Para encontrar , usamos
(2.220) No caso, temos
(2.221) donde
(2.222) Integrando em relação a , obtemos
(2.223) (2.224) Concluímos que
(2.225) A solução geral da EDO é dada pela equação implícita
(2.226) -
b)
Método 2. Partimos da equação
(2.227) Integrando em relação a , obtemos
(2.228) (2.229) (2.230) Agora, usando
(2.231) temos
(2.232) (2.233) Integrando em relação a , obtemos
(2.234) (2.235) Ou seja, obtivemos
(2.236) o que nos fornece a solução geral
(2.237)
Na figura abaixo, temos esboços da solução geral para diferentes valores de .

No Python, podemos computar a solução geral da EDO com os seguintes códigos:
Os esboços dos gráficos podem ser obtidos com:
2.3.1 Método dos fatores integrantes
Para algumas equações
| (2.238) |
não exatas é possível aplicar o método dos fatores integrantes para convertê-las em equações exatas.
A ideia é buscar por um fator integrante tal que
| (2.239) |
seja uma equação exata, i.e.
| (2.240) |
Ou seja, deve ser tal que
| (2.241) | |||
| (2.242) |
Com isso, pode-se concluir que deve satisfazer
| (2.243) |
Em geral, resolver (2.243) pode ser tão ou mais difícil que resolver a EDO original (2.238). Vejamos alguns casos em que é possível encontrar o fator .
No caso de (função de apenas), a equação (2.243) resume-se a
| (2.244) |
Ou seja, se
| (2.245) |
é função apenas de , então podemos calcular um fator integrante resolvendo a EDO linear (2.244).
Exemplo 2.3.2.
Vamos resolver a EDO
| (2.246) |
Denotando
| (2.247) | ||||
| (2.248) |
vemos que
| (2.249) |
Ou seja, não é uma equação exata. Por outro lado,
| (2.250) | ||||
| (2.251) |
é função apenas de , o que nos indica a existência de um fator integrante satisfazendo a seguinte EDO linear
| (2.252) |
Ou seja, resolvemos
| (2.253) | |||
| (2.254) | |||
| (2.255) | |||
| (2.256) |
Com isso, escolhendo o fator integrante a equação
| (2.257) |
é exata e é equivalente a EDO (2.246). De fato, temos
| (2.258) | ||||
| (2.259) | ||||
| (2.260) | ||||
| (2.261) |
Para resolver (2.257), buscamos por uma função tal que
| (2.262) | |||
| (2.263) | |||
| (2.264) |
Bem como, deve satisfazer
| (2.265) | |||
| (2.266) | |||
| (2.267) | |||
| (2.268) |
Logo, podemos concluir que a solução geral de (2.246) é dada por
| (2.269) |
No Python, podemos computar a solução geral com:
Esta solução é equivalente a (2.269)?
Observação 2.3.1.
A função checkodesol do SymPypermite verificar se uma expressão/equação é solução de uma dada EDO. No caso de exemplo anterior (Exemplo 2.3.2), podemos verificar a solução (2.269) com o seguinte código:
No caso de (função de apenas), a equação (2.243) resume-se a
| (2.270) |
Ou seja, se
| (2.271) |
é função apenas de , então podemos calcular um fator integrante resolvendo a EDO linear (2.270).
Exemplo 2.3.3.
Vamos resolver a EDO
| (2.272) |
Denotando
| (2.273) | ||||
| (2.274) |
vemos que
| (2.275) |
Ou seja, não é uma equação exata. Por outro lado,
| (2.276) |
é função apenas de . Com isso, podemos obter um fator integrante resolvendo a seguinte EDO linear
| (2.277) | |||
| (2.278) | |||
| (2.279) | |||
| (2.280) | |||
| (2.281) |
Desta forma, podemos escolher o fator integrante de forma que a equação
| (2.282) |
é exata e equivalente a EDO (2.272). De fato, temos
| (2.283) | ||||
| (2.284) | ||||
| (2.285) | ||||
| (2.286) |
Sendo (2.282) uma equação exata, buscamos por uma função tal que
| (2.287) | |||
| (2.288) | |||
| (2.289) |
Bem como,
| (2.290) | |||
| (2.291) | |||
| (2.292) | |||
| (2.293) |
Logo, concluímos que a solução geral da EDO (2.272) é
| (2.294) |
Vamos verificar esta solução no Python:
Tendo em vista que o SymPy não resolve esta EDO diretamente, a opção solve_for_func=False foi utilizada para impedir que o SymPy tente resolver a EDO.
Exercícios resolvidos
ER 2.3.1.
Verifique se a EDO
| (2.295) |
é exata. Caso não seja, busque por um fator integrante para reescrevê-la como uma equação exata.
Solução 0.
Para verificarmos se a equação é exata, vamos colocá-la reescrevê-la na seguinte forma
| (2.296) |
Com isso, identificamos
| (2.297) | ||||
| (2.298) |
Ainda, temos
| (2.299) |
e
| (2.300) |
Como
| (2.301) |
concluímos que a EDO é exata.
ER 2.3.2.
Resolva o seguinte PVI:
| (2.302) | |||
| (2.303) |
Solução 0.
Denotando
| (2.304) |
vemos que a EDO associada ao PVI é uma equação exata. Logo, para resolvê-la buscamos por uma função tal que
| (2.305) | |||
| (2.306) | |||
| (2.307) |
Bem como, deve ser tal que
| (2.308) | |||
| (2.309) | |||
| (2.310) | |||
| (2.311) |
Logo, a solução geral da EDO associada é dada por
| (2.312) |
Por fim, aplicando a condição inicial , obtemos
| (2.313) | |||
| (2.314) |
Concluímos que a solução do PVI é dada por
| (2.315) |
Exercícios
E. 2.3.1.
Verifique se a seguinte EDO é exata. Justifique sua resposta.
| (2.316) |
Resposta 0.
Exata
E. 2.3.2.
Resolva a seguinte EDO
| (2.317) |
Resposta 0.
E. 2.3.3.
Mostre que a seguinte EDO não é exata
| (2.318) |
Ainda, mostre que o fator integrante pode ser usado para transformar esta em uma equação exata. Por fim, resolva-a.
Resposta 0.
E. 2.3.4.
Resolva a seguinte EDO
| (2.319) |
Resposta 0.
E. 2.3.5.
Resolva o seguinte PVI
| (2.320) |
Resposta 0.
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.
