Política de uso de dados

Ao navegar por este site, você concorda com a política de uso de dados.

Política de uso de dados

Ao navegar por este site, você concorda com a política de uso de dados.

| | | |

Cálculo I

1 Limites 1.4 Limites no infinito 1.6 Continuidade

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

1.5 Limites infinitos

O limite de uma função nem sempre existe. Entretanto, em muitos destes casos, podemos concluir mais sobre a tendência da função. Por exemplo, dizemos que o limite de uma dada função $f(x)$ é infinito quando $x$ tende a um número $x_{0}$ , se $f(x)$ é arbitrariamente grande para todos os valores de $x$ suficientemente próximos de $x_{0}$ , mas $x\neq x_{0}$ . Neste caso, escrevemos

\lim_{x\to x_{0}}f(x)=\infty.

(1.211)

A Figura 1.15, é uma ilustração de $f(x)\to\infty$ quando $x\to x_{0}$ .

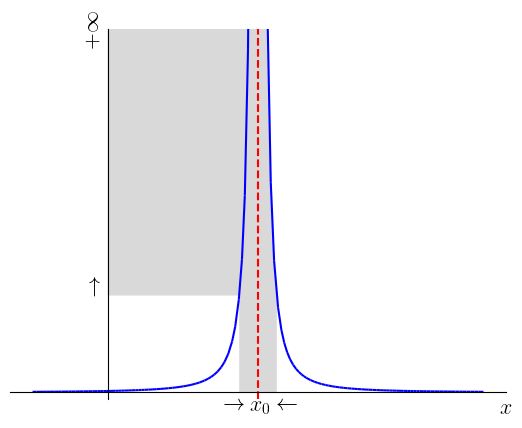
Refer to caption — Figura 1.15: Ilustração de $f(x)\to\infty$ quando $x\to x_{0}$ .

Exemplo 1.5.1.

Vejamos o caso de

\lim_{x\to 0}\frac{1}{x^{2}}.

(1.212)

Ao tomarmos $x$ próximo de $x_{0}=0$ , obtemos os seguintes valores de $f(x)$ :

$x$	$-10^{-1}$	$-10^{-2}$	$-10^{-3}$	$\rightarrow 0\leftarrow$	$10^{-3}$	$10^{-2}$	$10^{-1}$
$f(x)$	$10^{2}$	$10^{4}$	$10^{6}$	$\rightarrow\infty\leftarrow$	$10^{6}$	$10^{4}$	$10^{2}$

Veja o esboço do gráfico de $f(x)$ na Figura 1.16.

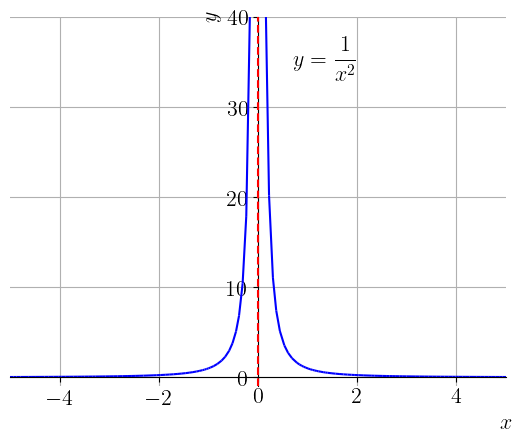
Podemos concluir que os valores de $f(x)$ podem ser tomados arbitrariamente grandes ao escolhermos qualquer $x$ suficientemente próximo de $0$ , com $x\neq 0$ . I.e.,

\lim_{x\to 0}\frac{1}{x^{2}}=\infty.

(1.213)

Com o Python+SymPy, podemos computar este limite com o seguinte comando:

⬇

1 >>> from sympy import *

2 >>> x = Symbol("x")

3 >>> limit(1/x**2, x, 0)

4 oo

Atenção! Na verdade, este comando computa o limite lateral à direita. Na sequência, discutimos sobre limites laterais infinitos.

Definimos os limites laterais infinitos

\lim_{x\to x_{0}^{-}}f(x)=\infty

(1.214)

\lim_{x\to x_{0}^{+}}f(x)=\infty.

(1.215)

No primeiro caso, os valores de $f(x)$ são arbitrariamente grandes conforme os valores de $x\to x_{0}$ e $x<x_{0}$ . No segundo caso, os valores de $f(x)$ são arbitrariamente grandes conforme os valores de $x\to x_{0}$ e $x>x_{0}$ .

Exemplo 1.5.2.

\lim_{x\to 1^{+}}\frac{1}{x-1}=\infty.

(1.216)

De fato, conforme tomamos valores de $x$ próximos de $1$ , com $x>1$ , os valores de $f(x)=1/(x-1)$ tornam-se cada vez maiores. Veja o esboço do gráfico de $f(x)$ na Figura 1.17.

Com o Python+SymPy, podemos computar este limite com o seguinte comando:

⬇

1 >>> from sympy import *

2 >>> x = Symbol("x")

3 >>> limit(1/(x-1), x, 1, '+')

4 oo

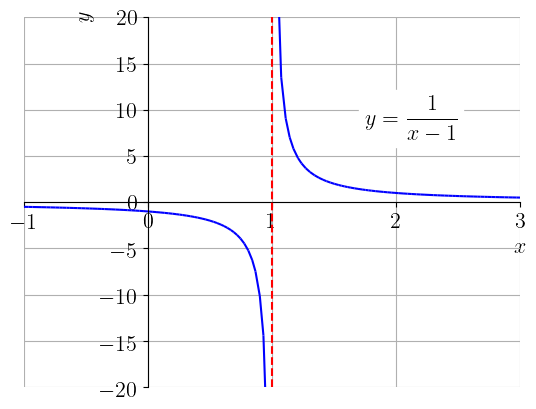
Analogamente a definição de limite infinito, dizemos que o limite de uma dada função $f(x)$ é menos infinito quando $x$ tende a $x_{0}$ , quando $f(x)$ torna-se arbitrariamente pequeno para valores de $x$ suficientemente próximos de $x_{0}$ , com $x\neq x_{0}$ . Neste caso, escrevemos

\lim_{x\to x_{0}}f(x)=-\infty.

(1.217)

De forma similar, definimos os limites laterais $f(x)\to-\infty$ quando $x\to x_{0}^{\pm}$ .

Exemplo 1.5.3.

Observe que

\nexists\lim_{x\to 0}\frac{1}{x}

(1.218)

e que não podemos concluir que este limite é $\infty$ ou $-\infty$ . Isto ocorre, pois

\lim_{x\to 0^{-}}\frac{1}{x}=-\infty

(1.219)

\lim_{x\to 0^{+}}\frac{1}{x}=+\infty.

(1.220)

Exemplo 1.5.4.

\lim_{x\to-1}\frac{-1}{(x+1)^{2}}=-\infty.

(1.221)

De fato, podemos inferir este limite a partir do gráfico da função $f(x)=1/(x+1)^{2}$ . Este é uma translação de uma unidade à esquerda do gráfico de $y=1/x^{2}$ , seguida de uma reflexão em torno de eixo $x$ . Veja a Figura 1.18.

Com o Python+SymPy, podemos computar este limite com o seguinte comando:

⬇

1 >>> from sympy import *

2 >>> x = Symbol("x")

3 >>> limit(-1/(x+1)**2, x, -1)

4 -oo

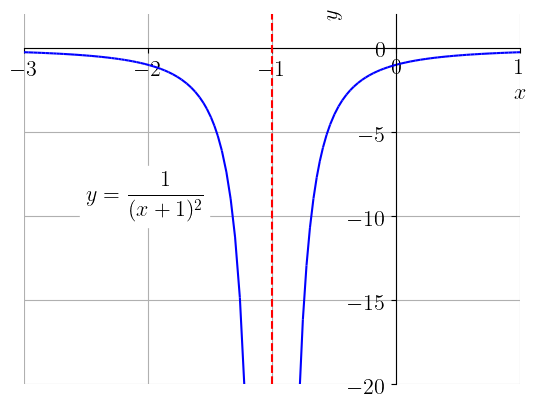
Novamente, observamos que este comando computa apenas o limite lateral à direita.

1.5.1 Assíntotas verticais

Uma reta $x=x_{0}$ é uma assíntota vertical do gráfico de uma função $y=f(x)$ se

\lim_{x\to x_{0}^{-}}f(x)=\pm\infty

(1.222)

\lim_{x\to x_{0}^{+}}f(x)=\pm\infty.

(1.223)

Exemplo 1.5.5.

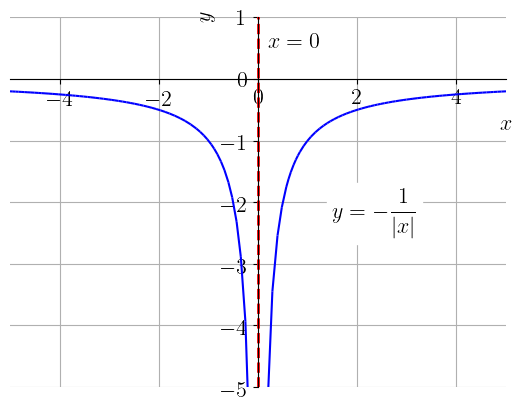
O gráfico da função $f(x)=-1/|x|$ tem uma assíntota vertical em $x=0$ , pois

\lim_{x\to 0}\frac{-1}{|x|}=-\infty.

(1.224)

Veja o esboço de seu gráfico na Figura 1.19.

Exemplo 1.5.6.

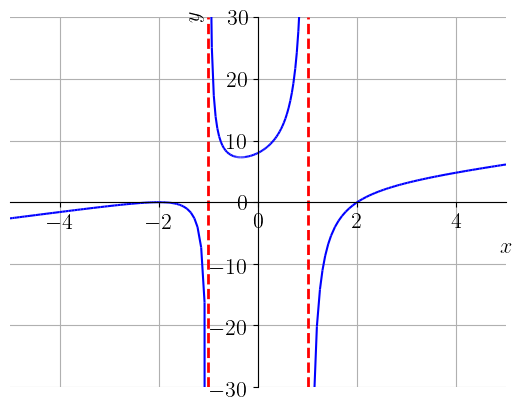
A função $\displaystyle f(x)=\frac{x^{3}+2x^{2}-4x-8}{x^{2}-1}$ não está definida para valores de $x$ tais que seu denominador se anule, i.e.

	$\displaystyle x^{2}-1=0$		(1.225)
	$\displaystyle x_{0}=-1\quad\text{ou}\quad x_{1}=1$		(1.226)

Nestes pontos o gráfico de $f$ pode ter assíntotas verticais. De fato, temos

	$\displaystyle\lim_{x\to-1^{+}}\frac{\cancelto{-3}{x^{3}+2x^{2}-4x-8}}{% \cancelto{0^{-}}{x^{2}-1}}=+\infty,$		(1.227)
	$\displaystyle\lim_{x\to-1^{-}}\frac{\cancelto{-3}{x^{3}+2x^{2}-4x-8}}{% \cancelto{0^{+}}{x^{2}-1}}=-\infty,$		(1.228)

e, também, temos

	$\displaystyle\lim_{x\to 1^{+}}\frac{\cancelto{-9}{x^{3}+2x^{2}-4x-8}}{% \cancelto{0^{+}}{x^{2}-1}}=-\infty,$		(1.229)
	$\displaystyle\lim_{x\to 1^{-}}\frac{\cancelto{-9}{x^{3}+2x^{2}-4x-8}}{% \cancelto{0^{-}}{x^{2}-1}}=+\infty.$		(1.230)

Com isso, temos que as retas $x=-1$ e $x=1$ são assíntotas verticais ao gráfico da função $f$ . Veja a Figura 1.20 para o esboço do gráfico desta função.

Exemplo 1.5.7 (Função logarítmica).

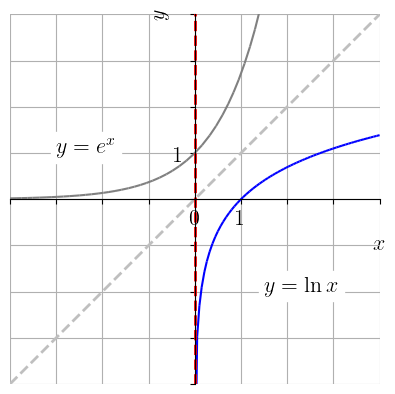
A função logarítmica natural $y=\ln x$ é tal que

\lim_{x\to 0^{+}}\ln x=-\infty

(1.231)

i.e., $x=0$ é uma assíntota vertical ao gráfico de $\ln x$ . Isto decorre do fato de $y=\ln x$ ser a função inversa de $y=e^{x}$ e, esta, ter uma assíntota horizontal $y=0$ ⁴⁴endnote: ⁴Veja o Exemplo 1.4.7.. A Figura 1.21 é um esboço do gráfico da função $\ln x$ .

Exemplo 1.5.8.

As funções trigonométricas $y=\operatorname{tg}x$ e $y=\sec x$ têm assíntotas verticais $x=(2k+1)\frac{\pi}{2}$ para $k$ inteiro. Já, as funções trigonométricas $y=\operatorname{cotg}x$ e $y=\operatorname{cossec}x$ têm assíntotas verticais $x=k\pi$ para $k$ inteiro. Consulte mais em Funções Trigonométricas nas Notas de Aula de Pré-Cálculo.

1.5.2 Assíntotas oblíquas

Além de assíntotas horizontais e verticais, gráficos de funções podem ter assintota oblíquas. Isto ocorre, particularmente, para funções racionais cujo grau do numerador é maior que o do denominador.

Exemplo 1.5.9.

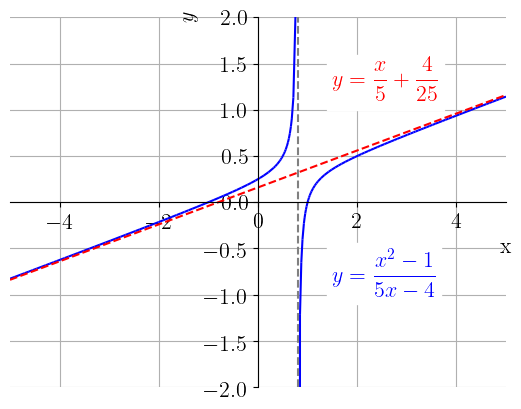
Consideremos a função racional

f(x)=\frac{x^{2}-1}{5x-4}.

(1.232)

Para buscarmos determinar a assíntota oblíqua desta função, dividimos o numerador pelo denominador, de forma a obtermos

f(x)=\underbrace{\left(\frac{x}{5}+\frac{4}{25}\right)}_{\text{quociente}}+% \underbrace{\frac{-\frac{9}{25}}{5x-4}}_{\text{resto}}.

(1.233)

Observamos, agora, que o resto tende a zero quando $x\to\pm\infty$ , i.e. $\displaystyle f(x)\to\frac{x}{5}+\frac{4}{25}$ quando $x\to\pm\infty$ . Com isso, concluímos que $\displaystyle y=\frac{x}{5}+\frac{4}{25}$ é uma assíntota oblíqua ao gráfico de $f(x)$ . Veja a Figura 1.22.

Observação 1.5.1.

Analogamente à assintotas oblíquas, podemos ter outros tipos de assíntotas determinadas por funções de diversos tipos, por exemplo, assíntotas quadráticas.

1.5.3 Limites infinitos no infinito

Escrevemos

\lim_{x\to\infty}f(x)=\infty,

(1.234)

quando os valores da função $f$ são arbitrariamente grandes para todos os valores de $x$ suficientemente grandes. De forma análoga, definimos

\lim_{x\to-\infty}f(x)=\infty,

(1.235)

\lim_{x\to\infty}f(x)=-\infty

(1.236)

\lim_{x\to-\infty}f(x)=-\infty.

(1.237)

Exemplo 1.5.10.

Vejamos os seguintes casos:

a)

$\displaystyle\lim_{x\to\infty}x^{2}=\infty$
b)

$\displaystyle\lim_{x\to-\infty}x^{2}=\infty$
c)

$\displaystyle\lim_{x\to-\infty}x^{3}=-\infty$
d)

$\displaystyle\lim_{x\to\infty}e^{x}=\infty$
e)

$\displaystyle\lim_{x\to\infty}\ln x=\infty$
f)

$\displaystyle\lim_{x\to-\infty}e^{-x}=\infty$

Exemplo 1.5.11.

	$\displaystyle\lim_{x\to\infty}x^{3}-10x^{2}+300=\lim_{x\to\infty}\frac{x^{3}-1% 0x^{2}+300}{1}\cdot\frac{\frac{1}{x^{3}}}{\frac{1}{x^{3}}}$		(1.238)
	$\displaystyle\text{}\quad=\lim_{x\to\infty}\frac{1-\cancelto{0^{+}}{\frac{10}{% x}}+\cancelto{0^{+}}{\frac{300}{x^{3}}}}{\cancelto{0^{+}}{\frac{1}{x^{3}}}}=\infty.$		(1.239)

Proposição 1.5.1.

Dado um polinômio $p(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots+a_{0}$ , temos

\lim_{x\to\pm\infty}p(x)=\lim_{x\to\pm}a_{n}x^{n}.

(1.240)

Exemplo 1.5.12.

Retornando ao exemplo anterior (Exemplo 1.5.11, temos

	$\displaystyle\lim_{x\to\infty}x^{3}-10x^{2}+300=\lim_{x\to\infty}x^{3}$		(1.241)
	$\displaystyle\text{}\quad=\infty.$		(1.242)

1.5.4 Exercícios resolvidos

ER 1.5.1.

Calcule

\lim_{x\to 1^{-}}\frac{x-2}{1-x}.

(1.243)

Solução.

Temos

\lim_{x\to 1^{-}}\frac{\cancelto{-1}{x-2}}{\cancelto{0^{+}}{1-x}}=-\infty.

(1.244)

Outra forma de calcular este limite é observar que $y=1-x\to 0^{+}$ quando $x\to 1^{-}$ . Assim, fazendo a mudança de variável $y=x-1$ , temos

	$\displaystyle\lim_{x\to 1^{-}}\frac{x-2}{1-x}=\lim_{y\to 0^{+}}\frac{y+1-2}{y}$		(1.245)
	$\displaystyle\text{}\quad=\lim_{y\to 0^{+}}\frac{y-1}{y}$		(1.246)
	$\displaystyle\text{}\quad=-\infty.$		(1.247)

Podemos usar o seguinte comandoPython+SymPy para computar este limite:

⬇

1 >>> from sympy import *

2 >>> x = Symbol("x")

3 >>> limit((x-2)/(1-x), x, 1, '-')

4 -oo

ER 1.5.2.

Calcule

\lim_{x\to 1}\ln|x-1|.

(1.248)

Solução.

Começamos observando que

\ln|x-1|=\left\{\begin{array}[]{ll}\ln(1-x)&,x<1,\\ \ln(x-1)&,x>1.\end{array}\right.

(1.249)

Então, calculando o limite lateral à esquerda, temos

	$\displaystyle\lim_{x\to 1^{-}}\ln\|x-1\|=\lim_{x\to 1^{-}}\ln(1-x)$		(1.250)
	$\displaystyle\text{}\quad=\lim_{y\to 0^{+}}\ln y=-\infty.$		(1.251)

Por outro lado, temos

	$\displaystyle\lim_{x\to 1^{+}}\ln\|x-1\|=\lim_{x\to 1^{+}}\ln(x-1)$		(1.252)
	$\displaystyle\text{}\quad=\lim_{y\to 0^{+}}\ln y=-\infty.$		(1.253)

Portanto, concluímos que

\lim_{x\to 1}\ln|x-1|=-\infty.

(1.254)

Podemos usar os seguintes comandos Python+SymPy para computar os limites laterais:

⬇

1 >>> from sympy import *

2 >>> x = Symbol("x")

3 >>> limit(log(abs(x-1)), x, 1, '-')

4 -oo

5 >>> limit(log(abs(x-1)), x, 1, '+')

6 -oo

ER 1.5.3.

Calcule

\lim_{x\to\infty}\frac{x^{3}+2x^{2}-4x-8}{x^{2}-1}.

(1.255)

Solução.

Tratando-se de uma função racional, temos⁷⁷endnote: ⁷Veja a Observação 1.4.1. Veja, também, o gráfico desta função na Figura 1.20.

	$\displaystyle\lim_{x\to\infty}\frac{x^{3}+2x^{2}-4x-8}{x^{2}-1}=\lim_{x\to% \infty}\frac{x^{3}}{x^{2}}$		(1.256)
	$\displaystyle\text{}\quad=\lim_{x\to\infty}x$		(1.257)
	$\displaystyle\text{}\quad=\infty.$		(1.258)

ER 1.5.4.

Calcule

\lim_{x\to\infty}e^{1-x^{2}}.

(1.259)

Solução.

Observamos que $1-x^{2}\to-\infty$ quando $x\to\infty$ . Desta forma, fazendo a mudança de variáveis $y=1-x^{2}$ , temos

\lim_{x\to\infty}e^{1-x^{2}}=\lim_{y\to-\infty}e^{y}=0.

(1.260)

ER 1.5.5.

Calcule

\lim_{x\to\infty}\frac{\sqrt{1+x^{2}}}{2x}.

(1.261)

Solução.

Podemos verificar que trata-se de uma indeterminação do tipo $\infty/\infty$ . Neste caso, podemos calcular o limite pela multiplicação (em cima e em baixo) pelo inverso do fator dominante no radical, i.e. $1/\sqrt{x^{2}}$ . Ou seja, calculamos

	$\displaystyle\lim_{x\to\infty}\frac{\sqrt{1+x^{2}}}{2x}=\lim_{x\to\infty}\frac% {\sqrt{1+x^{2}}}{x}\cdot\frac{\frac{1}{\sqrt{x^{2}}}}{\frac{1}{\sqrt{x^{2}}}}$		(1.262)
	$\displaystyle\text{}\quad=\lim_{x\to\infty}\frac{\sqrt{\frac{1}{x^{2}}+\frac{x% ^{2}}{x^{2}}}}{2\frac{x}{\sqrt{x^{2}}}}.$		(1.263)

Lembramos que $\sqrt{x^{2}}=|x|$ . Como $x\to\infty$ , temos $\sqrt{x^{2}}=|x|=x$ . Logo,

	$\displaystyle\lim_{x\to\infty}\frac{\sqrt{\frac{1}{x^{2}}+\frac{x^{2}}{x^{2}}}% }{2\frac{x}{\sqrt{x^{2}}}}=\lim_{x\to\infty}\frac{\sqrt{\frac{1}{x^{2}}+\frac{% x^{2}}{x^{2}}}}{2\frac{x}{\|x\|}}$		(1.264)
	$\displaystyle\text{}\quad=\lim_{x\to\infty}\frac{\sqrt{\frac{1}{x^{2}}+1}}{2% \frac{x}{x}}$		(1.265)
	$\displaystyle\text{}\quad=\lim_{x\to\infty}\frac{1}{2}\sqrt{\frac{1}{x^{2}}+1}$		(1.266)
	$\displaystyle\text{}\quad=\frac{1}{2}\sqrt{\lim_{x\to\infty}\frac{1}{x^{2}}+1}$		(1.267)
	$\displaystyle\text{}\quad=\frac{1}{2}.$		(1.268)

1.5.5 Exercícios

E. 1.5.1.

Calcule

a)

$\displaystyle\lim_{x\to 0^{+}}x^{-1}$
b)

$\displaystyle\lim_{x\to 0^{-}}-x^{-3}$
c)

$\displaystyle\lim_{x\to 0^{+}}x^{-5}$
d)

$\displaystyle\lim_{x\to 0^{\pm}}x^{-n},\quad n>0\leavevmode\nobreak\ \text{\'{% \i}mpar}$

Resposta.

a) $\infty$ ; b) $\infty$ ; c) $\infty$ ; d) $\pm\infty$

E. 1.5.2.

Calcule

a)

$\displaystyle\lim_{x\to 0^{+}}x^{-2}$
b)

$\displaystyle\lim_{x\to 0^{-}}x^{-4}$
c)

$\displaystyle\lim_{x\to 0^{+}}-x^{-6}$
d)

$\displaystyle\lim_{x\to 0^{\pm}}x^{-n},\quad n>0\leavevmode\nobreak\ \text{\'{% \i}mpar}$

Resposta.

a) $\infty$ ; b) $\infty$ ; c) $-\infty$ ; d) $\infty$

E. 1.5.3.

Calcule

a)

$\displaystyle\lim_{x\to 1^{+}}\frac{1}{x-1}$
b)

$\displaystyle\lim_{x\to 1^{-}}\frac{-2}{x-1}$
c)

$\displaystyle\lim_{x\to-1^{-}}\frac{-2}{1+x}$
d)

$\displaystyle\lim_{x\to-1}\frac{-2}{(x+1)^{2}}$
e)

$\displaystyle\lim_{x\to-1}\frac{x^{2}-3x+2}{x^{2}+2x+1}$

Resposta.

a) $\infty$ ; b) $\infty$ ; c) $-\infty$ ; d) $-\infty$ ; e) $\infty$

E. 1.5.4.

Determine as assíntotas verticais ao gráfico da função

f(x)=\frac{8}{x^{2}-4}.

(1.269)

Resposta.

$x=2$ ; $x=-2$

E. 1.5.5.

Determine as assíntotas verticais ao gráfico da função

f(x)=\frac{x+1}{x^{2}-1}.

(1.270)

Resposta.

$x=1$

E. 1.5.6.

Calcule

\lim_{x\to-\infty}e^{x^{2}-1}.

(1.271)

Resposta.

$\infty$

E. 1.5.7.

Calcule

\lim_{x\to-\infty}x^{3}+10x^{2}-300.

(1.272)

Resposta.

$-\infty$

E. 1.5.8.

Mostre que $y=x^{2}$ é assíntota ao gráfico de

f(x)=\frac{x^{3}+1}{x}.

(1.273)

Resposta.

Dica: Observe que $f(x)=x^{2}+\frac{1}{x}$ e analise o limite de $f(x)$ quando $x\to\pm\infty$ .

E. 1.5.9.

(Aplicação) Na física química, a Equação de Arrhenius⁸⁸endnote: ⁸Svante August Arrhenius, 1859-1927, químico sueco. Fonte: Wikipédia. fornece a taxa de reação $k$ (entre espécies químicas) em função da temperatura $T$ [K]

k=Ae^{-\frac{E_{a}}{RT}},

(1.274)

onde $A>0$ é o fator constante pré-exponencial, $E_{a}>0$ é a energia de ativação e $R>0$ é a constante universal dos gases. Para temperatura constante, a equação acima define a função $k=k(E_{a})$ . Qual é a tendência da taxa de reação $k$ quando $T\to 0^{+}$ .

Resposta.

$k\to 0$ quando $T\to 0^{+}$

E. 1.5.10.

(Aplicação.) A função logística tem aplicações em várias áreas do conhecimento como, por exemplo, na inteligência artificial e na modelagem de crescimento populacional⁹⁹endnote: ⁹Consulte mais em Wikipédia: Função Logística.. Ela tem a forma

\varphi(x)=\frac{1}{1+e^{-x}}

(1.275)

Encontre a(s) assíntota(s) horizontal(ais) dessa função logística.

Resposta.

$y=0$ e $y=1$

E. 1.5.11.

(Aplicação.) O fenômeno de desintegração espontânea do núcleo de um átomo com a emissão de algumas radiações é chamado de radioatividade¹⁰¹⁰endnote: ¹⁰Fonte: Wikipédia.. A lei fundamental do decaimento radiativo estabelece que a taxa de decaimento é proporcional ao número de átomos que ainda não decaíram. Isto nos fornece a equação da lei básica da radioatividade

N=N_{0}e^{-\lambda t}

(1.276)

onde, $N=N(t)$ é o número de átomos no tempo $t$ , $N_{0}\geq 0$ é o número de átomos presentes no tempo inicial $t=0$ e $\lambda>0$ é a constante de decaimento. Qual a tendência de $N$ quando $t\to\infty$ .

Resposta.

$N(t)\to 0$ quando $t\to\infty$

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Cálculo I

1 Limites 1.4 Limites no infinito 1.6 Continuidade

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

1.5 Limites infinitos

\lim_{x\to x_{0}}f(x)=\infty.

(1.211)

A Figura 1.15, é uma ilustração de $f(x)\to\infty$ quando $x\to x_{0}$ .

Exemplo 1.5.1.

Vejamos o caso de

\lim_{x\to 0}\frac{1}{x^{2}}.

(1.212)

Ao tomarmos $x$ próximo de $x_{0}=0$ , obtemos os seguintes valores de $f(x)$ :

$x$	$-10^{-1}$	$-10^{-2}$	$-10^{-3}$	$\rightarrow 0\leftarrow$	$10^{-3}$	$10^{-2}$	$10^{-1}$
$f(x)$	$10^{2}$	$10^{4}$	$10^{6}$	$\rightarrow\infty\leftarrow$	$10^{6}$	$10^{4}$	$10^{2}$

Veja o esboço do gráfico de $f(x)$ na Figura 1.16.

Podemos concluir que os valores de $f(x)$ podem ser tomados arbitrariamente grandes ao escolhermos qualquer $x$ suficientemente próximo de $0$ , com $x\neq 0$ . I.e.,

\lim_{x\to 0}\frac{1}{x^{2}}=\infty.

(1.213)

Com o Python+SymPy, podemos computar este limite com o seguinte comando:

⬇

1 >>> from sympy import *

2 >>> x = Symbol("x")

3 >>> limit(1/x**2, x, 0)

4 oo

Atenção! Na verdade, este comando computa o limite lateral à direita. Na sequência, discutimos sobre limites laterais infinitos.

Definimos os limites laterais infinitos

\lim_{x\to x_{0}^{-}}f(x)=\infty

(1.214)

\lim_{x\to x_{0}^{+}}f(x)=\infty.

(1.215)

Exemplo 1.5.2.

\lim_{x\to 1^{+}}\frac{1}{x-1}=\infty.

(1.216)

De fato, conforme tomamos valores de $x$ próximos de $1$ , com $x>1$ , os valores de $f(x)=1/(x-1)$ tornam-se cada vez maiores. Veja o esboço do gráfico de $f(x)$ na Figura 1.17.

Com o Python+SymPy, podemos computar este limite com o seguinte comando:

⬇

1 >>> from sympy import *

2 >>> x = Symbol("x")

3 >>> limit(1/(x-1), x, 1, '+')

4 oo

\lim_{x\to x_{0}}f(x)=-\infty.

(1.217)

De forma similar, definimos os limites laterais $f(x)\to-\infty$ quando $x\to x_{0}^{\pm}$ .

Exemplo 1.5.3.

Observe que

\nexists\lim_{x\to 0}\frac{1}{x}

(1.218)

e que não podemos concluir que este limite é $\infty$ ou $-\infty$ . Isto ocorre, pois

\lim_{x\to 0^{-}}\frac{1}{x}=-\infty

(1.219)

\lim_{x\to 0^{+}}\frac{1}{x}=+\infty.

(1.220)

Exemplo 1.5.4.

\lim_{x\to-1}\frac{-1}{(x+1)^{2}}=-\infty.

(1.221)

Com o Python+SymPy, podemos computar este limite com o seguinte comando:

⬇

1 >>> from sympy import *

2 >>> x = Symbol("x")

3 >>> limit(-1/(x+1)**2, x, -1)

4 -oo

Novamente, observamos que este comando computa apenas o limite lateral à direita.

1.5.1 Assíntotas verticais

Uma reta $x=x_{0}$ é uma assíntota vertical do gráfico de uma função $y=f(x)$ se

\lim_{x\to x_{0}^{-}}f(x)=\pm\infty

(1.222)

\lim_{x\to x_{0}^{+}}f(x)=\pm\infty.

(1.223)

Exemplo 1.5.5.

O gráfico da função $f(x)=-1/|x|$ tem uma assíntota vertical em $x=0$ , pois

\lim_{x\to 0}\frac{-1}{|x|}=-\infty.

(1.224)

Veja o esboço de seu gráfico na Figura 1.19.

Exemplo 1.5.6.

A função $\displaystyle f(x)=\frac{x^{3}+2x^{2}-4x-8}{x^{2}-1}$ não está definida para valores de $x$ tais que seu denominador se anule, i.e.

	$\displaystyle x^{2}-1=0$		(1.225)
	$\displaystyle x_{0}=-1\quad\text{ou}\quad x_{1}=1$		(1.226)

Nestes pontos o gráfico de $f$ pode ter assíntotas verticais. De fato, temos

	$\displaystyle\lim_{x\to-1^{+}}\frac{\cancelto{-3}{x^{3}+2x^{2}-4x-8}}{% \cancelto{0^{-}}{x^{2}-1}}=+\infty,$		(1.227)
	$\displaystyle\lim_{x\to-1^{-}}\frac{\cancelto{-3}{x^{3}+2x^{2}-4x-8}}{% \cancelto{0^{+}}{x^{2}-1}}=-\infty,$		(1.228)

e, também, temos

	$\displaystyle\lim_{x\to 1^{+}}\frac{\cancelto{-9}{x^{3}+2x^{2}-4x-8}}{% \cancelto{0^{+}}{x^{2}-1}}=-\infty,$		(1.229)
	$\displaystyle\lim_{x\to 1^{-}}\frac{\cancelto{-9}{x^{3}+2x^{2}-4x-8}}{% \cancelto{0^{-}}{x^{2}-1}}=+\infty.$		(1.230)

Com isso, temos que as retas $x=-1$ e $x=1$ são assíntotas verticais ao gráfico da função $f$ . Veja a Figura 1.20 para o esboço do gráfico desta função.

Exemplo 1.5.7 (Função logarítmica).

A função logarítmica natural $y=\ln x$ é tal que

\lim_{x\to 0^{+}}\ln x=-\infty

(1.231)

Exemplo 1.5.8.

1.5.2 Assíntotas oblíquas

Exemplo 1.5.9.

Consideremos a função racional

f(x)=\frac{x^{2}-1}{5x-4}.

(1.232)

Para buscarmos determinar a assíntota oblíqua desta função, dividimos o numerador pelo denominador, de forma a obtermos

f(x)=\underbrace{\left(\frac{x}{5}+\frac{4}{25}\right)}_{\text{quociente}}+% \underbrace{\frac{-\frac{9}{25}}{5x-4}}_{\text{resto}}.

(1.233)

Observação 1.5.1.

Analogamente à assintotas oblíquas, podemos ter outros tipos de assíntotas determinadas por funções de diversos tipos, por exemplo, assíntotas quadráticas.

1.5.3 Limites infinitos no infinito

Escrevemos

\lim_{x\to\infty}f(x)=\infty,

(1.234)

quando os valores da função $f$ são arbitrariamente grandes para todos os valores de $x$ suficientemente grandes. De forma análoga, definimos

\lim_{x\to-\infty}f(x)=\infty,

(1.235)

\lim_{x\to\infty}f(x)=-\infty

(1.236)

\lim_{x\to-\infty}f(x)=-\infty.

(1.237)

Exemplo 1.5.10.

Vejamos os seguintes casos:

a)

$\displaystyle\lim_{x\to\infty}x^{2}=\infty$
b)

$\displaystyle\lim_{x\to-\infty}x^{2}=\infty$
c)

$\displaystyle\lim_{x\to-\infty}x^{3}=-\infty$
d)

$\displaystyle\lim_{x\to\infty}e^{x}=\infty$
e)

$\displaystyle\lim_{x\to\infty}\ln x=\infty$
f)

$\displaystyle\lim_{x\to-\infty}e^{-x}=\infty$

Exemplo 1.5.11.

	$\displaystyle\lim_{x\to\infty}x^{3}-10x^{2}+300=\lim_{x\to\infty}\frac{x^{3}-1% 0x^{2}+300}{1}\cdot\frac{\frac{1}{x^{3}}}{\frac{1}{x^{3}}}$		(1.238)
	$\displaystyle\text{}\quad=\lim_{x\to\infty}\frac{1-\cancelto{0^{+}}{\frac{10}{% x}}+\cancelto{0^{+}}{\frac{300}{x^{3}}}}{\cancelto{0^{+}}{\frac{1}{x^{3}}}}=\infty.$		(1.239)

Proposição 1.5.1.

Dado um polinômio $p(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots+a_{0}$ , temos

\lim_{x\to\pm\infty}p(x)=\lim_{x\to\pm}a_{n}x^{n}.

(1.240)

Exemplo 1.5.12.

Retornando ao exemplo anterior (Exemplo 1.5.11, temos

	$\displaystyle\lim_{x\to\infty}x^{3}-10x^{2}+300=\lim_{x\to\infty}x^{3}$		(1.241)
	$\displaystyle\text{}\quad=\infty.$		(1.242)

1.5.4 Exercícios resolvidos

ER 1.5.1.

Calcule

\lim_{x\to 1^{-}}\frac{x-2}{1-x}.

(1.243)

Solução.

Temos

\lim_{x\to 1^{-}}\frac{\cancelto{-1}{x-2}}{\cancelto{0^{+}}{1-x}}=-\infty.

(1.244)

Outra forma de calcular este limite é observar que $y=1-x\to 0^{+}$ quando $x\to 1^{-}$ . Assim, fazendo a mudança de variável $y=x-1$ , temos

	$\displaystyle\lim_{x\to 1^{-}}\frac{x-2}{1-x}=\lim_{y\to 0^{+}}\frac{y+1-2}{y}$		(1.245)
	$\displaystyle\text{}\quad=\lim_{y\to 0^{+}}\frac{y-1}{y}$		(1.246)
	$\displaystyle\text{}\quad=-\infty.$		(1.247)

Podemos usar o seguinte comandoPython+SymPy para computar este limite:

⬇

1 >>> from sympy import *

2 >>> x = Symbol("x")

3 >>> limit((x-2)/(1-x), x, 1, '-')

4 -oo

ER 1.5.2.

Calcule

\lim_{x\to 1}\ln|x-1|.

(1.248)

Solução.

Começamos observando que

\ln|x-1|=\left\{\begin{array}[]{ll}\ln(1-x)&,x<1,\\ \ln(x-1)&,x>1.\end{array}\right.

(1.249)

Então, calculando o limite lateral à esquerda, temos

	$\displaystyle\lim_{x\to 1^{-}}\ln\|x-1\|=\lim_{x\to 1^{-}}\ln(1-x)$		(1.250)
	$\displaystyle\text{}\quad=\lim_{y\to 0^{+}}\ln y=-\infty.$		(1.251)

Por outro lado, temos

	$\displaystyle\lim_{x\to 1^{+}}\ln\|x-1\|=\lim_{x\to 1^{+}}\ln(x-1)$		(1.252)
	$\displaystyle\text{}\quad=\lim_{y\to 0^{+}}\ln y=-\infty.$		(1.253)

Portanto, concluímos que

\lim_{x\to 1}\ln|x-1|=-\infty.

(1.254)

Podemos usar os seguintes comandos Python+SymPy para computar os limites laterais:

⬇

1 >>> from sympy import *

2 >>> x = Symbol("x")

3 >>> limit(log(abs(x-1)), x, 1, '-')

4 -oo

5 >>> limit(log(abs(x-1)), x, 1, '+')

6 -oo

ER 1.5.3.

Calcule

\lim_{x\to\infty}\frac{x^{3}+2x^{2}-4x-8}{x^{2}-1}.

(1.255)

Solução.

Tratando-se de uma função racional, temos⁷⁷endnote: ⁷Veja a Observação 1.4.1. Veja, também, o gráfico desta função na Figura 1.20.

	$\displaystyle\lim_{x\to\infty}\frac{x^{3}+2x^{2}-4x-8}{x^{2}-1}=\lim_{x\to% \infty}\frac{x^{3}}{x^{2}}$		(1.256)
	$\displaystyle\text{}\quad=\lim_{x\to\infty}x$		(1.257)
	$\displaystyle\text{}\quad=\infty.$		(1.258)

ER 1.5.4.

Calcule

\lim_{x\to\infty}e^{1-x^{2}}.

(1.259)

Solução.

Observamos que $1-x^{2}\to-\infty$ quando $x\to\infty$ . Desta forma, fazendo a mudança de variáveis $y=1-x^{2}$ , temos

\lim_{x\to\infty}e^{1-x^{2}}=\lim_{y\to-\infty}e^{y}=0.

(1.260)

ER 1.5.5.

Calcule

\lim_{x\to\infty}\frac{\sqrt{1+x^{2}}}{2x}.

(1.261)

Solução.

	$\displaystyle\lim_{x\to\infty}\frac{\sqrt{1+x^{2}}}{2x}=\lim_{x\to\infty}\frac% {\sqrt{1+x^{2}}}{x}\cdot\frac{\frac{1}{\sqrt{x^{2}}}}{\frac{1}{\sqrt{x^{2}}}}$		(1.262)
	$\displaystyle\text{}\quad=\lim_{x\to\infty}\frac{\sqrt{\frac{1}{x^{2}}+\frac{x% ^{2}}{x^{2}}}}{2\frac{x}{\sqrt{x^{2}}}}.$		(1.263)

Lembramos que $\sqrt{x^{2}}=|x|$ . Como $x\to\infty$ , temos $\sqrt{x^{2}}=|x|=x$ . Logo,

	$\displaystyle\lim_{x\to\infty}\frac{\sqrt{\frac{1}{x^{2}}+\frac{x^{2}}{x^{2}}}% }{2\frac{x}{\sqrt{x^{2}}}}=\lim_{x\to\infty}\frac{\sqrt{\frac{1}{x^{2}}+\frac{% x^{2}}{x^{2}}}}{2\frac{x}{\|x\|}}$		(1.264)
	$\displaystyle\text{}\quad=\lim_{x\to\infty}\frac{\sqrt{\frac{1}{x^{2}}+1}}{2% \frac{x}{x}}$		(1.265)
	$\displaystyle\text{}\quad=\lim_{x\to\infty}\frac{1}{2}\sqrt{\frac{1}{x^{2}}+1}$		(1.266)
	$\displaystyle\text{}\quad=\frac{1}{2}\sqrt{\lim_{x\to\infty}\frac{1}{x^{2}}+1}$		(1.267)
	$\displaystyle\text{}\quad=\frac{1}{2}.$		(1.268)

1.5.5 Exercícios

E. 1.5.1.

Calcule

a)

$\displaystyle\lim_{x\to 0^{+}}x^{-1}$
b)

$\displaystyle\lim_{x\to 0^{-}}-x^{-3}$
c)

$\displaystyle\lim_{x\to 0^{+}}x^{-5}$
d)

$\displaystyle\lim_{x\to 0^{\pm}}x^{-n},\quad n>0\leavevmode\nobreak\ \text{\'{% \i}mpar}$

Resposta.

a) $\infty$ ; b) $\infty$ ; c) $\infty$ ; d) $\pm\infty$

E. 1.5.2.

Calcule

a)

$\displaystyle\lim_{x\to 0^{+}}x^{-2}$
b)

$\displaystyle\lim_{x\to 0^{-}}x^{-4}$
c)

$\displaystyle\lim_{x\to 0^{+}}-x^{-6}$
d)

$\displaystyle\lim_{x\to 0^{\pm}}x^{-n},\quad n>0\leavevmode\nobreak\ \text{\'{% \i}mpar}$

Resposta.

a) $\infty$ ; b) $\infty$ ; c) $-\infty$ ; d) $\infty$

E. 1.5.3.

Calcule

a)

$\displaystyle\lim_{x\to 1^{+}}\frac{1}{x-1}$
b)

$\displaystyle\lim_{x\to 1^{-}}\frac{-2}{x-1}$
c)

$\displaystyle\lim_{x\to-1^{-}}\frac{-2}{1+x}$
d)

$\displaystyle\lim_{x\to-1}\frac{-2}{(x+1)^{2}}$
e)

$\displaystyle\lim_{x\to-1}\frac{x^{2}-3x+2}{x^{2}+2x+1}$

Resposta.

a) $\infty$ ; b) $\infty$ ; c) $-\infty$ ; d) $-\infty$ ; e) $\infty$

E. 1.5.4.

Determine as assíntotas verticais ao gráfico da função

f(x)=\frac{8}{x^{2}-4}.

(1.269)

Resposta.

$x=2$ ; $x=-2$

E. 1.5.5.

Determine as assíntotas verticais ao gráfico da função

f(x)=\frac{x+1}{x^{2}-1}.

(1.270)

Resposta.

$x=1$

E. 1.5.6.

Calcule

\lim_{x\to-\infty}e^{x^{2}-1}.

(1.271)

Resposta.

$\infty$

E. 1.5.7.

Calcule

\lim_{x\to-\infty}x^{3}+10x^{2}-300.

(1.272)

Resposta.

$-\infty$

E. 1.5.8.

Mostre que $y=x^{2}$ é assíntota ao gráfico de

f(x)=\frac{x^{3}+1}{x}.

(1.273)

Resposta.

Dica: Observe que $f(x)=x^{2}+\frac{1}{x}$ e analise o limite de $f(x)$ quando $x\to\pm\infty$ .

E. 1.5.9.

k=Ae^{-\frac{E_{a}}{RT}},

(1.274)

Resposta.

$k\to 0$ quando $T\to 0^{+}$

E. 1.5.10.

\varphi(x)=\frac{1}{1+e^{-x}}

(1.275)

Encontre a(s) assíntota(s) horizontal(ais) dessa função logística.

Resposta.

$y=0$ e $y=1$

E. 1.5.11.

N=N_{0}e^{-\lambda t}

(1.276)

Resposta.

$N(t)\to 0$ quando $t\to\infty$

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Pedro H A Konzen

| | | |