Política de uso de dados

Ao navegar por este site, você concorda com a política de uso de dados.

| | | |

Cálculo I

2 Derivadas 2.4 Derivada de Funções Exponenciais e Logarítmicas 2.6 Derivadas de funções trigonométricas

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

2.5 Regas Básicas de Derivação

2.5.1 Regras da multiplicação por constante e da soma

Sejam $k$ um número real, $u=u(x)$ e $v=v(x)$ funções deriváveis. Temos as seguintes regras básicas de derivação:

•

$\boldsymbol{(k\cdot u)^{\prime}=k\cdot u^{\prime}}$ .

De fato, pela definição da derivada temos

$\displaystyle(k\cdot u)^{\prime}(x)=\lim_{h\to 0}\frac{k\cdot u(x+h)-k\cdot u(%x)}{h}$ (2.239)

$\displaystyle\text{}\quad=\lim_{h\to 0}k\cdot\left(\frac{u(x+h)-u(x)}{h}\right)$ (2.240)

$\displaystyle\text{}\quad=k\cdot\lim_{h\to 0}\cancelto{u^{\prime}}{\frac{u(x+h%)-u(x)}{h}}$ (2.241)

$\displaystyle\text{}\quad=k\cdot u^{\prime}.$ (2.242)

No SymPy, podemos usar os seguintes comandos para obtermos esta regra de derivação:

⬇

1 from sympy import *

2 k = Symbol('k', real=True)

3 u = Function('u', real=True)

4 diff(k*u(x),x)

•

$\boldsymbol{(u\pm v)^{\prime}=u^{\prime}\pm v^{\prime}}$ .

De fato, temos

	$\displaystyle(u+v)^{\prime}(x)=\lim_{h\to 0}\frac{(u+v)(x+h)-(u+v)(x)}{h}$		(2.243)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{u(x+h)+v(x+h)-[u(x)+v(x)]}{h}$		(2.244)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\left[\cancelto{u^{\prime}}{\frac{u(x+h%)-u(x)}{h}}\right.$		(2.245)
	$\displaystyle\text{}\qquad+\left.\cancelto{v^{\prime}}{\frac{v(x+h)-v(x)}{h}}\right]$		(2.246)
	$\displaystyle\text{}\quad=u^{\prime}(x)+v^{\prime}(x).$		(2.247)

Também, como $(-v)^{\prime}=(-1\cdot v)^{\prime}=-1\cdot v^{\prime}=-v^{\prime}$ , temos

(u-v)^{\prime}=[u+(-v)]^{\prime}=u^{\prime}+(-v)^{\prime}=u^{\prime}-v^{\prime}.

(2.248)

No SymPy, podemos usar os seguintes comandos para obtermos a regra de derivação para soma:

⬇

1 from sympy import *

2 u = Function('u', real=True)

3 v = Function('v', real=True)

4 diff(u(x)+v(x),x)

Exemplo 2.5.1.

Vejamos os seguintes casos:

a)

$f(x)=2x$ .

Para calcularmos $f^{\prime}$ , podemos identificar $f=k\cdot u$ , com $k=2$ e $u(x)=x$ . Então, usando a regra da multiplicação por constante $(ku)^{\prime}=ku^{\prime}$ , temos

$f^{\prime}(x)=(2x)^{\prime}=2(x^{\prime})=2\cdot 1=2.$ (2.249)

No SymPy, podemos computar esta derivada com o comando:

⬇

1 from sympy import *

2 x = Symbol('x')

3 diff(2*x,x)
b)

$f(x)=2x+3$ .

Observamos que $f=u+v$ , com $u(x)=2x$ e $v(x)\equiv 3$ . Então, da regra da soma $(u+v)^{\prime}=u^{\prime}+v^{\prime}$ , temos

$f^{\prime}(x)=(2x+3)^{\prime}=(2x)^{\prime}+(3)^{\prime}=2+0=2.$ (2.250)

No SymPy, podemos computar esta derivada com o comando:

⬇

1 from sympy import *

2 x = Symbols('x')

3 diff(2*x+3,x)
c)

$f(x)=e^{x}-x^{2}$ .

Observamos que $f=u-v$ , com $u(x)=e^{x}$ e $v(x)=x^{2}$ . Usando a regra da subtração $(u-v)^{\prime}=u^{\prime}-v^{\prime}$ temos

$f^{\prime}(x)=(e^{x}-x^{2})^{\prime}=(e^{x})^{\prime}-(x^{2})^{\prime}=e^{x}-2x.$ (2.251)

No SymPy, podemos computar esta derivada com o comando:

⬇

1 from sympy import *

2 x = Symbols('x')

3 diff(exp(x)-x**2,x)

2.5.2 Regras do produto e do quociente

Sejam $y=u(x)$ e $y=v(x)$ funções deriváveis. Então:

•

$\boldsymbol{(u\cdot v)^{\prime}=u^{\prime}\cdot v+u\cdot v^{\prime}}$ .

De fato, da definição da derivada temos

	$\displaystyle(uv)^{\prime}(x)=\lim_{h\to 0}\frac{(uv)(x+h)-(uv)(x)}{h}$		(2.252)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{u(x+h)v(x+h)-u(x)v(x)}{h}$		(2.253)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\left[\frac{u(x+h)v(x+h)-u(x)v(x+h)}{h}\right.$		(2.254)
	$\displaystyle\text{}\qquad+\left.\frac{u(x)v(x+h)-u(x)v(x)}{h}\right]$		(2.255)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{u(x+h)-u(x)}{h}v(v+h)$		(2.256)
	$\displaystyle\text{}\qquad+\lim_{h\to 0}u(x)\frac{v(x+h)-v(x)}{h}$		(2.257)
	$\displaystyle\text{}\quad=u^{\prime}(x)v(x)+u(x)v^{\prime}(x).$		(2.258)

No SymPy, podemos usar os seguintes comandos para obtermos tal regra de derivação:

⬇

1 u = Function('u', real=True)

2 v = Function('v', real=True)

3 diff(u(x)*v(x), x)

•

$\displaystyle\boldsymbol{\left(\frac{u}{v}\right)^{\prime}=\frac{u^{\prime}v-%uv^{\prime}}{v^{2}}}$ , no caso de $v(x)\neq 0$ .

De fato, da definição de derivada temos

	$\displaystyle\left(\frac{u}{v}\right)^{\prime}(x)=\lim_{h\to 0}\frac{\left(%\frac{u}{v}\right)(x+h)-\left(\frac{u}{v}\right)(x)}{h}$		(2.259)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{\frac{u(x+h)v(x)-u(x)v(x+h)}{v(x+%h)v(x)}}{h}$		(2.260)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\left[\frac{u(x+h)v(x)-u(x)v(x)}{h}\right.$		(2.261)
	$\displaystyle\text{}\qquad-\left.\frac{u(x)v(x+h)-u(x)v(x)}{h}\right]\frac{1}{%v(x)v(x+h)}$		(2.262)
	$\displaystyle\text{}\quad=\left[\lim_{h\to 0}\cancelto{u^{\prime}(x)v(x)}{%\frac{u(x+h)-u(x)}{h}v(x)}\right.$		(2.263)
	$\displaystyle\text{}\qquad\left.-\lim_{h\to 0}\cancelto{u(x)v^{\prime}(x)}{u(x%)\frac{v(x+h)-v(x)}{h}}\right]\lim_{h\to 0}\cancelto{\frac{1}{v^{2}(x)}}{\frac%{1}{v(x)v(x+h)}}$		(2.264)
	$\displaystyle\text{}\quad=\frac{u^{\prime}(x)v(x)-u(x)v^{\prime}(x)}{v^{2}(x)}.$		(2.265)

No SymPy, podemos usar os seguintes comandos para obtermos tal regra de derivação:

⬇

1 from sympy import *

2 x = Symbol('x')

3 u = Function('u', real=True)

4 v = Function('v', real=True)

5 simplify(diff(u(x)/v(x),x))

Exemplo 2.5.2.

Vamos calcular a derivada em relação a $x$ da função $f(x)=x^{2}(x-1)$ de duas formas.

1.

Por expansão da expressão e utilização da regra da subtração.

$\displaystyle f^{\prime}(x)=[x^{2}(x-1)]^{\prime}$ (2.266)

$\displaystyle\text{}\quad=(x^{3}-x^{2})^{\prime}$ (2.267)

$\displaystyle\text{}\quad=\overbrace{(x^{3})^{\prime}-(x^{2})^{\prime}}^{(u-v)%^{\prime}=u^{\prime}-v^{\prime}}$ (2.268)

$\displaystyle\text{}\quad=3x^{2}-2x,\quad\quad(x^{n})^{\prime}=nx^{n-1}.$ (2.269)
2.

Utilizando a regra do produto.

Observamos que $f=u\cdot v$ , com $u(x)=x^{2}$ e $v(x)=x-1$ . Então, da regra do produto $(uv)^{\prime}=u^{\prime}v+uv^{\prime}$ , com $u^{\prime}(x)=2x$ e $v^{\prime}(x)=1$ , temos

$\displaystyle f^{\prime}(x)=[\overbrace{x^{2}}^{u}\overbrace{(x-1)}^{v}]^{\prime}$ (2.270)

$\displaystyle\text{}\quad=\overbrace{2x\cdot(x-1)}^{u^{\prime}\cdot v}+%\overbrace{x^{2}\cdot 1}^{u\cdot v^{\prime}}$ (2.271)

$\displaystyle\text{}\quad=2x^{2}-2x+x^{2}$ (2.272)

$\displaystyle\text{}\quad=3x^{2}-2x.$ (2.273)

Exemplo 2.5.3.

Vamos calcular a derivada em relação a $x$ de $f(x)=1/x^{2}$ para $x\neq 0$ . Observamos que $f=(u/v)$ com $u(x)\equiv 1$ e $v(x)=x^{2}$ . Tendo em vista que $u^{\prime}(x)\equiv 0$ e $v^{\prime}(x)=2x$ , temos da regra do quociente que

	$\displaystyle f^{\prime}(x)=\left(\frac{1}{x^{2}}\right)^{\prime}$		(2.274)
	$\displaystyle\text{}\quad=\frac{0\cdot x^{2}-1\cdot 2x}{(x^{2})^{2}},\quad%\quad\left[\left(\frac{u}{v}\right)^{\prime}=\frac{u^{\prime}v-uv^{\prime}}{v^%{2}}\right]$		(2.275)
	$\displaystyle\text{}\quad=-\frac{2x}{x^{4}}=-\frac{2}{x^{3}}$		(2.276)
	$\displaystyle\text{}\quad=-2x^{-3}.$		(2.277)

Observação 2.5.1.

Com abuso de linguagem, temos

\boldsymbol{(x^{n})^{\prime}=nx^{n-1}},

(2.278)

com $n$ inteiro. No caso de $n=1$ , temos $(x)^{\prime}\equiv 1$ . No caso de $n<=0$ , devemos ter $x\neq 0$ ¹⁷¹⁷endnote: ¹⁷Devido a indeterminação de $0^{0}$ e a inexistência de $0^{n}$ com $n$ negativo. Mais ainda, a regra também vale para $n=1/2$ , veja o Exemplo 2.2.2.

Exemplo 2.5.4.

Voltando ao exemplo anterior (Exemplo 2.5.3), temos

\left(\frac{1}{x^{2}}\right)^{\prime}=\overbrace{(x^{-2})^{\prime}}^{(x^{n})^{%\prime}}=\overbrace{-2x^{-2-1}}^{nx^{n-1}}=-2x^{-3}.

(2.279)

Exemplo 2.5.5.

Vamos calcular a derivada em relação a $x$ de $f(x)=xe^{x}$ . Usando a regra do produto $(uv)^{\prime}=u^{\prime}v+uv^{\prime}$ com $u(x)=x$ e $v(x)=e^{x}$ , temos

$\displaystyle f^{\prime}(x)$	$\displaystyle=\overbrace{(xe^{x})^{\prime}}^{(uv)^{\prime}}$	(2.280)
	$\displaystyle=\overbrace{1\cdot e^{x}}^{u^{\prime}\cdot v}+\overbrace{x\cdot e%^{x}}^{u\cdot v^{\prime}}$	(2.281)
	$\displaystyle=(x+1)e^{x}.$	(2.282)

2.5.3 Lista de derivadas

	$\displaystyle(k\cdot u)^{\prime}=k\cdot u^{\prime}$		(2.283)
	$\displaystyle(u\pm v)^{\prime}=u^{\prime}\pm v^{\prime}$		(2.284)
	$\displaystyle(uv)^{\prime}=u^{\prime}v+uv^{\prime}$		(2.285)
	$\displaystyle\left(\frac{u}{v}\right)^{\prime}=\frac{u^{\prime}v-uv^{\prime}}{%v^{2}}$		(2.286)
	$\displaystyle(k)^{\prime}=0$		(2.287)
	$\displaystyle(x)^{\prime}=1$		(2.288)
	$\displaystyle(x^{n})^{\prime}=nx^{n-1}$		(2.289)
	$\displaystyle(a^{x})^{\prime}=a^{x}\ln a$		(2.290)
	$\displaystyle(e^{x})^{\prime}=e^{x}$		(2.291)
	$\displaystyle(\log_{a}x)^{\prime}=\frac{1}{x\ln a}$		(2.292)
	$\displaystyle(\ln x)^{\prime}=\frac{1}{x}$		(2.293)

2.5.4 Exercícios resolvidos

ER 2.5.1.

Calcule a derivada em relação a $x$ da função

f(x)=(x^{2}+x)(1+x^{3})-2x^{2}.

(2.294)

Solução 0.

	$\displaystyle f^{\prime}(x)=\overbrace{\left[(x^{2}+x)(1+x^{3})-2x^{2}\right]^%{\prime}}^{(u-v)^{\prime}}$		(2.295)
	$\displaystyle\text{}\quad=\overbrace{\left[(x^{2}+x)(1+x^{3})\right]^{\prime}}%^{(uv)^{\prime}}-\overbrace{(2x^{2})^{\prime}}^{(ku)^{\prime}}$		(2.296)
	$\displaystyle\text{}\quad=(x^{2}+x)^{\prime}(1+x^{3})+(x^{2}+x)(1+x^{3})^{%\prime}-2(x^{2})^{\prime}$		(2.297)
	$\displaystyle\text{}\quad=(2x+1)(1+x^{3})+(x^{2}+x)3x^{2}-4x$		(2.298)
	$\displaystyle\text{}\quad=2x+2x^{4}+1+x^{3}+3x^{4}+3x^{3}-4x$		(2.299)
	$\displaystyle\text{}\quad=5x^{4}+4x^{3}-2x+1.$		(2.300)

Com o SymPy, podemos computar esta derivada com os seguintes comandos:

⬇

1 from sympy import *

2 x = Symbol('x')

3 d = diff((x**2+x)*(1+x**3)-2x^2,x)

4 simplify(d)

ER 2.5.2.

Calcule

\frac{\mathrm{d}}{\mathrm{d}x}\left(\frac{x^{2}+x}{1-x^{3}}\right).

(2.301)

Solução 0.

Da regra de derivação do quociente, temos

	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\left(\frac{x^{2}+x}{1-x^{3}}\right%)=\frac{(x^{2}+x)^{\prime}(1-x^{3})-(x^{2}+x)(1-x^{3})^{\prime}}{(1-x^{3})^{2}}$		(2.302)
	$\displaystyle\text{}\quad=\frac{(2x+1)(1-x^{3})+(x^{2}+x)3x^{2}}{1-2x^{3}+x^{6}}$		(2.303)
	$\displaystyle\text{}\quad=\frac{2x-2x^{4}+1-x^{3}+3x^{4}+3x^{3}}{1-2x^{3}+x^{6}}$		(2.304)
	$\displaystyle\text{}\quad=\frac{x^{4}+2x^{3}+2x+1}{x^{6}-2x^{3}+1}$		(2.305)

Com o SymPy, podemos computar esta derivada com os seguintes comandos:

⬇

1 from sympy import *

2 x = Symbol('x')

3 d = diff((x**2+x)/(1-x**3),x)

4 simplify(d)

ER 2.5.3.

Encontre a equação da reta tangente ao gráfico de $f(x)=xe^{-x}$ no ponto $x=1$ .

Solução 0.

A equação da reta tangente ao gráfico de uma função $f$ no ponto $x=x_{0}$ é

y=f^{\prime}(x_{0})(x-x_{0})+f(x_{0}).

(2.306)

No caso, temos $f(x)=xe^{-x}$ e $x_{0}=1$ . Calculamos

	$\displaystyle f^{\prime}(x)=[xe^{-x}]^{\prime}=\left[\frac{x}{e^{x}}\right]$		(2.307)
	$\displaystyle\text{}\quad=\frac{(x)^{\prime}e^{x}-x(e^{x})^{\prime}}{(e^{x})^{%2}}$		(2.308)
	$\displaystyle\text{}\quad=\frac{e^{x}-xe^{x}}{e^{2x}}$		(2.309)
	$\displaystyle\text{}\quad=\frac{(1-x)e^{x}}{e^{2x}}$		(2.310)
	$\displaystyle\text{}\quad=(1-x)e^{x}e^{-2x}=(1-x)e^{-x}.$		(2.311)

Logo, a equação da reta tangente é

	$\displaystyle y=f^{\prime}(1)(x-1)+f(1)$		(2.312)
	$\displaystyle y=0\cdot(x-1)+e^{-1}$		(2.313)
	$\displaystyle y=\frac{1}{e}.$		(2.314)

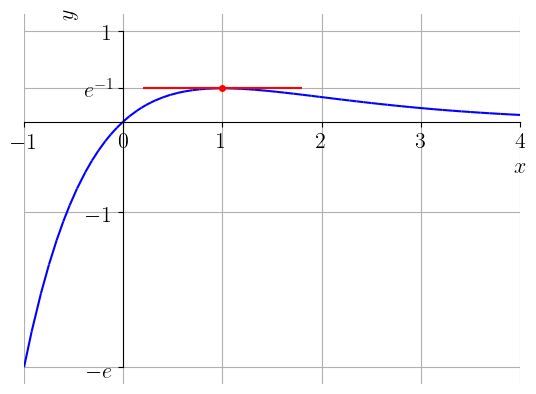
Na Figura 2.7, temos os esboços dos gráfico da função $f$ e sua reta tangente no ponto $x=1$ .

Refer to caption — Figura 2.7: Esboço da reta tangente ao gráfico de $f(x)=xe^{-x}$ no ponto $x=1$ .

Com o SymPy, podemos computar a expressão desta reta tangente com os seguintes comandos:

⬇

1 from sympy import *

2 x = Symbol('x')

3 f = x*exp(-x)

4 x0 = 1

5 fl = diff(f,x)

6 # y =

7 fl.subs(x,1)*(x-1)+f.subs(x,1)

2.5.5 Exercícios

E. 2.5.1.

Calcule a derivada em relação a $x$ das seguintes funções:

a)

$\displaystyle f(x)=5x^{3}$
b)

$\displaystyle g(x)=2e^{x}$
c)

$\displaystyle h(x)=\log 2x$
d)

$\displaystyle i(x)=\ln x^{2}$

Resposta 0.

a) $\displaystyle f^{\prime}(x)=15x^{2}$ ; b) $\displaystyle g^{\prime}(x)=2e^{x}$ ; c) $\displaystyle h^{\prime}(x)=\frac{\log 2}{x\ln 10}$ ; d) $\displaystyle i^{\prime}(x)=\frac{2}{x}$

E. 2.5.2.

Calcule a derivada em relação a $x$ das seguintes funções:

a)

$\displaystyle f(x)=2-5x^{3}$
b)

$\displaystyle g(x)=x^{4}-x^{2}+3x-1$
c)

$\displaystyle h(x)=3\cdot 2^{x}-\log_{2}x$

Resposta 0.

a) $\displaystyle f^{\prime}(x)=-15x^{2}$ ; b) $\displaystyle g^{\prime}(x)=4x^{3}-2x+3$ ; c) $\displaystyle h^{\prime}(x)=3\cdot 2^{x}\ln 2-\frac{1}{x\cdot\ln 2}$

E. 2.5.3.

Calcule a derivada em relação a $x$ das seguintes funções:

a)

$\displaystyle f(x)=(2x-1)(x^{2}-3x+1)$
b)

$\displaystyle g(x)=x\sqrt{x}$
c)

$\displaystyle h(x)=xe^{x}$
d)

$\displaystyle i(x)=e^{x}\ln x$

Resposta 0.

a) $\displaystyle f^{\prime}(x)=6x^{2}-14x+5$ ; b) $\displaystyle g^{\prime}(x)=\frac{3}{2}\sqrt{x}$ ; c) $\displaystyle h^{\prime}(x)=(x+1)e^{x}$ ; d) $\displaystyle i^{\prime}(x)=e^{x}\ln x+\frac{e^{x}}{x}$

E. 2.5.4.

Calcule a derivada em relação a $x$ das seguintes funções:

a)

$\displaystyle f(x)=\frac{x^{2}-1}{x-1}$
b)

$\displaystyle g(x)=\frac{x+1}{x-3}$
c)

$\displaystyle h(x)=\frac{x^{2}-1}{e^{x}}$

Resposta 0.

a) $\displaystyle f^{\prime}(x)=1$ ; b) $\displaystyle g^{\prime}(x)=\frac{-4}{(x-3)^{2}}$ ; c) $\displaystyle h^{\prime}(x)=(1+2x-x^{2})e^{-x}$

E. 2.5.5.

Calcule a derivada em relação a $x$ das seguintes funções:

a)

$\displaystyle f(x)=x^{2}e^{x}-\sqrt{x}$
b)

$\displaystyle g(x)=x\ln x-\frac{x-2}{x^{2}-x}$

Resposta 0.

a) $\displaystyle f^{\prime}(x)=(x^{2}+2x)e^{x}-\frac{1}{2\sqrt{x}}$ ; b) $\displaystyle g^{\prime}(x)=\ln x+1-\frac{x^{2}-x-(x-2)(2x-1)}{(x^{2}-x)^{2}}$

E. 2.5.6.

Calcule a derivada em relação a $x$ das seguintes funções:

a)

$f(x)=xe^{2x}$
b)

$g(x)=xe^{-2x}$

Resposta 0.

a) $f^{\prime}(x)=(1+2x)e^{2x}$ ; b) $g^{\prime}(x)=(1-2x)e^{-2x}$

E. 2.5.7.

Calcule a derivada em relação a $x$ das seguintes funções:

a)

$f(x)=x\ln x^{2}$
b)

$g(x)=x\ln x^{2}e^{x}$

Resposta 0.

a) $f^{\prime}(x)=\ln x^{2}+2$ ; b) $g^{\prime}(x)=2+2x+\ln x^{2}$

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Cálculo I

2 Derivadas 2.4 Derivada de Funções Exponenciais e Logarítmicas 2.6 Derivadas de funções trigonométricas

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

2.5 Regas Básicas de Derivação

2.5.1 Regras da multiplicação por constante e da soma

Sejam $k$ um número real, $u=u(x)$ e $v=v(x)$ funções deriváveis. Temos as seguintes regras básicas de derivação:

•

$\boldsymbol{(k\cdot u)^{\prime}=k\cdot u^{\prime}}$ .

De fato, pela definição da derivada temos

$\displaystyle(k\cdot u)^{\prime}(x)=\lim_{h\to 0}\frac{k\cdot u(x+h)-k\cdot u(%x)}{h}$ (2.239)

$\displaystyle\text{}\quad=\lim_{h\to 0}k\cdot\left(\frac{u(x+h)-u(x)}{h}\right)$ (2.240)

$\displaystyle\text{}\quad=k\cdot\lim_{h\to 0}\cancelto{u^{\prime}}{\frac{u(x+h%)-u(x)}{h}}$ (2.241)

$\displaystyle\text{}\quad=k\cdot u^{\prime}.$ (2.242)

No SymPy, podemos usar os seguintes comandos para obtermos esta regra de derivação:

⬇

1 from sympy import *

2 k = Symbol('k', real=True)

3 u = Function('u', real=True)

4 diff(k*u(x),x)

•

$\boldsymbol{(u\pm v)^{\prime}=u^{\prime}\pm v^{\prime}}$ .

De fato, temos

	$\displaystyle(u+v)^{\prime}(x)=\lim_{h\to 0}\frac{(u+v)(x+h)-(u+v)(x)}{h}$		(2.243)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{u(x+h)+v(x+h)-[u(x)+v(x)]}{h}$		(2.244)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\left[\cancelto{u^{\prime}}{\frac{u(x+h%)-u(x)}{h}}\right.$		(2.245)
	$\displaystyle\text{}\qquad+\left.\cancelto{v^{\prime}}{\frac{v(x+h)-v(x)}{h}}\right]$		(2.246)
	$\displaystyle\text{}\quad=u^{\prime}(x)+v^{\prime}(x).$		(2.247)

Também, como $(-v)^{\prime}=(-1\cdot v)^{\prime}=-1\cdot v^{\prime}=-v^{\prime}$ , temos

(u-v)^{\prime}=[u+(-v)]^{\prime}=u^{\prime}+(-v)^{\prime}=u^{\prime}-v^{\prime}.

(2.248)

No SymPy, podemos usar os seguintes comandos para obtermos a regra de derivação para soma:

⬇

1 from sympy import *

2 u = Function('u', real=True)

3 v = Function('v', real=True)

4 diff(u(x)+v(x),x)

Exemplo 2.5.1.

Vejamos os seguintes casos:

a)

$f(x)=2x$ .

Para calcularmos $f^{\prime}$ , podemos identificar $f=k\cdot u$ , com $k=2$ e $u(x)=x$ . Então, usando a regra da multiplicação por constante $(ku)^{\prime}=ku^{\prime}$ , temos

$f^{\prime}(x)=(2x)^{\prime}=2(x^{\prime})=2\cdot 1=2.$ (2.249)

No SymPy, podemos computar esta derivada com o comando:

⬇

1 from sympy import *

2 x = Symbol('x')

3 diff(2*x,x)
b)

$f(x)=2x+3$ .

Observamos que $f=u+v$ , com $u(x)=2x$ e $v(x)\equiv 3$ . Então, da regra da soma $(u+v)^{\prime}=u^{\prime}+v^{\prime}$ , temos

$f^{\prime}(x)=(2x+3)^{\prime}=(2x)^{\prime}+(3)^{\prime}=2+0=2.$ (2.250)

No SymPy, podemos computar esta derivada com o comando:

⬇

1 from sympy import *

2 x = Symbols('x')

3 diff(2*x+3,x)
c)

$f(x)=e^{x}-x^{2}$ .

Observamos que $f=u-v$ , com $u(x)=e^{x}$ e $v(x)=x^{2}$ . Usando a regra da subtração $(u-v)^{\prime}=u^{\prime}-v^{\prime}$ temos

$f^{\prime}(x)=(e^{x}-x^{2})^{\prime}=(e^{x})^{\prime}-(x^{2})^{\prime}=e^{x}-2x.$ (2.251)

No SymPy, podemos computar esta derivada com o comando:

⬇

1 from sympy import *

2 x = Symbols('x')

3 diff(exp(x)-x**2,x)

2.5.2 Regras do produto e do quociente

Sejam $y=u(x)$ e $y=v(x)$ funções deriváveis. Então:

•

$\boldsymbol{(u\cdot v)^{\prime}=u^{\prime}\cdot v+u\cdot v^{\prime}}$ .

De fato, da definição da derivada temos

	$\displaystyle(uv)^{\prime}(x)=\lim_{h\to 0}\frac{(uv)(x+h)-(uv)(x)}{h}$		(2.252)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{u(x+h)v(x+h)-u(x)v(x)}{h}$		(2.253)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\left[\frac{u(x+h)v(x+h)-u(x)v(x+h)}{h}\right.$		(2.254)
	$\displaystyle\text{}\qquad+\left.\frac{u(x)v(x+h)-u(x)v(x)}{h}\right]$		(2.255)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{u(x+h)-u(x)}{h}v(v+h)$		(2.256)
	$\displaystyle\text{}\qquad+\lim_{h\to 0}u(x)\frac{v(x+h)-v(x)}{h}$		(2.257)
	$\displaystyle\text{}\quad=u^{\prime}(x)v(x)+u(x)v^{\prime}(x).$		(2.258)

No SymPy, podemos usar os seguintes comandos para obtermos tal regra de derivação:

⬇

1 u = Function('u', real=True)

2 v = Function('v', real=True)

3 diff(u(x)*v(x), x)

•

$\displaystyle\boldsymbol{\left(\frac{u}{v}\right)^{\prime}=\frac{u^{\prime}v-%uv^{\prime}}{v^{2}}}$ , no caso de $v(x)\neq 0$ .

De fato, da definição de derivada temos

	$\displaystyle\left(\frac{u}{v}\right)^{\prime}(x)=\lim_{h\to 0}\frac{\left(%\frac{u}{v}\right)(x+h)-\left(\frac{u}{v}\right)(x)}{h}$		(2.259)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{\frac{u(x+h)v(x)-u(x)v(x+h)}{v(x+%h)v(x)}}{h}$		(2.260)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\left[\frac{u(x+h)v(x)-u(x)v(x)}{h}\right.$		(2.261)
	$\displaystyle\text{}\qquad-\left.\frac{u(x)v(x+h)-u(x)v(x)}{h}\right]\frac{1}{%v(x)v(x+h)}$		(2.262)
	$\displaystyle\text{}\quad=\left[\lim_{h\to 0}\cancelto{u^{\prime}(x)v(x)}{%\frac{u(x+h)-u(x)}{h}v(x)}\right.$		(2.263)
	$\displaystyle\text{}\qquad\left.-\lim_{h\to 0}\cancelto{u(x)v^{\prime}(x)}{u(x%)\frac{v(x+h)-v(x)}{h}}\right]\lim_{h\to 0}\cancelto{\frac{1}{v^{2}(x)}}{\frac%{1}{v(x)v(x+h)}}$		(2.264)
	$\displaystyle\text{}\quad=\frac{u^{\prime}(x)v(x)-u(x)v^{\prime}(x)}{v^{2}(x)}.$		(2.265)

No SymPy, podemos usar os seguintes comandos para obtermos tal regra de derivação:

⬇

1 from sympy import *

2 x = Symbol('x')

3 u = Function('u', real=True)

4 v = Function('v', real=True)

5 simplify(diff(u(x)/v(x),x))

Exemplo 2.5.2.

Vamos calcular a derivada em relação a $x$ da função $f(x)=x^{2}(x-1)$ de duas formas.

1.

Por expansão da expressão e utilização da regra da subtração.

$\displaystyle f^{\prime}(x)=[x^{2}(x-1)]^{\prime}$ (2.266)

$\displaystyle\text{}\quad=(x^{3}-x^{2})^{\prime}$ (2.267)

$\displaystyle\text{}\quad=\overbrace{(x^{3})^{\prime}-(x^{2})^{\prime}}^{(u-v)%^{\prime}=u^{\prime}-v^{\prime}}$ (2.268)

$\displaystyle\text{}\quad=3x^{2}-2x,\quad\quad(x^{n})^{\prime}=nx^{n-1}.$ (2.269)
2.

Utilizando a regra do produto.

Observamos que $f=u\cdot v$ , com $u(x)=x^{2}$ e $v(x)=x-1$ . Então, da regra do produto $(uv)^{\prime}=u^{\prime}v+uv^{\prime}$ , com $u^{\prime}(x)=2x$ e $v^{\prime}(x)=1$ , temos

$\displaystyle f^{\prime}(x)=[\overbrace{x^{2}}^{u}\overbrace{(x-1)}^{v}]^{\prime}$ (2.270)

$\displaystyle\text{}\quad=\overbrace{2x\cdot(x-1)}^{u^{\prime}\cdot v}+%\overbrace{x^{2}\cdot 1}^{u\cdot v^{\prime}}$ (2.271)

$\displaystyle\text{}\quad=2x^{2}-2x+x^{2}$ (2.272)

$\displaystyle\text{}\quad=3x^{2}-2x.$ (2.273)

Exemplo 2.5.3.

	$\displaystyle f^{\prime}(x)=\left(\frac{1}{x^{2}}\right)^{\prime}$		(2.274)
	$\displaystyle\text{}\quad=\frac{0\cdot x^{2}-1\cdot 2x}{(x^{2})^{2}},\quad%\quad\left[\left(\frac{u}{v}\right)^{\prime}=\frac{u^{\prime}v-uv^{\prime}}{v^%{2}}\right]$		(2.275)
	$\displaystyle\text{}\quad=-\frac{2x}{x^{4}}=-\frac{2}{x^{3}}$		(2.276)
	$\displaystyle\text{}\quad=-2x^{-3}.$		(2.277)

Observação 2.5.1.

Com abuso de linguagem, temos

\boldsymbol{(x^{n})^{\prime}=nx^{n-1}},

(2.278)

Exemplo 2.5.4.

Voltando ao exemplo anterior (Exemplo 2.5.3), temos

\left(\frac{1}{x^{2}}\right)^{\prime}=\overbrace{(x^{-2})^{\prime}}^{(x^{n})^{%\prime}}=\overbrace{-2x^{-2-1}}^{nx^{n-1}}=-2x^{-3}.

(2.279)

Exemplo 2.5.5.

Vamos calcular a derivada em relação a $x$ de $f(x)=xe^{x}$ . Usando a regra do produto $(uv)^{\prime}=u^{\prime}v+uv^{\prime}$ com $u(x)=x$ e $v(x)=e^{x}$ , temos

$\displaystyle f^{\prime}(x)$	$\displaystyle=\overbrace{(xe^{x})^{\prime}}^{(uv)^{\prime}}$	(2.280)
	$\displaystyle=\overbrace{1\cdot e^{x}}^{u^{\prime}\cdot v}+\overbrace{x\cdot e%^{x}}^{u\cdot v^{\prime}}$	(2.281)
	$\displaystyle=(x+1)e^{x}.$	(2.282)

2.5.3 Lista de derivadas

	$\displaystyle(k\cdot u)^{\prime}=k\cdot u^{\prime}$		(2.283)
	$\displaystyle(u\pm v)^{\prime}=u^{\prime}\pm v^{\prime}$		(2.284)
	$\displaystyle(uv)^{\prime}=u^{\prime}v+uv^{\prime}$		(2.285)
	$\displaystyle\left(\frac{u}{v}\right)^{\prime}=\frac{u^{\prime}v-uv^{\prime}}{%v^{2}}$		(2.286)
	$\displaystyle(k)^{\prime}=0$		(2.287)
	$\displaystyle(x)^{\prime}=1$		(2.288)
	$\displaystyle(x^{n})^{\prime}=nx^{n-1}$		(2.289)
	$\displaystyle(a^{x})^{\prime}=a^{x}\ln a$		(2.290)
	$\displaystyle(e^{x})^{\prime}=e^{x}$		(2.291)
	$\displaystyle(\log_{a}x)^{\prime}=\frac{1}{x\ln a}$		(2.292)
	$\displaystyle(\ln x)^{\prime}=\frac{1}{x}$		(2.293)

2.5.4 Exercícios resolvidos

ER 2.5.1.

Calcule a derivada em relação a $x$ da função

f(x)=(x^{2}+x)(1+x^{3})-2x^{2}.

(2.294)

Solução 0.

	$\displaystyle f^{\prime}(x)=\overbrace{\left[(x^{2}+x)(1+x^{3})-2x^{2}\right]^%{\prime}}^{(u-v)^{\prime}}$		(2.295)
	$\displaystyle\text{}\quad=\overbrace{\left[(x^{2}+x)(1+x^{3})\right]^{\prime}}%^{(uv)^{\prime}}-\overbrace{(2x^{2})^{\prime}}^{(ku)^{\prime}}$		(2.296)
	$\displaystyle\text{}\quad=(x^{2}+x)^{\prime}(1+x^{3})+(x^{2}+x)(1+x^{3})^{%\prime}-2(x^{2})^{\prime}$		(2.297)
	$\displaystyle\text{}\quad=(2x+1)(1+x^{3})+(x^{2}+x)3x^{2}-4x$		(2.298)
	$\displaystyle\text{}\quad=2x+2x^{4}+1+x^{3}+3x^{4}+3x^{3}-4x$		(2.299)
	$\displaystyle\text{}\quad=5x^{4}+4x^{3}-2x+1.$		(2.300)

Com o SymPy, podemos computar esta derivada com os seguintes comandos:

⬇

1 from sympy import *

2 x = Symbol('x')

3 d = diff((x**2+x)*(1+x**3)-2x^2,x)

4 simplify(d)

ER 2.5.2.

Calcule

\frac{\mathrm{d}}{\mathrm{d}x}\left(\frac{x^{2}+x}{1-x^{3}}\right).

(2.301)

Solução 0.

Da regra de derivação do quociente, temos

	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\left(\frac{x^{2}+x}{1-x^{3}}\right%)=\frac{(x^{2}+x)^{\prime}(1-x^{3})-(x^{2}+x)(1-x^{3})^{\prime}}{(1-x^{3})^{2}}$		(2.302)
	$\displaystyle\text{}\quad=\frac{(2x+1)(1-x^{3})+(x^{2}+x)3x^{2}}{1-2x^{3}+x^{6}}$		(2.303)
	$\displaystyle\text{}\quad=\frac{2x-2x^{4}+1-x^{3}+3x^{4}+3x^{3}}{1-2x^{3}+x^{6}}$		(2.304)
	$\displaystyle\text{}\quad=\frac{x^{4}+2x^{3}+2x+1}{x^{6}-2x^{3}+1}$		(2.305)

Com o SymPy, podemos computar esta derivada com os seguintes comandos:

⬇

1 from sympy import *

2 x = Symbol('x')

3 d = diff((x**2+x)/(1-x**3),x)

4 simplify(d)

ER 2.5.3.

Encontre a equação da reta tangente ao gráfico de $f(x)=xe^{-x}$ no ponto $x=1$ .

Solução 0.

A equação da reta tangente ao gráfico de uma função $f$ no ponto $x=x_{0}$ é

y=f^{\prime}(x_{0})(x-x_{0})+f(x_{0}).

(2.306)

No caso, temos $f(x)=xe^{-x}$ e $x_{0}=1$ . Calculamos

	$\displaystyle f^{\prime}(x)=[xe^{-x}]^{\prime}=\left[\frac{x}{e^{x}}\right]$		(2.307)
	$\displaystyle\text{}\quad=\frac{(x)^{\prime}e^{x}-x(e^{x})^{\prime}}{(e^{x})^{%2}}$		(2.308)
	$\displaystyle\text{}\quad=\frac{e^{x}-xe^{x}}{e^{2x}}$		(2.309)
	$\displaystyle\text{}\quad=\frac{(1-x)e^{x}}{e^{2x}}$		(2.310)
	$\displaystyle\text{}\quad=(1-x)e^{x}e^{-2x}=(1-x)e^{-x}.$		(2.311)

Logo, a equação da reta tangente é

	$\displaystyle y=f^{\prime}(1)(x-1)+f(1)$		(2.312)
	$\displaystyle y=0\cdot(x-1)+e^{-1}$		(2.313)
	$\displaystyle y=\frac{1}{e}.$		(2.314)

Na Figura 2.7, temos os esboços dos gráfico da função $f$ e sua reta tangente no ponto $x=1$ .

Com o SymPy, podemos computar a expressão desta reta tangente com os seguintes comandos:

⬇

1 from sympy import *

2 x = Symbol('x')

3 f = x*exp(-x)

4 x0 = 1

5 fl = diff(f,x)

6 # y =

7 fl.subs(x,1)*(x-1)+f.subs(x,1)

2.5.5 Exercícios

E. 2.5.1.

Calcule a derivada em relação a $x$ das seguintes funções:

a)

$\displaystyle f(x)=5x^{3}$
b)

$\displaystyle g(x)=2e^{x}$
c)

$\displaystyle h(x)=\log 2x$
d)

$\displaystyle i(x)=\ln x^{2}$

Resposta 0.

a) $\displaystyle f^{\prime}(x)=15x^{2}$ ; b) $\displaystyle g^{\prime}(x)=2e^{x}$ ; c) $\displaystyle h^{\prime}(x)=\frac{\log 2}{x\ln 10}$ ; d) $\displaystyle i^{\prime}(x)=\frac{2}{x}$

E. 2.5.2.

Calcule a derivada em relação a $x$ das seguintes funções:

a)

$\displaystyle f(x)=2-5x^{3}$
b)

$\displaystyle g(x)=x^{4}-x^{2}+3x-1$
c)

$\displaystyle h(x)=3\cdot 2^{x}-\log_{2}x$

Resposta 0.

a) $\displaystyle f^{\prime}(x)=-15x^{2}$ ; b) $\displaystyle g^{\prime}(x)=4x^{3}-2x+3$ ; c) $\displaystyle h^{\prime}(x)=3\cdot 2^{x}\ln 2-\frac{1}{x\cdot\ln 2}$

E. 2.5.3.

Calcule a derivada em relação a $x$ das seguintes funções:

a)

$\displaystyle f(x)=(2x-1)(x^{2}-3x+1)$
b)

$\displaystyle g(x)=x\sqrt{x}$
c)

$\displaystyle h(x)=xe^{x}$
d)

$\displaystyle i(x)=e^{x}\ln x$

Resposta 0.

E. 2.5.4.

Calcule a derivada em relação a $x$ das seguintes funções:

a)

$\displaystyle f(x)=\frac{x^{2}-1}{x-1}$
b)

$\displaystyle g(x)=\frac{x+1}{x-3}$
c)

$\displaystyle h(x)=\frac{x^{2}-1}{e^{x}}$

Resposta 0.

a) $\displaystyle f^{\prime}(x)=1$ ; b) $\displaystyle g^{\prime}(x)=\frac{-4}{(x-3)^{2}}$ ; c) $\displaystyle h^{\prime}(x)=(1+2x-x^{2})e^{-x}$

E. 2.5.5.

Calcule a derivada em relação a $x$ das seguintes funções:

a)

$\displaystyle f(x)=x^{2}e^{x}-\sqrt{x}$
b)

$\displaystyle g(x)=x\ln x-\frac{x-2}{x^{2}-x}$

Resposta 0.

a) $\displaystyle f^{\prime}(x)=(x^{2}+2x)e^{x}-\frac{1}{2\sqrt{x}}$ ; b) $\displaystyle g^{\prime}(x)=\ln x+1-\frac{x^{2}-x-(x-2)(2x-1)}{(x^{2}-x)^{2}}$

E. 2.5.6.

Calcule a derivada em relação a $x$ das seguintes funções:

a)

$f(x)=xe^{2x}$
b)

$g(x)=xe^{-2x}$

Resposta 0.

a) $f^{\prime}(x)=(1+2x)e^{2x}$ ; b) $g^{\prime}(x)=(1-2x)e^{-2x}$

E. 2.5.7.

Calcule a derivada em relação a $x$ das seguintes funções:

a)

$f(x)=x\ln x^{2}$
b)

$g(x)=x\ln x^{2}e^{x}$

Resposta 0.

a) $f^{\prime}(x)=\ln x^{2}+2$ ; b) $g^{\prime}(x)=2+2x+\ln x^{2}$

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Pedro H A Konzen

| | | |

	$\displaystyle(k\cdot u)^{\prime}(x)=\lim_{h\to 0}\frac{k\cdot u(x+h)-k\cdot u(%x)}{h}$		(2.239)
	$\displaystyle\text{}\quad=\lim_{h\to 0}k\cdot\left(\frac{u(x+h)-u(x)}{h}\right)$		(2.240)
	$\displaystyle\text{}\quad=k\cdot\lim_{h\to 0}\cancelto{u^{\prime}}{\frac{u(x+h%)-u(x)}{h}}$		(2.241)
	$\displaystyle\text{}\quad=k\cdot u^{\prime}.$		(2.242)

	$\displaystyle f^{\prime}(x)=[x^{2}(x-1)]^{\prime}$		(2.266)
	$\displaystyle\text{}\quad=(x^{3}-x^{2})^{\prime}$		(2.267)
	$\displaystyle\text{}\quad=\overbrace{(x^{3})^{\prime}-(x^{2})^{\prime}}^{(u-v)%^{\prime}=u^{\prime}-v^{\prime}}$		(2.268)
	$\displaystyle\text{}\quad=3x^{2}-2x,\quad\quad(x^{n})^{\prime}=nx^{n-1}.$		(2.269)

	$\displaystyle f^{\prime}(x)=[\overbrace{x^{2}}^{u}\overbrace{(x-1)}^{v}]^{\prime}$		(2.270)
	$\displaystyle\text{}\quad=\overbrace{2x\cdot(x-1)}^{u^{\prime}\cdot v}+%\overbrace{x^{2}\cdot 1}^{u\cdot v^{\prime}}$		(2.271)
	$\displaystyle\text{}\quad=2x^{2}-2x+x^{2}$		(2.272)
	$\displaystyle\text{}\quad=3x^{2}-2x.$		(2.273)