Política de uso de dados

Ao navegar por este site, você concorda com a política de uso de dados.

Política de uso de dados

Ao navegar por este site, você concorda com a política de uso de dados.

| | | |

Cálculo I

2 Derivadas 2.1 Derivada no ponto 2.3 Derivada de Funções Constante, Identidade e Potência

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

2.2 Função derivada

A derivada de uma função $f$ em relação à variável $x$ é a função $\displaystyle f^{\prime}=\frac{\mathrm{d}f}{\mathrm{d}x}$ cujo valor em $x$ é

f^{\prime}(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h},

(2.73)

quando este limite existe. Dizemos que $f$ é derivável (ou diferenciável) em um ponto $x$ de seu domínio, quando o limite dado em (2.73) existe. Se isso ocorre para todo número real $x$ , dizemos que $f$ é derivável em toda parte.

Exemplo 2.2.1.

A derivada de $f(x)=x^{2}$ é

	$\displaystyle f^{\prime}(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$		(2.74)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{(x+h)^{2}-x^{2}}{h}$		(2.75)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{x^{2}+2xh+h^{2}-x^{2}}{h}$		(2.76)
	$\displaystyle\text{}\quad=\lim_{h\to 0}2x+h=2x.$		(2.77)

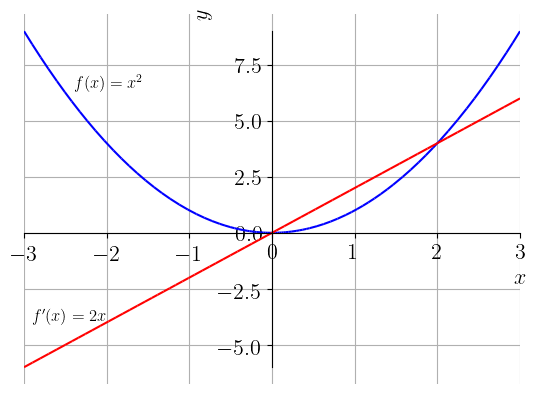
Observamos que este é o caso de uma função derivável em toda parte.A Figura 2.4.

Refer to caption — Figura 2.4: Esboços dos gráficos da função $f(x)=x^{2}$ e de sua derivada $f^{\prime}(x)=2x$ .

Com o SymPy, podemos usar os seguintes comandos para verificarmos este resultado:

⬇

1 from sympy import *

2 x,h = symbols('x,h')

3 f = lambda x: x**2

4 limit((f(x+h)-f(x))/h,h,0)

Mais adequadamente, podemos usar o comando:

⬇

1 diff(x**2,x)

ou, equivalentemente,

⬇

1 diff(x**2)

para computar a derivada de $x^{2}$ em relação a $x$ .

Observação 2.2.1.

A derivada à direita (à esquerda) de uma função $f$ em um ponto $x$ é definida por

f_{\pm}^{\prime}(x)=\frac{\mathrm{d}f}{\mathrm{d}x^{\pm}}=\lim_{h\to 0^{\pm}}% \frac{f(x+h)-f(x)}{h}.

(2.78)

Desta forma, no caso de pontos extremos do domínio de uma função, empregamos a derivada lateral correspondente.

Exemplo 2.2.2.

Vamos calcular a derivada de $f(x)=\sqrt{x}$ . Para $x=0$ , só faz sentido calcular a derivada lateral à direta:

	$\displaystyle f^{\prime}_{+}(0)=\lim_{h\to 0^{+}}\frac{\sqrt{0+h}-\sqrt{0}}{h}$		(2.79)
	$\displaystyle\text{}\quad=\lim_{h\to 0^{+}}\frac{\sqrt{h}}{h}$		(2.80)
	$\displaystyle\text{}\quad=\lim_{h\to 0^{+}}\frac{1}{\cancelto{0^{+}}{\sqrt{h}}% }=+\infty.$		(2.81)

Ou seja, $f(x)=\sqrt{x}$ não é derivável em $x=0$ . Agora, para $x>0$ , temos

	$\displaystyle f^{\prime}(x)=\lim_{h\to 0}\frac{\sqrt{x+h}-\sqrt{x}}{h}$		(2.82)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{\sqrt{x+h}-\sqrt{x}}{h}\cdot\frac% {\sqrt{x+h}+\sqrt{x}}{\sqrt{x+h}+\sqrt{x}}$		(2.83)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{x+h-x}{h(\sqrt{x+h}+\sqrt{x})}$		(2.84)
	$\displaystyle\text{}\quad=\frac{1}{2\sqrt{x}}.$		(2.85)

Na Figura 2.5, temos os esboços dos gráficos desta função e de sua derivada.

No SymPy, a computação de $f^{\prime}_{+}(0)$ pode ser feita com os comandos¹³¹³endnote: ¹³Por padrão no SymPy, o limite é tomado à direita.:

⬇

1 from sympy import *

2 h = Symbol('h')

3 limit((sqrt(0+h)-sqrt(0))/h,h,0)

E, a derivada de $f(x)=\sqrt{x}$ (nos pontos de diferenciabilidade) pode ser obtida com o comando:

⬇

1 diff(sqrt(x),x)

Exemplo 2.2.3.

A função valor absoluto é derivável para todo $x\neq 0$ e não é derivável em $x=0$ . De fato, para $x<0$ temos

	$\displaystyle f^{\prime}(x)=\lim_{h\to 0}\frac{\|x+h\|-\|x\|}{h}$		(2.86)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{-(x+h)+x}{h}$		(2.87)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{h}{h}=1.$		(2.88)

Analogamente, para $x>0$ temos

	$\displaystyle f^{\prime}(x)=\lim_{h\to 0}\frac{\|x+h\|-\|x\|}{h}$		(2.89)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{x+h-x}{h}$		(2.90)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{h}{h}=1.$		(2.91)

Agora, para $x=0$ , devemos verificar as derivadas laterais:

	$\displaystyle f^{\prime}_{+}(0)=\lim_{h\to 0^{+}}\frac{\|h\|-\|0\|}{h}=\lim_{h\to 0% ^{+}}\frac{h}{h}=1,$		(2.92)
	$\displaystyle f^{\prime}_{-}(0)=\lim_{h\to 0^{-}}\frac{\|h\|-\|0\|}{h}=\lim_{h\to 0% ^{-}}\frac{-h}{h}=-1.$		(2.93)

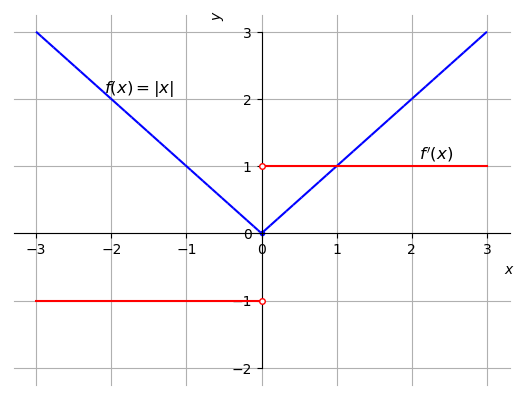
Como as derivadas laterais são diferentes, temos que $y=|x|$ não é derivável em $x=0$ . Na figura 2.6, temos os esboços dos gráficos de $f(x)=|x|$ e sua derivada

f^{\prime}(x)=\left\{\begin{array}[H]{rr}-1&,x<0,\\ 1&,x>0\end{array}\right.

(2.94)

Esta é chamada de função sinal e denotada por $\operatorname{sign}(x)$ . Ou seja, a função sinal é a derivada da função valor absoluto.

No SymPy, podemos computar a derivada da função valor absoluto com o comando:

⬇

1 In : from sympy import *

2 ...: x = symbols('x', real=True)

3 ...: diff(abs(x))

4 Out: sign(x)

2.2.1 Continuidade de uma função derivável

Uma função $y=f(x)$ derivável em $x=x_{0}$ é contínua neste ponto. De fato, lembramos que $f$ é contínua em $x=x_{0}$ quando $x_{0}$ é um ponto de seu domínio e

\lim_{x\to x_{0}}f(x)=f(x_{0}).

(2.95)

Isto é equivalente a

\lim_{h\to 0}f(x_{0}+h)=f(x_{0})

(2.96)

ou, ainda,

\lim_{h\to 0}\left[f(x_{0}+h)-f(x_{0})\right]=0.

(2.97)

Vamos mostrar que este é o caso quando $f$ é derivável em $x=x_{0}$ . Neste caso, temos

	$\displaystyle\lim_{h\to 0}\left[f(x_{0}+h)-f(x_{0})\right]=\lim_{h\to 0}\left[% f(x_{0}+h)-f(x_{0})\right]\cdot\frac{h}{h}$		(2.98)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\left[\cancelto{f^{\prime}(x_{0})}{% \frac{f(x_{0}+h)-f(x_{0})}{h}}\right]\cdot h$		(2.99)
	$\displaystyle\text{}\quad=\lim_{h\to 0}f^{\prime}(x_{0})\cdot h$		(2.100)
	$\displaystyle\text{}\quad=0.$		(2.101)

Ou seja, de fato, se $f$ é derivável em $x=x_{0}$ , então $f$ é contínua em $x=x_{0}$ .

Observação 2.2.2.

A recíproca não é verdadeira, uma função $f$ ser contínua em um ponto $x=x_{0}$ não garante que ela seja derivável em $x=x_{0}$ . No Exemplo 2.2.3, vimos que a função valor absoluto $f(x)=|x|$ não derivável em $x=0$ , enquanto esta função é contínua (veja, também, o Exemplo 1.6.2).

2.2.2 Derivadas de ordens mais altas

A derivada de uma função $y=f(x)$ em relação a $x$ é a função $y=f^{\prime}(x)$ . Quando esta é diferenciável, podemos calcular a derivada da derivada. Esta é conhecida como a segunda derivada de $f$ , denotamos

f^{\prime\prime}(x):=(f^{\prime}(x))^{\prime}\leavevmode\nobreak\ \text{ou}% \leavevmode\nobreak\ \frac{\mathrm{d}^{2}}{\mathrm{d}x^{2}}f(x)=\frac{\mathrm{% d}}{\mathrm{d}x}\left(\frac{\mathrm{d}}{\mathrm{d}x}f(x)\right).

(2.102)

Exemplo 2.2.4.

Seja $f(x)=x^{3}$ . Então, a primeira derivada de $f$ é

	$\displaystyle f^{\prime}(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$		(2.103)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{(x+h)^{3}-x^{3}}{h}$		(2.104)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{x^{3}+3x^{2}h+3xh^{2}+h^{3}-x^{3}% }{h}$		(2.105)
	$\displaystyle\text{}\quad=\lim_{h\to 0}3x^{2}+\cancelto{0}{3xh}+\cancelto{0}{h% ^{2}}=3x^{2}.$		(2.106)

De posse da primeira derivada $f^{\prime}(x)=3x^{2}$ , podemos calcular a segunda derivada de $f$ , como segue:

	$\displaystyle f^{\prime\prime}(x)=[f^{\prime}(x)]^{\prime}$		(2.107)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{f^{\prime}(x+h)-f^{\prime}(x)}{h}$		(2.108)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{3(x+h)^{2}-3x^{2}}{h}$		(2.109)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{3x^{2}+6xh+h^{2}-3x^{2}}{h}$		(2.110)
	$\displaystyle\text{}\quad=\lim_{h\to 0}6x+\cancelto{0}{h}=6x,$		(2.111)

i.e. $f^{\prime\prime}(x)=6x$ .

No SymPy, podemos computar a segunda derivada da função com o comando:

⬇

1 In : from sympy import *

2 ...: x = symbols('x')

3 ...: diff(x**3,x,2)

4 Out: 6*x

Generalizando, quando existe, a $n$ -ésima derivada de uma função $y=f(x)$ , $n\geq 1$ , é recursivamente definida (e denotada) por

f^{(n)}(x):=[f^{(n-1)}]^{\prime}\leavevmode\nobreak\ \text{ou}\leavevmode% \nobreak\ \frac{\mathrm{d}^{n}}{\mathrm{d}x^{n}}f(x):=\frac{\mathrm{d}}{% \mathrm{d}x}\left[\frac{\mathrm{d}^{n-1}}{\mathrm{d}x^{n-1}}f(x)\right],

(2.112)

com $f^{(3)}\equiv f^{\prime\prime\prime}$ , $f^{(2)}\equiv f^{\prime\prime}$ , $f^{(1)}\equiv f^{\prime}$ e $f^{(0)}\equiv f$ .

Exemplo 2.2.5.

A terceira derivada de $f(x)=x^{3}$ em relação a $x$ é $f^{\prime\prime\prime}(x)=[f^{\prime\prime}(x)]^{\prime}$ . No exemplo anterior (Exemplo 2.2.4), calculamos $f^{\prime\prime}(x)=6x$ . Logo,

	$\displaystyle f^{\prime\prime\prime}(x)=[6x]^{\prime}$		(2.113)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{6(x+h)-6x}{h}$		(2.114)
	$\displaystyle\text{}\quad=\lim_{h\to 0}6=6.$		(2.115)

A quarta derivada de $f(x)=x^{3}$ em relação a $x$ é $f^{(4)}(x)\equiv 0$ , bem como $f^{(5)}(x)\equiv 0$ . Verifique!

No SymPy, podemos computar a terceira derivada da função com o comando:

⬇

1 In : from sympy import *

2 ...: x = symbols('x')

3 ...: diff(x**3,x,3)

4 Out: 6

2.2.3 Exercícios resolvidos

ER 2.2.1.

Calcule a derivada da função $f(x)=x^{2}+2x+1$ em relação a $x$ .

Solução 0.

Por definição da derivada, temos

	$\displaystyle f^{\prime}(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$		(2.116)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{(x+h)^{2}+2(x+h)+1-(x^{2}+2x+1)}{h}$		(2.117)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{x^{2}+2xh+h^{2}+2x+2h+1-x^{2}-2x-% 1}{h}$		(2.118)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{2xh+h^{2}+2h}{h}$		(2.119)
	$\displaystyle\text{}\quad=\lim_{h\to 0}2x+h+2=2x+2.$		(2.120)

ER 2.2.2.

Determine os pontos de diferenciabilidade da função $f(x)=|x-1|$ .

Solução 0.

O gráfico da função $f(x)=|x-1|$ tem um bico no ponto $x=1$ (verifique!). Para valores de $x<1$ , temos

	$\displaystyle f^{\prime}(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$		(2.121)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{\|\overbrace{x+h-1}^{<0}\|-\|% \overbrace{x-1}^{<0}\|}{h}$		(2.122)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{-x-h+1+x-1}{h}$		(2.123)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{-h}{h}=-1.$		(2.124)

Para valores de $x>1$ , temos

	$\displaystyle f^{\prime}(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$		(2.125)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{\|\overbrace{x+h-1}^{>0}\|-\|% \overbrace{x-1}^{>0}\|}{h}$		(2.126)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{x+h-1-x+1}{h}$		(2.127)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{h}{h}=1.$		(2.128)

Ou seja, temos que $f(x)=|x-1|$ é diferenciável para $x\neq 1$ . Agora, para $x=1$ , temos

$\displaystyle f^{\prime}_{-}(x)=\lim_{h\to 0^{-}}\frac{f(1+h)-f(1)}{h}$		(2.129)
$\displaystyle\text{}\quad=\lim_{h\to 0^{-}}\frac{\|\overbrace{h}^{<0}\|-\|1-1\|}{h}$		(2.130)
$\displaystyle\text{}\quad=\lim_{h\to 0^{-}}\frac{-h}{h}=-1$		(2.131)
$\displaystyle f^{\prime}_{+}(x)$	$\displaystyle=\lim_{h\to 0^{+}}\frac{f(1+h)-f(1)}{h}$	(2.132)
$\displaystyle\text{}\quad=\lim_{h\to 0^{+}}\frac{\|\overbrace{h}^{>0}\|-\|1-1\|}{h}$		(2.133)
$\displaystyle\text{}\quad=\lim_{h\to 0^{+}}\frac{h}{h}=1$		(2.134)

Como $f^{\prime}_{-}(1)\neq f^{\prime}_{+}(1)$ , temos que $\nexists f^{\prime}(1)$ . Concluímos que $f(x)=|x-1|$ é diferenciável nos pontos $\mathbb{R}\setminus\{1\}$ .

ER 2.2.3.

Calcule a segunda derivada em relação a $x$ da função

f(x)=x-x^{2}.

(2.136)

Solução 0.

Começamos calculando a primeira derivada da função:

	$\displaystyle f^{\prime}(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$		(2.137)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{(x+h)-(x+h)^{2}-(x-x^{2})}{h}$		(2.138)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{x+h-x^{2}-2xh-h^{2}-x+x^{2}}{h}$		(2.139)
	$\displaystyle\text{}\quad=\lim_{h\to 0}1-2x-\cancelto{0}{h}=1-2x.$		(2.140)

Então, calculamos a segunda derivada como segue

	$\displaystyle f^{\prime\prime}(x)=[f^{\prime}(x)]^{\prime}$		(2.141)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{f^{\prime}(x+h)-f^{\prime}(x)}{h}$		(2.142)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{1-2(x+h)-(1-2x)}{h}$		(2.143)
	$\displaystyle\text{}\quad=\lim_{h\to 0}-2=-2.$		(2.144)

2.2.4 Exercícios

E. 2.2.1.

Calcule a derivada em relação a $x$ de cada uma das seguintes funções:

a)

$f(x)=2$
b)

$g(x)=-3$
c)

$h(x)=\sqrt{e}$

Resposta 0.

a) $0$ ; b) $0$ ; c) $0$

E. 2.2.2.

Calcule a derivada em relação a $x$ de cada uma das seguintes funções:

a)

$f(x)=2x$
b)

$g(x)=-3x$
c)

$h(x)=\sqrt{e}x$

Resposta 0.

a) $2$ ; b) $-3$ ; c) $\sqrt{e}$

E. 2.2.3.

Calcule a derivada em relação a $x$ da função

f(x)=x^{2}-2x+1.

(2.145)

Resposta 0.

$f^{\prime}(x)=2x-2$

E. 2.2.4.

Determine os pontos de diferenciabilidade da função $f(x)=\sqrt{x-1}$ .

Resposta 0.

$(1,\infty)$

E. 2.2.5.

Considerando

f(x)=x^{2}-x^{3},

(2.146)

calcule:

a)

$f^{\prime}(x)$
b)

$f^{\prime\prime}(x)$
c)

$f^{\prime\prime\prime}(x)$
d)

$f^{(4)}$
e)

$f^{(1001)}(x)$

Resposta 0.

a) $2x-3x^{2}$ ; b) $2-6x$ ; c) $-6$ ; d) $0$ ; e) $0$

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Cálculo I

2 Derivadas 2.1 Derivada no ponto 2.3 Derivada de Funções Constante, Identidade e Potência

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

2.2 Função derivada

A derivada de uma função $f$ em relação à variável $x$ é a função $\displaystyle f^{\prime}=\frac{\mathrm{d}f}{\mathrm{d}x}$ cujo valor em $x$ é

f^{\prime}(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h},

(2.73)

Exemplo 2.2.1.

A derivada de $f(x)=x^{2}$ é

	$\displaystyle f^{\prime}(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$		(2.74)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{(x+h)^{2}-x^{2}}{h}$		(2.75)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{x^{2}+2xh+h^{2}-x^{2}}{h}$		(2.76)
	$\displaystyle\text{}\quad=\lim_{h\to 0}2x+h=2x.$		(2.77)

Observamos que este é o caso de uma função derivável em toda parte.A Figura 2.4.

Com o SymPy, podemos usar os seguintes comandos para verificarmos este resultado:

⬇

1 from sympy import *

2 x,h = symbols('x,h')

3 f = lambda x: x**2

4 limit((f(x+h)-f(x))/h,h,0)

Mais adequadamente, podemos usar o comando:

⬇

1 diff(x**2,x)

ou, equivalentemente,

⬇

1 diff(x**2)

para computar a derivada de $x^{2}$ em relação a $x$ .

Observação 2.2.1.

A derivada à direita (à esquerda) de uma função $f$ em um ponto $x$ é definida por

f_{\pm}^{\prime}(x)=\frac{\mathrm{d}f}{\mathrm{d}x^{\pm}}=\lim_{h\to 0^{\pm}}% \frac{f(x+h)-f(x)}{h}.

(2.78)

Desta forma, no caso de pontos extremos do domínio de uma função, empregamos a derivada lateral correspondente.

Exemplo 2.2.2.

Vamos calcular a derivada de $f(x)=\sqrt{x}$ . Para $x=0$ , só faz sentido calcular a derivada lateral à direta:

	$\displaystyle f^{\prime}_{+}(0)=\lim_{h\to 0^{+}}\frac{\sqrt{0+h}-\sqrt{0}}{h}$		(2.79)
	$\displaystyle\text{}\quad=\lim_{h\to 0^{+}}\frac{\sqrt{h}}{h}$		(2.80)
	$\displaystyle\text{}\quad=\lim_{h\to 0^{+}}\frac{1}{\cancelto{0^{+}}{\sqrt{h}}% }=+\infty.$		(2.81)

Ou seja, $f(x)=\sqrt{x}$ não é derivável em $x=0$ . Agora, para $x>0$ , temos

	$\displaystyle f^{\prime}(x)=\lim_{h\to 0}\frac{\sqrt{x+h}-\sqrt{x}}{h}$		(2.82)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{\sqrt{x+h}-\sqrt{x}}{h}\cdot\frac% {\sqrt{x+h}+\sqrt{x}}{\sqrt{x+h}+\sqrt{x}}$		(2.83)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{x+h-x}{h(\sqrt{x+h}+\sqrt{x})}$		(2.84)
	$\displaystyle\text{}\quad=\frac{1}{2\sqrt{x}}.$		(2.85)

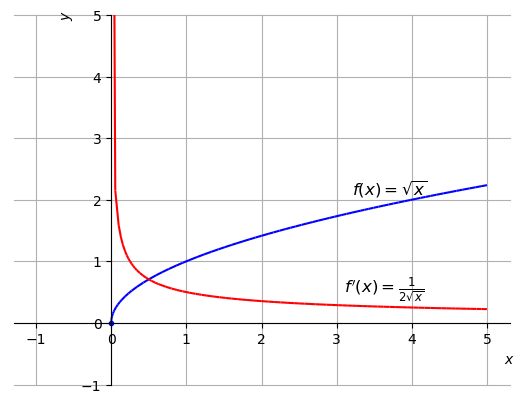
Na Figura 2.5, temos os esboços dos gráficos desta função e de sua derivada.

No SymPy, a computação de $f^{\prime}_{+}(0)$ pode ser feita com os comandos¹³¹³endnote: ¹³Por padrão no SymPy, o limite é tomado à direita.:

⬇

1 from sympy import *

2 h = Symbol('h')

3 limit((sqrt(0+h)-sqrt(0))/h,h,0)

E, a derivada de $f(x)=\sqrt{x}$ (nos pontos de diferenciabilidade) pode ser obtida com o comando:

⬇

1 diff(sqrt(x),x)

Exemplo 2.2.3.

A função valor absoluto é derivável para todo $x\neq 0$ e não é derivável em $x=0$ . De fato, para $x<0$ temos

	$\displaystyle f^{\prime}(x)=\lim_{h\to 0}\frac{\|x+h\|-\|x\|}{h}$		(2.86)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{-(x+h)+x}{h}$		(2.87)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{h}{h}=1.$		(2.88)

Analogamente, para $x>0$ temos

	$\displaystyle f^{\prime}(x)=\lim_{h\to 0}\frac{\|x+h\|-\|x\|}{h}$		(2.89)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{x+h-x}{h}$		(2.90)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{h}{h}=1.$		(2.91)

Agora, para $x=0$ , devemos verificar as derivadas laterais:

	$\displaystyle f^{\prime}_{+}(0)=\lim_{h\to 0^{+}}\frac{\|h\|-\|0\|}{h}=\lim_{h\to 0% ^{+}}\frac{h}{h}=1,$		(2.92)
	$\displaystyle f^{\prime}_{-}(0)=\lim_{h\to 0^{-}}\frac{\|h\|-\|0\|}{h}=\lim_{h\to 0% ^{-}}\frac{-h}{h}=-1.$		(2.93)

Como as derivadas laterais são diferentes, temos que $y=|x|$ não é derivável em $x=0$ . Na figura 2.6, temos os esboços dos gráficos de $f(x)=|x|$ e sua derivada

f^{\prime}(x)=\left\{\begin{array}[H]{rr}-1&,x<0,\\ 1&,x>0\end{array}\right.

(2.94)

Esta é chamada de função sinal e denotada por $\operatorname{sign}(x)$ . Ou seja, a função sinal é a derivada da função valor absoluto.

No SymPy, podemos computar a derivada da função valor absoluto com o comando:

⬇

1 In : from sympy import *

2 ...: x = symbols('x', real=True)

3 ...: diff(abs(x))

4 Out: sign(x)

2.2.1 Continuidade de uma função derivável

Uma função $y=f(x)$ derivável em $x=x_{0}$ é contínua neste ponto. De fato, lembramos que $f$ é contínua em $x=x_{0}$ quando $x_{0}$ é um ponto de seu domínio e

\lim_{x\to x_{0}}f(x)=f(x_{0}).

(2.95)

Isto é equivalente a

\lim_{h\to 0}f(x_{0}+h)=f(x_{0})

(2.96)

ou, ainda,

\lim_{h\to 0}\left[f(x_{0}+h)-f(x_{0})\right]=0.

(2.97)

Vamos mostrar que este é o caso quando $f$ é derivável em $x=x_{0}$ . Neste caso, temos

	$\displaystyle\lim_{h\to 0}\left[f(x_{0}+h)-f(x_{0})\right]=\lim_{h\to 0}\left[% f(x_{0}+h)-f(x_{0})\right]\cdot\frac{h}{h}$		(2.98)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\left[\cancelto{f^{\prime}(x_{0})}{% \frac{f(x_{0}+h)-f(x_{0})}{h}}\right]\cdot h$		(2.99)
	$\displaystyle\text{}\quad=\lim_{h\to 0}f^{\prime}(x_{0})\cdot h$		(2.100)
	$\displaystyle\text{}\quad=0.$		(2.101)

Ou seja, de fato, se $f$ é derivável em $x=x_{0}$ , então $f$ é contínua em $x=x_{0}$ .

Observação 2.2.2.

2.2.2 Derivadas de ordens mais altas

f^{\prime\prime}(x):=(f^{\prime}(x))^{\prime}\leavevmode\nobreak\ \text{ou}% \leavevmode\nobreak\ \frac{\mathrm{d}^{2}}{\mathrm{d}x^{2}}f(x)=\frac{\mathrm{% d}}{\mathrm{d}x}\left(\frac{\mathrm{d}}{\mathrm{d}x}f(x)\right).

(2.102)

Exemplo 2.2.4.

Seja $f(x)=x^{3}$ . Então, a primeira derivada de $f$ é

	$\displaystyle f^{\prime}(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$		(2.103)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{(x+h)^{3}-x^{3}}{h}$		(2.104)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{x^{3}+3x^{2}h+3xh^{2}+h^{3}-x^{3}% }{h}$		(2.105)
	$\displaystyle\text{}\quad=\lim_{h\to 0}3x^{2}+\cancelto{0}{3xh}+\cancelto{0}{h% ^{2}}=3x^{2}.$		(2.106)

De posse da primeira derivada $f^{\prime}(x)=3x^{2}$ , podemos calcular a segunda derivada de $f$ , como segue:

	$\displaystyle f^{\prime\prime}(x)=[f^{\prime}(x)]^{\prime}$		(2.107)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{f^{\prime}(x+h)-f^{\prime}(x)}{h}$		(2.108)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{3(x+h)^{2}-3x^{2}}{h}$		(2.109)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{3x^{2}+6xh+h^{2}-3x^{2}}{h}$		(2.110)
	$\displaystyle\text{}\quad=\lim_{h\to 0}6x+\cancelto{0}{h}=6x,$		(2.111)

i.e. $f^{\prime\prime}(x)=6x$ .

No SymPy, podemos computar a segunda derivada da função com o comando:

⬇

1 In : from sympy import *

2 ...: x = symbols('x')

3 ...: diff(x**3,x,2)

4 Out: 6*x

Generalizando, quando existe, a $n$ -ésima derivada de uma função $y=f(x)$ , $n\geq 1$ , é recursivamente definida (e denotada) por

f^{(n)}(x):=[f^{(n-1)}]^{\prime}\leavevmode\nobreak\ \text{ou}\leavevmode% \nobreak\ \frac{\mathrm{d}^{n}}{\mathrm{d}x^{n}}f(x):=\frac{\mathrm{d}}{% \mathrm{d}x}\left[\frac{\mathrm{d}^{n-1}}{\mathrm{d}x^{n-1}}f(x)\right],

(2.112)

com $f^{(3)}\equiv f^{\prime\prime\prime}$ , $f^{(2)}\equiv f^{\prime\prime}$ , $f^{(1)}\equiv f^{\prime}$ e $f^{(0)}\equiv f$ .

Exemplo 2.2.5.

A terceira derivada de $f(x)=x^{3}$ em relação a $x$ é $f^{\prime\prime\prime}(x)=[f^{\prime\prime}(x)]^{\prime}$ . No exemplo anterior (Exemplo 2.2.4), calculamos $f^{\prime\prime}(x)=6x$ . Logo,

	$\displaystyle f^{\prime\prime\prime}(x)=[6x]^{\prime}$		(2.113)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{6(x+h)-6x}{h}$		(2.114)
	$\displaystyle\text{}\quad=\lim_{h\to 0}6=6.$		(2.115)

A quarta derivada de $f(x)=x^{3}$ em relação a $x$ é $f^{(4)}(x)\equiv 0$ , bem como $f^{(5)}(x)\equiv 0$ . Verifique!

No SymPy, podemos computar a terceira derivada da função com o comando:

⬇

1 In : from sympy import *

2 ...: x = symbols('x')

3 ...: diff(x**3,x,3)

4 Out: 6

2.2.3 Exercícios resolvidos

ER 2.2.1.

Calcule a derivada da função $f(x)=x^{2}+2x+1$ em relação a $x$ .

Solução 0.

Por definição da derivada, temos

	$\displaystyle f^{\prime}(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$		(2.116)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{(x+h)^{2}+2(x+h)+1-(x^{2}+2x+1)}{h}$		(2.117)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{x^{2}+2xh+h^{2}+2x+2h+1-x^{2}-2x-% 1}{h}$		(2.118)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{2xh+h^{2}+2h}{h}$		(2.119)
	$\displaystyle\text{}\quad=\lim_{h\to 0}2x+h+2=2x+2.$		(2.120)

ER 2.2.2.

Determine os pontos de diferenciabilidade da função $f(x)=|x-1|$ .

Solução 0.

O gráfico da função $f(x)=|x-1|$ tem um bico no ponto $x=1$ (verifique!). Para valores de $x<1$ , temos

	$\displaystyle f^{\prime}(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$		(2.121)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{\|\overbrace{x+h-1}^{<0}\|-\|% \overbrace{x-1}^{<0}\|}{h}$		(2.122)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{-x-h+1+x-1}{h}$		(2.123)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{-h}{h}=-1.$		(2.124)

Para valores de $x>1$ , temos

	$\displaystyle f^{\prime}(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$		(2.125)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{\|\overbrace{x+h-1}^{>0}\|-\|% \overbrace{x-1}^{>0}\|}{h}$		(2.126)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{x+h-1-x+1}{h}$		(2.127)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{h}{h}=1.$		(2.128)

Ou seja, temos que $f(x)=|x-1|$ é diferenciável para $x\neq 1$ . Agora, para $x=1$ , temos

$\displaystyle f^{\prime}_{-}(x)=\lim_{h\to 0^{-}}\frac{f(1+h)-f(1)}{h}$		(2.129)
$\displaystyle\text{}\quad=\lim_{h\to 0^{-}}\frac{\|\overbrace{h}^{<0}\|-\|1-1\|}{h}$		(2.130)
$\displaystyle\text{}\quad=\lim_{h\to 0^{-}}\frac{-h}{h}=-1$		(2.131)
$\displaystyle f^{\prime}_{+}(x)$	$\displaystyle=\lim_{h\to 0^{+}}\frac{f(1+h)-f(1)}{h}$	(2.132)
$\displaystyle\text{}\quad=\lim_{h\to 0^{+}}\frac{\|\overbrace{h}^{>0}\|-\|1-1\|}{h}$		(2.133)
$\displaystyle\text{}\quad=\lim_{h\to 0^{+}}\frac{h}{h}=1$		(2.134)

Como $f^{\prime}_{-}(1)\neq f^{\prime}_{+}(1)$ , temos que $\nexists f^{\prime}(1)$ . Concluímos que $f(x)=|x-1|$ é diferenciável nos pontos $\mathbb{R}\setminus\{1\}$ .

ER 2.2.3.

Calcule a segunda derivada em relação a $x$ da função

f(x)=x-x^{2}.

(2.136)

Solução 0.

Começamos calculando a primeira derivada da função:

	$\displaystyle f^{\prime}(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$		(2.137)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{(x+h)-(x+h)^{2}-(x-x^{2})}{h}$		(2.138)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{x+h-x^{2}-2xh-h^{2}-x+x^{2}}{h}$		(2.139)
	$\displaystyle\text{}\quad=\lim_{h\to 0}1-2x-\cancelto{0}{h}=1-2x.$		(2.140)

Então, calculamos a segunda derivada como segue

	$\displaystyle f^{\prime\prime}(x)=[f^{\prime}(x)]^{\prime}$		(2.141)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{f^{\prime}(x+h)-f^{\prime}(x)}{h}$		(2.142)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{1-2(x+h)-(1-2x)}{h}$		(2.143)
	$\displaystyle\text{}\quad=\lim_{h\to 0}-2=-2.$		(2.144)

2.2.4 Exercícios

E. 2.2.1.

Calcule a derivada em relação a $x$ de cada uma das seguintes funções:

a)

$f(x)=2$
b)

$g(x)=-3$
c)

$h(x)=\sqrt{e}$

Resposta 0.

a) $0$ ; b) $0$ ; c) $0$

E. 2.2.2.

Calcule a derivada em relação a $x$ de cada uma das seguintes funções:

a)

$f(x)=2x$
b)

$g(x)=-3x$
c)

$h(x)=\sqrt{e}x$

Resposta 0.

a) $2$ ; b) $-3$ ; c) $\sqrt{e}$

E. 2.2.3.

Calcule a derivada em relação a $x$ da função

f(x)=x^{2}-2x+1.

(2.145)

Resposta 0.

$f^{\prime}(x)=2x-2$

E. 2.2.4.

Determine os pontos de diferenciabilidade da função $f(x)=\sqrt{x-1}$ .

Resposta 0.

$(1,\infty)$

E. 2.2.5.

Considerando

f(x)=x^{2}-x^{3},

(2.146)

calcule:

a)

$f^{\prime}(x)$
b)

$f^{\prime\prime}(x)$
c)

$f^{\prime\prime\prime}(x)$
d)

$f^{(4)}$
e)

$f^{(1001)}(x)$

Resposta 0.

a) $2x-3x^{2}$ ; b) $2-6x$ ; c) $-6$ ; d) $0$ ; e) $0$

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Pedro H A Konzen

| | | |