Política de uso de dados

Ao navegar por este site, você concorda com a política de uso de dados.

Política de uso de dados

Ao navegar por este site, você concorda com a política de uso de dados.

| | | |

Cálculo I

2 Derivadas 2.7 Regra da cadeia 2.9 Derivação implícita

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

2.8 Diferenciabilidade da função inversa

Seja $f$ uma função diferenciável e injetora em um intervalo aberto $I$ . Então, pode-se mostrar que sua inversa $f^{-1}$ é diferenciável em qualquer ponto da imagem da $f$ no qual $f^{\prime}(f^{-1}(x))\neq 0$ e sua derivada é

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\frac{d}{dx}[f% ^{-1}(x)]=\frac{1}{f^{\prime}(f^{-1}(x))}}.

(2.456)

Exemplo 2.8.1.

Seja $f(x)=(2x-1)^{2}$ para $x>1/2$ . Para calcular sua inversa, fazemos

	$\displaystyle y=(2x-1)^{2}$		(2.457)
	$\displaystyle\sqrt{y}=2x-1$		(2.458)
	$\displaystyle x=\frac{\sqrt{y}+1}{2}$		(2.459)

Ou seja,

f^{-1}(x)=\frac{1}{2}(\sqrt{x}+1).

(2.460)

Calculando a derivada de $f^{-1}$ diretamente, temos

	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}f^{-1}(x)=\frac{1}{2}\left(\sqrt{x}% +1\right)^{\prime}$		(2.461)
	$\displaystyle\text{}\quad=\frac{1}{2}\cdot\frac{1}{2\sqrt{x}}$		(2.462)
	$\displaystyle\text{}\quad=\frac{1}{4\sqrt{x}}$		(2.463)

Agora, usando (2.456) e observando que $f^{\prime}(x)=8x-4$ , obtemos

	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}f^{-1}(x)=\frac{1}{f^{\prime}(f^{-1% }(x))},$		(2.464)
	$\displaystyle\text{}\quad=\frac{1}{8\cdot\frac{1}{2}\left(\sqrt{x}+1\right)-4},$		(2.465)
	$\displaystyle\text{}\quad=\frac{1}{4\sqrt{x}},$		(2.466)

como esperado.

Observação 2.8.1.

(Derivada da função logarítmica)

•

Tomando $f(x)=e^{x}$ temos $f^{-1}(x)=\ln x$ e, daí por (2.456)

$\frac{\mathrm{d}}{\mathrm{d}x}\ln x=\frac{1}{e^{\ln x}}=\frac{1}{x}.$ (2.467)
•

Tomando $f(x)=a^{x}$ , $a>0$ e $a\neq 1$ , temos $f^{-1}(x)=\log_{a}x$ e, por (2.456),

$\frac{\mathrm{d}}{\mathrm{d}x}\log_{a}x=\frac{1}{a^{\log_{a}x}\ln a}=\frac{1}{% x\ln a}.$ (2.468)

Exemplo 2.8.2.

Vamos calcular a derivada em relação a $x$ da função

f(x)=\ln\frac{1}{x}.

(2.469)

Aplicando a regra da cadeia na derivada da função logarítmica, temos

\frac{\mathrm{d}}{\mathrm{d}x}\ln u=\frac{1}{u}\frac{\mathrm{d}u}{\mathrm{d}x}.

(2.470)

Portanto, temos

	$\displaystyle f^{\prime}(x)=\left(\ln\frac{1}{x}\right)^{\prime}$		(2.471)
	$\displaystyle\text{}\quad=\frac{1}{x^{-1}}\cdot(-x^{-2})$		(2.472)
	$\displaystyle\text{}\quad=-\frac{1}{x}.$		(2.473)

No SymPy, temos:

⬇

1 from sympy import *

2 x = Symbol('x')

3 diff(log(1/x),x)

4 -1/x

2.8.1 Derivadas de funções trigonométricas inversas

Seja $f(x)=\operatorname{sen}x$ restrita a $-\pi/2\leq x\leq\pi/2$ . Sua inversa é a função arco seno, denotada por

y=\operatorname{arc}\operatorname{sen}x.

(2.474)

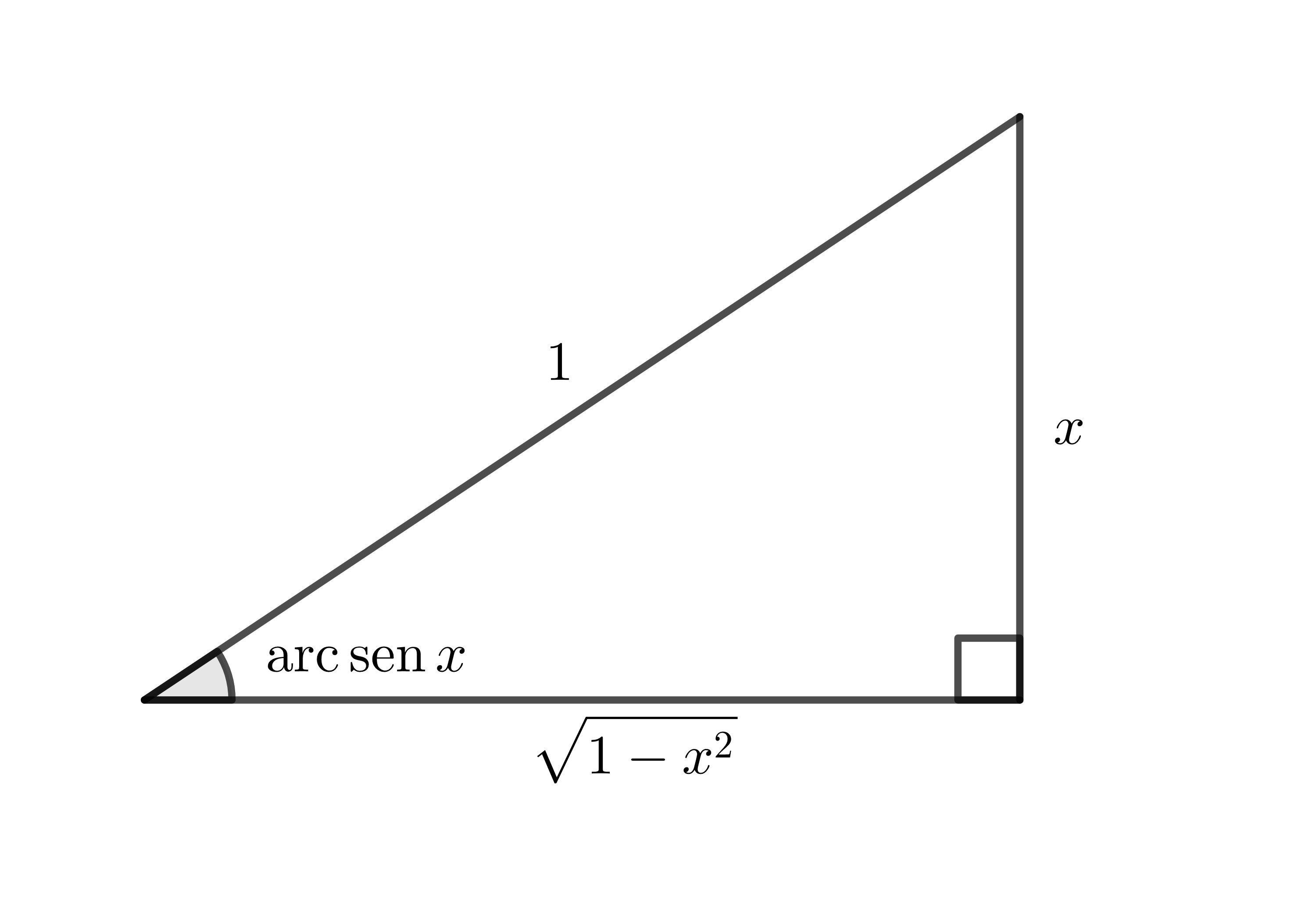
Refer to caption — Figura 2.9: Arco seno de um ângulo no triângulo retângulo.

Para calcular a derivada da função arco seno, vamos usar (2.456) com $f(x)=\operatorname{sen}x$ e $f^{\prime}(x)=\operatorname{arc}\operatorname{sen}x$ , donde

(\operatorname{arc}\operatorname{sen}x)^{\prime}=\frac{1}{\cos(\operatorname{% arc}\operatorname{sen}x)}.

(2.475)

Como $\cos(\operatorname{arc}\operatorname{sen}x)=\sqrt{1-x^{2}}$ (veja Figura 2.9), concluímos

(\operatorname{arc}\operatorname{sen}x)^{\prime}=\frac{1}{\sqrt{1-x^{2}}}.

(2.476)

Exemplo 2.8.3.

A regra da cadeia aplicada à derivada da função arco seno é

\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{arc}\operatorname{sen}u=\frac{1}{% \sqrt{1-u^{2}}}\frac{\mathrm{d}u}{\mathrm{d}x}.

(2.477)

Por exemplo, temos

\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{arc}\operatorname{sen}x^{2}=\frac{% 2x}{\sqrt{1-x^{4}}}.

(2.478)

No SymPy, temos:

⬇

1 from sympy import *

2 x = Symbol('x')

3 diff(asin(x**2),x)

4 2*x/sqrt(-x**4 + 1)

Com argumentos análogos aos usados no cálculo da derivada da função arco seno, podemos obter as seguintes derivadas:

	$\displaystyle(\operatorname{arc}\cos x)^{\prime}=-\frac{1}{\sqrt{1-x^{2}}}$		(2.479)
	$\displaystyle(\operatorname{arc}\operatorname{tg}x)^{\prime}=\frac{1}{1+x^{2}}$		(2.480)
	$\displaystyle(\operatorname{arc}\operatorname{cotg}x)^{\prime}=-\frac{1}{1+x^{% 2}}$		(2.481)
	$\displaystyle(\operatorname{arc}\sec x)^{\prime}=\frac{1}{\|x\|\sqrt{x^{2}-1}}$		(2.482)
	$\displaystyle(\operatorname{arc}\operatorname{cosec}x)^{\prime}=-\frac{1}{\|x\|% \sqrt{x^{2}-1}}$		(2.483)

Exemplo 2.8.4.

A regra da cadeia aplicada a função arco tangente é

\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{arc}\operatorname{tg}u=\frac{1}{1+% u^{2}}\frac{\mathrm{d}u}{\mathrm{d}x}.

(2.484)

Por exemplo, temos

	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{arc}\operatorname{tg}% \sqrt{x}=\frac{1}{1+(\sqrt{x})^{2}}\frac{\mathrm{d}}{\mathrm{d}x}\sqrt{x}$		(2.485)
	$\displaystyle\text{}\quad=\frac{1}{2(1+x)\sqrt{x}}.$		(2.486)

No SymPy, temos:

⬇

1 from sympy import *

2 x = Symbol('x')

3 diff(atan(sqrt(x)))

4 1/(2*sqrt(x)*(x + 1))

2.8.2 Lista de derivadas

	$\displaystyle(ku)^{\prime}=ku^{\prime}$		(2.487)
	$\displaystyle(u\pm v)^{\prime}=u^{\prime}\pm v^{\prime}$		(2.488)
	$\displaystyle(uv)^{\prime}=u^{\prime}v+uv^{\prime}$		(2.489)
	$\displaystyle\left(\frac{u}{v}\right)^{\prime}=\frac{u^{\prime}v-uv^{\prime}}{% v^{2}}$		(2.490)
	$\displaystyle(k)^{\prime}=0$		(2.491)
	$\displaystyle(x)^{\prime}=1$		(2.492)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}u^{r}=ru^{r-1}\frac{\mathrm{d}u}{% \mathrm{d}x}$		(2.493)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}a^{u}=a^{u}\ln a\frac{\mathrm{d}u}{% \mathrm{d}x}$		(2.494)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}e^{u}=e^{u}\frac{\mathrm{d}u}{% \mathrm{d}x}$		(2.495)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\log_{a}u=\frac{1}{u\ln a}\frac{% \mathrm{d}u}{\mathrm{d}x}$		(2.496)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\ln u=\frac{1}{u}\frac{\mathrm{d}u}% {\mathrm{d}x}$		(2.497)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{sen}u=\cos(u)\frac{% \mathrm{d}u}{\mathrm{d}x}$		(2.498)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\cos u=-\operatorname{sen}(u)\frac{% \mathrm{d}u}{\mathrm{d}x}$		(2.499)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{tg}u=\sec^{2}(u)\frac% {\mathrm{d}u}{\mathrm{d}x}$		(2.500)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{cotg}u=-\operatorname% {cossec}^{2}(u)\frac{\mathrm{d}u}{\mathrm{d}x}$		(2.501)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\sec u=\sec(u)\operatorname{tg}(u)% \frac{\mathrm{d}u}{\mathrm{d}x}$		(2.502)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{cossec}u=-% \operatorname{cossec}(u)\operatorname{cotg}(u)\frac{\mathrm{d}u}{\mathrm{d}x}$		(2.503)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{arc}\operatorname{sen% }u=\frac{1}{\sqrt{1-u^{2}}}\frac{\mathrm{d}u}{\mathrm{d}x}$		(2.504)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{arc}\cos u=-\frac{1}{% \sqrt{1-u^{2}}}\frac{\mathrm{d}u}{\mathrm{d}x}$		(2.505)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{arc}\operatorname{tg}% u=\frac{1}{1+u^{2}}\frac{\mathrm{d}u}{\mathrm{d}x}$		(2.506)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{arc}\operatorname{% cotg}u=-\frac{1}{1+u^{2}}\frac{\mathrm{d}u}{\mathrm{d}x}$		(2.507)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{arc}\sec u=\frac{1}{\|% u\|\sqrt{u^{2}-1}}\frac{\mathrm{d}u}{\mathrm{d}x}$		(2.508)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{arc}\operatorname{% cossec}u=-\frac{1}{\|u\|\sqrt{u^{2}-1}}\frac{\mathrm{d}u}{\mathrm{d}x}$		(2.509)

2.8.3 Exercícios resolvidos

ER 2.8.1.

Calcule a equação da reta tangente ao gráfico da função $f(x)=\ln x$ no ponto $x=1$ . Faça, então, um esboço dos gráficos da função e da reta tangente.

Solução.

A equação da reta tangente ao gráfico da função $f(x)=\ln x$ no ponto $x_{0}=1$ é

	$\displaystyle y=f^{\prime}(x_{0})(x-x_{0})+f(x_{0})$		(2.510)
	$\displaystyle y=f^{\prime}(1)(x-1)+f(1).$		(2.511)

Observando que

f^{\prime}(x)=(\ln x)^{\prime}=\frac{1}{x},

(2.512)

temos que a equação da reta tangente é

	$\displaystyle y=\frac{1}{1}(x-1)+\ln 1$		(2.513)
	$\displaystyle y=x-1.$		(2.514)

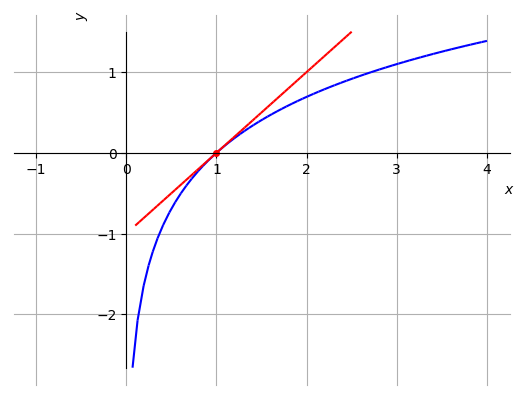
Na Figura 2.10, temos um esboço dos gráficos da função e da reta tangente.

No SymPy, temos:

⬇

1 from sympy import *

2 x = Symbol('x')

3 rt = diff(log(x)).subs(x,1)*(x-1)+log(1)

4 print("y = %s" % rt)

5 y = x - 1

ER 2.8.2.

Resolva a equação

\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{arc}\operatorname{tg}x=1.

(2.515)

Solução.

Lembrando que

\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{arc}\operatorname{tg}x=\frac{1}{1+% x^{2}},

(2.516)

temos

	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{arc}\operatorname{tg}% x=1$		(2.517)
	$\displaystyle\frac{1}{1+x^{2}}=1$		(2.518)
	$\displaystyle 1+x^{2}=1$		(2.519)
	$\displaystyle x^{2}=0$		(2.520)
	$\displaystyle x=0.$		(2.521)

ER 2.8.3.

Calcule

\frac{\mathrm{d}}{\mathrm{d}x}x^{x}.

(2.522)

Solução.

Observamos que

	$\displaystyle y=x^{x}$		(2.523)
	$\displaystyle\ln y=\ln x^{x}$		(2.524)
	$\displaystyle\ln y=x\ln x.$		(2.525)

Agora, derivando em relação a $x$ ambos os lados desta equação, obtemos

	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\ln y=\frac{\mathrm{d}}{\mathrm{d}x% }\left(x\ln x\right)$		(2.526)
	$\displaystyle\frac{1}{y}\frac{\mathrm{d}y}{\mathrm{d}x}=1+\ln x$		(2.527)
	$\displaystyle\frac{\mathrm{d}y}{\mathrm{d}x}=y(1+\ln x)$		(2.528)
	$\displaystyle\frac{\mathrm{d}x^{x}}{\mathrm{d}x}=x^{x}(1+\ln x).$		(2.529)

2.8.4 Exercícios

E. 2.8.1.

Calcule a derivada em relação a $x$ das seguintes funções:

a)

$f(x)=\log_{2}x^{2}$
b)

$g(x)=\ln(xe^{x})$

Resposta.

a) $\displaystyle f^{\prime}(x)=\frac{2}{x\ln 2}$ ; b) $g^{\prime}(x)=\frac{1+x}{x}$

E. 2.8.2.

Calcule a derivada em relação a $x$ das seguintes funções:

a)

$f(x)=\sqrt[3]{x^{2}}$
b)

$g(x)=(1+2x)^{e}$

Resposta.

a) $\displaystyle f^{\prime}(x)=\frac{2}{3\sqrt[3]{x}}$ ; b) $g^{\prime}(x)=2e(1+2x)^{e-1}$

E. 2.8.3.

Calcule

\frac{\mathrm{d}}{\mathrm{d}x}(1+x)^{x}.

(2.530)

Resposta.

$x(1+x)^{x-1}+(1+x)^{x}\ln(1+x)$

E. 2.8.4.

Encontre a equação da reta tangente ao gráfico de $f(x)=\operatorname{arc}\operatorname{tg}x$ no ponto $x=0$ .

Resposta.

$y=x$

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Cálculo I

2 Derivadas 2.7 Regra da cadeia 2.9 Derivação implícita

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

2.8 Diferenciabilidade da função inversa

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\frac{d}{dx}[f% ^{-1}(x)]=\frac{1}{f^{\prime}(f^{-1}(x))}}.

(2.456)

Exemplo 2.8.1.

Seja $f(x)=(2x-1)^{2}$ para $x>1/2$ . Para calcular sua inversa, fazemos

	$\displaystyle y=(2x-1)^{2}$		(2.457)
	$\displaystyle\sqrt{y}=2x-1$		(2.458)
	$\displaystyle x=\frac{\sqrt{y}+1}{2}$		(2.459)

Ou seja,

f^{-1}(x)=\frac{1}{2}(\sqrt{x}+1).

(2.460)

Calculando a derivada de $f^{-1}$ diretamente, temos

	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}f^{-1}(x)=\frac{1}{2}\left(\sqrt{x}% +1\right)^{\prime}$		(2.461)
	$\displaystyle\text{}\quad=\frac{1}{2}\cdot\frac{1}{2\sqrt{x}}$		(2.462)
	$\displaystyle\text{}\quad=\frac{1}{4\sqrt{x}}$		(2.463)

Agora, usando (2.456) e observando que $f^{\prime}(x)=8x-4$ , obtemos

	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}f^{-1}(x)=\frac{1}{f^{\prime}(f^{-1% }(x))},$		(2.464)
	$\displaystyle\text{}\quad=\frac{1}{8\cdot\frac{1}{2}\left(\sqrt{x}+1\right)-4},$		(2.465)
	$\displaystyle\text{}\quad=\frac{1}{4\sqrt{x}},$		(2.466)

como esperado.

Observação 2.8.1.

(Derivada da função logarítmica)

•

Tomando $f(x)=e^{x}$ temos $f^{-1}(x)=\ln x$ e, daí por (2.456)

$\frac{\mathrm{d}}{\mathrm{d}x}\ln x=\frac{1}{e^{\ln x}}=\frac{1}{x}.$ (2.467)
•

Tomando $f(x)=a^{x}$ , $a>0$ e $a\neq 1$ , temos $f^{-1}(x)=\log_{a}x$ e, por (2.456),

$\frac{\mathrm{d}}{\mathrm{d}x}\log_{a}x=\frac{1}{a^{\log_{a}x}\ln a}=\frac{1}{% x\ln a}.$ (2.468)

Exemplo 2.8.2.

Vamos calcular a derivada em relação a $x$ da função

f(x)=\ln\frac{1}{x}.

(2.469)

Aplicando a regra da cadeia na derivada da função logarítmica, temos

\frac{\mathrm{d}}{\mathrm{d}x}\ln u=\frac{1}{u}\frac{\mathrm{d}u}{\mathrm{d}x}.

(2.470)

Portanto, temos

	$\displaystyle f^{\prime}(x)=\left(\ln\frac{1}{x}\right)^{\prime}$		(2.471)
	$\displaystyle\text{}\quad=\frac{1}{x^{-1}}\cdot(-x^{-2})$		(2.472)
	$\displaystyle\text{}\quad=-\frac{1}{x}.$		(2.473)

No SymPy, temos:

⬇

1 from sympy import *

2 x = Symbol('x')

3 diff(log(1/x),x)

4 -1/x

2.8.1 Derivadas de funções trigonométricas inversas

Seja $f(x)=\operatorname{sen}x$ restrita a $-\pi/2\leq x\leq\pi/2$ . Sua inversa é a função arco seno, denotada por

y=\operatorname{arc}\operatorname{sen}x.

(2.474)

Para calcular a derivada da função arco seno, vamos usar (2.456) com $f(x)=\operatorname{sen}x$ e $f^{\prime}(x)=\operatorname{arc}\operatorname{sen}x$ , donde

(\operatorname{arc}\operatorname{sen}x)^{\prime}=\frac{1}{\cos(\operatorname{% arc}\operatorname{sen}x)}.

(2.475)

Como $\cos(\operatorname{arc}\operatorname{sen}x)=\sqrt{1-x^{2}}$ (veja Figura 2.9), concluímos

(\operatorname{arc}\operatorname{sen}x)^{\prime}=\frac{1}{\sqrt{1-x^{2}}}.

(2.476)

Exemplo 2.8.3.

A regra da cadeia aplicada à derivada da função arco seno é

\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{arc}\operatorname{sen}u=\frac{1}{% \sqrt{1-u^{2}}}\frac{\mathrm{d}u}{\mathrm{d}x}.

(2.477)

Por exemplo, temos

\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{arc}\operatorname{sen}x^{2}=\frac{% 2x}{\sqrt{1-x^{4}}}.

(2.478)

No SymPy, temos:

⬇

1 from sympy import *

2 x = Symbol('x')

3 diff(asin(x**2),x)

4 2*x/sqrt(-x**4 + 1)

Com argumentos análogos aos usados no cálculo da derivada da função arco seno, podemos obter as seguintes derivadas:

	$\displaystyle(\operatorname{arc}\cos x)^{\prime}=-\frac{1}{\sqrt{1-x^{2}}}$		(2.479)
	$\displaystyle(\operatorname{arc}\operatorname{tg}x)^{\prime}=\frac{1}{1+x^{2}}$		(2.480)
	$\displaystyle(\operatorname{arc}\operatorname{cotg}x)^{\prime}=-\frac{1}{1+x^{% 2}}$		(2.481)
	$\displaystyle(\operatorname{arc}\sec x)^{\prime}=\frac{1}{\|x\|\sqrt{x^{2}-1}}$		(2.482)
	$\displaystyle(\operatorname{arc}\operatorname{cosec}x)^{\prime}=-\frac{1}{\|x\|% \sqrt{x^{2}-1}}$		(2.483)

Exemplo 2.8.4.

A regra da cadeia aplicada a função arco tangente é

\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{arc}\operatorname{tg}u=\frac{1}{1+% u^{2}}\frac{\mathrm{d}u}{\mathrm{d}x}.

(2.484)

Por exemplo, temos

	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{arc}\operatorname{tg}% \sqrt{x}=\frac{1}{1+(\sqrt{x})^{2}}\frac{\mathrm{d}}{\mathrm{d}x}\sqrt{x}$		(2.485)
	$\displaystyle\text{}\quad=\frac{1}{2(1+x)\sqrt{x}}.$		(2.486)

No SymPy, temos:

⬇

1 from sympy import *

2 x = Symbol('x')

3 diff(atan(sqrt(x)))

4 1/(2*sqrt(x)*(x + 1))

2.8.2 Lista de derivadas

	$\displaystyle(ku)^{\prime}=ku^{\prime}$		(2.487)
	$\displaystyle(u\pm v)^{\prime}=u^{\prime}\pm v^{\prime}$		(2.488)
	$\displaystyle(uv)^{\prime}=u^{\prime}v+uv^{\prime}$		(2.489)
	$\displaystyle\left(\frac{u}{v}\right)^{\prime}=\frac{u^{\prime}v-uv^{\prime}}{% v^{2}}$		(2.490)
	$\displaystyle(k)^{\prime}=0$		(2.491)
	$\displaystyle(x)^{\prime}=1$		(2.492)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}u^{r}=ru^{r-1}\frac{\mathrm{d}u}{% \mathrm{d}x}$		(2.493)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}a^{u}=a^{u}\ln a\frac{\mathrm{d}u}{% \mathrm{d}x}$		(2.494)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}e^{u}=e^{u}\frac{\mathrm{d}u}{% \mathrm{d}x}$		(2.495)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\log_{a}u=\frac{1}{u\ln a}\frac{% \mathrm{d}u}{\mathrm{d}x}$		(2.496)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\ln u=\frac{1}{u}\frac{\mathrm{d}u}% {\mathrm{d}x}$		(2.497)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{sen}u=\cos(u)\frac{% \mathrm{d}u}{\mathrm{d}x}$		(2.498)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\cos u=-\operatorname{sen}(u)\frac{% \mathrm{d}u}{\mathrm{d}x}$		(2.499)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{tg}u=\sec^{2}(u)\frac% {\mathrm{d}u}{\mathrm{d}x}$		(2.500)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{cotg}u=-\operatorname% {cossec}^{2}(u)\frac{\mathrm{d}u}{\mathrm{d}x}$		(2.501)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\sec u=\sec(u)\operatorname{tg}(u)% \frac{\mathrm{d}u}{\mathrm{d}x}$		(2.502)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{cossec}u=-% \operatorname{cossec}(u)\operatorname{cotg}(u)\frac{\mathrm{d}u}{\mathrm{d}x}$		(2.503)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{arc}\operatorname{sen% }u=\frac{1}{\sqrt{1-u^{2}}}\frac{\mathrm{d}u}{\mathrm{d}x}$		(2.504)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{arc}\cos u=-\frac{1}{% \sqrt{1-u^{2}}}\frac{\mathrm{d}u}{\mathrm{d}x}$		(2.505)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{arc}\operatorname{tg}% u=\frac{1}{1+u^{2}}\frac{\mathrm{d}u}{\mathrm{d}x}$		(2.506)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{arc}\operatorname{% cotg}u=-\frac{1}{1+u^{2}}\frac{\mathrm{d}u}{\mathrm{d}x}$		(2.507)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{arc}\sec u=\frac{1}{\|% u\|\sqrt{u^{2}-1}}\frac{\mathrm{d}u}{\mathrm{d}x}$		(2.508)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{arc}\operatorname{% cossec}u=-\frac{1}{\|u\|\sqrt{u^{2}-1}}\frac{\mathrm{d}u}{\mathrm{d}x}$		(2.509)

2.8.3 Exercícios resolvidos

ER 2.8.1.

Calcule a equação da reta tangente ao gráfico da função $f(x)=\ln x$ no ponto $x=1$ . Faça, então, um esboço dos gráficos da função e da reta tangente.

Solução.

A equação da reta tangente ao gráfico da função $f(x)=\ln x$ no ponto $x_{0}=1$ é

	$\displaystyle y=f^{\prime}(x_{0})(x-x_{0})+f(x_{0})$		(2.510)
	$\displaystyle y=f^{\prime}(1)(x-1)+f(1).$		(2.511)

Observando que

f^{\prime}(x)=(\ln x)^{\prime}=\frac{1}{x},

(2.512)

temos que a equação da reta tangente é

	$\displaystyle y=\frac{1}{1}(x-1)+\ln 1$		(2.513)
	$\displaystyle y=x-1.$		(2.514)

Na Figura 2.10, temos um esboço dos gráficos da função e da reta tangente.

No SymPy, temos:

⬇

1 from sympy import *

2 x = Symbol('x')

3 rt = diff(log(x)).subs(x,1)*(x-1)+log(1)

4 print("y = %s" % rt)

5 y = x - 1

ER 2.8.2.

Resolva a equação

\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{arc}\operatorname{tg}x=1.

(2.515)

Solução.

Lembrando que

\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{arc}\operatorname{tg}x=\frac{1}{1+% x^{2}},

(2.516)

temos

	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\operatorname{arc}\operatorname{tg}% x=1$		(2.517)
	$\displaystyle\frac{1}{1+x^{2}}=1$		(2.518)
	$\displaystyle 1+x^{2}=1$		(2.519)
	$\displaystyle x^{2}=0$		(2.520)
	$\displaystyle x=0.$		(2.521)

ER 2.8.3.

Calcule

\frac{\mathrm{d}}{\mathrm{d}x}x^{x}.

(2.522)

Solução.

Observamos que

	$\displaystyle y=x^{x}$		(2.523)
	$\displaystyle\ln y=\ln x^{x}$		(2.524)
	$\displaystyle\ln y=x\ln x.$		(2.525)

Agora, derivando em relação a $x$ ambos os lados desta equação, obtemos

	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\ln y=\frac{\mathrm{d}}{\mathrm{d}x% }\left(x\ln x\right)$		(2.526)
	$\displaystyle\frac{1}{y}\frac{\mathrm{d}y}{\mathrm{d}x}=1+\ln x$		(2.527)
	$\displaystyle\frac{\mathrm{d}y}{\mathrm{d}x}=y(1+\ln x)$		(2.528)
	$\displaystyle\frac{\mathrm{d}x^{x}}{\mathrm{d}x}=x^{x}(1+\ln x).$		(2.529)

2.8.4 Exercícios

E. 2.8.1.

Calcule a derivada em relação a $x$ das seguintes funções:

a)

$f(x)=\log_{2}x^{2}$
b)

$g(x)=\ln(xe^{x})$

Resposta.

a) $\displaystyle f^{\prime}(x)=\frac{2}{x\ln 2}$ ; b) $g^{\prime}(x)=\frac{1+x}{x}$

E. 2.8.2.

Calcule a derivada em relação a $x$ das seguintes funções:

a)

$f(x)=\sqrt[3]{x^{2}}$
b)

$g(x)=(1+2x)^{e}$

Resposta.

a) $\displaystyle f^{\prime}(x)=\frac{2}{3\sqrt[3]{x}}$ ; b) $g^{\prime}(x)=2e(1+2x)^{e-1}$

E. 2.8.3.

Calcule

\frac{\mathrm{d}}{\mathrm{d}x}(1+x)^{x}.

(2.530)

Resposta.

$x(1+x)^{x-1}+(1+x)^{x}\ln(1+x)$

E. 2.8.4.

Encontre a equação da reta tangente ao gráfico de $f(x)=\operatorname{arc}\operatorname{tg}x$ no ponto $x=0$ .

Resposta.

$y=x$

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Pedro H A Konzen

| | | |