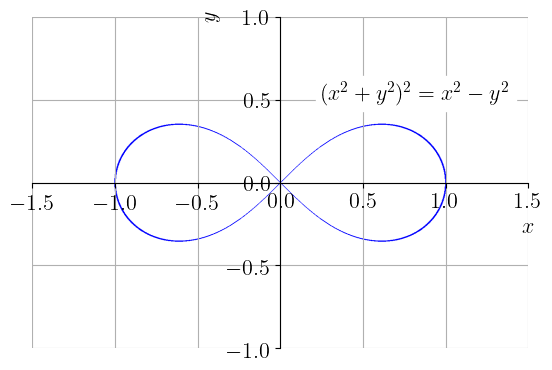Cálculo I
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
2.9 Derivação implícita
Seja definida implicitamente por
A derivada pode ser calculada via regra da cadeia
|
|
|
(2.532) |
|
|
|
(2.533) |
Exemplo 2.9.1.
Considere a equação da circunferência unitária
Aqui, vamos calcular de duas maneiras diferentes.
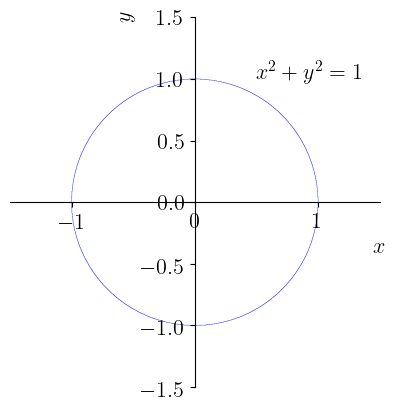 Figura 2.11: Esboço do gráfico da circunferência unitária .
Figura 2.11: Esboço do gráfico da circunferência unitária .
-
a)
Por derivação direta. Isolando em (2.534), temos
o que está bem definido para . Calculando a derivada, obtemos
|
|
|
(2.536) |
|
|
|
(2.537) |
|
|
|
(2.538) |
Ou seja, para , temos e, para , temos . Logo, concluímos que
-
b)
Por derivação implícita. Derivamos ambos os lados da (2.534) em relação a
|
|
|
(2.540) |
|
|
|
(2.541) |
|
|
|
(2.542) |
|
|
|
(2.543) |
|
|
|
(2.544) |
Observação 2.9.1.(Derivadas de potências racionais de )
Vamos mostrar que
para qualquer número racional . Denotando , , temos
|
|
|
(2.546) |
|
|
|
(2.547) |
|
|
|
(2.548) |
Da derivação de função potência com exponente inteiro, temos
|
|
|
(2.549) |
|
|
|
(2.550) |
|
|
|
(2.551) |
|
|
|
(2.552) |
|
|
|
(2.553) |
|
|
|
(2.554) |
|
|
|
(2.555) |
Logo, segue o resultados que queríamos demonstrar.
Exemplo 2.9.2.
Vamos calcular para
Primeiramente, precisamos calcular . Isso foi feito no Exemplo 2.9.1, onde obtivemos
Antes de derivarmos novamente, vamos reescrever essa última expressão da seguinte forma
Derivando
|
|
|
(2.559) |
|
|
|
(2.560) |
|
|
|
(2.561) |
|
|
|
(2.562) |
2.9.1 Exercícios resolvidos
ER 2.9.1.
Calcule para a lemniscata de Bernoulli2020endnote: 20Jacob Bernoulli, 1655 - 1705, matemático suíço. Fonte: Wikipédia.
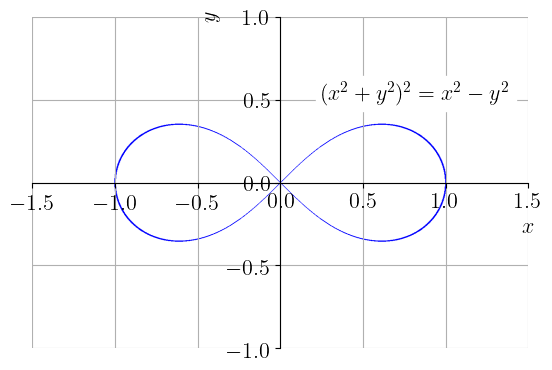 Figura 2.12: Esboço da lemniscata de Bernoulli .
Figura 2.12: Esboço da lemniscata de Bernoulli .
Solução 0.
|
|
|
(2.564) |
|
|
|
(2.565) |
Rearranjando os termos, obtemos
|
|
|
(2.566) |
ou ainda
|
|
|
(2.567) |
ER 2.9.2.
Calcule a equação da reta tangente ao gráfico da circunferência unitária
no ponto .
Solução 0.
A equação da reta tangente ao gráfico de uma função no ponto é dada por
|
|
|
(2.569) |
onde, nesse caso, ,
|
|
|
(2.570) |
Calculamos como segue
|
|
|
(2.571) |
|
|
|
(2.572) |
|
|
|
(2.573) |
|
|
|
(2.574) |
|
|
|
(2.575) |
Com isso, temos
|
|
|
(2.576) |
|
|
|
(2.577) |
|
|
|
(2.578) |
Concluímos que a equação da reta tangente é
|
|
|
(2.579) |
|
|
|
(2.580) |
2.9.2 Exercícios
E. 2.9.1.
Calcule para:
-
a)
-
b)
Resposta 0.
a) b)
E. 2.9.3.
Encontre o ponto de interseção das retas tangentes ao gráfico de
nos pontos e .
E. 2.9.4.
Encontre a equação da reta tangente ao gráfico da circunferência de centro e raio que passa pela origem .
E. 2.9.5.
Seja a circunferência de raio
Mostra que a reta tangente ao gráfico de em qualquer ponto arbitrário é perpendicular a reta , i.e. a reta que passa pela origem e pelo ponto
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.
Cálculo I
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
2.9 Derivação implícita
Seja definida implicitamente por
A derivada pode ser calculada via regra da cadeia
|
|
|
(2.532) |
|
|
|
(2.533) |
Exemplo 2.9.1.
Considere a equação da circunferência unitária
Aqui, vamos calcular de duas maneiras diferentes.
 Figura 2.11: Esboço do gráfico da circunferência unitária .
Figura 2.11: Esboço do gráfico da circunferência unitária .
-
a)
Por derivação direta. Isolando em (2.534), temos
o que está bem definido para . Calculando a derivada, obtemos
|
|
|
(2.536) |
|
|
|
(2.537) |
|
|
|
(2.538) |
Ou seja, para , temos e, para , temos . Logo, concluímos que
-
b)
Por derivação implícita. Derivamos ambos os lados da (2.534) em relação a
|
|
|
(2.540) |
|
|
|
(2.541) |
|
|
|
(2.542) |
|
|
|
(2.543) |
|
|
|
(2.544) |
Observação 2.9.1.(Derivadas de potências racionais de )
Vamos mostrar que
para qualquer número racional . Denotando , , temos
|
|
|
(2.546) |
|
|
|
(2.547) |
|
|
|
(2.548) |
Da derivação de função potência com exponente inteiro, temos
|
|
|
(2.549) |
|
|
|
(2.550) |
|
|
|
(2.551) |
|
|
|
(2.552) |
|
|
|
(2.553) |
|
|
|
(2.554) |
|
|
|
(2.555) |
Logo, segue o resultados que queríamos demonstrar.
Exemplo 2.9.2.
Vamos calcular para
Primeiramente, precisamos calcular . Isso foi feito no Exemplo 2.9.1, onde obtivemos
Antes de derivarmos novamente, vamos reescrever essa última expressão da seguinte forma
Derivando
|
|
|
(2.559) |
|
|
|
(2.560) |
|
|
|
(2.561) |
|
|
|
(2.562) |
2.9.1 Exercícios resolvidos
ER 2.9.1.
Calcule para a lemniscata de Bernoulli2020endnote: 20Jacob Bernoulli, 1655 - 1705, matemático suíço. Fonte: Wikipédia.
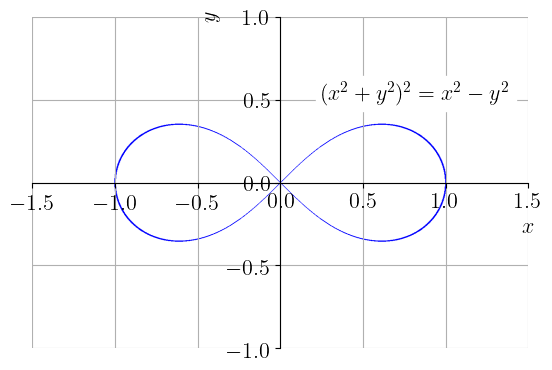 Figura 2.12: Esboço da lemniscata de Bernoulli .
Figura 2.12: Esboço da lemniscata de Bernoulli .
Solução 0.
|
|
|
(2.564) |
|
|
|
(2.565) |
Rearranjando os termos, obtemos
|
|
|
(2.566) |
ou ainda
|
|
|
(2.567) |
ER 2.9.2.
Calcule a equação da reta tangente ao gráfico da circunferência unitária
no ponto .
Solução 0.
A equação da reta tangente ao gráfico de uma função no ponto é dada por
|
|
|
(2.569) |
onde, nesse caso, ,
|
|
|
(2.570) |
Calculamos como segue
|
|
|
(2.571) |
|
|
|
(2.572) |
|
|
|
(2.573) |
|
|
|
(2.574) |
|
|
|
(2.575) |
Com isso, temos
|
|
|
(2.576) |
|
|
|
(2.577) |
|
|
|
(2.578) |
Concluímos que a equação da reta tangente é
|
|
|
(2.579) |
|
|
|
(2.580) |
2.9.2 Exercícios
E. 2.9.1.
Calcule para:
-
a)
-
b)
Resposta 0.
a) b)
E. 2.9.3.
Encontre o ponto de interseção das retas tangentes ao gráfico de
nos pontos e .
E. 2.9.4.
Encontre a equação da reta tangente ao gráfico da circunferência de centro e raio que passa pela origem .
E. 2.9.5.
Seja a circunferência de raio
Mostra que a reta tangente ao gráfico de em qualquer ponto arbitrário é perpendicular a reta , i.e. a reta que passa pela origem e pelo ponto
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.