Política de uso de dados

Ao navegar por este site, você concorda com a política de uso de dados.

Política de uso de dados

Ao navegar por este site, você concorda com a política de uso de dados.

| | | |

Cálculo I

3 Aplicações da derivada 3.2 Extremos de funções 3.4 Teste da primeira derivada

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

3.3 Teorema do valor médio

O teorema do valor médio é uma aplicação do teorema de Rolle.

3.3.1 Teorema de Rolle

O Teorema de Rolle fornece uma condição suficiente para que uma dada função diferenciável tenha derivada nula em pelo menos um ponto.

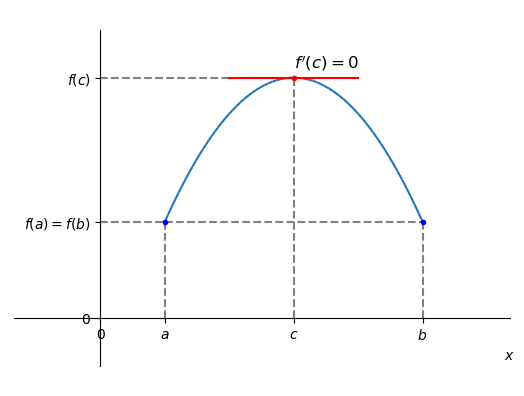
Refer to caption — Figura 3.8: Ilustração do Teorema de Rolle.

Teorema 3.3.1.

(Teorema de Rolle) Seja $f$ uma função contínua no intervalo fechado $[a,b]$ e diferenciável no intervalo aberto $(a,b)$ . Se

f(a)=f(b),

(3.51)

então existe pelo menos um ponto crítico $c\in(a,b)$ tal que

f^{\prime}(c)=0.

(3.52)

Demonstração.

A ideia da demonstração é uma consequência dos teoremas 25 e 3.2.2. O primeiro, que existem pontos de mínimo e máximos globais $m,M\in[a,b]$ , i.e.

f(m)\leq f(x)\leq f(M).

(3.53)

Se $m=M$ , então $f$ é uma função contínua, donde segue que $f^{\prime}(x)=0$ para todo $x\in(a,b)$ . Agora, se $m\neq M$ , então $m$ ou $M$ é um extremo local. Sem perda de generalidade, supomos que $c=m$ seja o mínimo local. Neste caso, o teorema 3.2.2 nos garante que $f^{\prime}(c)=0$ . ∎

Exemplo 3.3.1.

O polinômio $p(x)=x^{3}-4x^{2}+3x+1$ tem pelo menos um ponto crítico no intervalo $(0,1)$ e no intervalo $(1,3)$ . De fato,temos $p(0)=p(1)=1$ e, pelo teorema de Rolle, segue que existe pelo menos um ponto $c\in(0,1)$ tal que $f^{\prime}(c)=0$ . Analogamente, como também $p(1)=p(3)=1$ , segue do teorema que existe pelo menos um ponto crítico no intervalo $(1,3)$ . Veja o esboço do gráfico de $p$ na Figura 3.9.

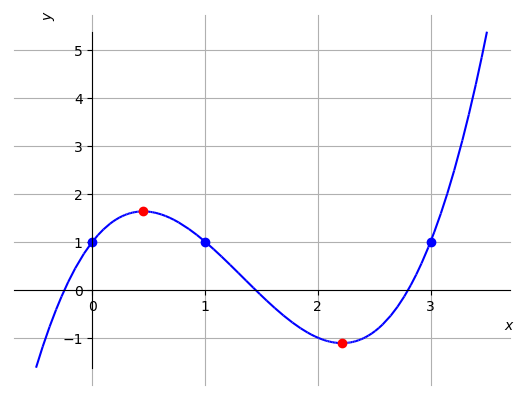
De fato, como todo polinômio é derivável em toda parte, podemos calcular os pontos críticos como segue.

$\displaystyle p^{\prime}(x)=0$	$\displaystyle\Rightarrow 3x^{2}-8x+3=0$	(3.54)
	$\displaystyle\Rightarrow x=\frac{8\pm\cancelto{2\sqrt{7}}{\sqrt{64-36}}}{6}$	(3.55)
	$\displaystyle\Rightarrow x_{1}=\frac{4-\sqrt{7}}{3}\approx 0,45\quad\text{ou}% \quad x_{2}=\frac{4+\sqrt{7}}{3}\approx 2,22.$	(3.56)

Podemos usar os seguintes comandos²⁶²⁶endnote: ²⁶Veja a Observação 3.0.1. para computar os pontos críticos de $p$ e plotar seu gráfico:

>>> p = x**3 - 4*x**2 + 3*x + 1
>>> pc = solve(p.diff()); pc
[-sqrt(7)/3 + 4/3, sqrt(7)/3 + 4/3]
>>> plot(p,(x,-0.5,3.5))

Exemplo 3.3.2.

Vejamos os seguintes casos em que o Teorema de Rolle não se aplica:

a)

A função

$f(x)=\left\{\begin{array}[]{ll}x&,0\leq x<1,\\ 0&,x=1.\end{array}\right.$ (3.57)

é tal que $f(0)=f(1)=0$ , entretanto sua derivada $f^{\prime}(x)=1$ no intervalo $(0,1)$ . Ou seja, a condição da $f$ ser contínua no intervalo fechado associado é necessária no teorema de Rolle. Veja a Figura 3.10 para o esboço do gráfico desta função.

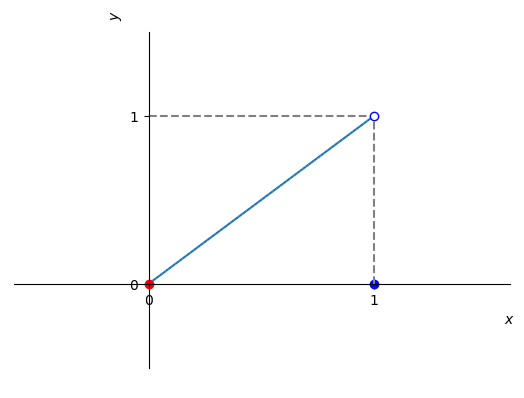
Figura 3.10: Esboço do gráfico da função referente ao Exemplo 3.3.2 a).
b)

Não existe ponto tal que a derivada da $g(x)=-|x-1|+1$ seja nula. Entretanto, notemos que $g(0)=g(2)=0$ e $g$ contínua no intervalo fechado $[0,2]$ . O teorema de Rolle não se aplica neste caso, pois $g$ não é derivável no intervalo $(0,2)$ , mais especificamente, no ponto $x=1$ . Veja a Figura 3.11.

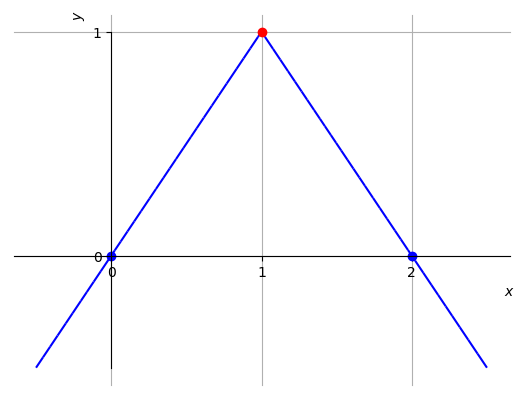
Figura 3.11: Esboço do gráfico da função referente ao Exemplo 3.3.2 b).

3.3.2 Teorema do valor médio

O teorema do valor médio é uma generalização do teorema de Rolle.

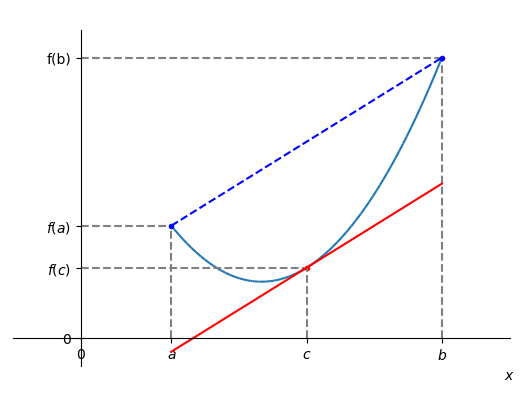
Teorema 3.3.2.

(Teorema do valor médio²⁷²⁷endnote: ²⁷Também conhecido como Teorema de Lagrange.) Seja $f$ uma função contínua no intervalo fechado $[a,b]$ e diferenciável no intervalo aberto $(a,b)$ . Então, existe pelo menos um ponto $c\in(a,b)$ tal que

\frac{f(b)-f(a)}{b-a}=f^{\prime}(c).

(3.58)

Demonstração.

O resultado segue da aplicação do Teorema de Rolle LABEL:teo:rolle a seguinte função

F(x)=f(x)-f(a)-\frac{f(b)-f(a)}{b-a}(x-a)

(3.59)

De fato, $F$ é contínua em $[a,b]$ , diferenciável em $(a,b)$ e $F(a)=F(b)$ . Logo, existe $c\in(a,b)$ tal que

	$\displaystyle F^{\prime}(c)=0$		(3.60)
	$\displaystyle f^{\prime}(c)+\frac{f(b)-f(a)}{b-a}=0$		(3.61)
	$\displaystyle\frac{f(b)-f(a)}{b-a}=f^{\prime}(c)$		(3.62)

∎

Observação 3.3.1.

Em um contexto de aplicação, o Teorema do valor médio relaciona a taxa de variação média da função em um intervalo $[a,b]$ com a taxa de variação instantânea da função em um ponto interior deste intervalo.

Exemplo 3.3.3.

A função $f(x)=x^{2}$ é contínua no intervalo $[0,2]$ e diferenciável no intervalo $(0,2)$ . Logo, segue do teorema do valor médio que existe pelo menos um ponto $c\in(0,2)$ tal que

f^{\prime}(c)=\frac{f(2)-f(0)}{2-0}=2.

(3.63)

De fato, $f^{\prime}(x)=2x$ e, portanto, tomando $c=1$ , temos $f^{\prime}(c)=2$ .

Corolário 3.3.1.

(Funções com derivadas nulas são constantes) Se $f^{\prime}(x)=0$ para todos os pontos em um intervalo $(a,b)$ , então $f$ é constante neste intervalo.

Demonstração.

De fato, sejam $x_{1},x_{2}\in(a,b)$ e, sem perda de generalidade, $x_{1}<x_{2}$ . Então, temos $f$ é contínua no intervalo $[x_{1},x_{2}]$ e diferenciável em $(x_{1},x_{2})$ . Segue do teorema do valor médio que existe $c\in(x_{1},x_{2})$ tal que

\frac{f(x_{2})-f(x_{1})}{x_{2}-x_{1}}=f^{\prime}(c).

(3.64)

Como $f^{\prime}(c)=0$ , temos $f(x_{2})=f(x_{1})$ . Ou seja, a função vale sempre o mesmo valor para quaisquer dois pontos no intervalo $(a,b)$ , logo é constante neste intervalo. ∎

Corolário 3.3.2.

(Função com a mesma derivada diferem por uma constante) Se $f^{\prime}(x)=g^{\prime}(x)$ para todos os pontos em um intervalo aberto $(a,b)$ , então $f(x)=g(x)+C$ , $C$ constante, para todo $x\in(a,b)$ .

Demonstração.

Segue, imediatamente, da aplicação do corolário anterior à função $h(x)=f(x)-g(x)$ . ∎

Corolário 3.3.3.

(Monotonicidade e o sinal da derivada) Suponha que $f$ seja contínua em $[a,b]$ e derivável em $(a,b)$ .

a)

Se $f^{\prime}(x)>0$ para todo $x\in(a,b)$ , então $f$ é crescente²⁸²⁸endnote: ²⁸ $f$ é função crescente em um intervalo $I$ , quando $x_{1}>x_{2}$ em $I$ implica $f(x_{1})>f(x_{2})$ . em $[a,b]$ .
b)

Se $f^{\prime}(x)<0$ para todo $x\in(a,b)$ , então $f$ é decrescente²⁹²⁹endnote: ²⁹ $f$ é função decrescente em um intervalo $I$ , quando $x_{1}>x_{2}$ em $I$ implica $f(x_{1})<f(x_{2})$ . em $[a,b]$ .

Demonstração.

Vamos demonstrar o item a), i.e. se $f^{\prime}(x)>0$ para todo $x\in(a,b)$ , então $f$ é crescente em $[a,b]$ . Sejam $x_{1}<x_{2}$ com $x_{1},x_{2}\in[a,b]$ . Observamos que $f$ é contínua em $[x_{1},x_{2}]$ e diferenciável em $(x_{1},x_{2})$ . Logo, pelo Teorema do valor médio 27, temos que existe $c\in(x_{1},x_{2})$ tal que

\frac{f(x_{2})-f(x_{1})}{x_{2}-x_{1}}=f^{\prime}(c)

(3.65)

ou, equivalentemente,

f(x_{2})-f(x_{1})=f^{\prime}(c)\cdot(x_{2}-x_{1}).

(3.66)

Como $f^{\prime}(x)>0$ para todo $x\in(a,b)$ e $x_{2}-x_{1}>0$ , concluímos que $f(x_{2})-f(x_{1})>0$ , i.e.

f(x_{1})<f(x_{2}).

(3.67)

Com isso, mostramos que se $x_{1}<x_{2}$ com $x_{1},x_{2}\in[a,b]$ , então $f(x_{1})<f(x_{2})$ , i.e. $f$ é crescente em $[a,b]$ .

A demonstração do item b) é análoga, consulte o Exercício 3.3.6. ∎

Exemplo 3.3.4.

Vamos estudar a monotonicidade da função polinomial $f(x)=x^{3}-4x^{2}+3x+1$ . Na Figura 3.13, temos o esboço de seu gráfico.

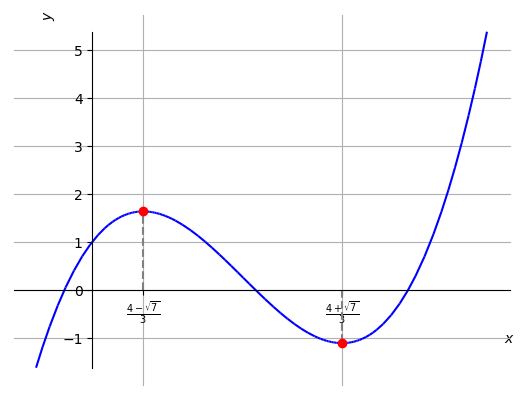
Podemos usar o Corolário 3.3.3 para estudarmos a monotonicidade (i.e. intervalos de crescimento ou decrescimento). Isto é, fazemos o estudo de sinal da derivada de $f$ . Calculamos

f^{\prime}(x)=3x^{2}-8x+3.

(3.68)

Logo, temos

Ou seja, $f^{\prime}(x)<0$ no conjunto $\displaystyle\left(-\infty,\frac{4-\sqrt{7}}{3}\right)\cup\left(\frac{4+\sqrt{% 7}}{3},\infty\right)$ e $f^{\prime}(x)<0$ no conjunto $\displaystyle\left(\frac{4-\sqrt{7}}{3},\frac{4+\sqrt{7}}{3}\right)$ . Concluímos que $f$ é crescente nos intervalos $\displaystyle\left(\left.-\infty,\frac{4-\sqrt{7}}{3}\right.\right]$ e $\displaystyle\left[\left.\frac{4+\sqrt{7}}{3},\infty\right)\right.$ , enquanto que $f$ é decrescente no intervalo $\displaystyle\left[\frac{4-\sqrt{7}}{3},\frac{4+\sqrt{7}}{3}\right]$ .

Exemplo 3.3.5.

A função exponencial $f(x)=e^{x}$ é crescente em toda parte. De fato, temos

f^{\prime}(x)=e^{x}>0,

(3.69)

para todo $x\in\mathbb{R}$ .

3.3.3 Exercícios resolvidos

ER 3.3.1.

Um carro percorreu 150 km em 1h30min. Mostre que em algum momento o carro estava a uma velocidade maior que 80 km/h.

Solução 0.

Seja $s=s(t)$ a função distância percorrida pelo carro e $t$ o tempo, em horas, contado do início do percurso. Do teorema do valor médio, exite tempo $t_{1}\in(0,\leavevmode\nobreak\ 1,5)$ tal que

f^{\prime}(t_{1})=\frac{s(1,5)-s(0)}{1,5-0}=\frac{150}{1,5}=100\leavevmode% \nobreak\ \text{km/h}.

(3.70)

Ou seja, em algum momento o carro atingiu a velocidade de 100 km/h.

ER 3.3.2.

Estude a monotonicidade da função gaussiana $f(x)=e^{-x^{2}}$ .

Solução 0.

Para estudarmos a monotonicidade de uma função, podemos fazer o estudo de sinal de sua derivada. Neste caso, temos

f^{\prime}(x)=-2xe^{-x^{2}}.

(3.71)

Assim, vemos que

Concluímos que $f$ é crescente no intervalo $(-\infty,0)$ e decrescente no intervalo $(0,\infty)$ .

3.3.4 Exercícios

E. 3.3.1.

Estude a monotonicidade de $f(x)=x^{2}-2x$ .

Resposta 0.

Decrescente: $(-\infty,1]$ ; Crescente: $[1,\infty)$

E. 3.3.2.

Estude a monotonicidade de $\displaystyle f(x)=\frac{x^{3}}{3}-x$ .

Resposta 0.

Decrescente: $[-1,1]$ ; Crescente: $(-\infty,-1]$ ; $[1,\infty)$

E. 3.3.3.

Estude a monotonicidade de $\displaystyle f(x)=\ln x$ .

Resposta 0.

Crescente: $(0,\infty)$

E. 3.3.4.

Estude a monotonicidade de $\displaystyle f(x)=xe^{-x}$ .

Resposta 0.

Crescente: $(-\infty,1)$ ; Decrescente de $(1,\infty)$

E. 3.3.5.

Demonstre que um polinômio cúbico pode ter no máximo $3$ raízes reais.

Resposta 0.

Dica: use o teorema de Rolle.

E. 3.3.6.

Seja $f$ contínua em $[a,b]$ e derivável em $(a,b)$ . Mostre que se $f^{\prime}(x)<0$ para todo $x\in(a,b)$ , então $f$ é decrescente em $[a,b]$ .

Resposta 0.

Dica: consulte a demonstração do item a) do Corolário 3.3.3.

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Cálculo I

3 Aplicações da derivada 3.2 Extremos de funções 3.4 Teste da primeira derivada

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

3.3 Teorema do valor médio

O teorema do valor médio é uma aplicação do teorema de Rolle.

3.3.1 Teorema de Rolle

O Teorema de Rolle fornece uma condição suficiente para que uma dada função diferenciável tenha derivada nula em pelo menos um ponto.

Teorema 3.3.1.

(Teorema de Rolle) Seja $f$ uma função contínua no intervalo fechado $[a,b]$ e diferenciável no intervalo aberto $(a,b)$ . Se

f(a)=f(b),

(3.51)

então existe pelo menos um ponto crítico $c\in(a,b)$ tal que

f^{\prime}(c)=0.

(3.52)

Demonstração.

A ideia da demonstração é uma consequência dos teoremas 25 e 3.2.2. O primeiro, que existem pontos de mínimo e máximos globais $m,M\in[a,b]$ , i.e.

f(m)\leq f(x)\leq f(M).

(3.53)

Exemplo 3.3.1.

De fato, como todo polinômio é derivável em toda parte, podemos calcular os pontos críticos como segue.

$\displaystyle p^{\prime}(x)=0$	$\displaystyle\Rightarrow 3x^{2}-8x+3=0$	(3.54)
	$\displaystyle\Rightarrow x=\frac{8\pm\cancelto{2\sqrt{7}}{\sqrt{64-36}}}{6}$	(3.55)
	$\displaystyle\Rightarrow x_{1}=\frac{4-\sqrt{7}}{3}\approx 0,45\quad\text{ou}% \quad x_{2}=\frac{4+\sqrt{7}}{3}\approx 2,22.$	(3.56)

Podemos usar os seguintes comandos²⁶²⁶endnote: ²⁶Veja a Observação 3.0.1. para computar os pontos críticos de $p$ e plotar seu gráfico:

>>> p = x**3 - 4*x**2 + 3*x + 1
>>> pc = solve(p.diff()); pc
[-sqrt(7)/3 + 4/3, sqrt(7)/3 + 4/3]
>>> plot(p,(x,-0.5,3.5))

Exemplo 3.3.2.

Vejamos os seguintes casos em que o Teorema de Rolle não se aplica:

a)

A função

$f(x)=\left\{\begin{array}[]{ll}x&,0\leq x<1,\\ 0&,x=1.\end{array}\right.$ (3.57)

é tal que $f(0)=f(1)=0$ , entretanto sua derivada $f^{\prime}(x)=1$ no intervalo $(0,1)$ . Ou seja, a condição da $f$ ser contínua no intervalo fechado associado é necessária no teorema de Rolle. Veja a Figura 3.10 para o esboço do gráfico desta função.

Figura 3.10: Esboço do gráfico da função referente ao Exemplo 3.3.2 a).
b)

Não existe ponto tal que a derivada da $g(x)=-|x-1|+1$ seja nula. Entretanto, notemos que $g(0)=g(2)=0$ e $g$ contínua no intervalo fechado $[0,2]$ . O teorema de Rolle não se aplica neste caso, pois $g$ não é derivável no intervalo $(0,2)$ , mais especificamente, no ponto $x=1$ . Veja a Figura 3.11.

Figura 3.11: Esboço do gráfico da função referente ao Exemplo 3.3.2 b).

3.3.2 Teorema do valor médio

O teorema do valor médio é uma generalização do teorema de Rolle.

Teorema 3.3.2.

\frac{f(b)-f(a)}{b-a}=f^{\prime}(c).

(3.58)

Demonstração.

O resultado segue da aplicação do Teorema de Rolle LABEL:teo:rolle a seguinte função

F(x)=f(x)-f(a)-\frac{f(b)-f(a)}{b-a}(x-a)

(3.59)

De fato, $F$ é contínua em $[a,b]$ , diferenciável em $(a,b)$ e $F(a)=F(b)$ . Logo, existe $c\in(a,b)$ tal que

	$\displaystyle F^{\prime}(c)=0$		(3.60)
	$\displaystyle f^{\prime}(c)+\frac{f(b)-f(a)}{b-a}=0$		(3.61)
	$\displaystyle\frac{f(b)-f(a)}{b-a}=f^{\prime}(c)$		(3.62)

∎

Observação 3.3.1.

Exemplo 3.3.3.

A função $f(x)=x^{2}$ é contínua no intervalo $[0,2]$ e diferenciável no intervalo $(0,2)$ . Logo, segue do teorema do valor médio que existe pelo menos um ponto $c\in(0,2)$ tal que

f^{\prime}(c)=\frac{f(2)-f(0)}{2-0}=2.

(3.63)

De fato, $f^{\prime}(x)=2x$ e, portanto, tomando $c=1$ , temos $f^{\prime}(c)=2$ .

Corolário 3.3.1.

(Funções com derivadas nulas são constantes) Se $f^{\prime}(x)=0$ para todos os pontos em um intervalo $(a,b)$ , então $f$ é constante neste intervalo.

Demonstração.

\frac{f(x_{2})-f(x_{1})}{x_{2}-x_{1}}=f^{\prime}(c).

(3.64)

Como $f^{\prime}(c)=0$ , temos $f(x_{2})=f(x_{1})$ . Ou seja, a função vale sempre o mesmo valor para quaisquer dois pontos no intervalo $(a,b)$ , logo é constante neste intervalo. ∎

Corolário 3.3.2.

Demonstração.

Segue, imediatamente, da aplicação do corolário anterior à função $h(x)=f(x)-g(x)$ . ∎

Corolário 3.3.3.

(Monotonicidade e o sinal da derivada) Suponha que $f$ seja contínua em $[a,b]$ e derivável em $(a,b)$ .

a)

Se $f^{\prime}(x)>0$ para todo $x\in(a,b)$ , então $f$ é crescente²⁸²⁸endnote: ²⁸ $f$ é função crescente em um intervalo $I$ , quando $x_{1}>x_{2}$ em $I$ implica $f(x_{1})>f(x_{2})$ . em $[a,b]$ .
b)

Se $f^{\prime}(x)<0$ para todo $x\in(a,b)$ , então $f$ é decrescente²⁹²⁹endnote: ²⁹ $f$ é função decrescente em um intervalo $I$ , quando $x_{1}>x_{2}$ em $I$ implica $f(x_{1})<f(x_{2})$ . em $[a,b]$ .

Demonstração.

\frac{f(x_{2})-f(x_{1})}{x_{2}-x_{1}}=f^{\prime}(c)

(3.65)

ou, equivalentemente,

f(x_{2})-f(x_{1})=f^{\prime}(c)\cdot(x_{2}-x_{1}).

(3.66)

Como $f^{\prime}(x)>0$ para todo $x\in(a,b)$ e $x_{2}-x_{1}>0$ , concluímos que $f(x_{2})-f(x_{1})>0$ , i.e.

f(x_{1})<f(x_{2}).

(3.67)

Com isso, mostramos que se $x_{1}<x_{2}$ com $x_{1},x_{2}\in[a,b]$ , então $f(x_{1})<f(x_{2})$ , i.e. $f$ é crescente em $[a,b]$ .

A demonstração do item b) é análoga, consulte o Exercício 3.3.6. ∎

Exemplo 3.3.4.

Vamos estudar a monotonicidade da função polinomial $f(x)=x^{3}-4x^{2}+3x+1$ . Na Figura 3.13, temos o esboço de seu gráfico.

Podemos usar o Corolário 3.3.3 para estudarmos a monotonicidade (i.e. intervalos de crescimento ou decrescimento). Isto é, fazemos o estudo de sinal da derivada de $f$ . Calculamos

f^{\prime}(x)=3x^{2}-8x+3.

(3.68)

Logo, temos

Exemplo 3.3.5.

A função exponencial $f(x)=e^{x}$ é crescente em toda parte. De fato, temos

f^{\prime}(x)=e^{x}>0,

(3.69)

para todo $x\in\mathbb{R}$ .

3.3.3 Exercícios resolvidos

ER 3.3.1.

Um carro percorreu 150 km em 1h30min. Mostre que em algum momento o carro estava a uma velocidade maior que 80 km/h.

Solução 0.

f^{\prime}(t_{1})=\frac{s(1,5)-s(0)}{1,5-0}=\frac{150}{1,5}=100\leavevmode% \nobreak\ \text{km/h}.

(3.70)

Ou seja, em algum momento o carro atingiu a velocidade de 100 km/h.

ER 3.3.2.

Estude a monotonicidade da função gaussiana $f(x)=e^{-x^{2}}$ .

Solução 0.

Para estudarmos a monotonicidade de uma função, podemos fazer o estudo de sinal de sua derivada. Neste caso, temos

f^{\prime}(x)=-2xe^{-x^{2}}.

(3.71)

Assim, vemos que

Concluímos que $f$ é crescente no intervalo $(-\infty,0)$ e decrescente no intervalo $(0,\infty)$ .

3.3.4 Exercícios

E. 3.3.1.

Estude a monotonicidade de $f(x)=x^{2}-2x$ .

Resposta 0.

Decrescente: $(-\infty,1]$ ; Crescente: $[1,\infty)$

E. 3.3.2.

Estude a monotonicidade de $\displaystyle f(x)=\frac{x^{3}}{3}-x$ .

Resposta 0.

Decrescente: $[-1,1]$ ; Crescente: $(-\infty,-1]$ ; $[1,\infty)$

E. 3.3.3.

Estude a monotonicidade de $\displaystyle f(x)=\ln x$ .

Resposta 0.

Crescente: $(0,\infty)$

E. 3.3.4.

Estude a monotonicidade de $\displaystyle f(x)=xe^{-x}$ .

Resposta 0.

Crescente: $(-\infty,1)$ ; Decrescente de $(1,\infty)$

E. 3.3.5.

Demonstre que um polinômio cúbico pode ter no máximo $3$ raízes reais.

Resposta 0.

Dica: use o teorema de Rolle.

E. 3.3.6.

Seja $f$ contínua em $[a,b]$ e derivável em $(a,b)$ . Mostre que se $f^{\prime}(x)<0$ para todo $x\in(a,b)$ , então $f$ é decrescente em $[a,b]$ .

Resposta 0.

Dica: consulte a demonstração do item a) do Corolário 3.3.3.

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Pedro H A Konzen

| | | |