Vetores

1 Fundamentos 1.2 Definição de vetor 2 Bases e coordenadas

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

1.3 Operações elementares com vetores

Vamos introduzir operações vetoriais de adição e multiplicação por escalar.

1.3.1 Adição de vetores

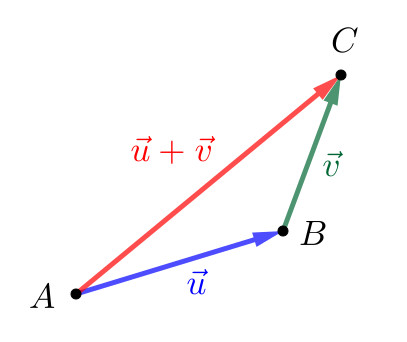
Sejam dados dois vetores $\vec{u}$ e $\vec{v}$ . Sejam, ainda, suas representações $\vec{u}=\overrightarrow{AB}$ e $\vec{v}=\overrightarrow{BC}$ . Então, definimos o vetor soma $\vec{u}+\vec{v}$ como o vetor que admite a representação $\vec{u}+\vec{v}=\overrightarrow{AC}$ . Consulte a Figura 1.17.

Refer to caption — Figura 1.17: Vetor soma resultante da adição entre dois vetores.

Propriedades

A operação de adição tem as seguintes propriedades notáveis.

•

Elemento neutro da adição

$\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\vec{u}+\vec{% 0}=\vec{u}.$ (1.8)

De fato, seja a representação do vetor $\vec{u}=\overrightarrow{AB}$ . Observamos que podemos representar $\vec{0}=\overrightarrow{BB}$ . Por definição da adição de vetores, temos

$\displaystyle\vec{u}+\vec{0}$ $\displaystyle=\overrightarrow{AB}+\overrightarrow{BB}$ (1.9)

$\displaystyle=\overrightarrow{AB}=\vec{u}.$ (1.10)
•

Associatividade da adição

$\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}(\vec{u}+\vec% {v})+\vec{w}=\vec{u}+(\vec{v}+\vec{w}).$ (1.11)

De fato, sejam as representações $\vec{u}=\overrightarrow{AB}$ , $\vec{v}=\overrightarrow{BC}$ e $\vec{w}=\overrightarrow{CD}$ . Então, segue

$\displaystyle\left(\vec{u}+\vec{v}\right)+\vec{w}$ $\displaystyle=\left(\overrightarrow{AB}+\overrightarrow{BC}\right)+% \overrightarrow{CD}$ (1.12)

$\displaystyle=\overrightarrow{AC}+\overrightarrow{CD}$ (1.13)

$\displaystyle=\overrightarrow{AD},$ (1.14)

bem como,

$\displaystyle\vec{u}+\left(\vec{v}+\vec{w}\right)$ $\displaystyle=\overrightarrow{AB}+\left(\overrightarrow{BC}+\overrightarrow{CD% }\right)$ (1.15)

$\displaystyle=\overrightarrow{AB}+\overrightarrow{BD}$ (1.16)

$\displaystyle=\overrightarrow{AD}.$ (1.17)
•

Comutatividade da adição

$\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\vec{u}+\vec{% v}=\vec{v}+\vec{u}.$ (1.18)

Para vetores $\vec{u}$ e $\vec{v}$ de mesma direção, a comutatividade de adição é direta. Noutro caso, podemos usar a regra do paralelogramo, que introduziremos logo mais. Consulte, também, o exercício resolvido ER.1.3.2.

1.3.2 Vetor oposto

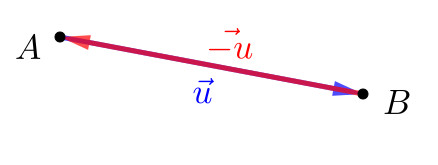
Definimos o vetor oposto a $\vec{u}$ , pelo vetor $-\vec{u}$ que tem o mesmo comprimento e a mesma direção de $\vec{u}$ , mas tem sentido oposto a $\vec{u}$ . Consulte a Figura 1.18.

Observação 1.3.1.

(Oposto do Vetor Nulo.) Por completude, definimos $-\vec{0}=\vec{0}$ .

Propriedade

•

Elemento oposto da adição

$\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\vec{u}+(-% \vec{u})=\vec{0}.$ (1.19)

Dado um vetor e sua representação $\vec{u}=\overrightarrow{AB}$ . Por definição, $-\vec{u}=\overrightarrow{BA}$ e, então,

$\displaystyle\vec{u}+(-\vec{u})$ $\displaystyle=\overrightarrow{AB}+\overrightarrow{BA}$ (1.20)

$\displaystyle=\overrightarrow{AA}$ (1.21)

$\displaystyle=\vec{0}.$ (1.22)

Consulte a Figura 1.18.

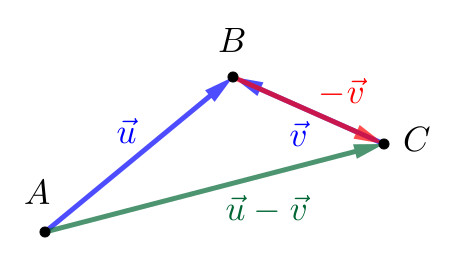
1.3.3 Subtração de vetores

A subtração do vetor $\vec{u}$ pelo vetor $\vec{v}$ é denotada por $\vec{u}-\vec{v}$ e definida por

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\vec{u}-\vec{% v}:=\vec{u}+(-\vec{v}).

(1.23)

Consultamos a Figura 1.19.

Regra do paralelogramo

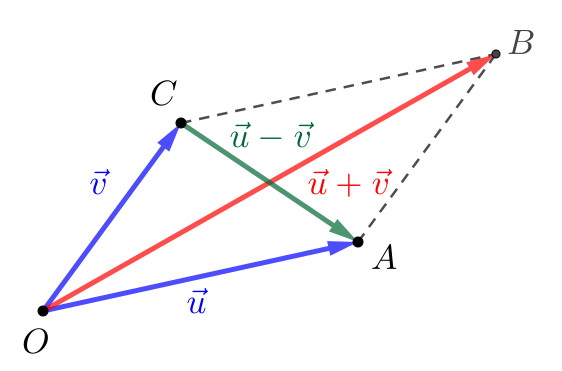
Sejam $\vec{u}=\overrightarrow{OA}$ e $\vec{v}=\overrightarrow{OC}$ vetores não nulos e de diferentes direções. Seja, então o paralelogramo $O A B C$ determinado por eles (consulte o exercício resolvido ER.1.2.2). Por observação direta, temos que $\vec{u}+\vec{v}=\overrightarrow{OB}$ e $\vec{u}-\vec{v}=\overrightarrow{CA}$ . Consulte a Figura 1.20.

1.3.4 Multiplicação de vetor por escalar

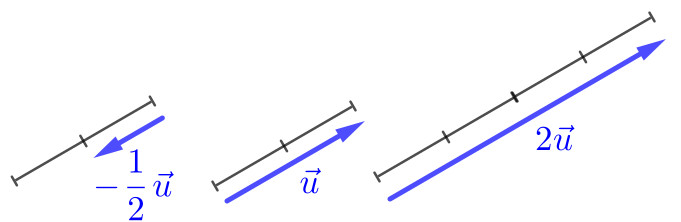
A multiplicação de um número real $\alpha>0$ (escalar) por um vetor $\vec{u}$ é denotado por $\alpha\vec{u}$ e é definido pelo vetor de mesma direção e mesmo sentido de $\vec{u}$ e com norma $\alpha\|\vec{u}\|$ . Quando $\alpha=0$ , definimos $\alpha\vec{u}=\vec{0}$ . Consulte a Figura 1.21.

Observação 1.3.2.

( $\alpha<0$ .) No caso de $\alpha<0$ , definimos

\alpha\vec{u}=-(-\alpha\vec{u}).

(1.24)

Proposição 1.3.1.

Para quaisquer número real $\alpha$ e vetor $\vec{u}$ , temos

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\|\alpha\vec{% u}\|=|\alpha|\left|\vec{u}\right|.

(1.25)

Demonstração.

$\displaystyle\\|\alpha\vec{u}\\|$	$\displaystyle=\\|-\alpha\vec{u}\\|$	(1.26)
	$\displaystyle=-\alpha\\|\vec{u}\\|$	(1.27)
	$\displaystyle=\|\alpha\|\\|\vec{u}\\|.$	(1.28)

∎

Propriedades

•

Elemento neutro da multiplicação por escalar

$\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}1\vec{u}=\vec% {u}.$ (1.29)

De fato, como $1>0$ , temos que $1\vec{u}$ e $\vec{u}$ têm a mesma direção e o mesmo sentido. Também, têm a mesma norma, pois

$\displaystyle\left\|1\vec{u}\right\|$ $\displaystyle=|1|\left\|\vec{u}\right\|$ (1.30)

$\displaystyle=\left\|\vec{u}\right\|.$ (1.31)
•

Compatibilidade da multiplicação

$\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\alpha(\beta% \vec{u})=(\alpha\beta)\vec{u}$ (1.32)

De fato, dados $\alpha,\beta$ números reais e $\vec{u}$ vetor, é direto que $\alpha(\beta\vec{u})$ e $(\alpha\beta)\vec{u}$ têm a mesma direção e o mesmo sentido. Por fim, temos

$\displaystyle\left\|\alpha(\beta\vec{u})\right\|$ $\displaystyle=\left|\alpha\right|\left\|\beta\vec{u}\right\|$ (1.33)

$\displaystyle=\left|\alpha\right|\left|\beta\right|\left\|\vec{u}\right\|$ (1.34)

$\displaystyle=\left|\alpha\beta\right|\left\|\vec{u}\right\|$ (1.35)

$\displaystyle=\left\|(\alpha\beta)\vec{u}\right\|.$ (1.36)
•

Distributividade

$\displaystyle\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% (\alpha+\beta)\vec{u}=\alpha\vec{u}+\beta\vec{u}$ (1.37)

$\displaystyle\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \alpha\left(\vec{u}+\vec{v}\right)=\alpha\vec{u}+\alpha\vec{v}$ (1.38)

A primeira, segue diretamente da noção de comprimento de segmentos orientados. A segunda, segue da semelhança de triângulos. Consulte a Figura 1.22.

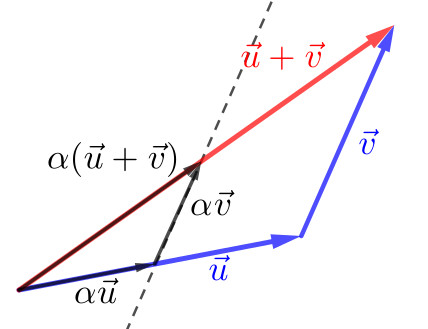
Figura 1.22: Distributividade da multiplicação vetor por escalar.

1.3.5 Resumo das propriedades

Para quaisquer vetores $\vec{u}$ , $\vec{v}$ e $\vec{w}$ e quaisquer escalares $\alpha$ e $\beta$ , valem as seguintes propriedades:

•

Associatividade da adição

$\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\vec{u}+(\vec% {v}+\vec{w})=(\vec{u}+\vec{v})+\vec{w}$ (1.39)
•

Comutatividade da adição

$\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\vec{u}+\vec{% v}=\vec{v}+\vec{u}$ (1.40)
•

Elemento neutro da adução

$\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\vec{u}+vec{0% }=\vec{u}$ (1.41)
•

Compatibilidade da multiplicação por escalar

$\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\alpha(\beta% \vec{u})=(\alpha\beta)\vec{u}$ (1.42)
•

Elemento neutro da multiplicação por escalar

$\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}1\vec{u}=\vec% {u}$ (1.43)
•

Distributividade

$\displaystyle\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% (\alpha+\beta)\vec{u}=\alpha\vec{u}+\beta\vec{u}$ (1.44)

$\displaystyle\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \alpha(\vec{u}+\vec{v})=\alpha\vec{u}+\alpha\vec{v}$ (1.45)

Exercícios resolvidos

ER 1.3.1.

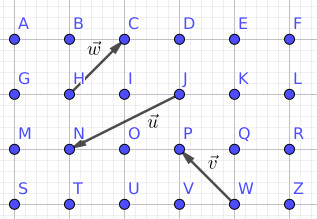
Com base na Figura 1.23, forneça o vetor $\vec{w}$ como resultado de operações básicas envolvendo os vetores $\vec{u}$ e $\vec{v}$ .

Resolução.

Vamos construir dois vetores auxiliares $\overrightarrow{HB}$ e $\overrightarrow{HI}$ a partir de operações envolvendo os vetores $\vec{u}$ e $\vec{v}$ . Notamos que $\overrightarrow{HC}=\overrightarrow{HI}+\overrightarrow{HB}$ .

Começamos buscando formar o vetor $\overrightarrow{HI}$ . Para tanto, observamos que $\vec{u}=\overrightarrow{NG}$ e, portanto, $\vec{v}+\vec{u}=\overrightarrow{JG}$ . Com isso, obtemos que

	$\displaystyle\overrightarrow{HI}$	$\displaystyle=-\frac{1}{3}\overrightarrow{JG}$		(1.46)
		$\displaystyle=-\frac{1}{3}(\vec{v}+\vec{u}).$		(1.47)

Agora, vamos formar o vetor $\overrightarrow{HB}$ . Isso pode ser feito da seguinte forma

$\displaystyle\overrightarrow{HB}$	$\displaystyle=\overrightarrow{WQ}$	(1.48)
	$\displaystyle=\vec{u}+\overrightarrow{PQ}$	(1.49)
	$\displaystyle=\vec{u}+\overrightarrow{HI}$	(1.50)
	$\displaystyle=\vec{u}-\frac{1}{3}(\vec{v}+\vec{u})$	(1.51)
	$\displaystyle=\frac{2}{3}\vec{u}-\frac{1}{3}\vec{v}.$	(1.52)

Por tudo isso, concluímos que

$\displaystyle\overrightarrow{HC}$	$\displaystyle=\overrightarrow{HI}+\overrightarrow{HB}$	(1.53)
	$\displaystyle=-\frac{1}{3}(\vec{v}+\vec{u})$	(1.54)
	$\displaystyle+\frac{2}{3}\vec{u}-\frac{1}{3}\vec{v}$	(1.55)
	$\displaystyle=\frac{1}{3}\vec{u}-\frac{2}{3}\vec{v}.$	(1.56)

ER 1.3.2.

Mostre que $\vec{u}+\vec{v}=\vec{v}+\vec{u}$ .

Resolução.

Seja $A B C D$ o paralelogramo com $\vec{u}=\overrightarrow{AB}=\overrightarrow{DC}$ e $\vec{v}=\overrightarrow{AD}=\overrightarrow{BC}$ . Logo, pela regra do paralelogramo temos

$\displaystyle\vec{u}+\vec{v}$	$\displaystyle=\overrightarrow{AB}+\overrightarrow{BC}$	(1.57)
	$\displaystyle=\overrightarrow{AC}$	(1.58)
	$\displaystyle=\overrightarrow{AD}+\overrightarrow{DC}$	(1.59)
	$\displaystyle=\vec{v}+\vec{u}.$	(1.60)

Exercícios

E. 1.3.1.

Complete as lacunas.

a)

Se $\vec{u}=\overrightarrow{FE}$ e $\vec{v}=\overrightarrow{EG}$ , então $\vec{u}+\vec{v}=$ $\overrightarrow{FG}$ .
b)

$2\vec{0}+\vec{u}=$ $\overrightarrow{\vec{u}}$ .
c)

Pela associatividade da adição de vetores, temos $(\vec{w}+\vec{v})+\vec{u}$ $=\vec{w}+(\vec{v}+\vec{u})$ .
d)

Pela comutatividade da adição, temos $\vec{w}+\vec{u}=\vec{u}+\vec{w}$ .

a) $\overrightarrow{FG}$ . b) $\vec{u}$ . c) $(\vec{w}+\vec{v})+\vec{u}$ . d) comutatividade da adição.

E. 1.3.2.

Complete as lacunas.

a)

O vetor oposto de $\vec{u}=\overrightarrow{HA}$ é $-\vec{u}=$ $\overrightarrow{AH}$ .
b)

$-\vec{w}$ $+\vec{w}=\vec{0}$ .
c)

Pela definição de vetor oposto, $\left\|-\vec{v}\right\|=$ $\left\|\vec{v}\right\|$ .
d)

Se $\vec{u}=\overrightarrow{AB}$ e $\vec{v}=\overrightarrow{AC}$ , então $\vec{u}-\vec{v}=$ $\overrightarrow{CB}$ .

a) $\overrightarrow{AH}$ . b) $-\vec{w}$ . c) $\left\|\vec{v}\right\|$ . d) $\overrightarrow{CB}$ .

E. 1.3.3.

Complete as lacunas.

a)

O vetor $3\vec{w}$ tem o mesmo sentido oposto do vetor $\vec{w}$ .
b)

O vetor $-\pi\vec{v}$ tem o mesmo sentido oposto do vetor $\vec{v}$ .
c)

$\left\|-2\vec{w}\right\|=$ $2\left\|\vec{w}\right\|$ .
d)

Pela compatibilidade da multiplicação por escalar, temos $\beta(\alpha\vec{v})=(\beta\alpha)\vec{v}$ para quaisquer escalares $\alpha,\beta$ e vetor $\vec{v}$ .
e)

Pela distributividade, temos $\beta(\vec{v}+\vec{u})$ $=\beta\vec{v}+\beta\vec{u}$ para quaisquer escalar $\beta$ e vetores $\vec{u},\vec{v}$ .
f)

Outra forma de distributividade, fornece $(\beta+\alpha)\vec{w}=\beta\vec{w}+\alpha\vec{w}$ para quaisquer escalares $\alpha,\beta$ e vetor $\vec{w}$ .

a) mesmo; -x-. b) -x-; oposto. c) $2\left\|\vec{w}\right\|$ . d) compatibilidade da multiplicação. e) $\beta(\vec{v}+\vec{u})$ . f) distributividade.

E. 1.3.4.

Com base na figura abaixo, forneça uma representação de cada um dos seguintes vetores:

a)

$\overrightarrow{v}+\overrightarrow{u}$ .
b)

$3\vec{u}$ .
c)

$-\vec{v}$ .
d)

$\vec{u}-\vec{v}$ .
e)

$\vec{v}-\vec{u}$ .
f)

$\vec{v}+2\vec{u}$ .

a) $\overrightarrow{JG}$ . b) $\overrightarrow{WB}$ . c) $\overrightarrow{JF}$ . d) $\overrightarrow{NC}$ . e) $\overrightarrow{CN}$ . f) $\overrightarrow{KA}$ .

E. 1.3.5.

Com base na figura abaixo, forneça uma representação do vetor $\vec{w}+\vec{v}+\vec{u}$ .

$\overrightarrow{MJ}$ .

E. 1.3.6.

Com base na figura abaixo, escreva os seguintes vetores como resultado de operações envolvendo $\vec{u}$ ou $\vec{v}$ .

a)

$\overrightarrow{QK}$
b)

$\overrightarrow{KI}$
c)

$\overrightarrow{TO}$
d)

$\overrightarrow{PE}$
e)

$\overrightarrow{FT}$

a) $\frac{1}{2}\vec{v}$ ; b) $-\frac{2}{3}\vec{u}$ ; c) $\frac{1}{2}\vec{v}+\frac{1}{3}\vec{u}$ ; d) $\vec{v}+\frac{1}{3}\vec{u}$ ; e) $-\frac{4}{3}\vec{u}-\frac{3}{2}\vec{v}$

E. 1.3.7.

Seja dado um vetor $\vec{u}\neq 0$ . Calcule a norma do vetor⁶⁶endnote: ⁶ $\vec{u}/|\vec{u}|$ é chamado de vetor $\vec{u}$ normalizado, ou a normalização do vetor $\vec{u}$ . $\vec{v}=\vec{u}/|\vec{u}|$ .

$|\vec{v}|=1$ .

E. 1.3.8.

Diga se é verdadeira ou falsa cada uma das seguintes afirmações. Justifique sua resposta.

1.

$\vec{u}+\vec{u}=2\vec{u}$
2.

$\vec{u}=-\vec{u}\Leftrightarrow\vec{u}=\vec{0}$ .

a) verdadeira; b) verdadeira.

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

$\displaystyle\\|\alpha\vec{u}\\|$	$\displaystyle=\\|-\alpha\vec{u}\\|$	(1.26)
	$\displaystyle=-\alpha\\|\vec{u}\\|$	(1.27)
	$\displaystyle=\|\alpha\|\\|\vec{u}\\|.$	(1.28)

Política de uso de dados

Política de uso de dados

Vetores

1.3 Operações elementares com vetores

1.3.1 Adição de vetores

Propriedades

1.3.2 Vetor oposto

Observação 1.3.1.

Propriedade

1.3.3 Subtração de vetores

Regra do paralelogramo

1.3.4 Multiplicação de vetor por escalar

Observação 1.3.2.

Proposição 1.3.1.

Demonstração.

Propriedades

1.3.5 Resumo das propriedades

Exercícios resolvidos

ER 1.3.1.

Resolução.

ER 1.3.2.

Resolução.

Exercícios

E. 1.3.1.

E. 1.3.2.

E. 1.3.3.

E. 1.3.4.

E. 1.3.5.

E. 1.3.6.

E. 1.3.7.

E. 1.3.8.

Envie seu comentário

	$\displaystyle\vec{u}+\vec{0}$	$\displaystyle=\overrightarrow{AB}+\overrightarrow{BB}$		(1.9)
		$\displaystyle=\overrightarrow{AB}=\vec{u}.$		(1.10)

$\displaystyle\left(\vec{u}+\vec{v}\right)+\vec{w}$	$\displaystyle=\left(\overrightarrow{AB}+\overrightarrow{BC}\right)+% \overrightarrow{CD}$	(1.12)
	$\displaystyle=\overrightarrow{AC}+\overrightarrow{CD}$	(1.13)
	$\displaystyle=\overrightarrow{AD},$	(1.14)

$\displaystyle\vec{u}+\left(\vec{v}+\vec{w}\right)$	$\displaystyle=\overrightarrow{AB}+\left(\overrightarrow{BC}+\overrightarrow{CD% }\right)$	(1.15)
	$\displaystyle=\overrightarrow{AB}+\overrightarrow{BD}$	(1.16)
	$\displaystyle=\overrightarrow{AD}.$	(1.17)

$\displaystyle\vec{u}+(-\vec{u})$	$\displaystyle=\overrightarrow{AB}+\overrightarrow{BA}$	(1.20)
	$\displaystyle=\overrightarrow{AA}$	(1.21)
	$\displaystyle=\vec{0}.$	(1.22)

	$\displaystyle\left\\|1\vec{u}\right\\|$	$\displaystyle=\|1\|\left\\|\vec{u}\right\\|$		(1.30)
		$\displaystyle=\left\\|\vec{u}\right\\|.$		(1.31)

$\displaystyle\left\\|\alpha(\beta\vec{u})\right\\|$	$\displaystyle=\left\|\alpha\right\|\left\\|\beta\vec{u}\right\\|$	(1.33)
	$\displaystyle=\left\|\alpha\right\|\left\|\beta\right\|\left\\|\vec{u}\right\\|$	(1.34)
	$\displaystyle=\left\|\alpha\beta\right\|\left\\|\vec{u}\right\\|$	(1.35)
	$\displaystyle=\left\\|(\alpha\beta)\vec{u}\right\\|.$	(1.36)

	$\displaystyle\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% (\alpha+\beta)\vec{u}=\alpha\vec{u}+\beta\vec{u}$		(1.37)
	$\displaystyle\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \alpha\left(\vec{u}+\vec{v}\right)=\alpha\vec{u}+\alpha\vec{v}$		(1.38)

	$\displaystyle\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% (\alpha+\beta)\vec{u}=\alpha\vec{u}+\beta\vec{u}$		(1.44)
	$\displaystyle\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \alpha(\vec{u}+\vec{v})=\alpha\vec{u}+\alpha\vec{v}$		(1.45)