1.8 Seleção de Aplicações

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

Em revisão

1.8.1 Sistemas de Equações

Em revisão

Consideramos o seguinte problema de equações diferenciais ordinárias com valores de contorno

	$\displaystyle-u_{0}^{\prime\prime}+u_{1}=f_{0},\forall x\in(0,L)$		(1.190)
	$\displaystyle-u_{1}^{\prime\prime}+u_{0}=f_{1},\forall x\in(0,L)$		(1.191)
	$\displaystyle u_{0}(0)=u_{00},\quad u_{0}(L)=u_{0L},$		(1.192)
	$\displaystyle u_{1}(0)=u_{10},\quad u_{1}(L)=u_{1L},$		(1.193)

onde $f_{0}$ , $f_{1}$ , $u_{00}$ , $u_{0L}$ , $u_{10}$ , $u_{1L}$ são dados.

Para construirmos uma aproximação por elementos finitos podemos tomar o seguinte problema fraco associado: encontrar $u=(u_{0},u_{1})\in V_{0}\times V_{1}$ tal que

a(u,v)=L(v),\forall v=(v_{0},v_{1})\in V\times V,

(1.194)

onde $V_{0}=\{v\in H^{1}(I);\leavevmode\nobreak\ v_{0}(0)=u_{00},\leavevmode\nobreak% \ v_{0}(L)=u_{0L}\}$ , $V_{1}=\{v_{1}\in H^{1}(I);\leavevmode\nobreak\ v_{1}(0)=u_{10},\leavevmode% \nobreak\ v_{1}(L)=u_{1L}\}$ , $V=\{v\in H^{1}(I);\leavevmode\nobreak\ v(0)=v(L)=0\}$ , a forma bilinear é

a(u,v)=\int_{I}u_{0}^{\prime}v_{0}^{\prime}\,dx+\int_{I}u_{1}^{\prime}v_{1}^{% \prime}\,dx+\int_{I}u_{1}v_{0}\,dx+\int_{I}u_{0}v_{1}\,dx

(1.195)

e a forma linear é

L(v)=\int_{I}f_{0}v_{0}\,dx+\int_{I}f_{1}v_{1}\,dx.

(1.196)

Então, o problema de elemento finitos associado no espaço das funções lineares por partes lê-se: encontrar $u_{h}=(u_{h0},u_{h1})\in V_{h0}\times V_{h1}$ tal que

a(u_{h},v_{h})=L(v_{h}),\forall v_{h}=(v_{h0},v_{h1})\in V_{h}\times V_{h},

(1.197)

onde $V_{h0}=\{v_{h}\in P_{1}(I);\leavevmode\nobreak\ v_{h0}(0)=u_{00},\leavevmode% \nobreak\ v_{h0}(L)=u_{0L}\}$ , $V_{h1}=\{v_{h1}\in P_{1}(I);\leavevmode\nobreak\ v_{h1}(0)=u_{10},\leavevmode% \nobreak\ v_{h1}(L)=u_{1L}\}$ , $V_{h}=\{v_{h}\in P_{1}(I);\leavevmode\nobreak\ v_{h}(0)=v_{h}(L)=0\}$ .

Exemplo 1.8.1.

Consideramos o seguinte problema de valor de contorno

	$\displaystyle-u_{0}^{\prime\prime}+u_{1}=\operatorname{sen}(x)+\cos(x),\forall x% \in(-\pi,\pi)$		(1.198)
	$\displaystyle-u_{1}^{\prime\prime}+u_{0}=\cos(x)-\sin(x),\forall x\in(-\pi,\pi)$		(1.199)
	$\displaystyle u_{0}(-\pi)=0,\quad u_{0}(\pi)=0,$		(1.200)
	$\displaystyle u_{1}(-\pi)=-1,\quad u_{1}(\pi)=-1.$		(1.201)

Considerando elementos lineares por partes, temos a seguinte formulação de elementos finitos: encontrar $u_{h}=(u_{h0},u_{h1})\in V_{h0}\times V_{h1}$ tal que

a(u_{h},v_{h})=L(v_{h}),\forall v_{h}=(v_{h0},v_{h1})\in V_{h}\times V_{h},

(1.202)

onde $V_{h0}=\{v_{h}\in P_{1}(I);\leavevmode\nobreak\ v_{h0}(0)=v_{h0}(L)=0\}$ , $V_{h1}=\{v_{h1}\in P_{1}(I);\leavevmode\nobreak\ v_{h1}(0)=v_{h1}(L)=-1\}$ , $V_{h}=\{v_{h}\in P_{1}(I);\leavevmode\nobreak\ v_{h}(0)=v_{h}(L)=0\}$ , com as formas bilinear e linear são dadas em (1.195) e (1.196), respectivamente.

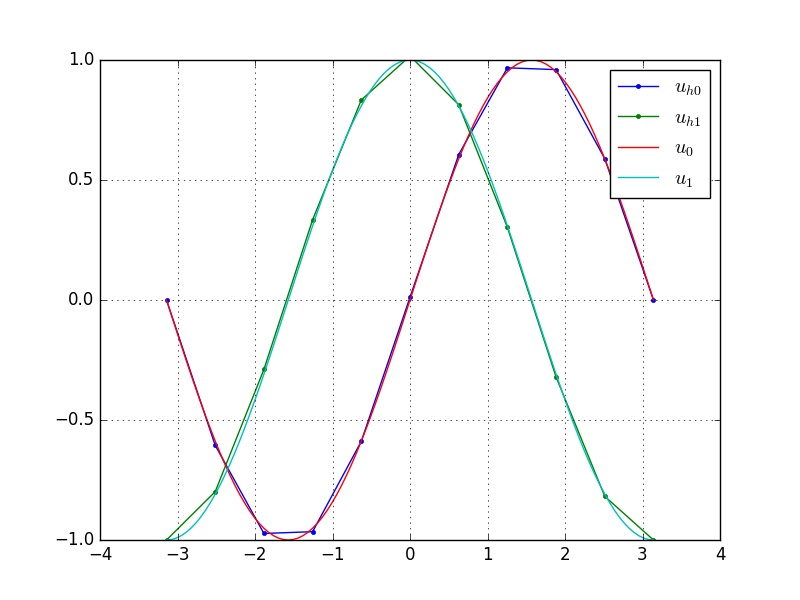
A Figura 1.8 apresenta o esboço dos gráficos das soluções analíticas $u_{0}(x)=\operatorname{sen}(x)$ e $u_{1}(x)=\cos(x)$ e de suas aproximações de elementos finitos $u_{h0}$ e $u_{h1}$ , estas construídas no espaço dos polinômios lineares por partes sobre uma malha uniforme de $5$ células.

Refer to caption — Figura 1.8: Esboço dos gráficos das soluções referentes ao Exemplo 1.8.1.

Com o FEniCS, a computação do problema de elementos finitos pode ser feita com o seguinte código:

from __future__ import print_function, division
from fenics import *
import numpy as np
import matplotlib.pyplot as plt

#tolerance
tol=1e-14

# malha
mesh = IntervalMesh(10,-pi,pi)

# espaco
P1 = FiniteElement(’P’,interval,1)
element = MixedElement([P1,P1])
V = FunctionSpace(mesh, element)

#C.C.
def boundary(x,on_boundary):
    return on_boundary

bc = [DirichletBC(V.sub(0),Constant(0.0),boundary),
      DirichletBC(V.sub(1),Constant(-1.0),boundary)]
print(bc)

#MEF problem
u = TrialFunction(V)
v = TestFunction(V)
f0 = Expression(’sin(x[0]) + cos(x[0])’,
                degree=10)
f1 = Expression(’cos(x[0]) - sin(x[0])’,
                degree=10)
a  = u[0].dx(0)*v[0].dx(0)*dx
a += u[1]*v[0]*dx
a += u[1].dx(0)*v[1].dx(0)*dx
a -= u[0]*v[1]*dx
L  = f0*v[0]*dx
L += f1*v[1]*dx

#computa a sol
u = Function(V)
solve(a == L, u, bc)

#sol analitica
u0a = Expression(’sin(x[0])’,
                 degree=10)
u1a = Expression(’cos(x[0])’,
                 degree=10)

plot(u[0],mesh=mesh,marker=’.’,label=r"$u_{h0}$")
plot(u[1],mesh=mesh,marker=’.’,label=r"$u_{h1}$")
mesh = IntervalMesh(100,-pi,pi)
plot(u0a,mesh=mesh,label=r"$u_0$")
plot(u1a,mesh=mesh,label=r"$u_1$")
plt.legend(numpoints=1)
plt.grid(’on’)
plt.show()

1.8.2 Exercícios

Em construção

Envie seu comentário

As informações preenchidas são enviadas por e-mail para o desenvolvedor do site e tratadas de forma privada. Consulte a Política de Uso de Dados para mais informações. Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

| | | |