Colabore! Saiba mais screen_rotation

Ao navegar por este site , você concorda com a Política de Uso de Dados.

| | | | |

4 Integração 4.1 Integração Autoadaptativa Referências

4.2 Integrais múltiplas

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

Vamos trabalhar com métodos para a computação de integrais múltiplas

\int\int_{R}f(x,y)\,dA.

(4.13)

Em uma região retangular $A=[a,b]\times[c,d]$ , podemos reescrevê-la como uma integral iterada

\int\int_{R}f(x,y)\,dA=\int_{a}^{b}\int_{c}^{d}f(x,y)\,dy\,dx.

(4.14)

4.2.1 Regras de Newton-Cotes

Regra do Trapézio

A Regra do Trapézio⁵⁹⁵⁹endnote: ⁵⁹Notas de Aula - Matemática Numérica. nos fornece

\int_{c}^{d}f(x,y)\,dy=\frac{h_{y}}{2}\left[f(x,c)+f(x,d)\right]-\frac{h_{y}^{% 3}}{12}f^{\prime\prime}(x,\eta)

(4.15)

com $h_{y}=(d-c)$ e $\eta\in(c,d)$ . De forma iterada, temos

	$\displaystyle\int_{a}^{b}\int_{c}^{d}f(x,y)\,dy\,dx$	$\displaystyle=\frac{h_{y}}{2}\int_{a}^{b}f(x,c)\,dx+\frac{h_{y}}{2}\int_{a}^{b% }f(x,d)\,dx$		(4.16)
		$\displaystyle-\frac{h_{y}^{3}}{12}\int_{a}^{b}f^{\prime\prime}(x,\eta)\,dx.$		(4.17)

Então, à exceção do termo do erro, aplicamos a Regra do Trapézio para as integrais em $x$ . Obtemos

$\displaystyle\int_{a}^{b}\int_{c}^{d}f(x,y)\,dy\,dx$	$\displaystyle=\frac{h_{y}}{2}\frac{h_{x}}{2}\left[f(a,c)+f(b,c)\right]$	(4.18)
	$\displaystyle+\frac{h_{y}}{2}\frac{h_{x}}{2}\left[f(a,d)+f(b,d)\right]$	(4.19)
	$\displaystyle-\frac{h_{y}}{2}\frac{h_{x}^{3}}{12}f^{\prime\prime}(\mu^{\prime}% ,c)$	(4.20)
	$\displaystyle-\frac{h_{y}}{2}\frac{h_{x}^{3}}{12}f^{\prime\prime}(\mu^{\prime% \prime},d)$	(4.21)
	$\displaystyle-\frac{h_{y}^{3}}{12}\int_{a}^{b}f^{\prime\prime}(x,\eta)\,dx,$	(4.22)

com $h_{x}=(b-a)$ , $\mu^{\prime},\mu^{\prime\prime}\in(a,b)$ . Pelos Teorema do Valor Intermediário e pelo Teorema do Valor Médio, podemos ver que o erro é $O(h_{x}h_{y}^{3}+h_{x}^{3}h_{y})$ . Por fim, obtemos a Regra do Trapézio para Integrais Iteradas

	$\displaystyle\int_{a}^{b}\int_{c}^{d}f(x,y)\,dy\,dx$	$\displaystyle=\frac{h_{y}}{2}\frac{h_{x}}{2}\left[f(a,c)+f(b,c)+f(b,d)+f(a,d)\right]$		(4.23)
		$\displaystyle+O(h_{x}h_{y}^{3}+h_{x}^{3}h_{y}).$		(4.24)

Exemplo 4.2.1.

A Regra do Trapézio fornece

\int_{1.5}^{2}\int_{1}^{1.5}\ln(x+2y)\,dy\,dx\approx 0.36.

(4.25)

Verifique!

Regra de Simpson

A Regra do Simpson⁶⁰⁶⁰endnote: ⁶⁰Notas de Aula - Matemática Numérica. nos fornece

	$\displaystyle\int_{c}^{d}f(x,y)\,dy$	$\displaystyle=\frac{h_{y}}{3}\left[f(x,y_{1})+4f(x,y_{2})+f(x,y_{3})\right]$		(4.26)
		$\displaystyle-\frac{h_{y}^{5}}{90}f^{(4)}(x,\eta)$		(4.27)

com $h_{y}=(d-c)/2$ , $y_{j}=(j-1)h_{y}$ , $j=1,2,3$ , e $\eta\in(c,d)$ . De forma iterada, temos

	$\displaystyle\int_{a}^{b}\int_{c}^{d}f(x,y)\,dy\,dx$	$\displaystyle=\frac{h_{y}}{3}\left[\int_{a}^{b}f(x,y_{1})\,dx+4\int_{a}^{b}f(x% ,y_{2})\,dx+\int_{a}^{b}f(x,y_{3})\,dx\right]$		(4.28)
		$\displaystyle-\frac{h_{y}^{5}}{90}\int_{a}^{b}f^{(4)}(x,\eta)\,dx$		(4.29)

Então, à exceção do termo do erro, aplicamos a Regra de Simpson para as integrais em $x$ . Obtemos

$\displaystyle\int_{a}^{b}\int_{c}^{d}f(x,y)\,dy\,dx$	$\displaystyle=\frac{h_{x}h_{y}}{9}\left[f(x_{1},y_{1})+4f(x_{2},y_{1})+f(x_{3}% ,y_{1})\right]$	(4.30)
	$\displaystyle+\frac{4h_{x}h_{y}}{9}\left[f(x_{1},y_{2})+4f(x_{2},y_{2})+f(x_{3% },y_{2})\right]$	(4.31)
	$\displaystyle+\frac{h_{x}h_{y}}{9}\left[f(x_{1},y_{3})+4f(x_{2},y_{3})+f(x_{3}% ,y_{3})\right]$	(4.32)
	$\displaystyle-\frac{h_{x}^{5}h_{y}}{270}f^{(4)}(\mu_{1},y_{1})$	(4.33)
	$\displaystyle-\frac{4h_{x}^{5}h_{y}}{270}f^{(4)}(\mu_{2},y_{2})$	(4.34)
	$\displaystyle-\frac{h_{x}^{5}h_{y}}{270}f^{(4)}(\mu_{3},y_{3})$	(4.35)
	$\displaystyle-\frac{h_{y}^{5}}{90}\int_{a}^{b}f^{(4)}(x,\eta)\,dx$	(4.36)

com $h_{x}=(b-a)/2$ , $\mu_{1},\mu_{2},\mu_{3}\in(a,b)$ . Pelos Teorema do Valor Intermediário e Teorema do Valor Médio, podemos ver que o erro é $O(h_{x}h_{y}^{5}+h_{x}^{5}h_{y})$ . Por fim, obtemos a Regra de Simpson para Integrais Iteradas

$\displaystyle\int_{a}^{b}\int_{c}^{d}f(x,y)\,dy\,dx$	$\displaystyle=\frac{h_{x}h_{y}}{9}\left[f(x_{1},y_{1})+4f(x_{2},y_{1})+f(x_{3}% ,y_{1})\right]$	(4.37)
	$\displaystyle+\frac{4h_{x}h_{y}}{9}\left[f(x_{1},y_{2})+4f(x_{2},y_{2})+f(x_{3% },y_{2})\right]$	(4.38)
	$\displaystyle+\frac{h_{x}h_{y}}{9}\left[f(x_{1},y_{3})+4f(x_{2},y_{3})+f(x_{3}% ,y_{3})\right]$	(4.39)
	$\displaystyle+O(h_{x}h_{y}^{5}+h_{x}^{5}h_{y}).$	(4.40)

Exemplo 4.2.2.

A Regra de Simpson fornece

\int_{1.5}^{2}\int_{1}^{1.5}\ln(x+2y)\,dy\,dx\approx 0.361003.

(4.41)

Verifique!

4.2.2 Regras Compostas de Newton-Cotes

A ideia é particionar a região de integração em células e o resultado da integração é a soma da aplicação da regra de quadratura em cada uma das células.

Regra Composta do Trapézio

Para uma região retangular $R=[a,b]\times[c,d]$ , vamos construir a malha

M=\{c_{k}=[x_{i},x_{i+1}]\times[y_{j},y_{j+1}]:\leavevmode\nobreak\ k=i+(j-1)n% _{x}\},

(4.42)

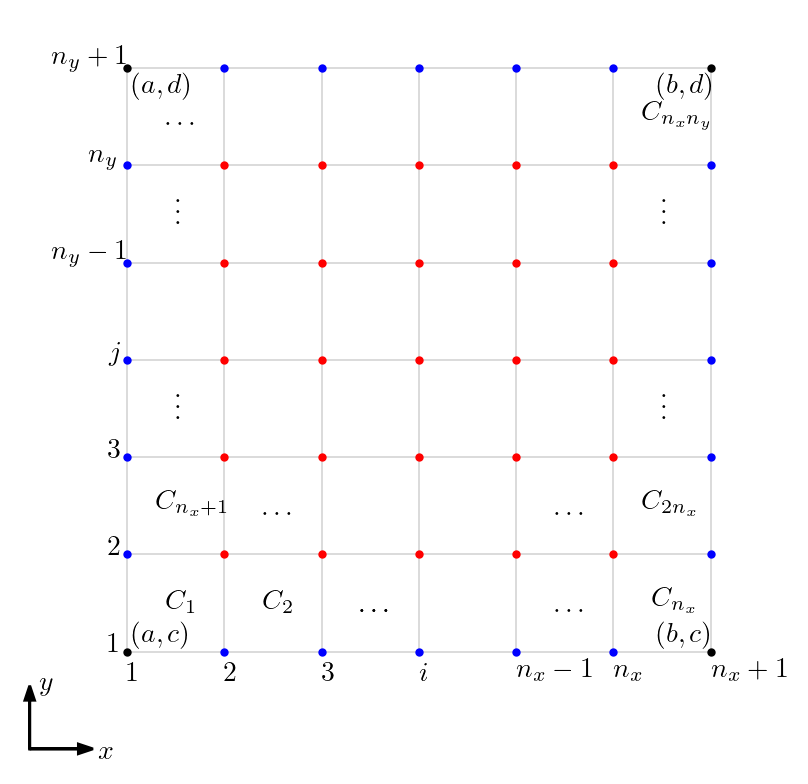
onde $x_{i}=(i-1)h_{x}$ , $h_{x}=(b-a)/n_{x}$ , $i=1,2,\dotsc,n_{x}+1$ e $y_{j}=(j-1)h_{y}$ , $h_{y}=(d-c)/n_{y}$ , $j=1,2,\dotsc,n_{y}+1$ . Consulte a Figura 4.1.

Refer to caption — Figura 4.1: Representação da malha para a Regra Composta do Trapézio.

Aplicando a ideia, temos

	$\displaystyle\int_{a}^{b}\int_{c}^{d}f(x,y)\,dy\,dx$	$\displaystyle=\sum_{k=1}^{n_{x}n_{y}}\int\int_{C_{k}}f(x,y)\,dy\,dx$		(4.43)
		$\displaystyle=\sum_{i=1}^{n_{x}}\sum_{j=1}^{n_{y}}\int_{x_{i}}^{x_{i+1}}\int_{% y_{j}}^{y_{j+1}}f(x,y)\,dy\,dx$		(4.44)

Em cada integral em $C_{k}$ , aplicamos a Regra do Trapézio, segue

	$\displaystyle\int_{x_{i}}^{x_{i+1}}\int_{y_{j}}^{y_{j+1}}f(x,y)\,dy\,dx$	$\displaystyle\approx\frac{h_{y}}{2}\frac{h_{x}}{2}\left[f(x_{i},y_{j})+f(x_{i+% 1},y_{j})\right.$		(4.45)
		$\displaystyle+\left.f(x_{i+1},y_{j+1})+f(x_{i+1},y_{j})\right]$		(4.46)

Observamos que nos conjuntos de nodos (marcados em azul na Figura 4.1)

	$\displaystyle\{(i,j):\leavevmode\nobreak\ i=2,\dotsc,n_{x},j=1\text{ ou }j=n_{% y}+1\},$		(4.47)
	$\displaystyle\{(i,j):\leavevmode\nobreak\ i=1\text{ ou }i=n_{x}+1,j=2,\dotsc,n% _{y}\}$		(4.48)

a função integranda será avaliada $2$ vezes. Já, em todos os nodos internos, $i=2,\dotsc,n_{x}$ , $j=2,\dotsc,n_{y}$ , a função será avaliada $4$ vezes. Com isso, chegamos à Regra Composta do Trapézio

$\displaystyle\int_{a}^{b}\int_{c}^{d}f(x,y)\,dy\,dx$	$\displaystyle=\frac{h_{x}h_{y}}{4}\left[f(x_{1},y_{1})+f(x_{n_{x}+1},y_{1})\right.$
	$\displaystyle\left.+f(x_{n_{x}+1},y_{n_{y}+1})+f(x_{1},y_{n_{y}+1})\right]$
	$\displaystyle+\frac{h_{x}h_{y}}{2}\sum_{i=2}^{n_{x}}\left[f(x_{i},y_{1})+f(x_{% i},y_{n_{y}+1})\right]$
	$\displaystyle+\frac{h_{x}h_{y}}{2}\sum_{j=2}^{n_{y}}\left[f(x_{1},y_{j})+f(x_{% n_{x}+1},y_{j})\right]$
	$\displaystyle+h_{x}h_{y}\sum_{i=2}^{n_{x}}\sum_{j=2}^{n_{y}}f(x_{i},y_{j})$
	$\displaystyle+O(h_{x}^{2}+h_{y}^{2})$	(4.49)

Observamos que esta é uma quadratura de $(n_{x}+1)(n_{y}+1)$ nodos.

E. 4.2.1.

Verifique a aplicação da Regra Composta do Trapézio para computar

\int_{1.5}^{2}\int_{1}^{1.5}\ln(x+2y)\,dy\,dx.

(4.50)

Regra Composta de Simpson

Aqui, vamos construir uma malha

M=\left\{C_{k}=[x_{i},x_{i+2}]\times[y_{j},y_{j+2}]:\leavevmode\nobreak\ i=1,3% ,\dotsc,n_{x}-1,j=1,3,\dotsc,n_{y}-1,\leavevmode\nobreak\ \right\},

(4.51)

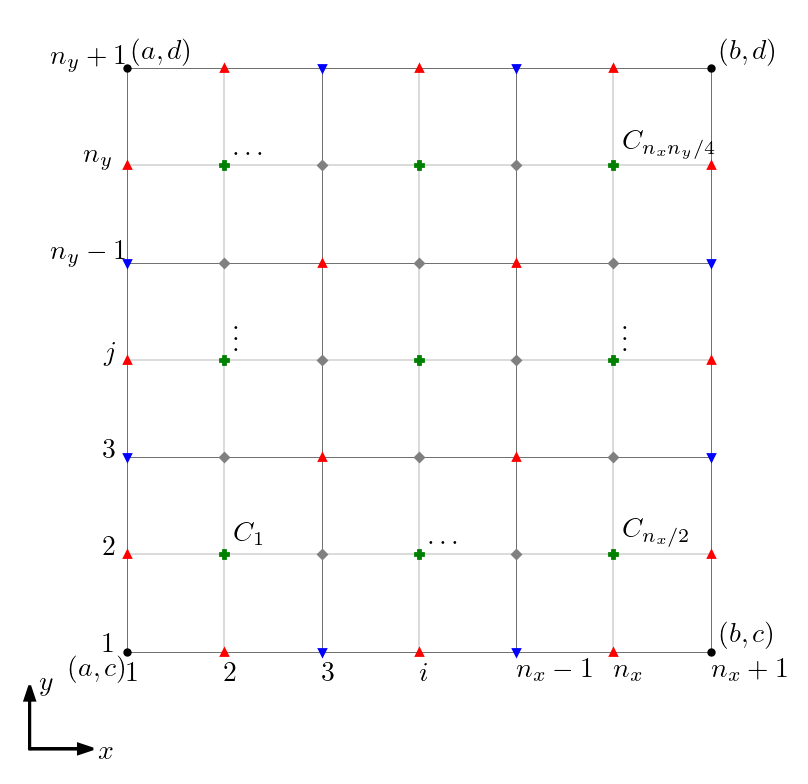
onde $x_{i}=(i-1)h_{x}$ , $h_{x}=(b-a)/n_{x}$ , $i=1,2,\dotsc,n_{x}+1$ e $y_{j}=(j-1)h_{y}$ , $h_{y}=(d-c)/n_{y}$ , $j=1,2,\dotsc,n_{y}+1$ . Com $n_{x},n_{y}\leq 2$ números pares. Consulte a Figura 4.2.

A Regra Composta de Simpson para Integrais Iteradas fica

$\displaystyle\int_{a}^{b}\int_{c}^{d}f(x,y)\,dx\,dy$	$\displaystyle=\frac{h_{x}h_{y}}{9}\left\{f(x_{1},y_{1})+f(x_{n_{x}+1},y_{1})\right.$
	$\displaystyle+f(x_{1},y_{n_{y}+1})+f(x_{n_{x}+1},y_{n_{y}+1})$
	$\displaystyle+2\sum_{i=1}^{n_{x}/2-1}\left[f(x_{2i+1},y_{1})+f(x_{2i+1},y_{n_{% y}+1})\right]$
	$\displaystyle+2\sum_{j=1}^{n_{y}/2-1}\left[f(x_{1},y_{2j+1})+f(x_{n_{x}+1},y_{% 2j+1})\right]$
	$\displaystyle+4\sum_{i=1}^{n_{x}/2}\left[f(x_{2i},y_{1})+f(x_{2i},y_{n_{y}+1})\right]$
	$\displaystyle+4\sum_{j=1}^{n_{y}/2}\left[f(x_{1},y_{2j})+f(x_{n_{x}+1},y_{2j})\right]$
	$\displaystyle+4\sum_{i=1}^{n_{x}/2-1}\sum_{j=1}^{n_{y}/2-1}f(x_{2j+1},y_{2j+1})$
	$\displaystyle+8\sum_{i=1}^{n_{x}/2-1}\sum_{j=1}^{n_{y}/2}f(x_{2i+1},y_{2j})$
	$\displaystyle+8\sum_{i=1}^{n_{x}/2}\sum_{j=1}^{n_{y}/2-1}f(x_{2i},y_{2j+1})$
	$\displaystyle\left.+16\sum_{i=1}^{n_{x}/2}\sum_{j=1}^{n_{y}/2}f(x_{2i},y_{2j})\right\}$
	$\displaystyle+O(h_{x}^{4}+h_{y}^{4}).$	(4.52)

E. 4.2.2.

Verifique a aplicação da Regra Composta de Simpson para computar

\int_{1.5}^{2}\int_{1}^{1.5}\ln(x+2y)\,dy\,dx.

(4.53)

Notas

1 Llewellyn Hilleth Thomas, 1903 - 1992, físico e matemático aplicado britânico. Fonte: Wikipedia.
2 Johann Carl Friedrich Gauss, 1777 - 1855, matemático alemão. Fonte: Wikipédia: Carl Friedrich Gauss.
3 Siméon Denis Poisson, 1781 - 1840, matemático francês. Fonte: Wikipédia:Siméon Denis Poisson.
4 Pierre-Simon Laplace, 1749 - 1827, matemático francês. Fonte: Wikipédia: Pierre-Simon Laplace.
5 CSR e CSC são formatos de matrizes esparsas mais eficientes para a computação matricial.
6 CSR é mais eficiente em muitos casos.
7 Use o método coo_matrix.tocsr().
8 scipy.sparse.linalg.spsolve é uma implementação do Método LU otimizado para matrizes esparsas.
9 Use o método coo_matrix.tocsc().
10 Consulte mais em Notas de Aula: Matemática Numérica.
11 Desenvolvido por Yousef Saad e H. Schultz, 1986. Fonte: Wikipedia.
12 Alexei Nikolajewitsch Krylov, 1863 - 1945, engenheiro e matemático russo. Fonte: Wikipédia.
13 Georgi Iwanowitsch Petrov, 1912 - 1987, engenheiro soviético. Fonte: Wikipedia.
14 Boris Galerkin, 1871 - 1945, engenheiro e matemático soviético. Fonte: Wikipédia.
15 Walter Edwin Arnoldi, 1917 - 1995, engenheiro americano estadunidense. Fonte: Wikipédia.
16 Jørgen Pedersen Gram, 1850 - 1916, matemático dinamarquês. Fonte: Wikipédia.
17 Erhard Schmidt, 1876 - 1959, matemático alemão. Fonte: Wikipédia.
18 Karl Adolf Hessenberg, 1904 - 1959, engenheiro e matemático alemão. Fonte: Wikipédia.
19 Alston Scott Householder, 1904 - 1993, matemático americano estadunidense. Fonte: Wikipédia.
20 Siméon Denis Poisson, 1781 - 1840, matemático francês. Fonte: Wikipédia:Siméon Denis Poisson.
21 Walter Edwin Arnoldi, 1917 - 1995, engenheiro americano estadunidense. Fonte: Wikipédia.
22 $x^{T}Ax>0$ para todo $x\neq 0$ .
23 Iteração do método do máximo declive.
24 Chamada de pesquisa linear exata. Qualquer outra escolha para $\alpha$ é conhecida como pesquisa linear não exata.
25 scipy.sparse.linalg.gmres
26 scipy.sparse.linalg.spsolve
27 Compare com o funcional $J$ dado em (1.87).
28 Mostre que $\left<\cdot,\cdot\right>_{A}$ é de fato um produto interno.
29 scipy.sparse.linalg.gmres
30 scipy.sparse.linalg.cg
31 Carl Gustav Jakob Jacobi, 1804 - 1851, matemático alemão. Fonte: Wikipédia: Carl Gustav Jakob Jacobi.
32 Isaac Newton, 1642 - 1727, matemático, físico, astrônomo, teólogo e autor inglês. Fonte: Wikipédia: Isaac Newton.
33 Rudolf Otto Sigismund Lipschitz, 1832 - 1903, matemático alemão. Fonte: Wikipédia.
34 Jan Burgers, 1895 - 1981, físico neerlandês. Fonte: Wikipédia: Jan Burgers.
35 Johann Peter Gustav Lejeune Dirichlet, 1805 - 1859, matemático alemão. Fonte: Wikipédia: Johann Peter Gustav Lejeune Dirichlet.
36 Erich Hans Rothe, 1895 - 1988, matemático alemão. Fonte: Wikipédia.
37 Leonhard Paul Euler, 1707-1783, matemático e físico suíço. Fonte: Wikipédia: Ronald Fisher.
38 Isaac Newton, 1642 - 1727, matemático, físico, astrônomo, teólogo e autor inglês. Fonte: Wikipédia: Isaac Newton.
39 Carl Gustav Jakob Jacobi, 1804 - 1851, matemático alemão. Fonte: Wikipédia: Carl Gustav Jakob Jacobi.
40 Brook Taylor, 1685 - 1731, matemático britânico. Fonte: Wikipédia:Brook Taylor.
41 Philip Wolfe, 1927 - 2016, matemático estadunidense. Fonte: Wikipédia.
42 Howard Harry Rosenbrock, 1920 - 2010, engenheiro britânico. Fonte: Wikipedia: Howard Harry Rosenbrock.
43 Leopold Kronecker, 1923 - 1891, matemático alemão. Fonte: Wikipédia: Leopold Kronecker.
44 Howard Harry Rosenbrock, 1920 - 2010, engenheiro britânico. Fonte: Wikipedia: Howard Harry Rosenbrock.
45 Isaac Newton, 1642 - 1727, matemático, físico, astrônomo, teólogo e autor inglês. Fonte: Wikipédia: Isaac Newton.
46 Alexei Nikolajewitsch Krylov, 1863 - 1945, engenheiro e matemático russo. Fonte: Wikipédia.
47 Howard Harry Rosenbrock, 1920 - 2010, engenheiro britânico. Fonte: Wikipedia: Howard Harry Rosenbrock.
48 Howard Harry Rosenbrock, 1920 - 2010, engenheiro britânico. Fonte: Wikipedia: Howard Harry Rosenbrock.
49 Existe uma base de $\mathbb{C}^{n\times n}$ formada apenas de autovetores de $A$ .
50 Segue por indução matemática.
51 Condição necessária para a convergência.
52 Issai Schur, 1875 - 1941, matemático russo-alemão. Fonte: Wikipédia.
53 Uma matriz $U$ é dita unitária quando $U^{-1}=U^{H}$ .
54 Uma matriz $Q$ é dita ortogonal quando $Q^{T}Q=I$ .
55 Karl Adolf Hessenberg, 1904 - 1959, matemático e engenheiro alemão. Fonte: Wikipédia.
56 Alston Scott Householder, 1904 - 1993, matemático estadunidense. Fonte: Wikipédia.
57 James Wallace Givens Jr., 1910 - 1993, matemático estadunidense. Fonte: Wikipédia.
58 Consulte mais sobre a Regra de Simpson em Seção 10.1 Regras de Newton-Cotes.
59 Notas de Aula - Matemática Numérica.
60 Notas de Aula - Matemática Numérica.

Envie seu comentário

As informações preenchidas são enviadas por e-mail para o desenvolvedor do site e tratadas de forma privada. Consulte a Política de Uso de Dados para mais informações. Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

| | | |