Colabore! Saiba mais screen_rotation

Ao navegar por este site , você concorda com a Política de Uso de Dados.

| | | | |

6 Arquivos e Gráficos 6.1 Arquivos 7 Orientação a Objetos

6.2 Gráficos

Compre o e-book deste material aqui!

Vamos usar o pacote computacional matplotlib para a elaboração de gráficos de funções. Usualmente, vamos utilizar os seguintes módulos Python

⬇

1import matplotlib as mpl

2import matplotlib.pyplot as plt

3import numpy as np

O submódulo matplotlib.pyplot é uma interface do matplotlib para a plotagem simples gráficos e de forma iterativa. Por padrão, o módulo matplotlib é importado como mlp e seu submódulo matplotlib.pyplot como plt.

6.2.1 Área Gráfica

No matplotlib, os gráficos são colocados em um container Figure, uma janela gráfica ou um arquivo de imagem). O container pode ter um ou mais Axes, uma área gráfica contendo todos os elementos de um gráfico (eixos, pontos, linhas, anotações, legendas, etc.). Podemos usar Axes.plot para plotar dados.

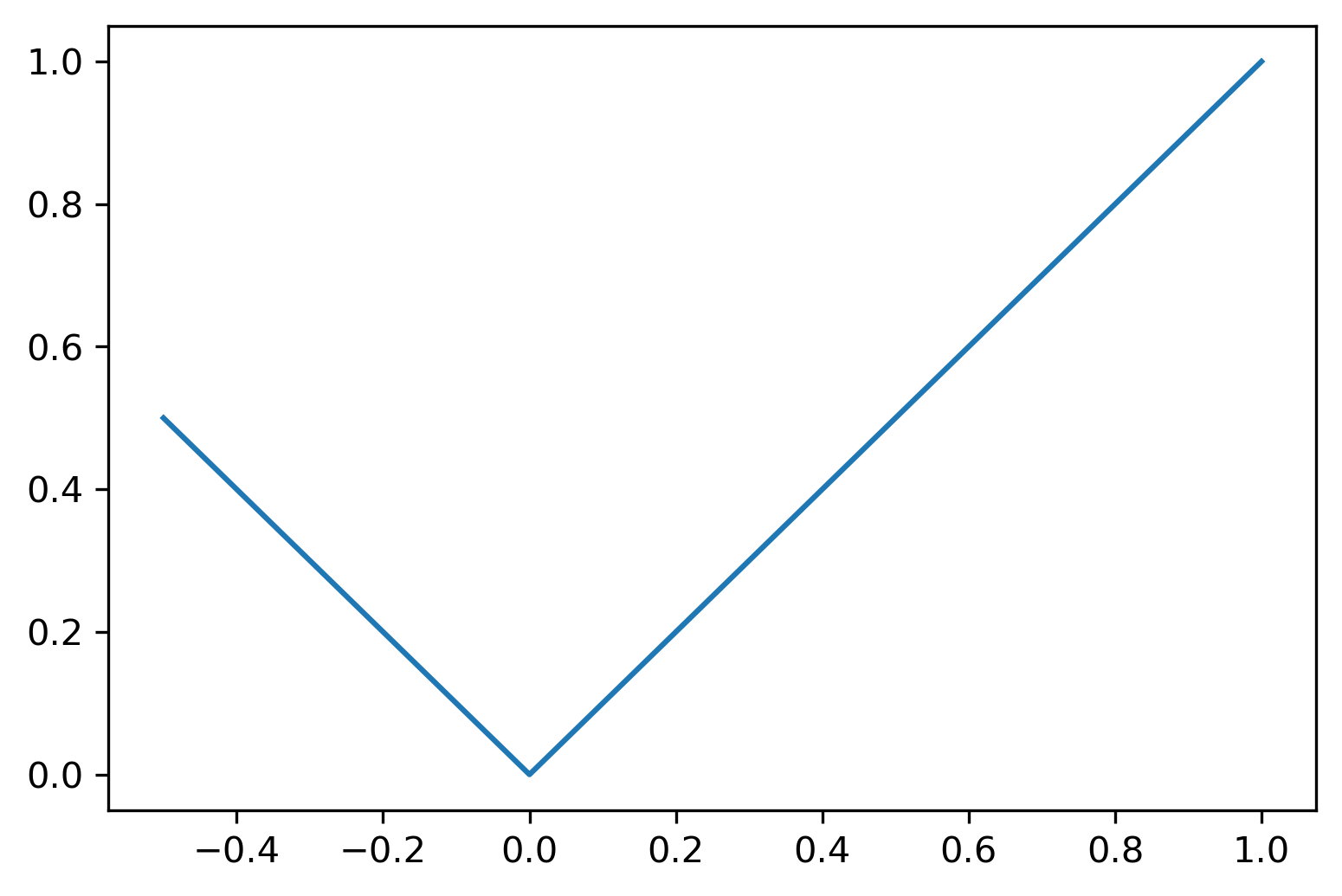
Refer to caption — Figura 6.1: Gráfico referente ao Exemplo 6.2.1.

Exemplo 6.2.1.

Consideramos a função

f(x)=|x|,\leavevmode\nobreak\ -\frac{1}{2}\leq x<1.

(6.3)

A Figura 6.1, mostra o gráfico de $f$ plotado com o código abaixo.

⬇

1import matplotlib.pyplot as plt

3# figure

4fig = plt.figure()

5# axes

6ax = fig.add_subplot()

7# plot

8ax.plot([-0.5, 0, 1],

9 [0.5, 0, 1])

10# display

11plt.show()

No caso de curvas, podemos usamos um número adequado de pontos de forma que os segmentos de linhas fiquem imperceptíveis a olho nu.

Exemplo 6.2.2.

Consideramos a função

f(x)=\left\{\begin{array}[]{ll}-(x+1)^{2}-2&,\leavevmode\nobreak\ -2\leq x<-% \frac{1}{2},\\ |x|&,\leavevmode\nobreak\ -\frac{1}{2}\leq x<1,\\ (x-2)^{3}+2,&,\leavevmode\nobreak\ 1\leq x<3.\end{array}\right.

(6.4)

A Figura 6.2, mostra o gráfico de $f$ plotado com o código abaixo.

⬇

1import matplotlib as mpl

2import matplotlib.pyplot as plt

3import numpy as np

5# figure

6fig = plt.figure()

7# axis

8ax = fig.add_subplot()

9# -2 <= x < -0.5

10x = np.linspace(-2, -0.5)

11ax.plot(x, -(x+1)**2-2)

12# -0.5 <= x < 1

13x = np.linspace(-0.5, 1)

14ax.plot(x, np.fabs(x))

15# 1 <= x < 3

16x = np.linspace(1, 3)

17ax.plot(x, (x-2)**3+2)

18# display

19plt.show()

6.2.2 Eixos

No matplotlib, os eixos⁴¹⁴¹endnote: ⁴¹Não confundir com Axes, um objeto que contém todos os elementos de um gráfico. de um gráfico são objetos da classe Axis.

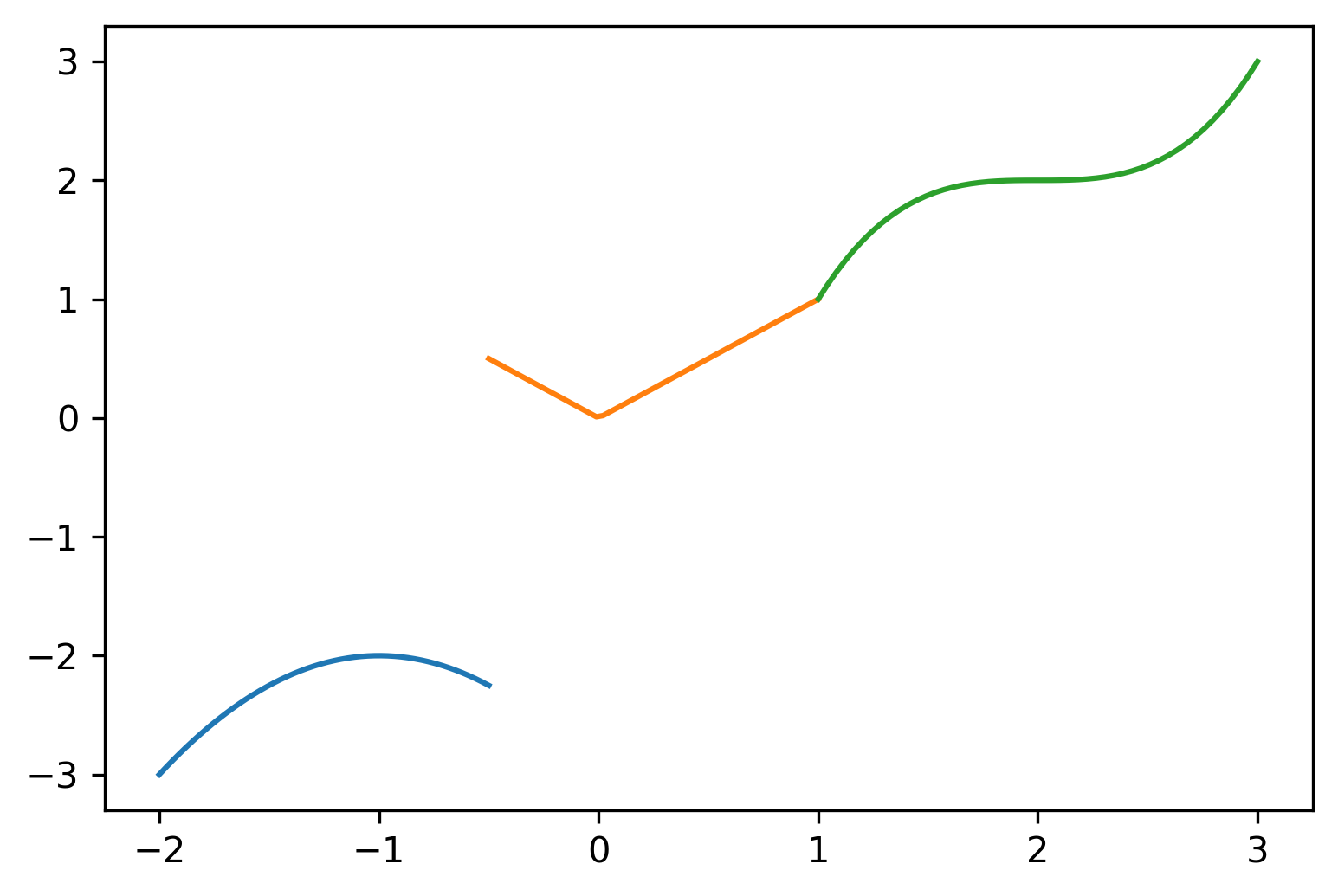
Exemplo 6.2.3.

Com o código abaixo, produzimos a Figura 6.3, a qual contém o gráfico da função do Exemplo 6.2 com os eixos editados.

⬇

1import matplotlib as mpl

2import matplotlib.pyplot as plt

3import numpy as np

5# figure

6fig = plt.figure()

7# axis

8ax = fig.add_subplot()

9# -2 <= x < -0.5

10x = np.linspace(-2, -0.5)

11ax.plot(x, -(x+1)**2-2)

12# -0.5 <= x < 1

13x = np.linspace(-0.5, 1)

14ax.plot(x, np.fabs(x))

15# 1 <= x < 3

16x = np.linspace(1, 3)

17ax.plot(x, (x-2)**3+2)

18# eixo-x

19ax.set_xlim((-2.1, 3.1))

20ax.set_xticks([-2, -1, 0, 1, 2, 3])

21ax.set_xlabel('x')

22#eixo-y

23ax.set_ylim((-3.1, 3.1))

24ax.set_yticks([-3, -2, -1, 0, 1, 2, 3])

25ax.set_ylabel('y')

26# grid

27ax.grid()

28# display

29plt.savefig('fig.png', bbox_inches='tight')

30plt.savefig('fig.pdf', bbox_inches='tight')

31plt.show()

6.2.3 Elementos Gráficos

No matplotlib, os elementos gráficos (basicamente tudo o que é visível, pontos, linhas, eixos, etc.) são objetos da classe Artist.

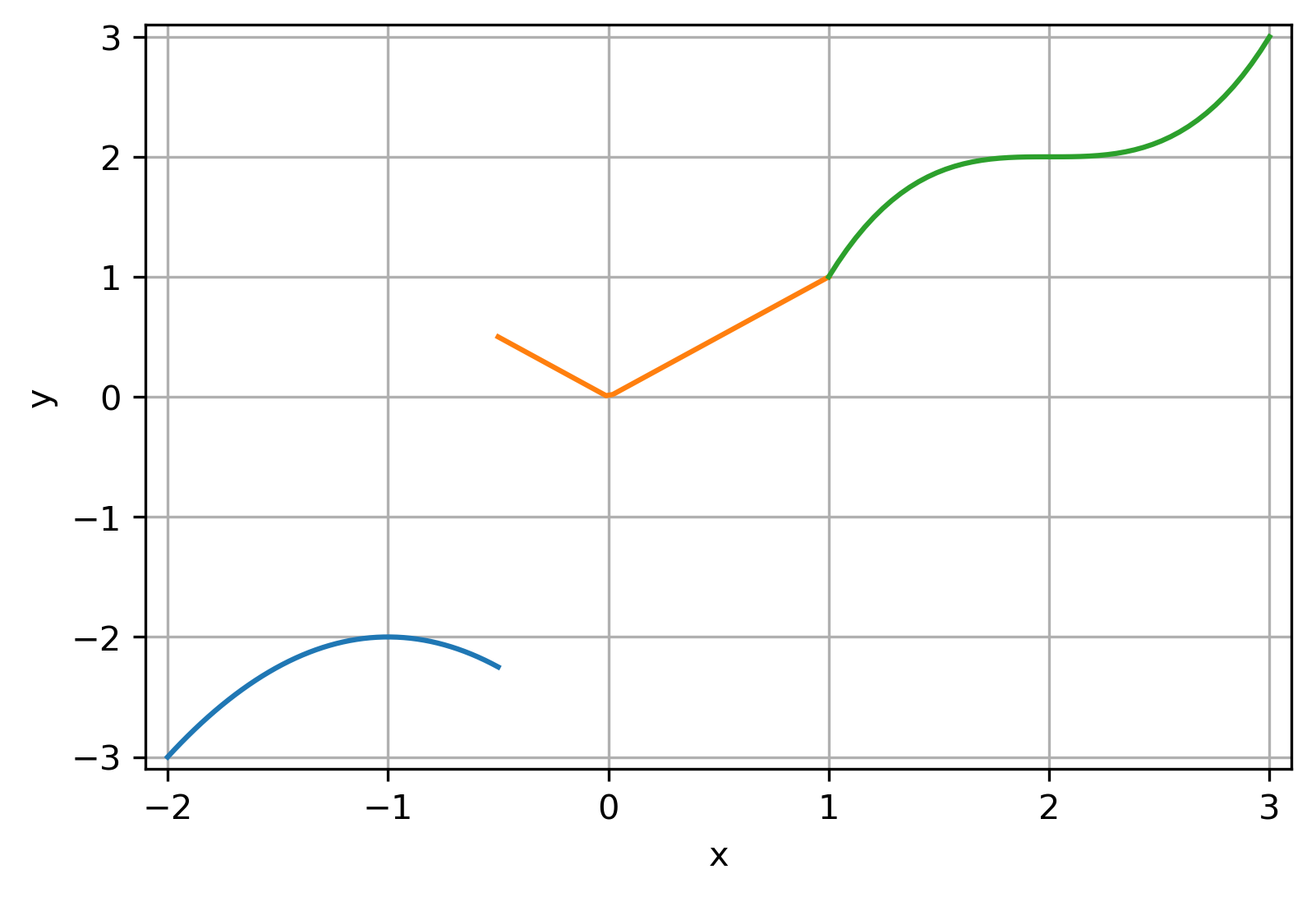
Exemplo 6.2.4.

Com o código abaixo, produzimos a Figura 6.4, a qual contém o gráfico da função do Exemplo 6.4 com os eixos editados.

⬇

1import matplotlib as mpl

2import matplotlib.pyplot as plt

3import numpy as np

5# figure

6fig = plt.figure()

7# axis

8ax = fig.add_subplot()

10# -2 <= x < -0.5

11x = np.linspace(-2, -0.5)

12f1 = lambda x: -(x+1)**2-2

13ax.plot(x, f1(x), color='blue',

14 label='-(x+1)^2-2')

15ax.plot([-2.], f1(-2.), linestyle='', marker='o',

16 color='blue')

17ax.plot([-0.5], f1(-0.5), ls='', marker='o',

18 markerfacecolor='white', markeredgecolor='blue')

20# -0.5 <= x < 1

21x = np.linspace(-0.5, 1)

22f2 = lambda x: np.fabs(x)

23ax.plot(x, f2(x), color='orange', label='|x|')

24ax.plot([-0.5], [f2(-0.5)], ls='', marker='o',

25 color='orange')

27ax.plot([-0.5, -0.5], [f1(-0.5), f2(-0.5)],

28 ls = '--', color='gray', alpha=0.5)

30# 1 <= x < 3

31x = np.linspace(1, 3)

32f3 = lambda x: (x-2)**3+2

33ax.plot(x, f3(x), color='green',

34 label='(x-2)^3+2')

35ax.plot([1.], [f3(1.)], ls='', marker='o',

36 color='green')

37ax.plot([3.], [f3(3.)], ls='', marker='o',

38 mfc='white', mec='green')

40# eixo-x

41ax.set_xlim((-2.1, 3.1))

42ax.set_xticks([-2, -1, 0, 1, 2, 3])

43ax.set_xlabel('x')

44# eixo-y

45ax.set_ylim((-3.1, 3.1))

46ax.set_yticks([-3, -2, -1, 0, 1, 2, 3])

47ax.set_ylabel('y')

48# grid

49ax.grid()

50ax.legend()

51# display

52plt.savefig('fig.png', bbox_inches='tight')

53plt.savefig('fig.pdf', bbox_inches='tight')

54plt.show()

6.2.4 Textos e Anotações

O comando Axes.text permite adicionar elementos string a um Axes. Anotações, consistem em um apontamento, e podem ser adicionadas com o comando Axes.annotate. Elementos texto suportam LATEXusando-se o marcador de texto $.

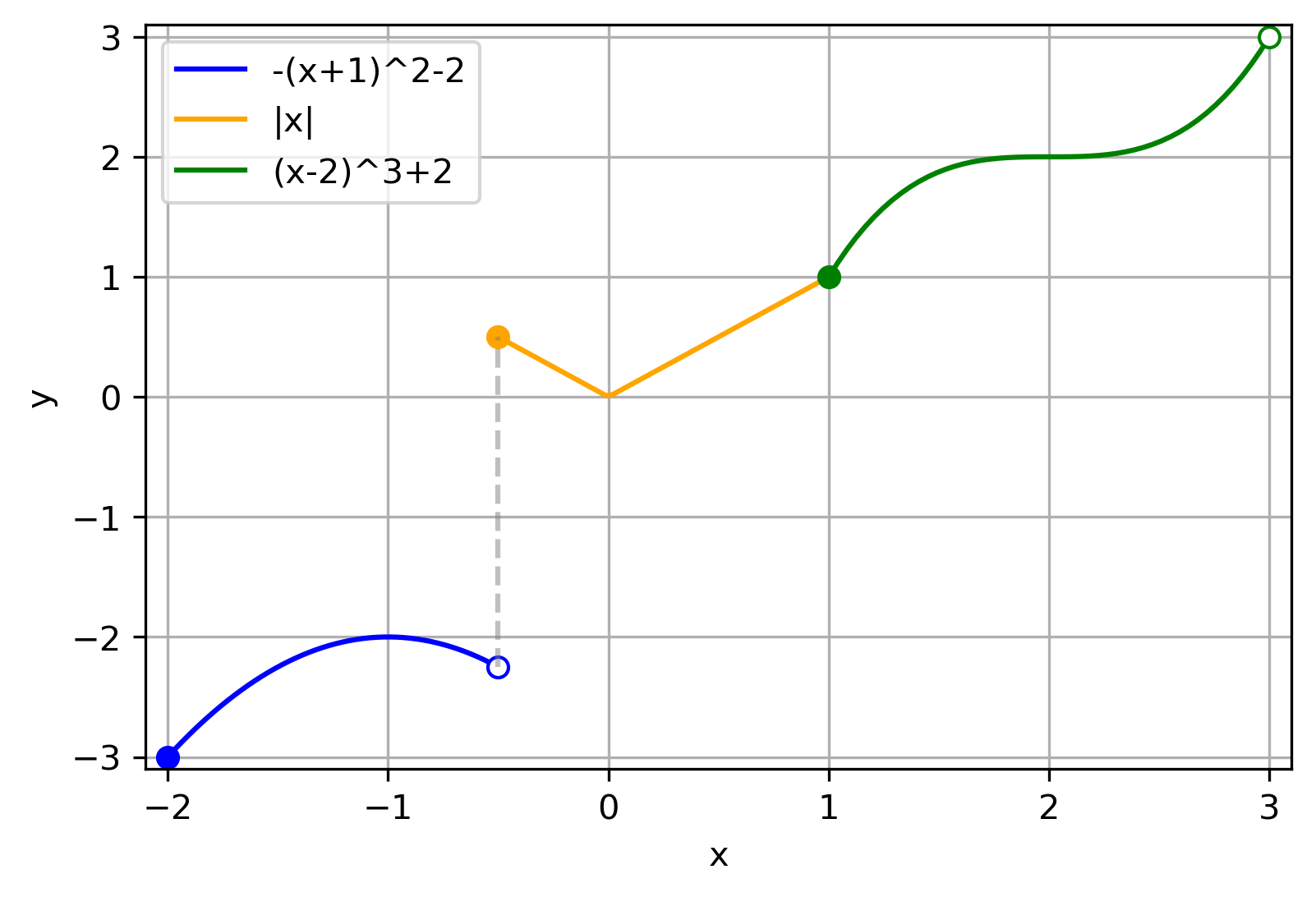
Exemplo 6.2.5.

Com o código abaixo, produzimos a Figura 6.5, a qual contém o gráfico da função do Exemplo 6.5 com os eixos editados.

⬇

1import matplotlib as mpl

2import matplotlib.pyplot as plt

3import numpy as np

5# figure

6fig = plt.figure()

7# axis

8ax = fig.add_subplot()

10# -2 <= x < -0.5

11x = np.linspace(-2, -0.5)

12f1 = lambda x: -(x+1)**2-2

13ax.plot(x, f1(x), color='blue',

14 label='$y=-(x+1)^2-2$')

15ax.plot([-2.], f1(-2.), linestyle='', marker='o',

16 color='blue')

17ax.plot([-0.5], f1(-0.5), ls='', marker='o',

18 markerfacecolor='white', markeredgecolor='blue')

20# -0.5 <= x < 1

21x = np.linspace(-0.5, 1)

22f2 = lambda x: np.fabs(x)

23ax.plot(x, f2(x), color='orange', label='$y=|x|$')

24ax.plot([-0.5], [f2(-0.5)], ls='', marker='o',

25 color='orange')

27ax.plot([-0.5, -0.5], [f1(-0.5), f2(-0.5)],

28 ls = '--', color='gray', alpha=0.5)

29# anotação

30ax.annotate('mín. local', xy=(0,0), xytext=(0.1,-0.6),

31 arrowprops={'arrowstyle':'->'})

33# 1 <= x < 3

34x = np.linspace(1, 3)

35f3 = lambda x: (x-2)**3+2

36ax.plot(x, f3(x), color='green',

37 label='$y=(x-2)^3+2$')

38ax.plot([1.], [f3(1.)], ls='', marker='o',

39 color='green')

40ax.plot([3.], [f3(3.)], ls='', marker='o',

41 mfc='white', mec='green')

43# hachurando

44ax.fill_between(x, f3(x), color='gray', alpha=0.25)

45ax.plot([1., 1.], [0., f3(1.)],

46 ls='--', color='gray', alpha=0.5)

47ax.plot([3., 3.], [0., f3(3.)],

48 ls='--', color='gray', alpha=0.5)

49# texto

50ax.text(1.5, 0.9, '$\\int_{1}^3 (x-2)^3+2\,dx$')

52# eixo-x

53ax.set_xlim((-2.1, 3.1))

54ax.set_xticks([-2, -1, 0, 1, 2, 3])

55ax.set_xlabel('$x$')

56# eixo-y

57ax.set_ylim((-3.1, 3.1))

58ax.set_yticks([-3, -2, -1, 0, 1, 2, 3])

59ax.set_ylabel('$y$')

60# grid

61ax.grid()

62ax.legend()

63# display

64plt.savefig('fig.png', bbox_inches='tight')

65plt.savefig('fig.pdf', bbox_inches='tight')

66plt.show()

6.2.5 Exercícios

E. 6.2.1.

Use o Matplotlib para produzir um gráfico para as seguintes funções:

a)

$\displaystyle f(x)=x^{2}$ , $-2\leq x\leq 2$ .
b)

$\displaystyle g(x)=2x^{3}+2$ , $-3\leq x\leq 0$ .
c)

$\displaystyle h(x)=\operatorname{sen}(x)$ , $-\pi\leq x\leq\pi$ .

E. 6.2.2.

Use o Matplotlib para plotar o gráfico da função sigmoid

f(x)=\frac{1}{1+e^{-x}}.

(6.5)

Na mesma área gráfica, plote retas tracejadas identificando suas assíntotas horizontais.

Resposta.

Dica: $y=0$ e $y=1$ são assíntotas horizontais da função sigmoid.

E. 6.2.3.

Use o Matplotlib para plotar o gráfico de $f(x)=1/x$ , $-2\leq x\leq 2$ . Na mesma área gráfica, plote uma reta tracejada identificando a assíntota vertical de $f$ .

Resposta.

Dica: $x=0$ é assíntota vertical de $f$ .

E. 6.2.4.

Use o Matplotlib para produzir um gráfico para a seguinte função definida por partes

f(x)=\left\{\begin{array}[]{ll}\cos(x)&,-\pi<x\leq 0,\\ 1-x^{2}&,0<x\leq 2.\end{array}\right.

(6.6)

Use de marcadores para identificar os pontos extremos de cada parte da função. Também, adicione o label de cada eixo e uma legenda para identificar cada parte da função.

E. 6.2.5.

Em uma mesma área gráfica, plote as curvas $y=x+1$ e $y=x^{2}$ , e marque seus pontos de interseção. Para cada um destes pontos, inclua a anotação “pto. de interseção”.

E. 6.2.6.

No gráfico da função sigmoid

f(x)=\frac{1}{1+e^{-x}}

(6.7)

hachure (pinte) a região que corresponde a área associada a integral definida

\int_{1}^{3}f(x)\,dx.

(6.8)

Resposta.

Dica: use a função Axes.fill_between.

Exemplo 6.2.6.

Em uma mesma área gráfica, plote a área entre as curvas $y=x+1$ e $y=x^{2}$ , $x=-1$ e $x=2$ .

Envie seu comentário

As informações preenchidas são enviadas por e-mail para o desenvolvedor do site e tratadas de forma privada. Consulte a Política de Uso de Dados para mais informações. Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

| | | |