Método dos Elementos Finitos

1 Problemas Unidimensionais 1.3 Condições de Contorno 1.5 Aplicação: EDP Evolutiva

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

1.4 Malhas Auto-Adaptativas

Em revisão

Retornemos ao problema modelo (1.59)-(1.60)

	$\displaystyle-u^{\prime\prime}$	$\displaystyle=f,\quad x\in I=[0,L],$		(1.159)
	$\displaystyle u(0)$	$\displaystyle=u(L)=0.$		(1.160)

A estimativa a posteriori dada no Teorema 1.2.4, indica que os elementos residuais $\eta_{i}(u_{h})$ podem ser utilizados para estimarmos a precisão da aproximação por elementos finitos. Ou seja, espera-se que quanto menores forem os elementos residuais, mais precisa é a solução por elementos finitos. Além disso, como

\eta_{i}(u_{h})=h_{i}\|f-u_{h}^{\prime\prime}\|_{L^{2}(I_{i})},

(1.161)

podemos reduzir $\eta_{i}(u_{h})$ diminuindo o tamanho da célula $I_{i}$ .

Do observado acima, motiva-se o seguinte algoritmo de elementos finitos com refinamento automático de malha:

1.

Escolhemos uma malha inicial.
2.
Iteramos:
1. 2.
  
  Resolvemos o problema de elementos finitos na malha corrente.
2. 2.
  
  Computamos $\eta_{i}(u_{h})$ em cada célula da malha corrente.
3. 2.
  
  Com base na malha corrente, Contruímos uma nova malha pelo refinamento das células com os maiores valores de $\eta_{i}(u_{h})$ .
4. 2.
  
  Verificamos o critério de parada.

Uma estratégia clássica para a escolha das células a serem refinadas é a seguinte: refina-se a $i$ -ésima célula se

\eta_{i}(u_{h})>\alpha\max_{j=1,2,\dotsc,n}\eta_{j}(u_{h}),

(1.162)

onde escolhemos $0<\alpha<1$ .

Exemplo 1.4.1.

Consideramos o problema

	$\displaystyle-u^{\prime\prime}$	$\displaystyle=e^{-100\|x-\frac{1}{2}\|},\quad x\in I=[0,1],$		(1.163)
	$\displaystyle u(0)$	$\displaystyle=u(1)=0.$		(1.164)

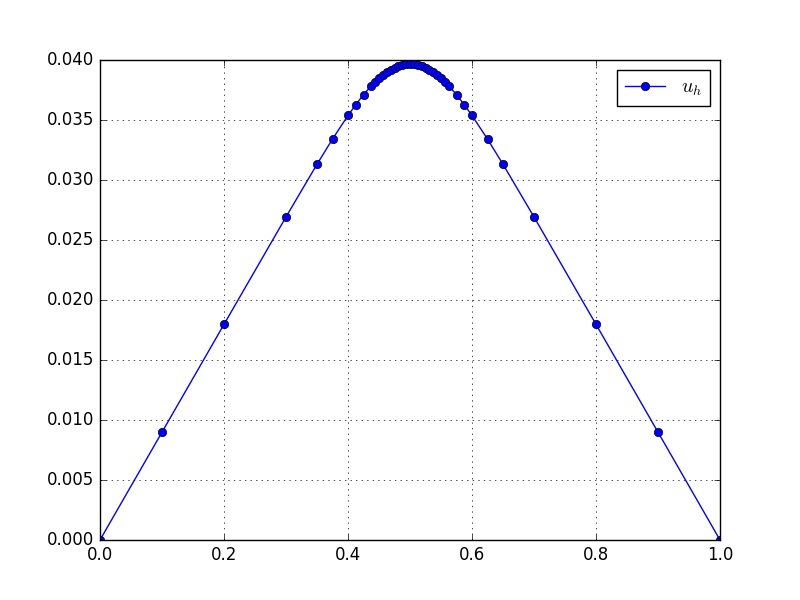
Aqui, computamos aproximações de elementos finitos no espaço das funções lineares por partes $V_{h,0}=\{v\in P_{1}(I);\leavevmode\nobreak\ v(0)=v(1)=0\}$ com sucessivos refinamentos de malha. Utilizamos uma malha inicial uniforme com 10 células e fazemos, então, 5 refinamentos sucessivos utilizando como critério de refinamento a estratégia (1.162) com $\alpha=0,5$ . A Figura 1.7 apresenta o esboço do gráfico da solução de elementos finitos na malha mais refinada. Além disso, na Tabela 1.1 temos os o número de células e o $\eta_{i}(u_{h})$ máximo respectivo.

Refer to caption — Figura 1.7: Esboço dos gráficos das soluções referentes ao Exemplo 1.4.1.

#malha	#células	$\max_{i}\eta_{i}(u_{h})$
0	10	5.0E-03
1	12	2.0E-03
2	14	8.6E-04
3	22	2.9E-04
4	30	1.4E-04
5	38	6.1E-05

Tabela 1.1: Resultados referente ao Exemplo 1.4.1.

Com o FEniCS, a computação do problema de elementos finitos pode ser feita com o seguinte código:

from __future__ import print_function, division
from fenics import *
import numpy as np
import matplotlib.pyplot as plt

# malha
mesh = IntervalMesh(10,0,1)

# espaco
V = FunctionSpace(mesh, ’P’, 1)

# fonte
f = Expression(’exp(-100*pow(fabs(x[0]-0.5),2))’,degree=1)

# condicoes de contorno
def boundary(x,on_boundary):
    return on_boundary

#iteracoes
for iter in np.arange(6):

    #problema
    bc = DirichletBC(V,Constant(0.0),boundary)
    u = TrialFunction(V)
    v = TestFunction(V)
    a = u.dx(0)*v.dx(0)*dx
    L = f*v*dx

    #resolve
    u = Function(V)
    solve(a == L, u, bc)

    #grafico
    plt.close(’all’)
    xx = mesh.coordinates()[:,0]
    sorted_indices =  np.argsort(xx)
    yy = u.compute_vertex_values()
    plt.plot(xx[sorted_indices],yy[sorted_indices],
                 marker="o",label=r"$u_h$")
    plt.legend(numpoints=1)
    plt.grid(’on’)
    plt.show()

    DG = FunctionSpace(mesh, "DG", 0)
    v = TestFunction(DG)
    a = CellVolume(mesh)
    eta = assemble(f**2*v*a*dx)

    # refinamento da malha
    cell_markers = MeshFunction("bool", mesh, mesh.topology().dim(), False)
    eta_max = np.amax(eta[:])
    print(eta_max)
    print("%d %d %1.1E\n" % (iter,mesh.num_cells(),eta_max))
    alpha = 0.5
    for i,cell in enumerate(cells(mesh)):
        if (eta[i] > alpha*eta_max):
            cell_markers[cell] = True

    mesh = refine(mesh, cell_markers)
    V = FunctionSpace(mesh, ’P’, 1)

1.4.1 Exercícios

Em revisão

E. 1.4.1.

Use uma estratégia de sucessivos refinamentos globais para resolver o problema dado no Exemplo 1.4.1. Compare seus resultados com aqueles obtidos no exemplo.

Código.

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Política de uso de dados