Matemática numérica I

6 Aproximação por mínimos quadrados 6.1 Problemas lineares Referências

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

6.2 Problemas não lineares

Em revisão

Um problema não linear de mínimos quadrados consiste em ajustar uma dada função

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}y=f(x;\bm{c})

(6.31)

que dependa não linearmente dos parâmetros $\bm{c}=(c_{1},c_{2},\dotsc,c_{m})$ , $m\geq 1$ , a um dado conjunto de $n\geq m$ pontos $\{(x_{i},y_{i})\}_{i=1}^{n}$ . Mais especificamente, buscamos resolver o seguinte problema de minimização

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\min_{\{c_{1}% ,c_{2},\dotsc,c_{m}\}}\left[E:=\sum_{i=1}^{n}\left(y_{i}-f(x_{i};c)\right)^{2}% \right].

(6.32)

Aqui, denotaremos por $r(c\bm{)}:=(r_{1}(\bm{c}),r_{2}(\bm{c}),\dotsc,r_{n}(\bm{c}))$ o vetor dos resíduos $r_{i}(\bm{c}):=y_{i}-f(x_{i},\bm{c})$ . Com isso, o problema se resume a encontrar o vetor de parâmetros $\bm{c}$ que minimiza

E=\|r(\bm{c})\|^{2}.

(6.33)

Tais parâmetros são solução do seguinte sistema de equações

\frac{\partial E}{\partial c_{j}}=2\sum_{i=1}^{n}r_{i}(\bm{c})\frac{\partial}{% \partial c_{j}}r_{i}(\bm{c})=0

(6.34)

ou, equivalentemente, da equação

\nabla E=0\Leftrightarrow J_{R}^{T}(\bm{c})r(\bm{c})=0,

(6.35)

onde

J_{R}(\bm{c}):=\begin{bmatrix}\frac{\partial r_{1}}{\partial c_{1}}&\frac{% \partial r_{1}}{\partial c_{2}}&\cdots&\frac{\partial r_{1}}{\partial c_{m}}\\ \frac{\partial r_{2}}{\partial c_{1}}&\frac{\partial r_{2}}{\partial c_{2}}&% \cdots&\frac{\partial r_{2}}{\partial c_{m}}\\ \vdots&\vdots&\vdots&\vdots\\ \frac{\partial r_{n}}{\partial c_{1}}&\frac{\partial r_{n}}{\partial c_{2}}&% \cdots&\frac{\partial r_{n}}{\partial c_{m}}\end{bmatrix}

(6.36)

é a jacobiana do resíduo $r$ em relação aos parâmetros $\bm{c}$ .

Podemos usar o método de Newton para resolver (6.35). Para tanto, escolhemos uma aproximação inicial para $\bm{c}^{(1)}=(c_{1}^{(1)},c_{2}^{(1)},\dotsc,c_{m}^{(1)})$ e iteramos

	$\displaystyle H_{R}(c^{(k)})\delta^{(k)}=-J_{R}^{T}(c)r(c)$		(6.37)
	$\displaystyle c^{(k+1)}=c^{(k)}+\delta^{(k)},$		(6.38)

onde $\delta^{(k)}=(\delta_{1}^{(k)},\delta_{2}^{(k)},\delta_{m}^{(k)})$ é a atualização de Newton (ou direção de busca) e $H_{R}(c):=[h_{p,q}(c)]_{p,q=1}^{m,m}$ é a matriz hessiana, cujos elementos são

h_{p,q}:=\sum_{i=1}^{n}\left\{\frac{\partial r_{i}}{\partial c_{q}}\frac{% \partial r_{i}}{\partial c_{p}}+r_{i}\frac{\partial^{2}r_{i}}{\partial c_{q}% \partial c_{p}}\right\}.

(6.39)

Exemplo 6.2.1.

Consideremos o problema de ajustar, no sentido de mínimos quadrados, a função

f(x;c)=c_{1}e^{c_{2}x}

(6.40)

ao seguinte conjunto de pontos

$i$	$1$	$2$	$3$	$4$
$x_{i}$	$-1$	$0$	$1$	$1.5$
$y_{i}$	$8.0$	$1.5$	$0.2$	$0.1$

Aqui, vamos utilizar a iteração de Newton para o problema de mínimos quadrados, i.e. a iteração dada em (6.37)-(6.38). Para tanto, para cada $i=1,2,3,4$ , precisamos das seguintes derivadas parciais do resíduo $r_{i}(c):=y_{i}-c_{1}e^{c_{2}x_{i}}$ :

	$\displaystyle\frac{\partial}{\partial c_{1}}r_{i}(c)=-e^{c_{2}x_{i}},$		(6.41)
	$\displaystyle\frac{\partial}{\partial c_{2}}r_{i}(c)=-c_{1}x_{i}e^{c_{2}x_{i}},$		(6.42)
	$\displaystyle\frac{\partial^{2}}{\partial c_{1}^{2}}r_{i}(c)=0,$		(6.43)
	$\displaystyle\frac{\partial^{2}}{\partial c_{1}\partial c_{2}}r_{i}(c)=\frac{% \partial^{2}}{\partial c_{2}\partial c_{1}}r_{i}(c)=-x_{i}e^{c_{2}x_{i}},$		(6.44)
	$\displaystyle\frac{\partial^{2}}{\partial c_{2}^{2}}r_{i}(c)=-c_{1}x_{i}^{2}e^% {c_{2}x_{i}}.$		(6.45)

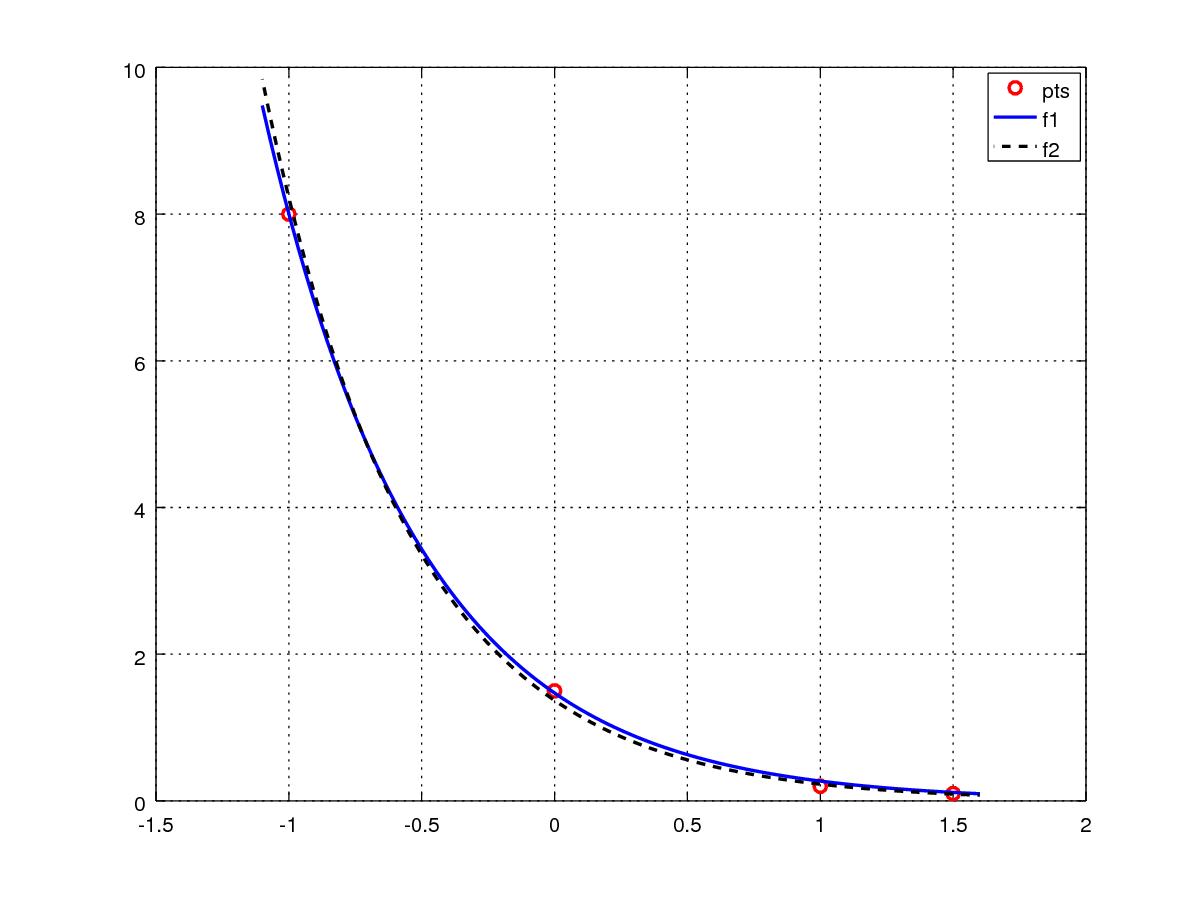
Refer to caption — Figura 6.4: Esboço da curva ajustada no Exemplo 6.2.1.

Com isso e tomando $c^{(1)}=(1.4,-1.8)$ (motivado do Exemplo LABEL:ex:mq_nlin0), computamos as iterações de Newton (6.37)-(6.38). Iterando até a precisão de $TOL=10^{-4}$ , obtemos a solução $c_{1}=1.471$ e $c_{2}=-1.6938$ . Na Figura 6.4 vemos uma comparação entre a curva aqui ajustada ( $-$ ) e aquela obtida no Exemplo LABEL:ex:mq_nlin0 ( $--$ ).

Observamos que a solução obtida no exemplo anterior (Exemplo 6.2.1) difere da previamente encontrada no Exemplo LABEL:ex:mq_nlin0. Naquele exemplo, os parâmetros obtidos nos fornecem $E=6.8\mathrm{e}\!-2\!$ , enquanto que a solução do exemplo anterior fornece $E=6.1\mathrm{e}\!-3\!$ . Isto é esperado, pois naquele exemplo resolvemos um problema aproximado, enquanto no exemplo anterior resolvemos o problema por si.

O emprego do método de Newton para o problema de mínimos quadrados tem a vantagem da taxa de convergência quadrática, entretanto requer a computação das derivadas parciais de segunda ordem do resíduo. Na sequência discutimos alternativas comumente empregadas.

6.2.1 Método de Gauss-Newton

Em revisão

O método de Gauss-Newton é uma técnica iterativa que aproxima o problema não linear de mínimos quadrados (6.32) por uma sequência de problemas lineares. Para seu desenvolvimento, começamos de uma aproximação inicial $c^{(1)}=(c_{1}^{(1)},c_{2}^{(1)},\dotsc,c_{m}^{(1)})$ dos parâmetros que queremos ajustar. Também, assumindo que a $n$ -ésima iterada $c^{(k)}$ é conhecida, faremos uso da aproximação de primeira ordem de $f(x,c)$ por polinômio de Taylor, i.e.

f(x;c^{(k+1)})\approx f(x;c^{(k)})+\nabla_{c}f(x;c^{(k)})(c^{(k+1)}-c^{(k)}),

(6.46)

onde

\nabla_{c}f(x;c)=\left[\frac{\partial}{\partial c_{1}}f(x;c)\leavevmode% \nobreak\ \frac{\partial}{\partial c_{2}}f(x;c)\leavevmode\nobreak\ \cdots% \leavevmode\nobreak\ \frac{\partial}{\partial c_{m}}f(x;c)\right].

(6.47)

O método consiste em obter a solução do problema não linear (6.32) pelo limite dos seguintes problemas lineares de mínimos quadrados

	$\displaystyle\min_{\delta^{(k)}}$	$\displaystyle\left[\tilde{E}:=\sum_{i=1}^{n}(y_{i}-f(x_{i},c^{(k)})-\nabla_{c}% f(x_{i};c^{(k)})\delta^{(k)})^{2}\right]$		(6.48)
		$\displaystyle c^{(k+1)}=c^{(k)}+\delta^{(k)}.$		(6.49)

Agora, usando a notação de resíduo $r(c)=y-f(x;c)$ , observamos que (6.55) consiste no problema linear de mínimos quadrados

\min_{\delta^{(k)}}\|r(c^{(k)})+J_{R}(c^{(k)})\delta^{(k)}\|_{2}^{2},

(6.50)

o qual é equivalente a resolver as equações normais

J_{R}^{T}(c^{(n)})J_{R}(c^{(n)})\delta^{(n)}=-J_{R}^{T}(c)r(c).

(6.51)

Com isso, dada uma aproximação inicial $c^{(1)}$ , a iteração do método de Gauss-Newton consiste em

	$\displaystyle J_{R}^{T}(c^{(k)})J_{R}(c^{(k)})\delta^{(k)}=-J_{R}^{T}(c)r(c)$		(6.52)
	$\displaystyle c^{(k+1)}=c^{(k)}+\delta^{(k)}.$		(6.53)

Exemplo 6.2.2.

A aplicação da iteração de Gauss-Newton ao problema de mínimos quadrados discutido no Exemplo 6.2.1 nos fornece a mesma solução obtida naquele exemplo (preservadas a aproximação inicial e a tolerância de precisão).

O método de Gauss-Newton pode ser lentamente convergente para problemas muito não lineares ou com resíduos grandes. Nesse caso, métodos de Gauss-Newton com amortecimento são alternativas robustas [1, 5]. Na sequência, introduziremos um destes métodos, conhecido como método de Levenberg-Marquardt.

6.2.2 Método de Levenberg-Marquardt

Em revisão

O método de Levenberg-Marquardt é uma variação do método de Gauss-Newton no qual a direção de busca $\delta^{(n)}$ é obtida da solução do seguinte problema regularizado

\min_{\delta^{(k)}}\{\|r(c^{(k)})+J_{R}(c^{(k)})\delta^{(k)}\|_{2}^{2}+\mu^{(k% )}\|\delta^{(k)}\|_{2}^{2}\}

(6.54)

ou, equivalentemente,

\min_{\delta^{(k)}}\left\|\begin{bmatrix}r(c^{(k)})\\ 0\end{bmatrix}+\begin{bmatrix}J_{R}(c^{(k)})\\ \mu^{(k)}I\end{bmatrix}\delta^{(k)}\right\|_{2}^{2}

(6.55)

A taxa de convergência das iterações de Levenberg-Marquardt é sensível a escolha do parâmetro $\mu^{(k)}\geq 0$ . Aqui, faremos esta escolha por tentativa e erro. O leitor pode aprofundar-se mais sobre esta questão na literatura especializada (veja, por exemplo, [1, 5]).

Observação 6.2.1.

Quando $\mu^{(k)}\equiv 0$ para todo $n$ , o método de Levenberg-Marquardt é equivalente ao método de Gauss-Newton.

Exemplo 6.2.3.

Consideremos o problema de mínimos quadrados discutido no Exemplo 6.2.1. O método de Gauss-Newton falha para este problema se escolhermos, por exemplo, $c^{(1)}=(0,0)$ . Isto ocorre pois, para esta escolha de $c^{(1)}$ , a jacobiana $J(c^{(1)})$ não tem posto completo. Entretanto, o método de Levenberg-Marquardt com $\mu^{(k)}=0.1$ é convergente, mesmo para esta escolha de $c^{(1)}$ .

6.2.3 Exercícios

Em revisão

E. 6.2.1.

Use o método de Gauss-Newton para ajustar, no sentido de mínimos quadrados e com precisão de $10^{-4}$ , a curva $y=c_{1}e^{c_{2}(x-c_{3})^{2}}$ aos pontos

$i$	$1$	$2$	$3$	$4$	$5$	$6$
$x_{i}$	$-0.5$	$0.5$	$1.3$	$2.1$	$2.7$	$3.1$
$y_{i}$	$0.1$	$1.2$	$2.7$	$0.9$	$0.2$	$0.1$

Use as condições iniciais:

a)

$c_{1}=2.1$ , $c_{2}=-1$ e $c_{3}=1.3$ .
b)

$c_{1}=1$ , $c_{2}=-1$ e $c_{3}=-1$ .

a) $c_{1}=2.69971\mathrm{e}\!+0\!$ , $c_{2}=-1.44723\mathrm{e}\!+0\!$ , $c_{3}=1.24333\mathrm{e}\!+0\!$ ; b) divergente.

E. 6.2.2.

Resolva o exercício anterior (E.6.2.1) usando o método de Levenberg-Marquardt com amortecimento constante $\mu=0.2$ .

a) $c_{1}=2.69971\mathrm{e}\!+0\!$ , $c_{2}=-1.44723\mathrm{e}\!+0\!$ , $c_{3}=1.24333\mathrm{e}\!+0\!$ ; b) $c_{1}=2.69971\mathrm{e}\!+0\!$ , $c_{2}=-1.44723\mathrm{e}\!+0\!$ , $c_{3}=1.24333\mathrm{e}\!+0\!$

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Política de uso de dados

Política de uso de dados

Matemática numérica I

6.2 Problemas não lineares

Exemplo 6.2.1.

6.2.1 Método de Gauss-Newton

Exemplo 6.2.2.

6.2.2 Método de Levenberg-Marquardt

Observação 6.2.1.

Exemplo 6.2.3.

6.2.3 Exercícios

E. 6.2.1.

E. 6.2.2.

Envie seu comentário