Deep Learning para Equações Diferenciais Parciais

3 Perceptron Multicamadas 3.2 Aplicação: Problema de Classificação Binária 3.4 Diferenciação Automática

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

3.3 Aplicação: Aproximação de Funções

Redes Perceptron Multicamadas (MLPs) são aproximadoras universais. Nesta seção, vamos aplicá-las na aproximação de funções uni- e bidimensionais.

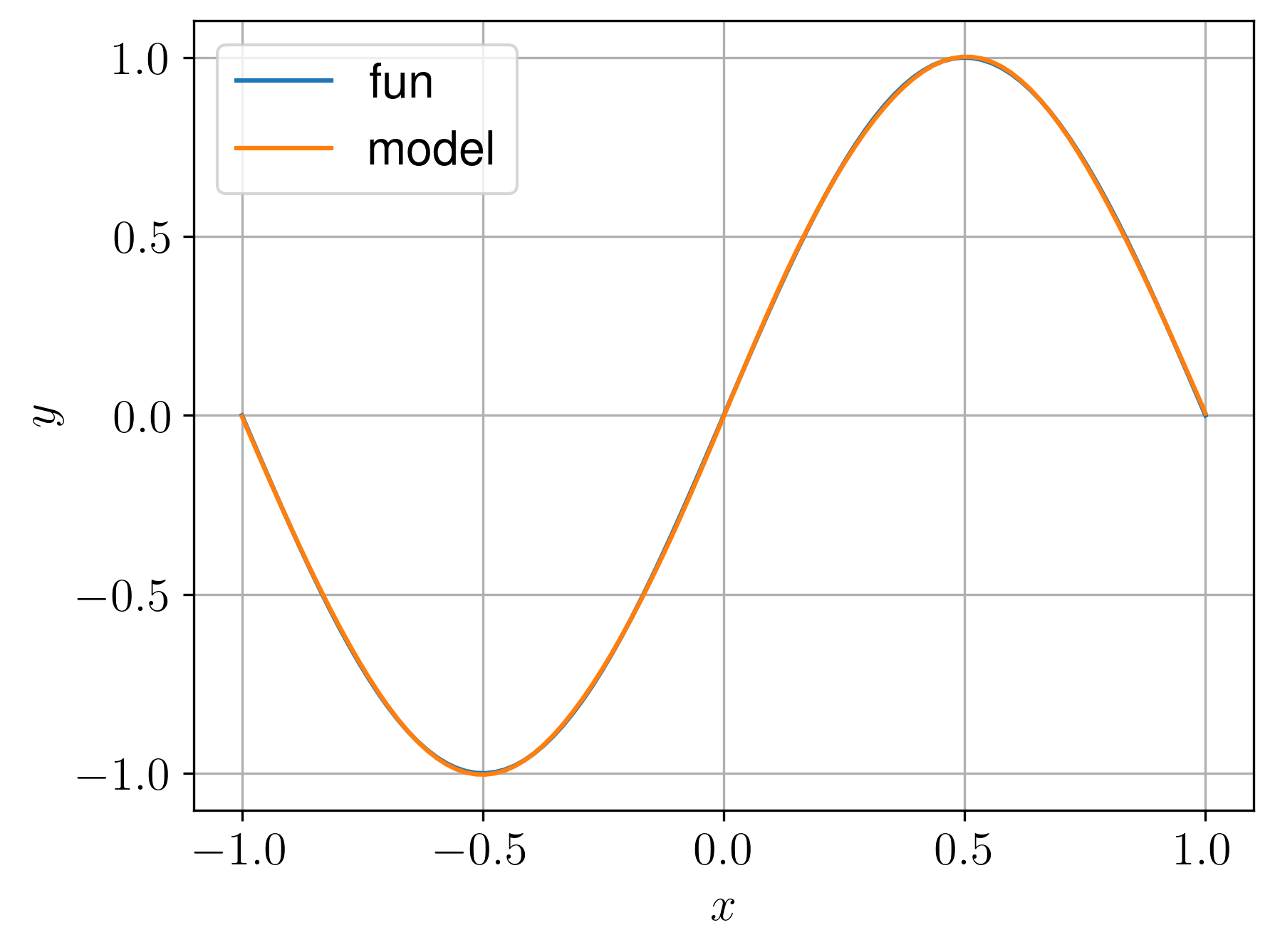
3.3.1 Função unidimensional

Vamos criar uma MLP para aproximar a função

y=\operatorname{sen}(\pi x),

(3.14)

para $x\in[-1,1]$ .

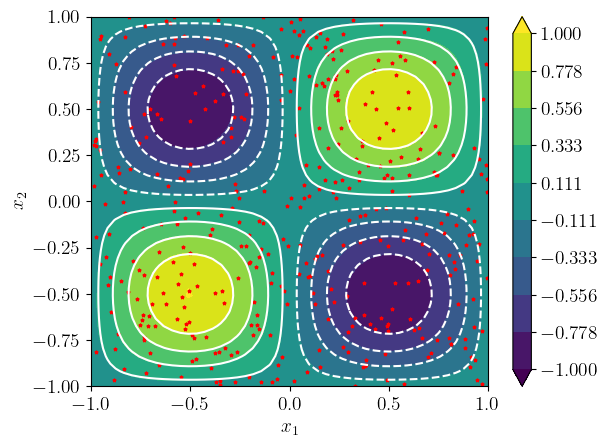
Refer to caption — Figura 3.4: Aproximação da MLP da função $y=\operatorname{sen}(\pi x)$ .

Código 8: mlp_apfun_1d

⬇

1import torch

2import matplotlib.pyplot as plt

4# modelo

6model = torch.nn.Sequential()

7model.add_module('layer_1', torch.nn.Linear(1,25))

8model.add_module('fun_1', torch.nn.Tanh())

9model.add_module('layer_2', torch.nn.Linear(25,25))

10model.add_module('fun_2', torch.nn.Tanh())

11model.add_module('layer_3', torch.nn.Linear(25,1))

13# treinamento

15## fun obj

16fun = lambda x: torch.sin(torch.pi*x)

17a = -1.

18b = 1.

20## optimizador

21optim = torch.optim.SGD(model.parameters(),

22 lr=1e-1, momentum=0.9)

24## num de amostras por época

25ns = 100

26## num max épocas

27nepochs = 5000

28## tolerância

29tol = 1e-5

31## amostras de validação

32X_val = torch.linspace(a, b, steps=100).reshape(-1,1)

33y_vest = fun(X_val)

35for epoch in range(nepochs):

37 # amostras

38 X_train = (a - b) * torch.rand((ns,1)) + b

39 y_train = fun(X_train)

41 # forward

42 y_est = model(X_train)

44 # erro

45 loss = torch.mean((y_est - y_train)**2)

47 print(f'{epoch}: {loss.item():.4e}')

49 # backward

50 optim.zero_grad()

51 loss.backward()

52 optim.step()

54 # validação

55 y_val = model(X_val)

56 loss_val = torch.mean((y_val - y_vest)**2)

57 print(f"\tloss_val = {loss_val.item():.4e}")

59 # critério de parada

60 if (loss_val.item() < tol):

61 break

64# verificação

65fig = plt.figure()

66ax = fig.add_subplot()

68x = torch.linspace(a, b,

69 steps=100).reshape(-1,1)

71y_esp = fun(x)

72ax.plot(x, y_esp, label='fun')

74y_est = model(x)

75ax.plot(x, y_est.detach(), label='model')

77ax.legend()

78ax.grid()

79ax.set_xlabel('x')

80ax.set_ylabel('y')

81plt.show()

3.3.2 Função bidimensional

Vamos criar uma MLP para aproximar a função bidimensional

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}y=% \operatorname{sen}(\pi x_{1})\operatorname{sen}(\pi x_{2}),

(3.15)

para $(x_{1},x_{2})\in\mathcal{D}:=[-1,1]^{2}$ .

Vamos usar uma arquitetura de rede $2-n_{n}\times 3-1$ (duas entradas, 3 camadas escondidas com $n_{n}$ neurônios e uma saída). Nas $n_{h}=3$ camadas escondidas, vamos usar a tangente hiperbólica como função de ativação.

Para o treinamento, vamos usar o erro médio quadrático como função erro

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\varepsilon=% \frac{1}{n_{s}}\sum_{s=1}^{n_{s}}|\tilde{y}^{(s)}-y^{(s)}|^{2},

(3.16)

onde, a cada época, $n_{s}$ pontos randômicos¹¹¹¹endnote: ¹¹Em uma distribuição uniforme. $\left\{\boldsymbol{x}^{(s)}\right\}\subset\mathcal{D}$ são usados para gerar o conjunto de treinamento $\left\{\left(\boldsymbol{x}^{(s)},y^{(s)}\right)\right\}_{s=1}^{n_{s}}$ .

Código 9: mlp_apfun_2d

⬇

1 import torch

3 # modelo

4 nn = 50

5 model = torch.nn.Sequential()

6 model.add_module('layer_1', torch.nn.Linear(2,nn))

7 model.add_module('fun_1', torch.nn.Tanh())

8 model.add_module('layer_2', torch.nn.Linear(nn,nn))

9 model.add_module('fun_2', torch.nn.Tanh())

10 model.add_module('layer_3', torch.nn.Linear(nn,nn))

11 model.add_module('fun_3', torch.nn.Tanh())

12 model.add_module(f'layer_4', torch.nn.Linear(nn,1))

14 # treinamento

16 ## fun obj

17 def fun(x1, x2):

18 return torch.sin(torch.pi*x1) * \

19 torch.sin(torch.pi*x2)

21 x1_a = -1.

22 x1_b = 1

24 x2_a = -1.

25 x2_b = 1.

28 ## optimizador

29 optim = torch.optim.SGD(model.parameters(),

30 lr=1e-1, momentum=0.9)

32 ## num de amostras por época

33 ns = 20

34 ## num max épocas

35 nepochs = 50000

36 ## tolerância

37 tol = 1e-4

39 ## amostras de validação

40 n_val = 50

41 x1 = torch.linspace(x1_a, x1_b, steps=n_val)

42 x2 = torch.linspace(x2_a, x2_b, steps=n_val)

43 X1_val, X2_val = torch.meshgrid(x1, x2, indexing='ij')

44 X_val = torch.hstack((X1_val.reshape(n_val**2,1),

45 X2_val.reshape(n_val**2,1)))

46 Y_vest = fun(X1_val, X2_val).reshape(-1,1)

48 for epoch in range(nepochs):

50 # amostras

51 X1 = (x1_b - x1_a) * torch.rand(ns**2, 1) + x1_a

52 X2 = (x2_b - x2_a) * torch.rand(ns**2, 1) + x2_a

53 # X1, X2 = torch.meshgrid(x1, x2, indexing='ij')

54 X_train = torch.hstack((X1, X2))

55 Y_train = fun(X1, X2).reshape(-1,1)

58 # forward

59 Y_est = model(X_train)

61 # erro

62 loss = torch.mean((Y_est - Y_train)**2)

64 if (epoch % 100 == 0):

65 print(f'{epoch}: {loss.item():.4e}')

67 # backward

68 optim.zero_grad()

69 loss.backward()

70 optim.step()

72 # validação

73 if (epoch % 100 == 0):

74 Y_val = model(X_val)

75 loss_val = torch.mean((Y_val - Y_vest)**2)

77 print(f"\tloss_val = {loss_val.item():.4e}")

79 # critério de parada

80 if (loss_val.item() < tol):

81 break

3.3.3 Exercícios

E. 3.3.1.

Crie uma MLP para aproximar a função gaussiana

y=e^{-x^{2}}

(3.17)

para $x\in[-1,1]$ .

E. 3.3.2.

Crie uma MLP para aproximar a função $y=\sin(x)$ para $x\in[-\pi,\pi]$ .

E. 3.3.3.

Crie uma MLP para aproximar a função $y=\sin(x)+\cos(x)$ para $x\in[0,2\pi]$ .

E. 3.3.4.

Crie uma MLP para aproximar a função gaussiana

z=e^{-(x^{2}+y^{2})}

(3.18)

para $(x,y)\in[-1,1]^{2}$ .

E. 3.3.5.

Crie uma MLP para aproximar a função $y=\sin(x_{1})\cos(x_{2})$ para $(x_{1},x_{2})\in[0,\pi]\times[-\pi,0]$ .

E. 3.3.6.

Crie uma MLP para aproximar a função $y=\sin(x_{1})+\cos(x_{2})$ para $(x_{1},x_{2})\in[-2\pi,2\pi]$ .

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Política de uso de dados