Política de uso de dados

Ao navegar por este site, você concorda com a política de uso de dados.

Política de uso de dados

Ao navegar por este site, você concorda com a política de uso de dados.

| | | |

Vetores

3 Produtos 3.2 Ângulo entre Vetores 3.4 Produto Vetorial

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

3.3 Projeção Ortogonal

Em revisão

Sejam dados os vetores $\vec{u}=\overrightarrow{OA}$ , $\vec{v}=\overrightarrow{OB}\neq\vec{0}$ . Seja, ainda, $P$ a interseção da reta perpendicular a $O B$ que passa pelo ponto $A$ . Observemos a Figura 3.2. Com isso, definimos a projeção ortogonal de $\vec{u}$ na direção de $\vec{v}$ por $\overrightarrow{OP}$ . Denotamos

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}% \overrightarrow{OP}=\operatorname{proj}_{\vec{v}}\vec{u}}.

(3.112)

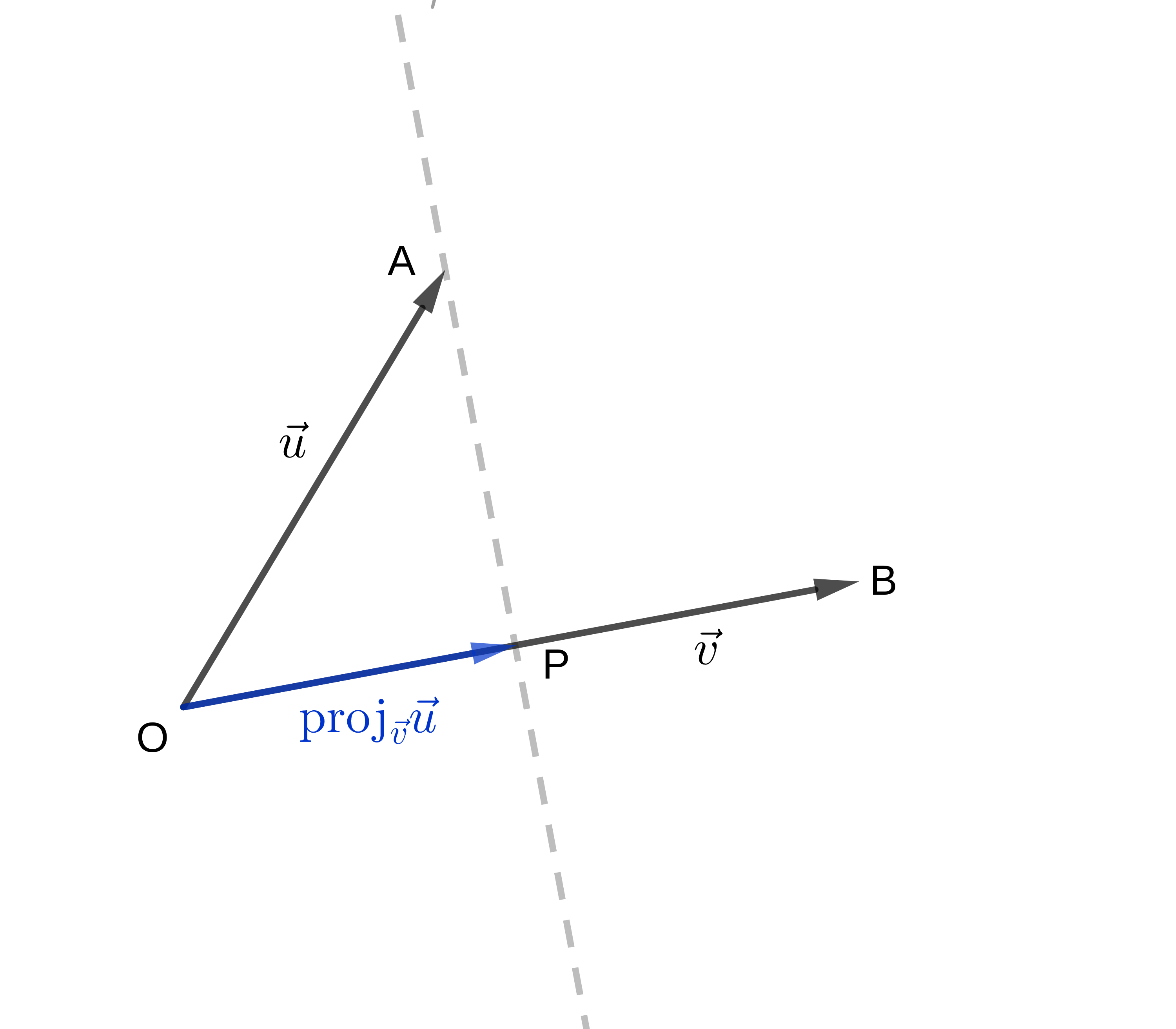
Refer to caption — Figura 3.2: Ilustração da definição da projeção ortogonal.

Da definição, temos que¹⁵¹⁵endnote: ¹⁵ $\operatorname{proj}_{\vec{v}}\vec{u}$ é um vetor múltiplo por escalar de $\vec{v}$ .

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\operatorname{% proj}_{\vec{v}}\vec{u}=\beta\cdot\vec{v}}

(3.113)

para algum número real $\beta$ . Além disso, temos

\operatorname{proj}_{\vec{v}}\vec{u}=\vec{u}+\overrightarrow{AP}.

(3.114)

Portanto

\beta\vec{v}=\vec{u}+\overrightarrow{AP}.

(3.115)

Tomando o produto escalar com $\vec{v}$ em ambos os lados desta equação, obtemos

	$\displaystyle\beta\vec{v}\cdot\vec{v}$	$\displaystyle=\vec{u}\cdot\vec{v}+\overrightarrow{AP}\cdot\vec{v}$		(3.116)
		$\displaystyle=\vec{u}\cdot\vec{v},$		(3.117)

pois $\overrightarrow{AP}\perp\vec{v}$ . Daí, lembrando que $\vec{v}\cdot\vec{v}=|v|^{2}$ , temos

\alpha=\frac{\vec{u}\cdot\vec{v}}{|\vec{v}|^{2}}

(3.118)

e concluímos que

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\operatorname{% proj}_{\vec{v}}\vec{u}=\frac{\vec{u}\cdot\vec{v}}{|\vec{v}|^{2}}\vec{v}}.

(3.119)

Exemplo 3.3.1.

Sejam $\vec{u}=(-1,1,-1)$ e $\vec{v}=(2,1,-2)$ . Usando a equação (3.119), obtemos

$\displaystyle\operatorname{proj}_{\vec{v}}\vec{u}$	$\displaystyle=\frac{(-1,1,-1)\cdot(2,1,-2)}{\|(2,1,-2)\|^{2}}(2,1,-2)$	(3.120)
	$\displaystyle=\frac{-2+1+2}{4+1+4}(2,1,-2)$	(3.121)
	$\displaystyle=\left(\frac{2}{9},\frac{1}{9},\frac{-2}{9}\right).$	(3.122)

3.3.1 Exercícios Resolvidos

ER 3.3.1.

Determine $x$ tal que a projeção de $\vec{u}=(1,x,x)$ em $\vec{v}=(1,1,0)$ tenha o dobro da norma de $\vec{v}$ .

Solução.

De (3.119), a projeção de $\vec{u}$ em $\vec{v}$ é

	$\displaystyle\operatorname{proj}_{\vec{v}}\vec{u}=\frac{\vec{u}\cdot\vec{v}}{\|% \vec{v}\|^{2}}\vec{v},$		(3.123)
	$\displaystyle\left\|\operatorname{proj}_{\vec{v}}\vec{u}\right\|=\left\|\frac{% \vec{u}\cdot\vec{v}}{\|\vec{v}\|^{2}}\right\|\|\vec{v}\|$		(3.124)
	$\displaystyle\left\|\operatorname{proj}_{\vec{v}}\vec{u}\right\|=\left\|\frac{% \vec{u}\cdot\vec{v}}{\|\vec{v}\|}\right\|$		(3.125)
	$\displaystyle\left\|\operatorname{proj}_{\vec{v}}\vec{u}\right\|=\frac{\|1+x\|}{\|% \vec{v}\|}$		(3.126)

Queremos que

\displaystyle|\operatorname{proj}_{\vec{v}}\vec{u}|=2|\vec{v}|.

(3.127)

Segue que

	$\displaystyle\frac{\|1+x\|}{\|\vec{v}\|}=2\|\vec{v}\|$		(3.128)
	$\displaystyle\|1+x\|=2\|\vec{v}\|^{2}$		(3.129)
	$\displaystyle\|1+x\|=2\cdot 2$		(3.130)
	$\displaystyle 1+x=-4\quad\text{ou}\quad 1+x=4$		(3.131)
	$\displaystyle x=-5\quad\text{ou}\quad x=3.$		(3.132)

ER 3.3.2.

Verifique que se $\vec{u}\perp\vec{v}$ , então $\operatorname{proj}_{\vec{v}}\vec{u}=\vec{0}$ . Justifique sua resposta.

Solução.

Temos que

\operatorname{proj}_{\vec{v}}\vec{u}=\frac{\vec{u}\cdot\vec{v}}{|\vec{v}|^{2}}% \vec{v}.

(3.133)

Tendo em vista que $\vec{u}\perp\vec{v}$ , temos $\vec{u}\cdot\vec{v}=0$ . Logo,

	$\displaystyle\operatorname{proj}_{\vec{v}}\vec{u}$	$\displaystyle=0\cdot\vec{v}$		(3.134)
		$\displaystyle=\vec{0}.$		(3.135)

3.3.2 Exercícios

E. 3.3.1.

Sejam $\vec{u}=(-1,1,2)$ e $\vec{v}=(1,-2,0)$ . Calcule $\operatorname{proj}_{\vec{v}}\vec{u}$ .

Resposta.

$(-3/5,6/5,0)$

E. 3.3.2.

Sejam $\vec{u}$ e $\vec{v}$ vetores unitários e seja $\alpha=\pi/6$ o ângulo entre eles. Calcule a norma da projeção ortogonal de $\vec{u}$ na direção de $\vec{v}$ .

Resposta.

$\frac{\sqrt{3}}{2}$

E. 3.3.3.

Determine $x$ tal que $\operatorname{proj}_{\vec{v}}\vec{u}=(1/6,-1/3,1/6)$ , sendo $\vec{u}=(x,1,2)$ e $\vec{v}=(1,-2,1)$ .

Resposta.

$1$

E. 3.3.4.

Verifique se a $\operatorname{proj}_{\vec{v}}\vec{u}$ tem o mesmo sentido de $\vec{v}$ para quaisquer vetores $\vec{u}$ e $\vec{v}$ dados. Justifique sua resposta.

Resposta.

Falso

E. 3.3.5.

Determine as coordenadas de todos os vetores $\vec{u}$ tais que $\operatorname{proj}_{\vec{v}}\vec{u}=\vec{v}$ , sendo que $\vec{v}=(1,0,0)$ .

Resposta.

$(1,u_{2},u_{3}),\leavevmode\nobreak\ u_{1},u_{2}\in\mathbb{R}$

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Vetores

3 Produtos 3.2 Ângulo entre Vetores 3.4 Produto Vetorial

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

3.3 Projeção Ortogonal

Em revisão

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}% \overrightarrow{OP}=\operatorname{proj}_{\vec{v}}\vec{u}}.

(3.112)

Da definição, temos que¹⁵¹⁵endnote: ¹⁵ $\operatorname{proj}_{\vec{v}}\vec{u}$ é um vetor múltiplo por escalar de $\vec{v}$ .

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\operatorname{% proj}_{\vec{v}}\vec{u}=\beta\cdot\vec{v}}

(3.113)

para algum número real $\beta$ . Além disso, temos

\operatorname{proj}_{\vec{v}}\vec{u}=\vec{u}+\overrightarrow{AP}.

(3.114)

Portanto

\beta\vec{v}=\vec{u}+\overrightarrow{AP}.

(3.115)

Tomando o produto escalar com $\vec{v}$ em ambos os lados desta equação, obtemos

	$\displaystyle\beta\vec{v}\cdot\vec{v}$	$\displaystyle=\vec{u}\cdot\vec{v}+\overrightarrow{AP}\cdot\vec{v}$		(3.116)
		$\displaystyle=\vec{u}\cdot\vec{v},$		(3.117)

pois $\overrightarrow{AP}\perp\vec{v}$ . Daí, lembrando que $\vec{v}\cdot\vec{v}=|v|^{2}$ , temos

\alpha=\frac{\vec{u}\cdot\vec{v}}{|\vec{v}|^{2}}

(3.118)

e concluímos que

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\operatorname{% proj}_{\vec{v}}\vec{u}=\frac{\vec{u}\cdot\vec{v}}{|\vec{v}|^{2}}\vec{v}}.

(3.119)

Exemplo 3.3.1.

Sejam $\vec{u}=(-1,1,-1)$ e $\vec{v}=(2,1,-2)$ . Usando a equação (3.119), obtemos

$\displaystyle\operatorname{proj}_{\vec{v}}\vec{u}$	$\displaystyle=\frac{(-1,1,-1)\cdot(2,1,-2)}{\|(2,1,-2)\|^{2}}(2,1,-2)$	(3.120)
	$\displaystyle=\frac{-2+1+2}{4+1+4}(2,1,-2)$	(3.121)
	$\displaystyle=\left(\frac{2}{9},\frac{1}{9},\frac{-2}{9}\right).$	(3.122)

3.3.1 Exercícios Resolvidos

ER 3.3.1.

Determine $x$ tal que a projeção de $\vec{u}=(1,x,x)$ em $\vec{v}=(1,1,0)$ tenha o dobro da norma de $\vec{v}$ .

Solução.

De (3.119), a projeção de $\vec{u}$ em $\vec{v}$ é

	$\displaystyle\operatorname{proj}_{\vec{v}}\vec{u}=\frac{\vec{u}\cdot\vec{v}}{\|% \vec{v}\|^{2}}\vec{v},$		(3.123)
	$\displaystyle\left\|\operatorname{proj}_{\vec{v}}\vec{u}\right\|=\left\|\frac{% \vec{u}\cdot\vec{v}}{\|\vec{v}\|^{2}}\right\|\|\vec{v}\|$		(3.124)
	$\displaystyle\left\|\operatorname{proj}_{\vec{v}}\vec{u}\right\|=\left\|\frac{% \vec{u}\cdot\vec{v}}{\|\vec{v}\|}\right\|$		(3.125)
	$\displaystyle\left\|\operatorname{proj}_{\vec{v}}\vec{u}\right\|=\frac{\|1+x\|}{\|% \vec{v}\|}$		(3.126)

Queremos que

\displaystyle|\operatorname{proj}_{\vec{v}}\vec{u}|=2|\vec{v}|.

(3.127)

Segue que

	$\displaystyle\frac{\|1+x\|}{\|\vec{v}\|}=2\|\vec{v}\|$		(3.128)
	$\displaystyle\|1+x\|=2\|\vec{v}\|^{2}$		(3.129)
	$\displaystyle\|1+x\|=2\cdot 2$		(3.130)
	$\displaystyle 1+x=-4\quad\text{ou}\quad 1+x=4$		(3.131)
	$\displaystyle x=-5\quad\text{ou}\quad x=3.$		(3.132)

ER 3.3.2.

Verifique que se $\vec{u}\perp\vec{v}$ , então $\operatorname{proj}_{\vec{v}}\vec{u}=\vec{0}$ . Justifique sua resposta.

Solução.

Temos que

\operatorname{proj}_{\vec{v}}\vec{u}=\frac{\vec{u}\cdot\vec{v}}{|\vec{v}|^{2}}% \vec{v}.

(3.133)

Tendo em vista que $\vec{u}\perp\vec{v}$ , temos $\vec{u}\cdot\vec{v}=0$ . Logo,

	$\displaystyle\operatorname{proj}_{\vec{v}}\vec{u}$	$\displaystyle=0\cdot\vec{v}$		(3.134)
		$\displaystyle=\vec{0}.$		(3.135)

3.3.2 Exercícios

E. 3.3.1.

Sejam $\vec{u}=(-1,1,2)$ e $\vec{v}=(1,-2,0)$ . Calcule $\operatorname{proj}_{\vec{v}}\vec{u}$ .

Resposta.

$(-3/5,6/5,0)$

E. 3.3.2.

Sejam $\vec{u}$ e $\vec{v}$ vetores unitários e seja $\alpha=\pi/6$ o ângulo entre eles. Calcule a norma da projeção ortogonal de $\vec{u}$ na direção de $\vec{v}$ .

Resposta.

$\frac{\sqrt{3}}{2}$

E. 3.3.3.

Determine $x$ tal que $\operatorname{proj}_{\vec{v}}\vec{u}=(1/6,-1/3,1/6)$ , sendo $\vec{u}=(x,1,2)$ e $\vec{v}=(1,-2,1)$ .

Resposta.

$1$

E. 3.3.4.

Verifique se a $\operatorname{proj}_{\vec{v}}\vec{u}$ tem o mesmo sentido de $\vec{v}$ para quaisquer vetores $\vec{u}$ e $\vec{v}$ dados. Justifique sua resposta.

Resposta.

Falso

E. 3.3.5.

Determine as coordenadas de todos os vetores $\vec{u}$ tais que $\operatorname{proj}_{\vec{v}}\vec{u}=\vec{v}$ , sendo que $\vec{v}=(1,0,0)$ .

Resposta.

$(1,u_{2},u_{3}),\leavevmode\nobreak\ u_{1},u_{2}\in\mathbb{R}$

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Pedro H A Konzen

| | | |