Política de uso de dados

Ao navegar por este site, você concorda com a política de uso de dados.

Política de uso de dados

Ao navegar por este site, você concorda com a política de uso de dados.

| | | |

Pré-Cálculo

3 Funções 3.2 Função Afim 3.4 Função Polinomial

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

3.3 Função Potência

Uma função da forma $f(x)=x^{n}$ , onde $n\neq 0$ é uma constante, é chamada de função potência.

Funções potência têm comportamentos característicos conforme o valor de $n$ . Quando $n$ é um inteiro positivo ímpar, seu domínio e sua imagem são $(-\infty,\infty)$ . Veja a Figura 3.10.

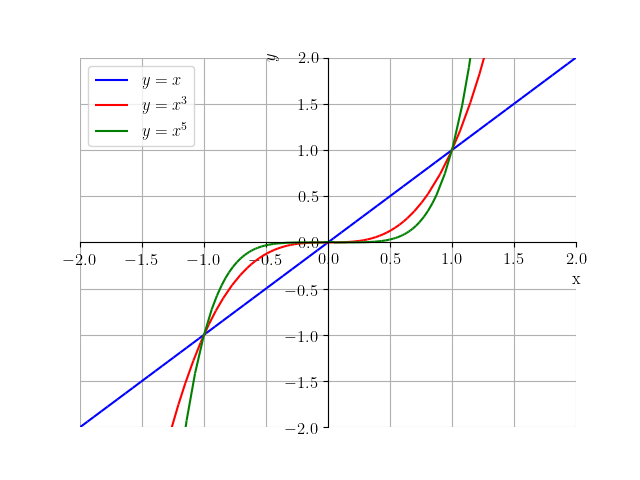
Refer to caption — Figura 3.10: Esboços dos gráficos das funções potências $y=x$ , $y=x^{3}$ e $y=x^{5}$ .

Funções potência com $n$ positivo par estão definidas em toda parte e têm imagem $[0,\infty)$ . Veja a Figura 3.11.

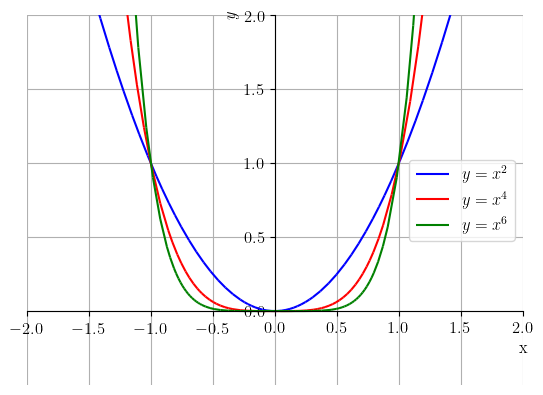
Funções potência com $n$ inteiro negativo ímpar não são definidas em $x=0$ , tendo domínio e imagem igual a $(-\infty,0)\cup(0,\infty)$ . Também, quando $n$ inteiro negativo par, a função potência não está definida em $x=0$ , tem domínio $(-\infty,0)\cup(0,\infty)$ , mas imagem $(0,\infty)$ . Veja a Figura 3.12.

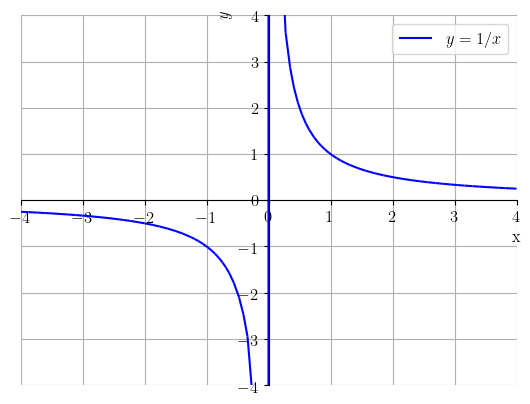
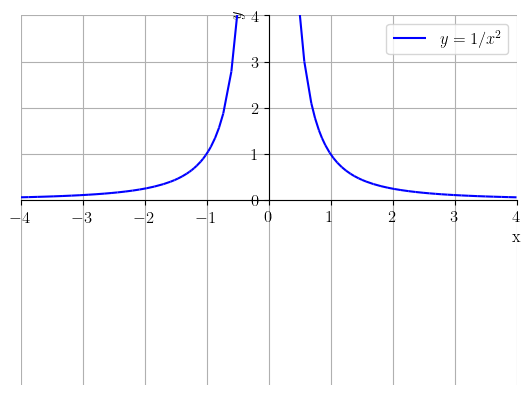
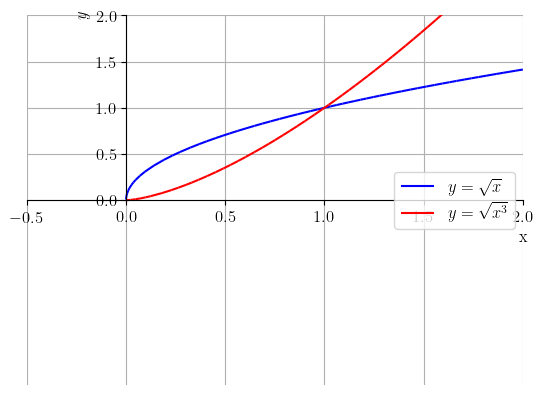
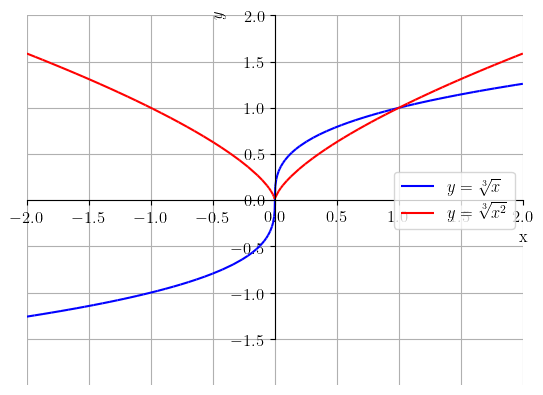
Há, ainda, comportamentos característicos quando $n=1/2$ , $1/3$ , $3/2$ e $2/3$ . Veja a Figura 3.13.

Exercícios Resolvidos

ER 3.3.1.

Determine o domínio e faça um esboço do gráfico de cada uma das seguintes funções:

a)

$\displaystyle f(x)=x^{5/2}$ ;
b)

$\displaystyle g(x)=x^{5/3}$ .

Solução.

a)

Vamos analisar a função $f(x)=x^{5/2}$ . Como $x^{5/2}=\sqrt{x^{5}}$ e não existe a raiz quadrada de número negativo, temos que $x^{5}$ deve ser não negativo. Daí, $x$ deve ser não negativo. Logo, o domínio de $f(x)=x^{5/2}$ é $[0,\infty)$ . Veja o esboço desta função na Figura 3.14.

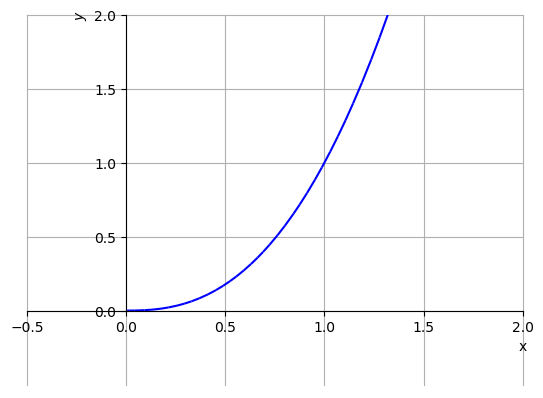
Figura 3.14: Esboço do gráfico de $f(x)=x^{5/2}$ .

Verifique o gráfico plotando-o com o SymPy!
b)

Vamos analisar a função $g(x)=x^{5/3}$ . Como $x^{5/3}=\sqrt[3]{x^{5}}$ , não temos restrição sobre os valores de $x$ . Logo, o domínio da função $g$ é $(-\infty,\infty)$ . Veja o esboço desta função na Figura 3.15.

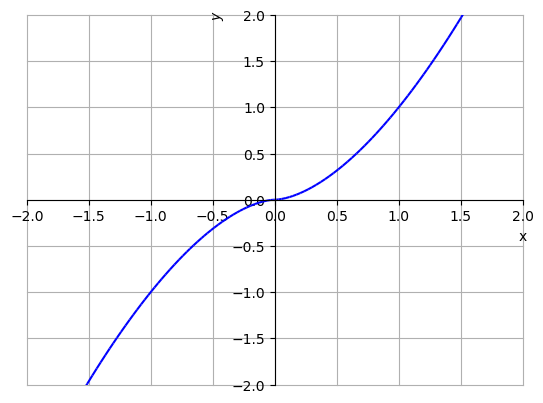
Figura 3.15: Esboço do gráfico de $g(x)=x^{5/3}$ .

Para plotar o gráfico de $g(x)$ com o SymPy, digitamos:

⬇

1 from sympy import *

2 p = plot(real_root(x**5,3),(x,-2,2))

ER 3.3.2.

Determine a equação da reta que passa pelos pontos de interseção dos gráficos das funções $f(x)=1/x$ e $g(x)=\sqrt[3]{x}$ .

Solução.

Para determinarmos a reta precisamos, antes, dos pontos de interseção. As funções se interceptam nos pontos de abscissa $x$ tais que

$\displaystyle f(x)=g(x)$	$\displaystyle\Rightarrow\frac{1}{x}=\sqrt[3]{x}$	(3.53)
	$\displaystyle\Rightarrow 1=x\sqrt[3]{x}$	(3.54)
	$\displaystyle\Rightarrow 1=x\cdot x^{\frac{1}{3}}$	(3.55)
	$\displaystyle\Rightarrow x^{1+\frac{1}{3}}=1$	(3.56)
	$\displaystyle\Rightarrow x^{\frac{4}{3}}=1$	(3.57)
	$\displaystyle\Rightarrow x^{4}=\sqrt[3]{1}$	(3.58)
	$\displaystyle\Rightarrow x^{4}=1$	(3.59)
	$\displaystyle\Rightarrow x_{0}=-1\quad\text{ou}\quad x_{1}=1.$	(3.60)

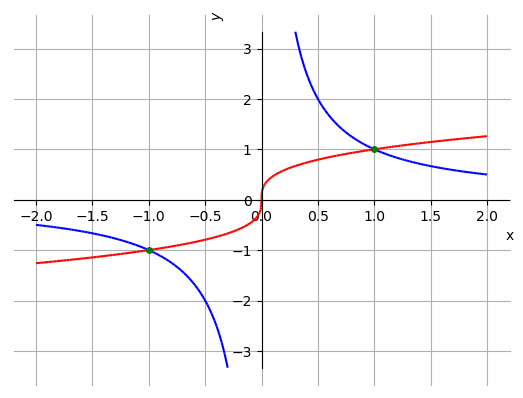
Ou seja, os gráficos se interceptam nos pontos de abscissas $x_{0}=-1$ e $x_{1}=1$ . Veja o esboço dos gráficos das funções na Figura 3.16. Agora, podemos usar qualquer uma das funções para obter as ordenadas dos pontos de interseção. Usando $f(x)$ , temos

(x_{0},y_{0})=(x_{0},f(x_{0}))=(-1,-1)

(3.61)

(x_{1},y_{1})=(x_{1},f(x_{1}))=(1,1)

(3.62)

Agora, basta determinarmos a equação da reta que passa pelos pontos $(x_{0},y_{0})=(-1,-1)$ e $(x_{1},y_{1})=(1,1)$ . De (3.41), temos que a equação da reta é tal que

	$\displaystyle y=\frac{y_{1}-y_{0}}{x_{1}-x_{0}}(x-x_{0})+y_{0}$		(3.63)
	$\displaystyle y=\frac{1-(-1)}{1-(-1)}(x-(-1))+(-1)$		(3.64)
	$\displaystyle y=x+1-1$		(3.65)
	$\displaystyle y=x.$		(3.66)

Ou seja, a que passa pelos pontos de interseção dos gráficos das funções $f(x)$ e $g(x)$ tem equação $y=x$ .

Usando o SymPy, podemos resolver o problema com o seguinte código.

⬇

1 from sympy import *

2 x = Symbol('x')

3 f = Lambda(x, 1/x)

4 g = Lambda(x, real_root(x,3))

5 # x positivo

6 x = Symbol('x', negative=True)

7 x0 = solve(f(x)-g(x))[0]

8 y0 = f(x0)

9 # x negativo

10 x = Symbol('x', positive=True)

11 x1 = solve(f(x)-g(x))[0]

12 y1 = f(x1)

14 print(f"y = {(y1-y0)/(x1-x0)*(x-x0)+y0}")

Exercícios

E. 3.3.1.

Determine o domínio, a imagem e faça um esboço do gráfico de cada uma das seguintes funções:

a)

$f(x)=x^{7}$ ;
b)

$g(x)=x^{8}$ .

Resposta.

a) domínio: $(-\infty,\infty)$ ; imagem: $(-\infty,\infty)$ . b) domínio: $(-\infty,\infty)$ ; imagem: $[0,\infty)$ . Dica: use o SymPy Gamma para verificar os esboços de seus gráficos.

E. 3.3.2.

Determine o domínio, a imagem e faça um esboço do gráfico de cada uma das seguintes funções:

a)

$\displaystyle f(x)=\frac{1}{x^{7}}$ ;
b)

$\displaystyle g(x)=\frac{1}{x^{8}}$ .

Resposta.

a) domínio: $(-\infty,\infty)\setminus\{0\}$ ; imagem: $(-\infty,\infty)\setminus\{0\}$ . b) domínio: $(-\infty,\infty)\setminus\{0\}$ ; imagem: $(0,\infty)$ . Dica: use o SymPy Gamma para verificar os esboços de seus gráficos.

E. 3.3.3.

Determine o domínio, a imagem e faça um esboço do gráfico de cada uma das seguintes funções:

a)

$\displaystyle f(x)=\sqrt{x^{2}}$ ;
b)

$\displaystyle g(x)=\sqrt[3]{x^{3}}$ .

Resposta.

a) domínio: $(-\infty,\infty)$ ; imagem: $[0,\infty)$ . b) domínio: $(-\infty,\infty)$ ; imagem: $(-\infty,\infty)$ . Dica: use o SymPy Gamma para verificar os esboços de seus gráficos.

E. 3.3.4.

Determine o(s) ponto(s) de interseção entre as funções $f(x)=x$ e $g(x)=1/x$ .

Resposta.

$(-1,-1)$ , $(1,1)$

E. 3.3.5.

Determine a equação da reta que passa pelos pontos de interseção entre as funções $f(x)=x^{2}$ e $g(x)=1/x^{2}$ .

Resposta.

$y=1$

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Pré-Cálculo

3 Funções 3.2 Função Afim 3.4 Função Polinomial

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

3.3 Função Potência

Uma função da forma $f(x)=x^{n}$ , onde $n\neq 0$ é uma constante, é chamada de função potência.

Funções potência têm comportamentos característicos conforme o valor de $n$ . Quando $n$ é um inteiro positivo ímpar, seu domínio e sua imagem são $(-\infty,\infty)$ . Veja a Figura 3.10.

Funções potência com $n$ positivo par estão definidas em toda parte e têm imagem $[0,\infty)$ . Veja a Figura 3.11.

Há, ainda, comportamentos característicos quando $n=1/2$ , $1/3$ , $3/2$ e $2/3$ . Veja a Figura 3.13.

Exercícios Resolvidos

ER 3.3.1.

Determine o domínio e faça um esboço do gráfico de cada uma das seguintes funções:

a)

$\displaystyle f(x)=x^{5/2}$ ;
b)

$\displaystyle g(x)=x^{5/3}$ .

Solução.

a)

Vamos analisar a função $f(x)=x^{5/2}$ . Como $x^{5/2}=\sqrt{x^{5}}$ e não existe a raiz quadrada de número negativo, temos que $x^{5}$ deve ser não negativo. Daí, $x$ deve ser não negativo. Logo, o domínio de $f(x)=x^{5/2}$ é $[0,\infty)$ . Veja o esboço desta função na Figura 3.14.

Figura 3.14: Esboço do gráfico de $f(x)=x^{5/2}$ .

Verifique o gráfico plotando-o com o SymPy!
b)

Vamos analisar a função $g(x)=x^{5/3}$ . Como $x^{5/3}=\sqrt[3]{x^{5}}$ , não temos restrição sobre os valores de $x$ . Logo, o domínio da função $g$ é $(-\infty,\infty)$ . Veja o esboço desta função na Figura 3.15.

Figura 3.15: Esboço do gráfico de $g(x)=x^{5/3}$ .

Para plotar o gráfico de $g(x)$ com o SymPy, digitamos:

⬇

1 from sympy import *

2 p = plot(real_root(x**5,3),(x,-2,2))

ER 3.3.2.

Determine a equação da reta que passa pelos pontos de interseção dos gráficos das funções $f(x)=1/x$ e $g(x)=\sqrt[3]{x}$ .

Solução.

Para determinarmos a reta precisamos, antes, dos pontos de interseção. As funções se interceptam nos pontos de abscissa $x$ tais que

$\displaystyle f(x)=g(x)$	$\displaystyle\Rightarrow\frac{1}{x}=\sqrt[3]{x}$	(3.53)
	$\displaystyle\Rightarrow 1=x\sqrt[3]{x}$	(3.54)
	$\displaystyle\Rightarrow 1=x\cdot x^{\frac{1}{3}}$	(3.55)
	$\displaystyle\Rightarrow x^{1+\frac{1}{3}}=1$	(3.56)
	$\displaystyle\Rightarrow x^{\frac{4}{3}}=1$	(3.57)
	$\displaystyle\Rightarrow x^{4}=\sqrt[3]{1}$	(3.58)
	$\displaystyle\Rightarrow x^{4}=1$	(3.59)
	$\displaystyle\Rightarrow x_{0}=-1\quad\text{ou}\quad x_{1}=1.$	(3.60)

(x_{0},y_{0})=(x_{0},f(x_{0}))=(-1,-1)

(3.61)

(x_{1},y_{1})=(x_{1},f(x_{1}))=(1,1)

(3.62)

Agora, basta determinarmos a equação da reta que passa pelos pontos $(x_{0},y_{0})=(-1,-1)$ e $(x_{1},y_{1})=(1,1)$ . De (3.41), temos que a equação da reta é tal que

	$\displaystyle y=\frac{y_{1}-y_{0}}{x_{1}-x_{0}}(x-x_{0})+y_{0}$		(3.63)
	$\displaystyle y=\frac{1-(-1)}{1-(-1)}(x-(-1))+(-1)$		(3.64)
	$\displaystyle y=x+1-1$		(3.65)
	$\displaystyle y=x.$		(3.66)

Ou seja, a que passa pelos pontos de interseção dos gráficos das funções $f(x)$ e $g(x)$ tem equação $y=x$ .

Usando o SymPy, podemos resolver o problema com o seguinte código.

⬇

1 from sympy import *

2 x = Symbol('x')

3 f = Lambda(x, 1/x)

4 g = Lambda(x, real_root(x,3))

5 # x positivo

6 x = Symbol('x', negative=True)

7 x0 = solve(f(x)-g(x))[0]

8 y0 = f(x0)

9 # x negativo

10 x = Symbol('x', positive=True)

11 x1 = solve(f(x)-g(x))[0]

12 y1 = f(x1)

14 print(f"y = {(y1-y0)/(x1-x0)*(x-x0)+y0}")

Exercícios

E. 3.3.1.

Determine o domínio, a imagem e faça um esboço do gráfico de cada uma das seguintes funções:

a)

$f(x)=x^{7}$ ;
b)

$g(x)=x^{8}$ .

Resposta.

a) domínio: $(-\infty,\infty)$ ; imagem: $(-\infty,\infty)$ . b) domínio: $(-\infty,\infty)$ ; imagem: $[0,\infty)$ . Dica: use o SymPy Gamma para verificar os esboços de seus gráficos.

E. 3.3.2.

Determine o domínio, a imagem e faça um esboço do gráfico de cada uma das seguintes funções:

a)

$\displaystyle f(x)=\frac{1}{x^{7}}$ ;
b)

$\displaystyle g(x)=\frac{1}{x^{8}}$ .

Resposta.

E. 3.3.3.

Determine o domínio, a imagem e faça um esboço do gráfico de cada uma das seguintes funções:

a)

$\displaystyle f(x)=\sqrt{x^{2}}$ ;
b)

$\displaystyle g(x)=\sqrt[3]{x^{3}}$ .

Resposta.

a) domínio: $(-\infty,\infty)$ ; imagem: $[0,\infty)$ . b) domínio: $(-\infty,\infty)$ ; imagem: $(-\infty,\infty)$ . Dica: use o SymPy Gamma para verificar os esboços de seus gráficos.

E. 3.3.4.

Determine o(s) ponto(s) de interseção entre as funções $f(x)=x$ e $g(x)=1/x$ .

Resposta.

$(-1,-1)$ , $(1,1)$

E. 3.3.5.

Determine a equação da reta que passa pelos pontos de interseção entre as funções $f(x)=x^{2}$ e $g(x)=1/x^{2}$ .

Resposta.

$y=1$

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Pedro H A Konzen

| | | |