Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Pré-Cálculo
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
3.1 Definição e Gráfico de Funções
3.1.1 Definição
Uma função de um conjunto em um conjunto é uma regra que associa um único elemento a cada dado elemento . Costumeiramente, identificamos uma função por uma letra, por exemplo, e escrevemos
| (3.1) |
para denotar que a função recebe valor de entrada em e fornece valor de saída em , seguindo uma regra de associação preestabelecida . Usualmente, é chamado é conjunto de entrada e de conjunto de saída.
Observação 3.1.1.
Exemplo 3.1.1.
Consultemos os seguintes exemplos:
-
a)
,
A função toma valor de entrada no conjunto dos números reais e fornece o valor de saída , também no conjunto dos números reais . A regra de associação é . Seguem alguns exemplos de aplicação:
(3.2) (3.3) (3.4) (3.5) No Python, podemos definir esta função com o seguinte código
Com isso, temos
1 In : f(x)2 Out: 2*x - 134 In : f(-1)5 Out: -367 In : f(sqrt(2))8 Out: -1 + 2*sqrt(2)910 In : z = Symbol('z', real=True)11 In : f(z)12 Out: 2*z - 1 -
b)
,
A função toma um valor de entrada em e fornece o valor de saída no conjunto dos números racionais . A regra de associação é . Segue alguns exemplos de aplicação:
(3.6) (3.7) (3.8)
Observação 3.1.2.
Ao longo do texto, vamos assumir que as funções são definidas de , salvo explicitamente escrito diferente. Assim sendo, vamos passar a usar a notação simplificada
| (3.9) |
Mais ainda, as funções serão descritas diretamente de suas regras associação.
3.1.2 Domínio e Imagem
O conjunto de todos os possíveis valores de entrada da função é chamado de domínio. Em notação de conjunto, escrevemos
| (3.10) |
i.e. o domínio de , denotado por , é o conjunto de todos os valores , tal que 2121endnote: 21O valor de saída pertence ao conjunto ..
Exemplo 3.1.2.
Estudemos os seguintes casos.
-
a)
Observamos que, dado qualquer valor de entrada , está definido e é, também, um número real. Desta forma, a função está definida para todo , i.e.
(3.11) Neste caso, dizemos que está definida em toda parte.
-
b)
:
Lembramos que a divisão por zero não está definida. A expressão está definida para todo número real não nulo, i.e. . Logo, o domínio de é
(3.12) Equivalentemente, escrevemos que está definida para todo , ou ainda, simplesmente para todo .
-
c)
A partir da regra, entendemos que é função de , i.e. . Aqui, observamos que a raiz quadrada está definida apenas para números reais não negativos. Logo, esta função está definida para tal que
(3.13) (3.14) (3.15) (3.16) Concluímos que seu domínio é .
Dada uma função , o conjunto de todos os valores tal que é chamado de imagem da função. Em notação de conjunto, temos
| (3.17) |
i.e. o conjunto de todos os valores tal que e .
Exemplo 3.1.3.
Estudemos os seguintes casos.
-
a)
:
Observamos que para qualquer número real , temos . Além disso, para cada número real não negativo , temos que
(3.18) (3.19) (3.20) Logo, concluímos que a imagem de é
(3.21) i.e. o conjunto de todos os .
-
b)
:
Primeiramente, observemos que se , então não existe número real tal que . Ou seja, não pertence a imagem desta função. Por outro lado, dado qualquer número , temos que
(3.22) (3.23) Logo, concluímos que a imagem desta função é o conjunto de todos os números reais não nulos, i.e. .
-
c)
:
No Exemplo 3.1.2, vimos que esta função está definida apenas para . Desta forma, temos que
(3.24) (3.25) Ou seja, a imagem desta função é o intervalo .
Observação 3.1.4.
Em aplicações, o domínio e imagem de funções também ficam restritos à modelagem do problema. Por exemplo, pela Lei geral dos gases, o produto da pressão pelo volume de uma gás é função da temperatura como segue
| (3.26) |
onde é o volume dado do gás e é uma constante que depende do gás. A temperatura é dada em Kelvin, logo . Entendendo a pressão como função de , temos que o domínio é , onde é a menor temperatura que o gás admite e é a maior temperatura que o gás admite. A imagem é, então, .
3.1.3 Gráfico
O gráfico de uma função é o conjunto dos pontos ou pares ordenados tal que pertence ao domínio da função. Mais precisamente, para uma função , o gráfico é o conjunto
| (3.27) |
O esboço do gráfico de uma função é, costumeiramente, uma representação geométrica dos pontos de seu gráfico em um plano cartesiano.
Exemplo 3.1.4.
Na sequência, temos os esboços dos gráficos de funções selecionadas.
-
a)
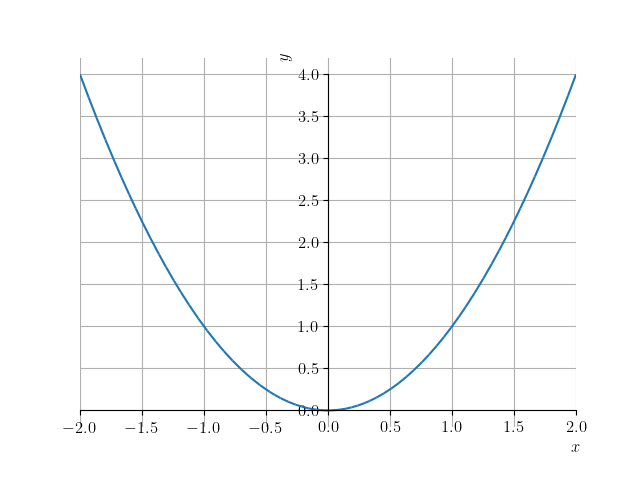
Figura 3.1: Esboço do gráfico de . -
b)
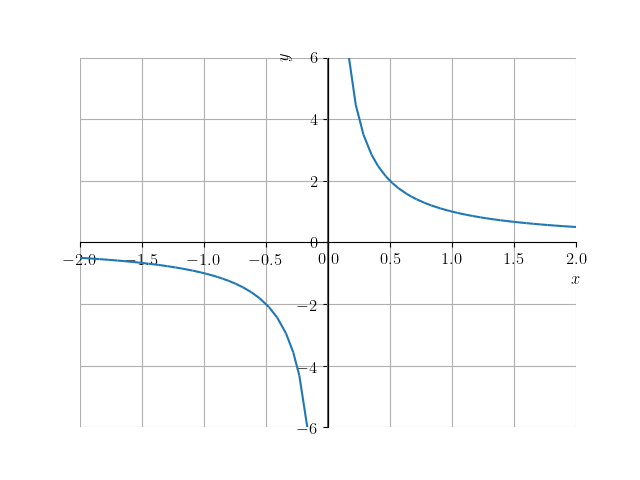
Figura 3.2: Esboço do gráfico de . -
c)
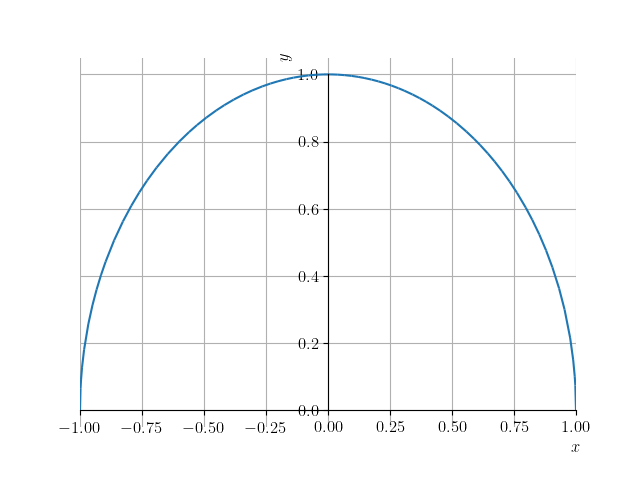
Figura 3.3: Esboço do gráfico de .
3.1.4 Categorias de Funções
Funções Algébricas
Funções algébricas são funções definidas a partir de somas, subtrações, multiplicações, divisões ou extração de raízes de funções polinomiais. Funções polinomiais e as funções algébricas derivadas são estudas nas próximas seções.
Exemplo 3.1.5.
São exemplos de funções algébrigas:
-
a)
-
b)
-
c)
-
d)
-
e)
Funções Transcendentes
Funções transcendentes são funções que não são algébricas. Como exemplos, temos as funções trigonométricas, exponencial e logarítmica, as quais são introduzidas nas próximas seções.
Exemplo 3.1.6.
São exemplos de funções transcendentes:
-
a)
-
b)
-
c)
-
d)
Funções Definidas por Partes
Funções definidas por partes são funções definidas por diferentes expressões matemáticas em diferentes partes de seu domínio.
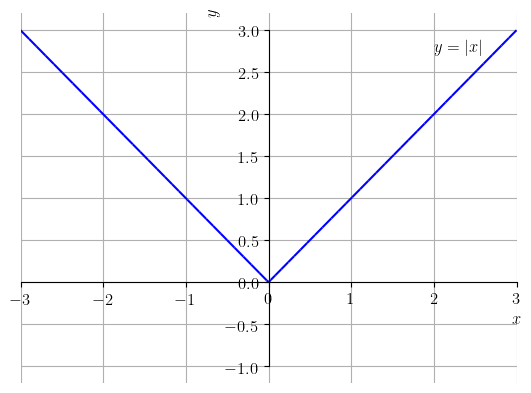
Um exemplo fundamental de função definida por partes é a função valor absoluto2222endnote: 22Esta função também pode ser definida por .
| (3.28) |
Vejamos o esboço do seu gráfico dado na Figura 3.4.
Exercícios
E. 3.1.1.
Determine o domínio e a imagem da função identidade, i.e. . Então, faça o esboço de seu gráfico.
Resposta 0.
Domínio: ; Imagem:
E. 3.1.2.
Determine o domínio e a imagem da função . Então, faça o esboço de seu gráfico.
Resposta 0.
Domínio: ; Imagem: .
E. 3.1.3.
Determine o domínio e a imagem da função . Então, faça o esboço de seu gráfico.
Resposta 0.
Domínio: ; Imagem: .
E. 3.1.4.
Determine o domínio e a imagem da função
| (3.29) |
Então, faça o esboço de seu gráfico.
Resposta 0.
Domínio: ; Imagem: .
E. 3.1.5.
Determine o domínio e a imagem da função valor absoluto.
Resposta 0.
Domínio: ; Imagem: .
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.
Pré-Cálculo
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
3.1 Definição e Gráfico de Funções
3.1.1 Definição
Uma função de um conjunto em um conjunto é uma regra que associa um único elemento a cada dado elemento . Costumeiramente, identificamos uma função por uma letra, por exemplo, e escrevemos
| (3.1) |
para denotar que a função recebe valor de entrada em e fornece valor de saída em , seguindo uma regra de associação preestabelecida . Usualmente, é chamado é conjunto de entrada e de conjunto de saída.
Observação 3.1.1.
Exemplo 3.1.1.
Consultemos os seguintes exemplos:
-
a)
,
A função toma valor de entrada no conjunto dos números reais e fornece o valor de saída , também no conjunto dos números reais . A regra de associação é . Seguem alguns exemplos de aplicação:
(3.2) (3.3) (3.4) (3.5) No Python, podemos definir esta função com o seguinte código
Com isso, temos
1 In : f(x)2 Out: 2*x - 134 In : f(-1)5 Out: -367 In : f(sqrt(2))8 Out: -1 + 2*sqrt(2)910 In : z = Symbol('z', real=True)11 In : f(z)12 Out: 2*z - 1 -
b)
,
A função toma um valor de entrada em e fornece o valor de saída no conjunto dos números racionais . A regra de associação é . Segue alguns exemplos de aplicação:
(3.6) (3.7) (3.8)
Observação 3.1.2.
Ao longo do texto, vamos assumir que as funções são definidas de , salvo explicitamente escrito diferente. Assim sendo, vamos passar a usar a notação simplificada
| (3.9) |
Mais ainda, as funções serão descritas diretamente de suas regras associação.
3.1.2 Domínio e Imagem
O conjunto de todos os possíveis valores de entrada da função é chamado de domínio. Em notação de conjunto, escrevemos
| (3.10) |
i.e. o domínio de , denotado por , é o conjunto de todos os valores , tal que 2121endnote: 21O valor de saída pertence ao conjunto ..
Exemplo 3.1.2.
Estudemos os seguintes casos.
-
a)
Observamos que, dado qualquer valor de entrada , está definido e é, também, um número real. Desta forma, a função está definida para todo , i.e.
(3.11) Neste caso, dizemos que está definida em toda parte.
-
b)
:
Lembramos que a divisão por zero não está definida. A expressão está definida para todo número real não nulo, i.e. . Logo, o domínio de é
(3.12) Equivalentemente, escrevemos que está definida para todo , ou ainda, simplesmente para todo .
-
c)
A partir da regra, entendemos que é função de , i.e. . Aqui, observamos que a raiz quadrada está definida apenas para números reais não negativos. Logo, esta função está definida para tal que
(3.13) (3.14) (3.15) (3.16) Concluímos que seu domínio é .
Dada uma função , o conjunto de todos os valores tal que é chamado de imagem da função. Em notação de conjunto, temos
| (3.17) |
i.e. o conjunto de todos os valores tal que e .
Exemplo 3.1.3.
Estudemos os seguintes casos.
-
a)
:
Observamos que para qualquer número real , temos . Além disso, para cada número real não negativo , temos que
(3.18) (3.19) (3.20) Logo, concluímos que a imagem de é
(3.21) i.e. o conjunto de todos os .
-
b)
:
Primeiramente, observemos que se , então não existe número real tal que . Ou seja, não pertence a imagem desta função. Por outro lado, dado qualquer número , temos que
(3.22) (3.23) Logo, concluímos que a imagem desta função é o conjunto de todos os números reais não nulos, i.e. .
-
c)
:
No Exemplo 3.1.2, vimos que esta função está definida apenas para . Desta forma, temos que
(3.24) (3.25) Ou seja, a imagem desta função é o intervalo .
Observação 3.1.4.
Em aplicações, o domínio e imagem de funções também ficam restritos à modelagem do problema. Por exemplo, pela Lei geral dos gases, o produto da pressão pelo volume de uma gás é função da temperatura como segue
| (3.26) |
onde é o volume dado do gás e é uma constante que depende do gás. A temperatura é dada em Kelvin, logo . Entendendo a pressão como função de , temos que o domínio é , onde é a menor temperatura que o gás admite e é a maior temperatura que o gás admite. A imagem é, então, .
3.1.3 Gráfico
O gráfico de uma função é o conjunto dos pontos ou pares ordenados tal que pertence ao domínio da função. Mais precisamente, para uma função , o gráfico é o conjunto
| (3.27) |
O esboço do gráfico de uma função é, costumeiramente, uma representação geométrica dos pontos de seu gráfico em um plano cartesiano.
Exemplo 3.1.4.
Na sequência, temos os esboços dos gráficos de funções selecionadas.
-
a)

Figura 3.1: Esboço do gráfico de . -
b)

Figura 3.2: Esboço do gráfico de . -
c)

Figura 3.3: Esboço do gráfico de .
3.1.4 Categorias de Funções
Funções Algébricas
Funções algébricas são funções definidas a partir de somas, subtrações, multiplicações, divisões ou extração de raízes de funções polinomiais. Funções polinomiais e as funções algébricas derivadas são estudas nas próximas seções.
Exemplo 3.1.5.
São exemplos de funções algébrigas:
-
a)
-
b)
-
c)
-
d)
-
e)
Funções Transcendentes
Funções transcendentes são funções que não são algébricas. Como exemplos, temos as funções trigonométricas, exponencial e logarítmica, as quais são introduzidas nas próximas seções.
Exemplo 3.1.6.
São exemplos de funções transcendentes:
-
a)
-
b)
-
c)
-
d)
Funções Definidas por Partes
Funções definidas por partes são funções definidas por diferentes expressões matemáticas em diferentes partes de seu domínio.
Um exemplo fundamental de função definida por partes é a função valor absoluto2222endnote: 22Esta função também pode ser definida por .
| (3.28) |
Vejamos o esboço do seu gráfico dado na Figura 3.4.

Exercícios
E. 3.1.1.
Determine o domínio e a imagem da função identidade, i.e. . Então, faça o esboço de seu gráfico.
Resposta 0.
Domínio: ; Imagem:
E. 3.1.2.
Determine o domínio e a imagem da função . Então, faça o esboço de seu gráfico.
Resposta 0.
Domínio: ; Imagem: .
E. 3.1.3.
Determine o domínio e a imagem da função . Então, faça o esboço de seu gráfico.
Resposta 0.
Domínio: ; Imagem: .
E. 3.1.4.
Determine o domínio e a imagem da função
| (3.29) |
Então, faça o esboço de seu gráfico.
Resposta 0.
Domínio: ; Imagem: .
E. 3.1.5.
Determine o domínio e a imagem da função valor absoluto.
Resposta 0.
Domínio: ; Imagem: .
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.