Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Política de uso de dados
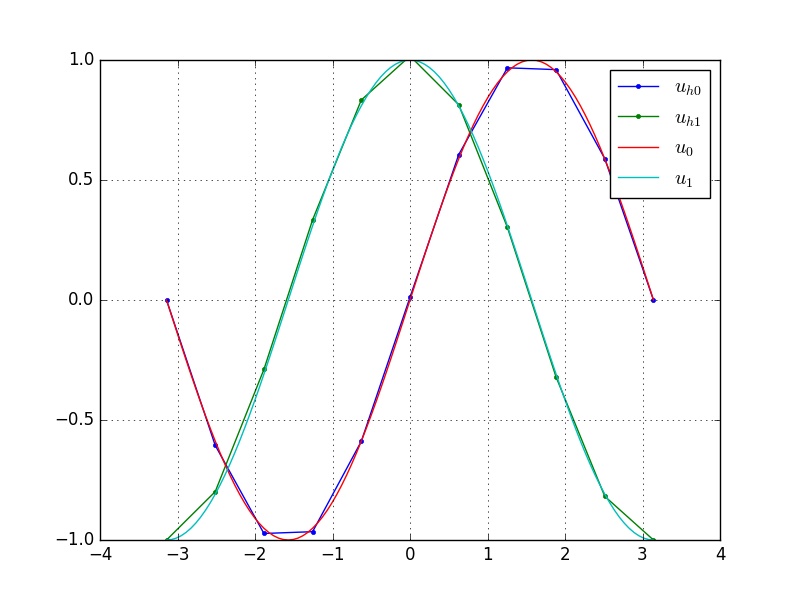
Ao navegar por este site, você concorda com a política de uso de dados.Método de Elementos Finitos
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.
Método de Elementos Finitos
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.