Política de uso de dados

Ao navegar por este site, você concorda com a política de uso de dados.

Política de uso de dados

Ao navegar por este site, você concorda com a política de uso de dados.

| | | |

Matemática Numérica I

4 Métodos para Sistemas Não Lineares 4 Métodos para Sistemas Não Lineares 4.2 Métodos Quasi-Newton

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

4.1 Método de Newton

Consideramos o problema de encontrar

\boldsymbol{x}=(x_{1},x_{2},\dotsc,x_{n})\in\mathbb{R}^{n}

(4.2)

tal que

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}F(\boldsymbol% {x})=\boldsymbol{0},

(4.3)

onde $F:\mathbb{R}^{n}\to\mathbb{R}^{n}$ é uma dada função vetorial com

F(\boldsymbol{x})=(f_{1}(\boldsymbol{x}),f_{2}(\boldsymbol{x}),\dotsc,f_{n}(% \boldsymbol{x}))\in\mathbb{R}^{n}.

(4.4)

Sejam $\boldsymbol{x}^{*}$ a solução exata de (4.3) e $\boldsymbol{x}^{(0)}$ uma dada aproximação de $\boldsymbol{x}^{*}$ . Assim sendo, tomamos a seguinte expansão de $F$ em polinômio de Taylor⁴²⁴²endnote: ⁴²Brook Taylor, 1685 - 1731, matemático britânico. Fonte: Wikipédia:Brook Taylor.:

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}F(\boldsymbol% {x}^{*})=F(\boldsymbol{x}^{(0)})+J_{F}(\boldsymbol{x}^{(0)})(\boldsymbol{x}^{*% }-\boldsymbol{x}^{(0)})+\boldsymbol{r},

(4.5)

onde $J_{F}$ é a matriz jacobiana⁴³⁴³endnote: ⁴³Carl Gustav Jakob Jacobi, 1804 - 1851, matemático alemão. Fonte: Wikipédia: Carl Gustav Jakob Jacobi. de $F$

	$\displaystyle\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% J_{F}(\boldsymbol{x})$	$\displaystyle:=\frac{\partial(f_{1},f_{2},\dotsc,f_{n})}{\partial(x_{1},x_{2},% \dotsc,x_{n})}$		(4.6)
		$\displaystyle\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% :=\begin{bmatrix}\frac{\partial f_{1}}{\partial x_{1}}&\frac{\partial f_{1}}{% \partial x_{2}}&\ldots&\frac{\partial f_{1}}{\partial x_{n}}\\ \frac{\partial f_{2}}{\partial x_{1}}&\frac{\partial f_{2}}{\partial x_{2}}&% \ldots&\frac{\partial f_{2}}{\partial x_{n}}\\ \vdots&\vdots&\vdots&\vdots\\ \frac{\partial f_{n}}{\partial x_{1}}&\frac{\partial f_{n}}{\partial x_{2}}&% \ldots&\frac{\partial f_{n}}{\partial x_{n}}\\ \end{bmatrix}$		(4.7)

e $\|\boldsymbol{r}\|^{2}\to 0$ quando $\|\boldsymbol{x}^{(0)}-\boldsymbol{x}^{*}\|\to 0$ .

Daí, como $F(\boldsymbol{x}^{*})=\boldsymbol{0}$ , segue que

J_{F}(\boldsymbol{x}^{(0)})(\boldsymbol{x}^{*}-\boldsymbol{x}^{(0)})\approx-F(% \boldsymbol{x}^{(0)}).

(4.8)

Então, multiplicando a inversa da jacobiana à esquerda, obtemos

\boldsymbol{x}^{*}-\boldsymbol{x}^{(0)}\approx-J_{F}^{-1}(\boldsymbol{x}^{(0)}% )F(\boldsymbol{x}^{(0)})

(4.9)

e, também,

\boldsymbol{x}^{*}\approx\boldsymbol{x}^{(0)}-J_{F}^{-1}(\boldsymbol{x}^{(0)})% F(\boldsymbol{x}^{(0)}).

(4.10)

O exposto acima nos motiva a iteração de Newton⁴⁴⁴⁴endnote: ⁴⁴Isaac Newton, 1642 - 1727, matemático, físico, astrônomo, teólogo e autor inglês. Fonte: Wikipédia: Isaac Newton.:


	$\displaystyle\boldsymbol{x}^{(0)}=\text{aprox. inicial},$		(4.11a)
	$\displaystyle\boldsymbol{x}^{(k+1)}=\boldsymbol{x}^{(k)}-J_{F}^{-1}(% \boldsymbol{x}^{(k)})F(\boldsymbol{x}^{(k)}),$		(4.11b)

com $k=0,1,2,\ldots$ .

Exemplo 4.1.1.

Seja o sistema de equações não lineares


	$\displaystyle x_{1}x_{2}^{2}=x_{1}^{2}x_{2}-6,$		(4.12a)
	$\displaystyle x_{1}^{2}x_{2}^{3}-7=-x_{1}.$		(4.12b)

Para usarmos o método de Newton, reescrevemos o sistema na seguinte forma


$\displaystyle x_{1}x_{2}^{2}-x_{1}^{2}x_{2}+6$	$\displaystyle=0,$	(4.13a)
$\displaystyle x_{1}+x_{1}^{2}x_{2}^{3}-7$	$\displaystyle=0.$	(4.13b)

Com isso, identificamos a função objetivo

	$\displaystyle F(\boldsymbol{x})$	$\displaystyle=\begin{bmatrix}f_{1}(\boldsymbol{x})\\ f_{2}(\boldsymbol{x})\end{bmatrix}$		(4.14)
		$\displaystyle=\begin{bmatrix}x_{1}x_{2}^{2}-x_{1}^{2}x_{2}+6\\ x_{1}+x_{1}^{2}x_{2}^{3}-7\end{bmatrix}$		(4.15)

e calculamos sua matriz jacobiana

$\displaystyle J_{F}(\boldsymbol{x})$	$\displaystyle=\frac{\partial(f_{1},f_{2})}{\partial(x_{1},x_{2})}$	(4.16)
	$\displaystyle=\begin{bmatrix}\frac{\partial f_{1}}{\partial x_{1}}&\frac{% \partial f_{1}}{\partial x_{2}}\\ \frac{\partial f_{2}}{\partial x_{1}}&\frac{\partial f_{2}}{\partial x_{2}}\\ \end{bmatrix}$	(4.17)
	$\displaystyle=\begin{bmatrix}x_{2}^{2}-2x_{1}x_{2}&2x_{1}x_{2}-x_{1}^{2}\\ 1+2x_{1}x_{2}^{3}&3x_{1}^{2}x_{2}^{2}\end{bmatrix}$	(4.18)

Definidas $F$ e $J_{F}$ e tomando a aproximação inicial

\boldsymbol{x}^{(0)}=(-1.5,1.5)

(4.19)

computamos as iterações de Newton e obtemos os resultados apresentados na Tabela 4.1.

Tabela 4.1: Resultados referentes ao Exemplo 4.1.1.

k	$\boldsymbol{x}^{(k)}$	$\\|F(\boldsymbol{x}^{(k)})\\|$
0	$(-1.50,1.50)$	$1.2\mathrm{e}\!+\!0$
1	$(-1.07,1.82)$	$1.2\mathrm{e}\!+\!0$
2	$(-9.95\mathrm{e}\!-\!1,2.00)$	$7.6\mathrm{e}\!-\!2$
3	$(-1.00,2.00)$	$1.2\mathrm{e}\!-\!4$
4	$(-1.00,2.00)$	$2.1\mathrm{e}\!-\!9$

⬇

1import numpy as np

2import numpy.linalg as npla

4def newton(F, J, x0,

5 maxiter=100, tol=1.49e-8):

6 print(f'\n{0}: x = {x0}, ' + \

7 f'norm = {npla.norm(F(x0)):.1e}')

8 info = -1

9 for k in range(maxiter):

10 x = x0 - npla.inv(J(x0))@F(x0)

11 print(f'{k+1}: x = {x}, ' + \

12 f'norm = {npla.norm(F(x)):.1e}')

13 if (npla.norm(x - x0) < tol):

14 info = 0

15 break

16 x0 = x.copy()

17 return x, info

19def F(x):

20 n = x.size

21 y = np.empty(n)

22 y[0] = x[0]*x[1]**2 - x[0]**2*x[1] + 6

23 y[1] = x[0] + x[0]**2*x[1]**3 - 7

24 return y

26def J(x):

27 n = x.size

28 y = np.empty((n,n))

29 y[0,0] = x[1]**2 - 2*x[0]*x[1]

30 y[0,1] = 2*x[0]*x[1] - x[0]**2

31 y[1,0] = 1 + 2*x[0]*x[1]**3

32 y[1,1] = 3*x[0]**2*x[1]**2

33 return y

35x0 = np.array([-1.5, 1.5])

36x, info = newton(F, J, x0)

4.1.1 Análise Numérica

Para uma função $F$ suficientemente suave e com uma escolha apropriada da aproximação inicial $\boldsymbol{x}^{(0)}$ , temos que as iterações de Newton

\boldsymbol{x}^{(k+1)}=\boldsymbol{x}^{(k)}-J_{F}^{-1}(\boldsymbol{x}^{(k)})F(% \boldsymbol{x}^{(k)}),

(4.20)

com $k=0,1,2,\ldots$ , são quadraticamente convergentes⁴⁵⁴⁵endnote: ⁴⁵Para informações mais precisas sobre a convergência do Método de Newton, consulte [8, Seção 5.3]., i.e.

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\|\boldsymbol% {x}^{(k+1)}-\boldsymbol{x}^{*}\|\leq C\|\boldsymbol{x}^{(k)}-\boldsymbol{x}^{*% }\|^{2},

(4.21)

onde $\boldsymbol{x}^{*}$ é a solução exata, i.e. $F(\boldsymbol{x}^{*})=\boldsymbol{0}$ .

Exemplo 4.1.2.

Consideremos o seguinte sistema de equações não lineares

	$\displaystyle x_{1}x_{2}^{2}-x_{1}^{2}x_{2}+6$	$\displaystyle=0,$		(4.22)
	$\displaystyle x_{1}+x_{1}^{2}x_{2}^{3}-7$	$\displaystyle=0.$		(4.23)

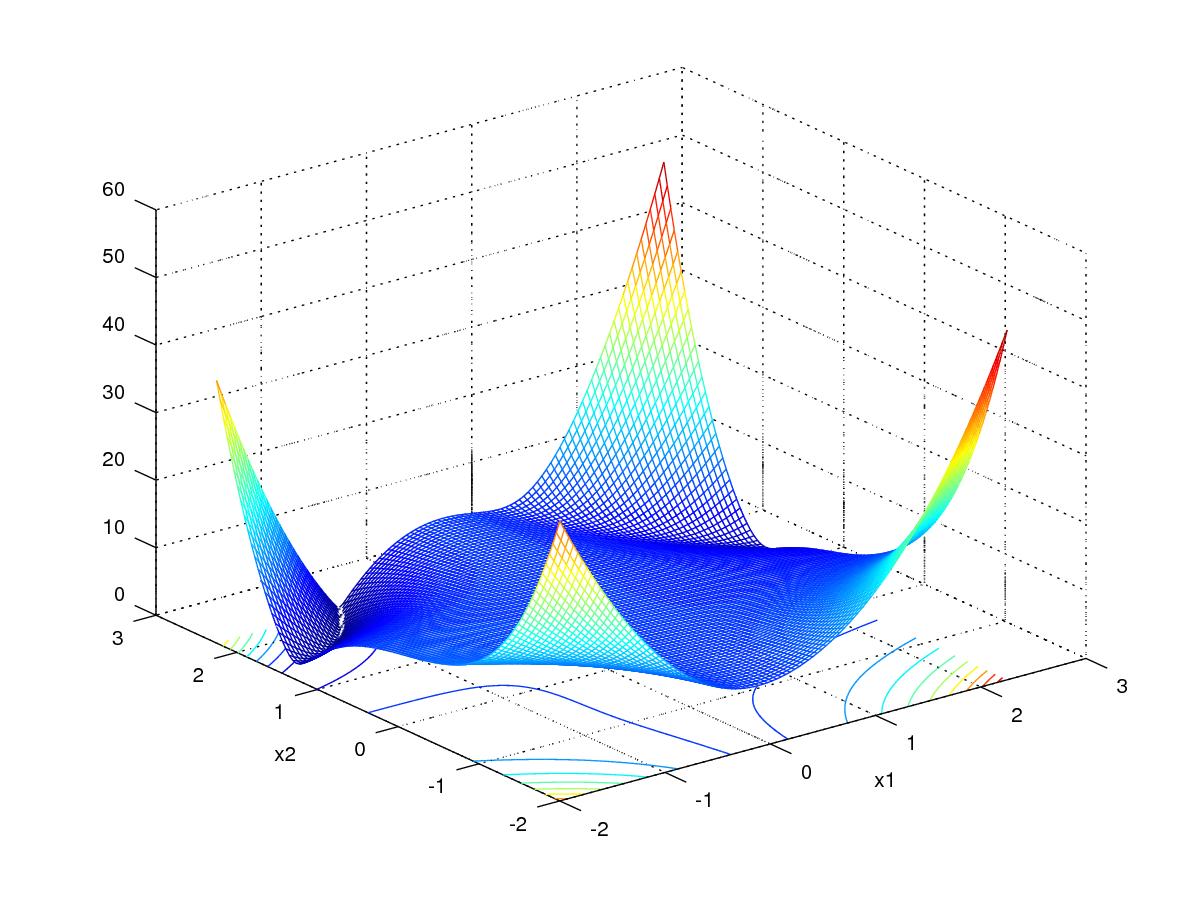
A Figura 4.1 é um esboço do gráfico da $\|F(\cdot)\|$ . Este problema foi confeccionado de forma que $\boldsymbol{x}^{*}=(-1,2)$ . Então, tomando $\boldsymbol{x}^{(0)}=(1.5,1.5)$ como aproximação inicial, computamos as iterações de Newton para este problema, donde obtemos os resultados reportados na Tabela 4.2.

Refer to caption — Figura 4.1: Esboço do gráfico de $\|F(\cdot)\|$ referente ao Exemplo 4.1.2.

k	$\boldsymbol{x}^{(k)}$	$\\|\boldsymbol{x}^{(k)}-\boldsymbol{x}^{*}\\|$
0	$(-1.50,1.50)$	$7.1\mathrm{e}\!-\!01$
1	$(-1.07,1.82)$	$2.0\mathrm{e}\!-\!01$
2	$(-9.95\mathrm{e}\!-\!1,2.00)$	$5.1\mathrm{e}\!-\!03$
3	$(-1.00,2.00)$	$2.6\mathrm{e}\!-\!05$
4	$(-1.00,2.00)$	$2.0\mathrm{e}\!-\!10$
5	$(-1.00,2.00)$	$3.1\mathrm{e}\!-\!16$

Tabela 4.2: Resultados referentes ao Exemplo 4.1.2.

4.1.2 Exercícios

E. 4.1.1.

Use o Método de Newton para computar uma solução aproximada para o sistema de equações


	$\displaystyle\frac{x_{1}^{2}}{3}+x_{2}^{2}=1$		(4.24a)
	$\displaystyle x_{1}^{2}+\frac{x_{2}^{2}}{4}=1$		(4.24b)

Resposta 0.

Soluções exatas: $\boldsymbol{x}=\pm\left(\sqrt{\frac{9}{11}},\sqrt{\frac{8}{11}}\right)$ .

E. 4.1.2.

Use o Método de Newton, com aproximação inicial $\boldsymbol{x}^{(0)}=(1.5,0.5)$ para computar uma solução aproximada para o sistema de equações


	$\displaystyle x_{1}^{2}=\cos(x_{1}x_{2})+1$		(4.25a)
	$\displaystyle\operatorname{sen}(x_{2})=2\cos(x_{1})$		(4.25b)

Resposta 0.

$\boldsymbol{x}=(1.3468109,0.4603195)$

E. 4.1.3.

Use o Método de Newton, com aproximação inicial $\boldsymbol{x}^{(0)}=(1,-1)$ para computar uma solução aproximada para o sistema de equações


	$\displaystyle 3x_{1}=\cos(x_{1}x_{2})+\frac{1}{2}$		(4.26a)
	$\displaystyle 4x_{1}^{2}+2x_{2}x_{1}=0$		(4.26b)

Resposta 0.

$\boldsymbol{x}=(4.668417\mathrm{e}\!-\!1,-9.368334\mathrm{e}\!-\!1)$

E. 4.1.4.

Use o método de Newton para obter uma aproximação de uma solução de

$\displaystyle x_{2}\operatorname{sen}(x_{3})+x_{1}-2$	$\displaystyle=0,$	(4.27)
$\displaystyle x_{1}x_{2}-\operatorname{sen}(x_{2})+0.2$	$\displaystyle=0,$	(4.28)
$\displaystyle x_{3}^{2}+\cos(x_{1}x_{2})-4.5$	$\displaystyle=0.$	(4.29)

Para tanto, use $\boldsymbol{x}^{(1)}=(1,-1,-1)$ .

Resposta 0.

$\boldsymbol{x}=(1.7519\mathrm{e}\!+\!0,-2.6202\mathrm{e}\!-\!1,-1.8983\mathrm{% e}\!+\!0)$

E. 4.1.5.

Considere o problema de encontrar os pontos de interseção no plano $x-y$ da elipse

\frac{x^{2}}{4}+\frac{y^{2}}{9}=1

(4.30)

com a curva

x=y^{2}\sqrt{x}.

(4.31)

Escreva o problema na forma $F(\boldsymbol{x})=\boldsymbol{0}$ e use o Método de Newton para encontrar o ponto de interseção próximo de $(x,y)=(1.5,1.5)$ .

Resposta 0.

$x=1.842996\mathrm{e}\!+\!0$ , $y=1.165148\mathrm{e}\!+\!0$

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Matemática Numérica I

4 Métodos para Sistemas Não Lineares 4 Métodos para Sistemas Não Lineares 4.2 Métodos Quasi-Newton

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

4.1 Método de Newton

Consideramos o problema de encontrar

\boldsymbol{x}=(x_{1},x_{2},\dotsc,x_{n})\in\mathbb{R}^{n}

(4.2)

tal que

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}F(\boldsymbol% {x})=\boldsymbol{0},

(4.3)

onde $F:\mathbb{R}^{n}\to\mathbb{R}^{n}$ é uma dada função vetorial com

F(\boldsymbol{x})=(f_{1}(\boldsymbol{x}),f_{2}(\boldsymbol{x}),\dotsc,f_{n}(% \boldsymbol{x}))\in\mathbb{R}^{n}.

(4.4)

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}F(\boldsymbol% {x}^{*})=F(\boldsymbol{x}^{(0)})+J_{F}(\boldsymbol{x}^{(0)})(\boldsymbol{x}^{*% }-\boldsymbol{x}^{(0)})+\boldsymbol{r},

(4.5)

onde $J_{F}$ é a matriz jacobiana⁴³⁴³endnote: ⁴³Carl Gustav Jakob Jacobi, 1804 - 1851, matemático alemão. Fonte: Wikipédia: Carl Gustav Jakob Jacobi. de $F$

	$\displaystyle\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% J_{F}(\boldsymbol{x})$	$\displaystyle:=\frac{\partial(f_{1},f_{2},\dotsc,f_{n})}{\partial(x_{1},x_{2},% \dotsc,x_{n})}$		(4.6)
		$\displaystyle\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% :=\begin{bmatrix}\frac{\partial f_{1}}{\partial x_{1}}&\frac{\partial f_{1}}{% \partial x_{2}}&\ldots&\frac{\partial f_{1}}{\partial x_{n}}\\ \frac{\partial f_{2}}{\partial x_{1}}&\frac{\partial f_{2}}{\partial x_{2}}&% \ldots&\frac{\partial f_{2}}{\partial x_{n}}\\ \vdots&\vdots&\vdots&\vdots\\ \frac{\partial f_{n}}{\partial x_{1}}&\frac{\partial f_{n}}{\partial x_{2}}&% \ldots&\frac{\partial f_{n}}{\partial x_{n}}\\ \end{bmatrix}$		(4.7)

e $\|\boldsymbol{r}\|^{2}\to 0$ quando $\|\boldsymbol{x}^{(0)}-\boldsymbol{x}^{*}\|\to 0$ .

Daí, como $F(\boldsymbol{x}^{*})=\boldsymbol{0}$ , segue que

J_{F}(\boldsymbol{x}^{(0)})(\boldsymbol{x}^{*}-\boldsymbol{x}^{(0)})\approx-F(% \boldsymbol{x}^{(0)}).

(4.8)

Então, multiplicando a inversa da jacobiana à esquerda, obtemos

\boldsymbol{x}^{*}-\boldsymbol{x}^{(0)}\approx-J_{F}^{-1}(\boldsymbol{x}^{(0)}% )F(\boldsymbol{x}^{(0)})

(4.9)

e, também,

\boldsymbol{x}^{*}\approx\boldsymbol{x}^{(0)}-J_{F}^{-1}(\boldsymbol{x}^{(0)})% F(\boldsymbol{x}^{(0)}).

(4.10)

O exposto acima nos motiva a iteração de Newton⁴⁴⁴⁴endnote: ⁴⁴Isaac Newton, 1642 - 1727, matemático, físico, astrônomo, teólogo e autor inglês. Fonte: Wikipédia: Isaac Newton.:


	$\displaystyle\boldsymbol{x}^{(0)}=\text{aprox. inicial},$		(4.11a)
	$\displaystyle\boldsymbol{x}^{(k+1)}=\boldsymbol{x}^{(k)}-J_{F}^{-1}(% \boldsymbol{x}^{(k)})F(\boldsymbol{x}^{(k)}),$		(4.11b)

com $k=0,1,2,\ldots$ .

Exemplo 4.1.1.

Seja o sistema de equações não lineares


	$\displaystyle x_{1}x_{2}^{2}=x_{1}^{2}x_{2}-6,$		(4.12a)
	$\displaystyle x_{1}^{2}x_{2}^{3}-7=-x_{1}.$		(4.12b)

Para usarmos o método de Newton, reescrevemos o sistema na seguinte forma


$\displaystyle x_{1}x_{2}^{2}-x_{1}^{2}x_{2}+6$	$\displaystyle=0,$	(4.13a)
$\displaystyle x_{1}+x_{1}^{2}x_{2}^{3}-7$	$\displaystyle=0.$	(4.13b)

Com isso, identificamos a função objetivo

	$\displaystyle F(\boldsymbol{x})$	$\displaystyle=\begin{bmatrix}f_{1}(\boldsymbol{x})\\ f_{2}(\boldsymbol{x})\end{bmatrix}$		(4.14)
		$\displaystyle=\begin{bmatrix}x_{1}x_{2}^{2}-x_{1}^{2}x_{2}+6\\ x_{1}+x_{1}^{2}x_{2}^{3}-7\end{bmatrix}$		(4.15)

e calculamos sua matriz jacobiana

$\displaystyle J_{F}(\boldsymbol{x})$	$\displaystyle=\frac{\partial(f_{1},f_{2})}{\partial(x_{1},x_{2})}$	(4.16)
	$\displaystyle=\begin{bmatrix}\frac{\partial f_{1}}{\partial x_{1}}&\frac{% \partial f_{1}}{\partial x_{2}}\\ \frac{\partial f_{2}}{\partial x_{1}}&\frac{\partial f_{2}}{\partial x_{2}}\\ \end{bmatrix}$	(4.17)
	$\displaystyle=\begin{bmatrix}x_{2}^{2}-2x_{1}x_{2}&2x_{1}x_{2}-x_{1}^{2}\\ 1+2x_{1}x_{2}^{3}&3x_{1}^{2}x_{2}^{2}\end{bmatrix}$	(4.18)

Definidas $F$ e $J_{F}$ e tomando a aproximação inicial

\boldsymbol{x}^{(0)}=(-1.5,1.5)

(4.19)

computamos as iterações de Newton e obtemos os resultados apresentados na Tabela 4.1.

Tabela 4.1: Resultados referentes ao Exemplo 4.1.1.

k	$\boldsymbol{x}^{(k)}$	$\\|F(\boldsymbol{x}^{(k)})\\|$
0	$(-1.50,1.50)$	$1.2\mathrm{e}\!+\!0$
1	$(-1.07,1.82)$	$1.2\mathrm{e}\!+\!0$
2	$(-9.95\mathrm{e}\!-\!1,2.00)$	$7.6\mathrm{e}\!-\!2$
3	$(-1.00,2.00)$	$1.2\mathrm{e}\!-\!4$
4	$(-1.00,2.00)$	$2.1\mathrm{e}\!-\!9$

⬇

1import numpy as np

2import numpy.linalg as npla

4def newton(F, J, x0,

5 maxiter=100, tol=1.49e-8):

6 print(f'\n{0}: x = {x0}, ' + \

7 f'norm = {npla.norm(F(x0)):.1e}')

8 info = -1

9 for k in range(maxiter):

10 x = x0 - npla.inv(J(x0))@F(x0)

11 print(f'{k+1}: x = {x}, ' + \

12 f'norm = {npla.norm(F(x)):.1e}')

13 if (npla.norm(x - x0) < tol):

14 info = 0

15 break

16 x0 = x.copy()

17 return x, info

19def F(x):

20 n = x.size

21 y = np.empty(n)

22 y[0] = x[0]*x[1]**2 - x[0]**2*x[1] + 6

23 y[1] = x[0] + x[0]**2*x[1]**3 - 7

24 return y

26def J(x):

27 n = x.size

28 y = np.empty((n,n))

29 y[0,0] = x[1]**2 - 2*x[0]*x[1]

30 y[0,1] = 2*x[0]*x[1] - x[0]**2

31 y[1,0] = 1 + 2*x[0]*x[1]**3

32 y[1,1] = 3*x[0]**2*x[1]**2

33 return y

35x0 = np.array([-1.5, 1.5])

36x, info = newton(F, J, x0)

4.1.1 Análise Numérica

Para uma função $F$ suficientemente suave e com uma escolha apropriada da aproximação inicial $\boldsymbol{x}^{(0)}$ , temos que as iterações de Newton

\boldsymbol{x}^{(k+1)}=\boldsymbol{x}^{(k)}-J_{F}^{-1}(\boldsymbol{x}^{(k)})F(% \boldsymbol{x}^{(k)}),

(4.20)

com $k=0,1,2,\ldots$ , são quadraticamente convergentes⁴⁵⁴⁵endnote: ⁴⁵Para informações mais precisas sobre a convergência do Método de Newton, consulte [8, Seção 5.3]., i.e.

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\|\boldsymbol% {x}^{(k+1)}-\boldsymbol{x}^{*}\|\leq C\|\boldsymbol{x}^{(k)}-\boldsymbol{x}^{*% }\|^{2},

(4.21)

onde $\boldsymbol{x}^{*}$ é a solução exata, i.e. $F(\boldsymbol{x}^{*})=\boldsymbol{0}$ .

Exemplo 4.1.2.

Consideremos o seguinte sistema de equações não lineares

	$\displaystyle x_{1}x_{2}^{2}-x_{1}^{2}x_{2}+6$	$\displaystyle=0,$		(4.22)
	$\displaystyle x_{1}+x_{1}^{2}x_{2}^{3}-7$	$\displaystyle=0.$		(4.23)

k	$\boldsymbol{x}^{(k)}$	$\\|\boldsymbol{x}^{(k)}-\boldsymbol{x}^{*}\\|$
0	$(-1.50,1.50)$	$7.1\mathrm{e}\!-\!01$
1	$(-1.07,1.82)$	$2.0\mathrm{e}\!-\!01$
2	$(-9.95\mathrm{e}\!-\!1,2.00)$	$5.1\mathrm{e}\!-\!03$
3	$(-1.00,2.00)$	$2.6\mathrm{e}\!-\!05$
4	$(-1.00,2.00)$	$2.0\mathrm{e}\!-\!10$
5	$(-1.00,2.00)$	$3.1\mathrm{e}\!-\!16$

Tabela 4.2: Resultados referentes ao Exemplo 4.1.2.

4.1.2 Exercícios

E. 4.1.1.

Use o Método de Newton para computar uma solução aproximada para o sistema de equações


	$\displaystyle\frac{x_{1}^{2}}{3}+x_{2}^{2}=1$		(4.24a)
	$\displaystyle x_{1}^{2}+\frac{x_{2}^{2}}{4}=1$		(4.24b)

Resposta 0.

Soluções exatas: $\boldsymbol{x}=\pm\left(\sqrt{\frac{9}{11}},\sqrt{\frac{8}{11}}\right)$ .

E. 4.1.2.

Use o Método de Newton, com aproximação inicial $\boldsymbol{x}^{(0)}=(1.5,0.5)$ para computar uma solução aproximada para o sistema de equações


	$\displaystyle x_{1}^{2}=\cos(x_{1}x_{2})+1$		(4.25a)
	$\displaystyle\operatorname{sen}(x_{2})=2\cos(x_{1})$		(4.25b)

Resposta 0.

$\boldsymbol{x}=(1.3468109,0.4603195)$

E. 4.1.3.

Use o Método de Newton, com aproximação inicial $\boldsymbol{x}^{(0)}=(1,-1)$ para computar uma solução aproximada para o sistema de equações


	$\displaystyle 3x_{1}=\cos(x_{1}x_{2})+\frac{1}{2}$		(4.26a)
	$\displaystyle 4x_{1}^{2}+2x_{2}x_{1}=0$		(4.26b)

Resposta 0.

$\boldsymbol{x}=(4.668417\mathrm{e}\!-\!1,-9.368334\mathrm{e}\!-\!1)$

E. 4.1.4.

Use o método de Newton para obter uma aproximação de uma solução de

$\displaystyle x_{2}\operatorname{sen}(x_{3})+x_{1}-2$	$\displaystyle=0,$	(4.27)
$\displaystyle x_{1}x_{2}-\operatorname{sen}(x_{2})+0.2$	$\displaystyle=0,$	(4.28)
$\displaystyle x_{3}^{2}+\cos(x_{1}x_{2})-4.5$	$\displaystyle=0.$	(4.29)

Para tanto, use $\boldsymbol{x}^{(1)}=(1,-1,-1)$ .

Resposta 0.

$\boldsymbol{x}=(1.7519\mathrm{e}\!+\!0,-2.6202\mathrm{e}\!-\!1,-1.8983\mathrm{% e}\!+\!0)$

E. 4.1.5.

Considere o problema de encontrar os pontos de interseção no plano $x-y$ da elipse

\frac{x^{2}}{4}+\frac{y^{2}}{9}=1

(4.30)

com a curva

x=y^{2}\sqrt{x}.

(4.31)

Escreva o problema na forma $F(\boldsymbol{x})=\boldsymbol{0}$ e use o Método de Newton para encontrar o ponto de interseção próximo de $(x,y)=(1.5,1.5)$ .

Resposta 0.

$x=1.842996\mathrm{e}\!+\!0$ , $y=1.165148\mathrm{e}\!+\!0$

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Pedro H A Konzen

| | | |