Política de uso de dados

Ao navegar por este site, você concorda com a política de uso de dados.

Política de uso de dados

Ao navegar por este site, você concorda com a política de uso de dados.

| | | |

Geometria Analítica

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

3.2 Hipérbole

Sejam $F_{1}$ e $F_{2}$ pontos sobre um plano $\pi$ . Sejam, também, $c$ tal que $|F_{1}F_{2}|=2c$ e $a<c$ . O lugar geométrico dos pontos $P$ tais que

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}||PF_{1}|-|PF_% {2}||=2a},

(3.34)

chama-se hipérbole. Veja Figura 3.4.

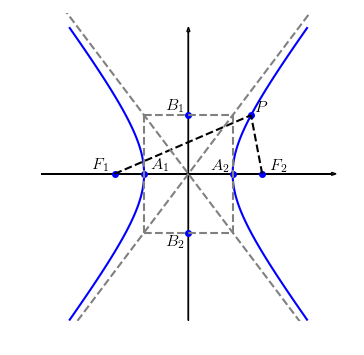
Refer to caption — Figura 3.4: Ilustração de uma hipérbole de focos $F_{1}$ e $F_{2}$ .

Os pontos $F_{1}$ e $F_{2}$ são chamados de focos da hipérbole e $2c=|F_{1}F_{2}|$ é chamada de distância focal. O ponto médio entre os pontos $F_{1}$ e $F_{2}$ é chamado de centro da hipérbole. São chamados vértices da hipérbole os pontos $A_{1}$ e $A_{2}$ , sendo que o segmento $A_{1}A_{2}$ é chamado de eixo real (ou transverso) da hipérbole. O comprimento deste eixo é $|A_{1}A_{2}|=2a$ .

Sejam $B_{1}$ e $B_{2}$ pontos $c$ distantes de $A_{1}$ e $A_{2}$ e pertencentes a reta que passa pelo centro da hipérbole e é perpendicular ao seu eixo real. O segmento $B_{1}B_{2}$ é chamado de eixo imaginário (transverso ou conjugado). Denotando $2b=|B_{1}B_{2}|$ , temos do triângulo retângulo $B_{1}OA_{1}$ que

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}c^{2}=a^{2}+b^% {2}}.

(3.35)

3.2.1 Equação reduzida da hipérbole

Assumimos um sistema de coordenadas cujo centro coincida com o centro de uma dada hipérbole e o eixo das abscissas seja coincidente com o eixo real da hipérbole. Desta forma, temos $F_{1}=(-c,0)$ e $F_{2}=(c,0)$ . Então, $P=(x,y)$ é um ponto da hipérbole quando

||PF_{1}|-|PF_{2}||=2a.

(3.36)

Daí, segue que

	$\displaystyle\|PF_{1}\|-\|PF_{2}\|=\pm 2a$		(3.37)
	$\displaystyle\sqrt{(x+c)^{2}+y^{2}}-\sqrt{(x-c)^{2}+y^{2}}=\pm 2a$		(3.38)
	$\displaystyle\sqrt{(x+c)^{2}+y^{2}}=\pm 2a+\sqrt{(x-c)^{2}+y^{2}}$		(3.39)

Elevando ao quadrado ambos os lados desta última equação, obtemos

	$\displaystyle(x+c)^{2}+y^{2}$	$\displaystyle=4a^{2}\pm 4a\sqrt{(x-c)^{2}+y^{2}}$		(3.40)
		$\displaystyle+(x-c)^{2}+y^{2}$		(3.41)

ou, equivalentemente,

	$\displaystyle x^{2}+2cx+c^{2}+y^{2}$	$\displaystyle=4a^{2}\pm 4a\sqrt{(x-c)^{2}+y^{2}}$		(3.42)
		$\displaystyle+x^{2}-2cx+c^{2}+y^{2}$		(3.43)

Simplificando e rearranjando os termos, temos

cx-a^{2}=\pm a\sqrt{(x-c)^{2}+y^{2}}).

(3.44)

Elevando novamente ao quadrado, obtemos

c^{2}x^{2}-2a^{2}cx+a^{4}=a^{2}x^{2}-2a^{2}cx+a^{2}c^{2}+a^{2}y^{2}.

(3.45)

Simplificando e rearranjando os termos, obtemos

(c^{2}-a^{2})x^{2}-a^{2}y^{2}=a^{2}(c^{2}-a^{2}).

(3.46)

Lembrando que $c^{2}=a^{2}+b^{2}$ , temos

b^{2}x^{2}-a^{2}y^{2}=a^{2}b^{2}.

(3.47)

Dividindo por $a^{2}b^{2}$ , obtemos

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\frac{x^{2}}{a% ^{2}}-\frac{y^{2}}{b^{2}}=1},

(3.48)

a qual é chamada de equação reduzida da hipérbole.

Exemplo 3.2.1.

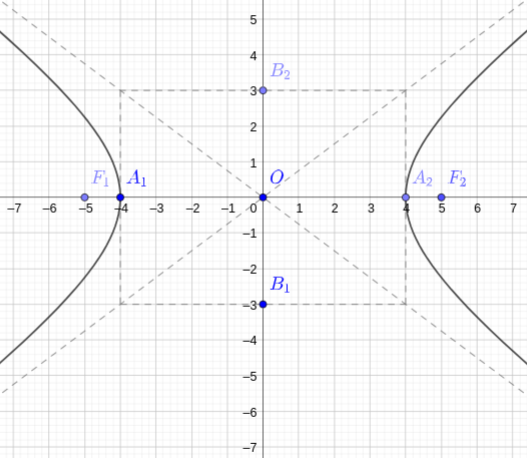
A Figura 3.5 é um esboço do gráfico da hipérbole de equação reduzida

\frac{x^{2}}{16}-\frac{y^{2}}{9}=1.

(3.49)

Exercícios resolvidos

ER 3.2.1.

Obtenha a equação reduzida da hipérbole centrada na origem e de eixo real $|A_{1}A_{2}|=8$ e eixo imaginário $|B_{1}B_{2}|=4$ .

Solução.

A equação reduzida de uma hipérbole centrada na origem tem a forma

\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1,

(3.50)

onde $2a=|A_{1}A_{2}|$ e $2b=|B_{1}B_{2}|$ . No caso deste exercício, temos

2a=8\Rightarrow a=4

(3.51)

2b=4\Rightarrow b=2

(3.52)

Logo, a equação buscada é

\frac{x^{2}}{4^{2}}-\frac{y^{2}}{2^{2}}=1

(3.53)

ou, equivalentemente,

\frac{x^{2}}{16}-\frac{y^{2}}{4}=1.

(3.54)

ER 3.2.2.

Faça o esboço da hipérbole de equação reduzida

\frac{y^{2}}{16}-\frac{x^{2}}{9}=1.

(3.55)

Solução.

Observe que nesta equação, o termo contendo $x$ tem sinal negativo e o termo contendo $y$ tem sinal positivo (compare com (3.48)). Isto nos indica que o eixo real desta hipérbole está na direção das ordenadas $O y$ e, consequentemente, o eixo imaginário na direção das abscissas $O x$ .

Da equação, temos $a^{2}=9$ e $b^{2}=16$ , donde $a=3$ e $b=4$ . Neste caso, os vértices que definem o eixo real são $A_{1}=(0,-b)=(0,-4)$ e $A_{2}=(0,b)=(0,4)$ . Os focos $F_{1}=(0,-c)$ e $F_{2}=(0,c)$ são tais que

$\displaystyle c^{2}$	$\displaystyle=a^{2}+b^{2}$	(3.56)
	$\displaystyle=9+16$	(3.57)
$\displaystyle a$	$\displaystyle=25$	(3.58)
$\displaystyle c$	$\displaystyle=5.$	(3.59)

Com estas informações, traçamos o esboço dado na Figura 3.6.

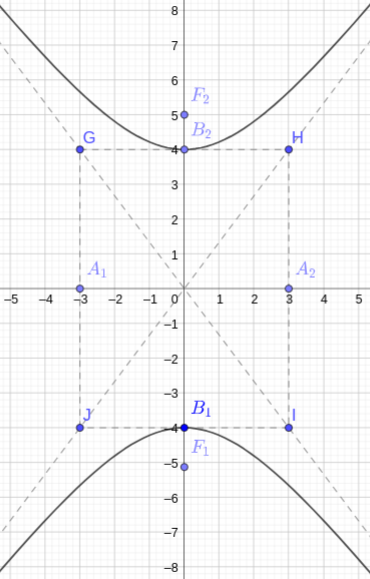
ER 3.2.3.

Mostre que uma hipérbole de equação reduzida

\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1

(3.60)

tem assíntotas

y=\pm\frac{b}{a}x.

(3.61)

Solução.

De fato, ao isolarmos $y$ na equação reduzida, obtemos

y=\pm\sqrt{\frac{b^{2}}{a^{2}}x^{2}-b^{2}}

(3.62)

Logo, para $x\to\infty$ , temos

	$\displaystyle y\to\pm\sqrt{\frac{b^{2}}{a^{2}}x^{2}}$		(3.63)
	$\displaystyle y\to\pm\sqrt{\frac{b^{2}}{a^{2}}}\sqrt{x^{2}}$		(3.64)
	$\displaystyle y\to\pm\frac{b}{a}x$		(3.65)

De forma análoga, quando $x\to-\infty$ , temos

	$\displaystyle y\to\pm\sqrt{\frac{b^{2}}{a^{2}}x^{2}}$		(3.66)
	$\displaystyle y\to\pm\sqrt{\frac{b^{2}}{a^{2}}}\sqrt{x^{2}}$		(3.67)
	$\displaystyle y\to\mp\frac{b}{a}x$		(3.68)

Ambos os resultados mostram que $\displaystyle y=\pm\frac{b}{a}x$ são assíntotas da hipérbole.

Exercícios

E. 3.2.1.

Faça o esboço da hipérbole de equação reduzida

\frac{x^{2}}{9}-\frac{y^{2}}{4}=1

(3.69)

Resposta.

E. 3.2.2.

Faça o esboço da hipérbole de equação reduzida

\frac{y^{2}}{9}-\frac{x^{2}}{4}=1

(3.70)

Resposta.

E. 3.2.3.

Determine os vértices do eixo real das seguintes hipérboles:

a)

$\displaystyle\frac{x^{2}}{9}-\frac{y^{2}}{4}=1$
b)

$\displaystyle y^{2}-\frac{x^{2}}{16}=1$

Resposta.

a) $A_{1}=(-3,0)$ , $A_{2}=(3,0)$ ; b) $B_{1}=(0,-1)$ , $B_{2}=(0,1)$

E. 3.2.4.

Determine os focos das seguintes hipérboles:

a)

$\displaystyle\frac{x^{2}}{9}-\frac{y^{2}}{4}=1$
b)

$\displaystyle y^{2}-\frac{x^{2}}{16}=1$

Resposta.

a) $F_{1}=(-\sqrt{13},0)$ , $F_{2}=(\sqrt{13},0)$ ; b) $F_{1}=(0,-\sqrt{17})$ , $F_{2}=(0,\sqrt{17})$

E. 3.2.5.

Forneça a equação reduzida da hipérbole de focos $F_{1}=(-2,0)$ , $F_{2}=(2,0)$ e de vértices do eixo real $A_{1}=(-1,0)$ e $A_{2}=(1,0)$ .

Resposta.

$\displaystyle x^{2}-\frac{y^{2}}{3}=1$

E. 3.2.6.

Forneça a equação reduzida da hipérbole de distância focal $|F_{1}F_{2}|=2\sqrt{6}$ e de vértices do eixo imaginário $A_{1}=(-2,0)$ e $A_{2}=(2,0)$ .

Resposta.

$\displaystyle\frac{y^{2}}{2}-\frac{x^{2}}{4}=1$

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Geometria Analítica

3 Cônicas 3.1 Elipse 3.3 Parábola

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

3.2 Hipérbole

Sejam $F_{1}$ e $F_{2}$ pontos sobre um plano $\pi$ . Sejam, também, $c$ tal que $|F_{1}F_{2}|=2c$ e $a<c$ . O lugar geométrico dos pontos $P$ tais que

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}||PF_{1}|-|PF_% {2}||=2a},

(3.34)

chama-se hipérbole. Veja Figura 3.4.

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}c^{2}=a^{2}+b^% {2}}.

(3.35)

3.2.1 Equação reduzida da hipérbole

||PF_{1}|-|PF_{2}||=2a.

(3.36)

Daí, segue que

	$\displaystyle\|PF_{1}\|-\|PF_{2}\|=\pm 2a$		(3.37)
	$\displaystyle\sqrt{(x+c)^{2}+y^{2}}-\sqrt{(x-c)^{2}+y^{2}}=\pm 2a$		(3.38)
	$\displaystyle\sqrt{(x+c)^{2}+y^{2}}=\pm 2a+\sqrt{(x-c)^{2}+y^{2}}$		(3.39)

Elevando ao quadrado ambos os lados desta última equação, obtemos

	$\displaystyle(x+c)^{2}+y^{2}$	$\displaystyle=4a^{2}\pm 4a\sqrt{(x-c)^{2}+y^{2}}$		(3.40)
		$\displaystyle+(x-c)^{2}+y^{2}$		(3.41)

ou, equivalentemente,

	$\displaystyle x^{2}+2cx+c^{2}+y^{2}$	$\displaystyle=4a^{2}\pm 4a\sqrt{(x-c)^{2}+y^{2}}$		(3.42)
		$\displaystyle+x^{2}-2cx+c^{2}+y^{2}$		(3.43)

Simplificando e rearranjando os termos, temos

cx-a^{2}=\pm a\sqrt{(x-c)^{2}+y^{2}}).

(3.44)

Elevando novamente ao quadrado, obtemos

c^{2}x^{2}-2a^{2}cx+a^{4}=a^{2}x^{2}-2a^{2}cx+a^{2}c^{2}+a^{2}y^{2}.

(3.45)

Simplificando e rearranjando os termos, obtemos

(c^{2}-a^{2})x^{2}-a^{2}y^{2}=a^{2}(c^{2}-a^{2}).

(3.46)

Lembrando que $c^{2}=a^{2}+b^{2}$ , temos

b^{2}x^{2}-a^{2}y^{2}=a^{2}b^{2}.

(3.47)

Dividindo por $a^{2}b^{2}$ , obtemos

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\frac{x^{2}}{a% ^{2}}-\frac{y^{2}}{b^{2}}=1},

(3.48)

a qual é chamada de equação reduzida da hipérbole.

Exemplo 3.2.1.

A Figura 3.5 é um esboço do gráfico da hipérbole de equação reduzida

\frac{x^{2}}{16}-\frac{y^{2}}{9}=1.

(3.49)

Exercícios resolvidos

ER 3.2.1.

Obtenha a equação reduzida da hipérbole centrada na origem e de eixo real $|A_{1}A_{2}|=8$ e eixo imaginário $|B_{1}B_{2}|=4$ .

Solução.

A equação reduzida de uma hipérbole centrada na origem tem a forma

\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1,

(3.50)

onde $2a=|A_{1}A_{2}|$ e $2b=|B_{1}B_{2}|$ . No caso deste exercício, temos

2a=8\Rightarrow a=4

(3.51)

2b=4\Rightarrow b=2

(3.52)

Logo, a equação buscada é

\frac{x^{2}}{4^{2}}-\frac{y^{2}}{2^{2}}=1

(3.53)

ou, equivalentemente,

\frac{x^{2}}{16}-\frac{y^{2}}{4}=1.

(3.54)

ER 3.2.2.

Faça o esboço da hipérbole de equação reduzida

\frac{y^{2}}{16}-\frac{x^{2}}{9}=1.

(3.55)

Solução.

$\displaystyle c^{2}$	$\displaystyle=a^{2}+b^{2}$	(3.56)
	$\displaystyle=9+16$	(3.57)
$\displaystyle a$	$\displaystyle=25$	(3.58)
$\displaystyle c$	$\displaystyle=5.$	(3.59)

Com estas informações, traçamos o esboço dado na Figura 3.6.

ER 3.2.3.

Mostre que uma hipérbole de equação reduzida

\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1

(3.60)

tem assíntotas

y=\pm\frac{b}{a}x.

(3.61)

Solução.

De fato, ao isolarmos $y$ na equação reduzida, obtemos

y=\pm\sqrt{\frac{b^{2}}{a^{2}}x^{2}-b^{2}}

(3.62)

Logo, para $x\to\infty$ , temos

	$\displaystyle y\to\pm\sqrt{\frac{b^{2}}{a^{2}}x^{2}}$		(3.63)
	$\displaystyle y\to\pm\sqrt{\frac{b^{2}}{a^{2}}}\sqrt{x^{2}}$		(3.64)
	$\displaystyle y\to\pm\frac{b}{a}x$		(3.65)

De forma análoga, quando $x\to-\infty$ , temos

	$\displaystyle y\to\pm\sqrt{\frac{b^{2}}{a^{2}}x^{2}}$		(3.66)
	$\displaystyle y\to\pm\sqrt{\frac{b^{2}}{a^{2}}}\sqrt{x^{2}}$		(3.67)
	$\displaystyle y\to\mp\frac{b}{a}x$		(3.68)

Ambos os resultados mostram que $\displaystyle y=\pm\frac{b}{a}x$ são assíntotas da hipérbole.

Exercícios

E. 3.2.1.

Faça o esboço da hipérbole de equação reduzida

\frac{x^{2}}{9}-\frac{y^{2}}{4}=1

(3.69)

Resposta.

E. 3.2.2.

Faça o esboço da hipérbole de equação reduzida

\frac{y^{2}}{9}-\frac{x^{2}}{4}=1

(3.70)

Resposta.

E. 3.2.3.

Determine os vértices do eixo real das seguintes hipérboles:

a)

$\displaystyle\frac{x^{2}}{9}-\frac{y^{2}}{4}=1$
b)

$\displaystyle y^{2}-\frac{x^{2}}{16}=1$

Resposta.

a) $A_{1}=(-3,0)$ , $A_{2}=(3,0)$ ; b) $B_{1}=(0,-1)$ , $B_{2}=(0,1)$

E. 3.2.4.

Determine os focos das seguintes hipérboles:

a)

$\displaystyle\frac{x^{2}}{9}-\frac{y^{2}}{4}=1$
b)

$\displaystyle y^{2}-\frac{x^{2}}{16}=1$

Resposta.

a) $F_{1}=(-\sqrt{13},0)$ , $F_{2}=(\sqrt{13},0)$ ; b) $F_{1}=(0,-\sqrt{17})$ , $F_{2}=(0,\sqrt{17})$

E. 3.2.5.

Forneça a equação reduzida da hipérbole de focos $F_{1}=(-2,0)$ , $F_{2}=(2,0)$ e de vértices do eixo real $A_{1}=(-1,0)$ e $A_{2}=(1,0)$ .

Resposta.

$\displaystyle x^{2}-\frac{y^{2}}{3}=1$

E. 3.2.6.

Forneça a equação reduzida da hipérbole de distância focal $|F_{1}F_{2}|=2\sqrt{6}$ e de vértices do eixo imaginário $A_{1}=(-2,0)$ e $A_{2}=(2,0)$ .

Resposta.

$\displaystyle\frac{y^{2}}{2}-\frac{x^{2}}{4}=1$

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Pedro H A Konzen

| | | |