Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Equações a Diferenças
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
1.1 Equações a diferenças
Equações a diferenças são aquelas que podem ser escritas na seguinte forma
| (1.1) |
onde , número natural e é função discreta (incógnita).
Exemplo 1.1.1.
Vejamos os seguintes exemplos.
-
a)
Modelo de juros compostos
(1.2) Esta equação a diferenças modela uma aplicação corrigida a juros compostos com taxa por período de tempo (dia, mês, ano, etc.). Mais especificamente, seja o valor da aplicação inicial, então
(1.3) é o valor corrigido a taxa no primeiro período (dia, mês, ano). No segundo período, o valor corrigido é
(1.4) e assim por diante.
-
b)
Equação logística
(1.5) onde representa o tamanho da população no período , é a taxa de crescimento e um limiar de saturação.
-
c)
Sequência de Fibonacci11endnote: 1Fibonacci, c. 1170 - c. 1240, matemático italiano. Fonte: Wikipedia.
(1.6) onde e .
Uma equação a diferenças (1.1) é dita ser de ordem (ou de -ésima ordem). É dita ser linear quando é função linear nas variáveis dependentes , noutro caso é dita ser não linear.
Exemplo 1.1.2.
No Exemplo 1.1.1, temos
-
a)
O modelo de juros compostos é dado por equação a diferenças de primeira ordem e linear.
-
b)
A equação logística é uma equação a diferenças de primeira ordem e não linear.
-
c)
A sequência equação de Fibonacci é descrita por uma equação a diferenças de segunda ordem e linear.
A solução de uma equação a diferenças (1.1) é uma sequência de números que satisfazem a equação.
Exemplo 1.1.3.
Vamos calcular os primeiros quatro valores da solução de
| (1.7) | |||
| (1.8) |
Para tanto, podemos fazer o seguinte procedimento iterativo. Tendo o valor inicial , temos
| (1.9) | ||||
| (1.10) | ||||
| (1.11) |
Calculado , temos
| (1.12) | ||||
| (1.13) | ||||
| (1.14) |
Então, seguimos
| (1.15) | ||||
| (1.16) | ||||
| (1.17) | ||||
| (1.18) | ||||
| (1.19) | ||||
| (1.20) |
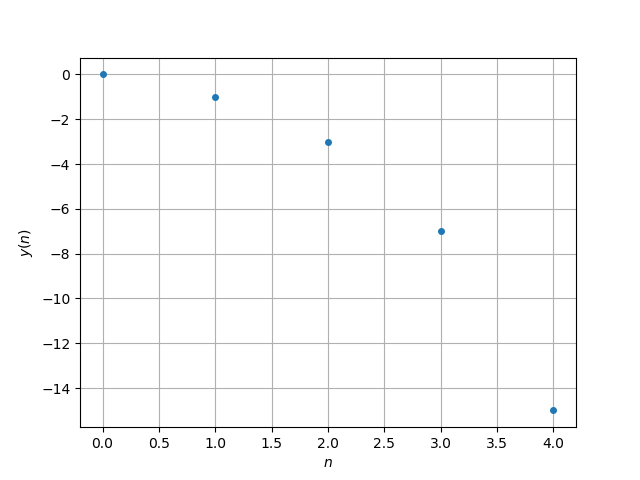
Com estes cálculos, podemos concluir que a solução da equação a diferenças é uma sequência da forma
| (1.21) |
Podemos ilustrar a solução conforme feito na figura abaixo.
Para algumas equações a diferenças, é possível escrever a solução como uma forma fechada
| (1.22) |
onde e é a função discreta que representa a solução.
Exemplo 1.1.4.
Vamos encontrar a solução para o modelo de juros compostos
| (1.23) |
A partir do valor inicial , temos
| (1.24) | ||||
| (1.25) | ||||
| (1.26) | ||||
| (1.27) | ||||
| (1.28) | ||||
| (1.29) | ||||
| (1.30) | ||||
| (1.31) |
Com isso, podemos inferir que a solução é dada por
| (1.32) |
onde o valor inicial é arbitrário.
Exercícios resolvidos
ER 1.1.1.
Calcule , sendo que
| (1.33) |
Solução 0.
Observamos que
| (1.34) | ||||
| (1.35) | ||||
| (1.36) | ||||
| (1.37) | ||||
| (1.38) | ||||
| (1.39) | ||||
| (1.40) | ||||
| (1.41) |
Com isso, temos que a solução da equação a diferenças é
| (1.42) |
Portanto,
| (1.43) | ||||
| (1.44) | ||||
| (1.45) |
ER 1.1.2.
Uma semente plantada produz uma flor com uma semente no final do primeiro ano e uma flor com duas sementes no final de cada ano consecutivo. Supondo que cada semente é plantada tão logo é produzida, escreva a equação de diferenças que modela o número de flores no final do -ésimo ano.
Solução 0.
No final do ano , o número de flores é igual a
| (1.46) |
onde é o número de flores plantadas a um ano e é o número de flores plantas há pelo menos dois anos. Ainda, temos
| (1.47) |
e
| (1.48) |
Com isso, temos
| (1.49) | ||||
| (1.50) | ||||
| (1.51) | ||||
| (1.52) | ||||
| (1.53) |
Desta forma, concluímos que o número de plantas é modelado pela seguinte equação a diferenças de segunda ordem e linear
| (1.54) |
Exercícios
E. 1.1.1.
Classifique as seguintes equações a diferenças quanto a ordem e linearidade.
-
a)
-
b)
-
c)
-
d)
-
e)
Resposta 0.
a) ordem 1, linear; b) ordem 1, linear; c) ordem 2, linear; d) ordem 1, não linear; e) ordem 2, não linear;
E. 1.1.2.
Para cada uma das seguintes equações a diferenças, calcule .
-
a)
-
b)
Resposta 0.
a) ; b)
E. 1.1.3.
Para cada uma das seguintes equações a diferenças, calcule .
-
a)
-
b)
Resposta 0.
a) ; b)
E. 1.1.4.
Encontre a equação a diferenças que modela o saldo devedor anual de uma cliente de cartão de crédito com taxa de juros de 200% a.a. (ao ano), considerando uma dívida inicial no valor de reais e que o cartão não está mais em uso.
Resposta 0.
.
E. 1.1.5.
Considere uma espécie de seres vivos monogâmicos que após um mês de vida entram na fase reprodutiva. Durante a fase reprodutiva, cada casal produz um novo casal por mês. Desconsiderando outros fatores (por exemplo, mortalidade, perda de fertilidade, etc.), encontre a equação a diferenças que modela o número de casais no -ésimo mês.
Resposta 0.
Sequência de Fibonacci
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.
Equações a Diferenças
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
1.1 Equações a diferenças
Equações a diferenças são aquelas que podem ser escritas na seguinte forma
| (1.1) |
onde , número natural e é função discreta (incógnita).
Exemplo 1.1.1.
Vejamos os seguintes exemplos.
-
a)
Modelo de juros compostos
(1.2) Esta equação a diferenças modela uma aplicação corrigida a juros compostos com taxa por período de tempo (dia, mês, ano, etc.). Mais especificamente, seja o valor da aplicação inicial, então
(1.3) é o valor corrigido a taxa no primeiro período (dia, mês, ano). No segundo período, o valor corrigido é
(1.4) e assim por diante.
-
b)
Equação logística
(1.5) onde representa o tamanho da população no período , é a taxa de crescimento e um limiar de saturação.
-
c)
Sequência de Fibonacci11endnote: 1Fibonacci, c. 1170 - c. 1240, matemático italiano. Fonte: Wikipedia.
(1.6) onde e .
Uma equação a diferenças (1.1) é dita ser de ordem (ou de -ésima ordem). É dita ser linear quando é função linear nas variáveis dependentes , noutro caso é dita ser não linear.
Exemplo 1.1.2.
No Exemplo 1.1.1, temos
-
a)
O modelo de juros compostos é dado por equação a diferenças de primeira ordem e linear.
-
b)
A equação logística é uma equação a diferenças de primeira ordem e não linear.
-
c)
A sequência equação de Fibonacci é descrita por uma equação a diferenças de segunda ordem e linear.
A solução de uma equação a diferenças (1.1) é uma sequência de números que satisfazem a equação.
Exemplo 1.1.3.
Vamos calcular os primeiros quatro valores da solução de
| (1.7) | |||
| (1.8) |
Para tanto, podemos fazer o seguinte procedimento iterativo. Tendo o valor inicial , temos
| (1.9) | ||||
| (1.10) | ||||
| (1.11) |
Calculado , temos
| (1.12) | ||||
| (1.13) | ||||
| (1.14) |
Então, seguimos
| (1.15) | ||||
| (1.16) | ||||
| (1.17) | ||||
| (1.18) | ||||
| (1.19) | ||||
| (1.20) |
Com estes cálculos, podemos concluir que a solução da equação a diferenças é uma sequência da forma
| (1.21) |
Podemos ilustrar a solução conforme feito na figura abaixo.

Para algumas equações a diferenças, é possível escrever a solução como uma forma fechada
| (1.22) |
onde e é a função discreta que representa a solução.
Exemplo 1.1.4.
Vamos encontrar a solução para o modelo de juros compostos
| (1.23) |
A partir do valor inicial , temos
| (1.24) | ||||
| (1.25) | ||||
| (1.26) | ||||
| (1.27) | ||||
| (1.28) | ||||
| (1.29) | ||||
| (1.30) | ||||
| (1.31) |
Com isso, podemos inferir que a solução é dada por
| (1.32) |
onde o valor inicial é arbitrário.
Exercícios resolvidos
ER 1.1.1.
Calcule , sendo que
| (1.33) |
Solução 0.
Observamos que
| (1.34) | ||||
| (1.35) | ||||
| (1.36) | ||||
| (1.37) | ||||
| (1.38) | ||||
| (1.39) | ||||
| (1.40) | ||||
| (1.41) |
Com isso, temos que a solução da equação a diferenças é
| (1.42) |
Portanto,
| (1.43) | ||||
| (1.44) | ||||
| (1.45) |
ER 1.1.2.
Uma semente plantada produz uma flor com uma semente no final do primeiro ano e uma flor com duas sementes no final de cada ano consecutivo. Supondo que cada semente é plantada tão logo é produzida, escreva a equação de diferenças que modela o número de flores no final do -ésimo ano.
Solução 0.
No final do ano , o número de flores é igual a
| (1.46) |
onde é o número de flores plantadas a um ano e é o número de flores plantas há pelo menos dois anos. Ainda, temos
| (1.47) |
e
| (1.48) |
Com isso, temos
| (1.49) | ||||
| (1.50) | ||||
| (1.51) | ||||
| (1.52) | ||||
| (1.53) |
Desta forma, concluímos que o número de plantas é modelado pela seguinte equação a diferenças de segunda ordem e linear
| (1.54) |
Exercícios
E. 1.1.1.
Classifique as seguintes equações a diferenças quanto a ordem e linearidade.
-
a)
-
b)
-
c)
-
d)
-
e)
Resposta 0.
a) ordem 1, linear; b) ordem 1, linear; c) ordem 2, linear; d) ordem 1, não linear; e) ordem 2, não linear;
E. 1.1.2.
Para cada uma das seguintes equações a diferenças, calcule .
-
a)
-
b)
Resposta 0.
a) ; b)
E. 1.1.3.
Para cada uma das seguintes equações a diferenças, calcule .
-
a)
-
b)
Resposta 0.
a) ; b)
E. 1.1.4.
Encontre a equação a diferenças que modela o saldo devedor anual de uma cliente de cartão de crédito com taxa de juros de 200% a.a. (ao ano), considerando uma dívida inicial no valor de reais e que o cartão não está mais em uso.
Resposta 0.
.
E. 1.1.5.
Considere uma espécie de seres vivos monogâmicos que após um mês de vida entram na fase reprodutiva. Durante a fase reprodutiva, cada casal produz um novo casal por mês. Desconsiderando outros fatores (por exemplo, mortalidade, perda de fertilidade, etc.), encontre a equação a diferenças que modela o número de casais no -ésimo mês.
Resposta 0.
Sequência de Fibonacci
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.