Política de uso de dados

Ao navegar por este site, você concorda com a política de uso de dados.

Política de uso de dados

Ao navegar por este site, você concorda com a política de uso de dados.

| | | |

Cálculo I

1 Limites 1 Limites 1.2 Regras para o cálculo de limites

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

1.1 Noção de limites

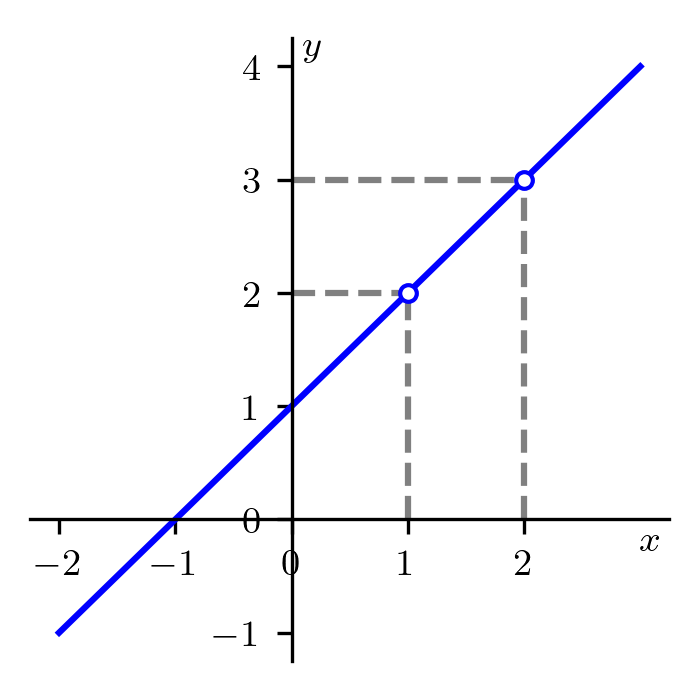
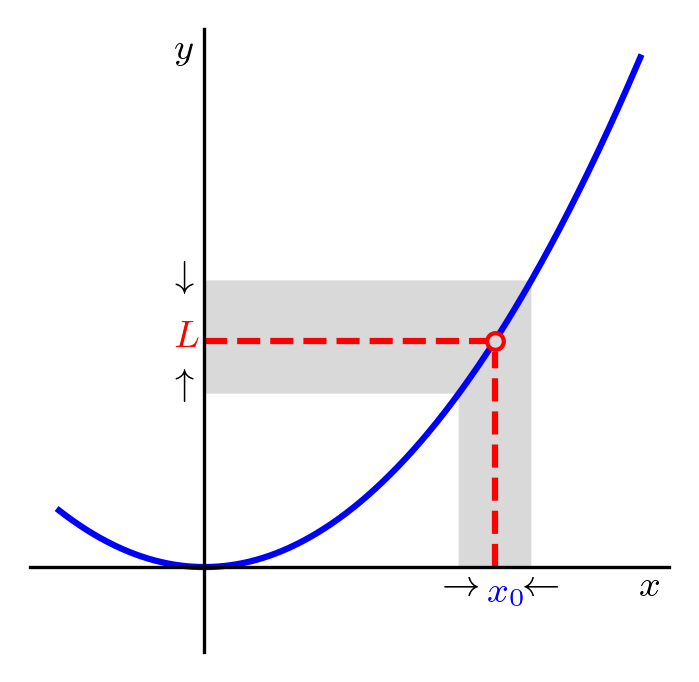
Seja $f$ uma função definida em um intervalo aberto em torno de um dado ponto $x_{0}$ , exceto talvez em $x_{0}$ . Quando o valor de $f(x)$ é arbitrariamente próximo de um número $L$ para $x$ suficientemente próximo de $x_{0}$ , escrevemos

\lim_{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}x\to x_{0}}f(x% )={\color[rgb]{1,0,0}\definecolor[named]{pgfstrokecolor}{rgb}{1,0,0}% \pgfsys@color@rgb@stroke{1}{0}{0}\pgfsys@color@rgb@fill{1}{0}{0}L}

(1.1)

e dizemos que o limite da função $f$ é $L$ quando $x$ tende a $x_{0}$ . Consultemos a Figura 1.1.

Refer to caption — Figura 1.1: Noção de limite de uma função.

Exemplo 1.1.1.

Consideremos a função

f(x)=\frac{(x^{2}-1)(x-2)}{(x-1)(x-2)}.

(1.2)

Na Figura 1.2, temos um esboço do gráfico desta função.

Vejamos os seguintes casos:

•

$\displaystyle\lim_{x\to 0}f(x)=1=f(0)$ .

$x$ $y=f(x)$

$-0,01$ $0,99$

$-0,001$ $0,999$

$-0,0001$ $0,9999$

$\downarrow$ $\downarrow$

$0$ $1$

$\uparrow$ $\uparrow$

$0,0001$ $1,0001$

$0,001$ $1,001$

$0,01$ $1,01$

Código 1: Python

⬇

1from sympy.abc import x

2from sympy import limit

3limit((x**2-1)*(x-2)/((x-1)*(x-2)), x, 0)

⬇

1
•

$\displaystyle\lim_{x\to 1}f(x)=2$ , embora $f(1)$ não esteja definido.

$x$ $f(x)$

$0,9$ $1,9$

$0,99$ $1,99$

$0,999$ $1,999$

$\downarrow$ $\downarrow$

$1$ $2$

$\uparrow$ $\uparrow$

$1,0001$ $2,0001$

$1,001$ $2,001$

$1,01$ $2,01$

Código 2: Python

⬇

1from sympy.abc import x

2from sympy import limit

3limit((x**2-1)*(x-2)/((x-1)*(x-2)), x, 1)

⬇

2
•

$\displaystyle\lim_{x\to 2}f(x)=3$ , embora $f(2)$ também não esteja definido. Verifique!

$x$	$y=f(x)$
$-0,01$	$0,99$
$-0,001$	$0,999$
$-0,0001$	$0,9999$
$\downarrow$	$\downarrow$
$0$	$1$
$\uparrow$	$\uparrow$
$0,0001$	$1,0001$
$0,001$	$1,001$
$0,01$	$1,01$

$x$	$f(x)$
$0,9$	$1,9$
$0,99$	$1,99$
$0,999$	$1,999$
$\downarrow$	$\downarrow$
$1$	$2$
$\uparrow$	$\uparrow$
$1,0001$	$2,0001$
$1,001$	$2,001$
$1,01$	$2,01$

1.1.1 Limites da função constante e da função identidade

Da noção de limite, podemos inferir que

\lim_{x\to x_{0}}k=k,

(1.3)

seja qual for a constante $k$ . Consultemos a Figura 1.3.

Exemplo 1.1.2.

Vejamos os seguintes casos:

a)

$\displaystyle\lim_{x\to-1}1=1$

Código 3: Python

⬇

1from sympy.abc import x

2from sympy import limit

3limit(1, x, -1)

⬇

1
b)

$\displaystyle\lim_{x\to 2}-3=-3$
c)

$\displaystyle\lim_{x\to\pi}\left(\sqrt{2}-e\right)=\sqrt{2}-e$

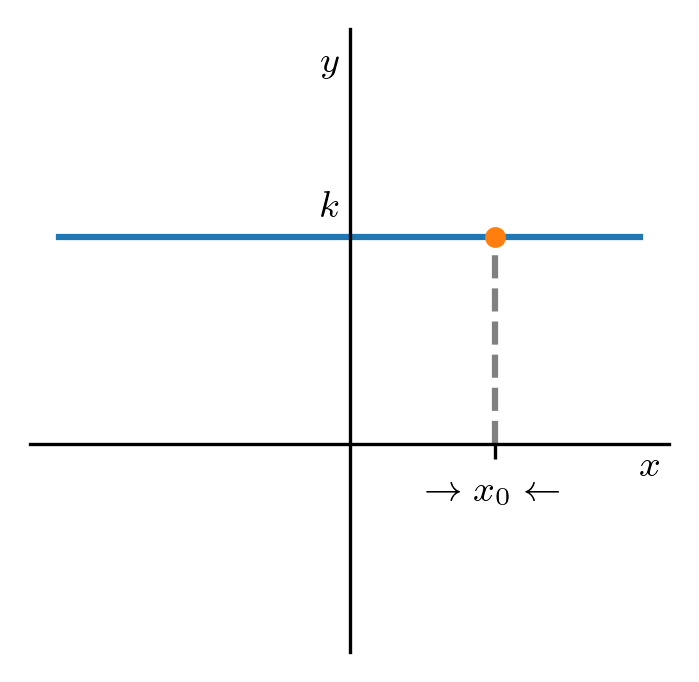
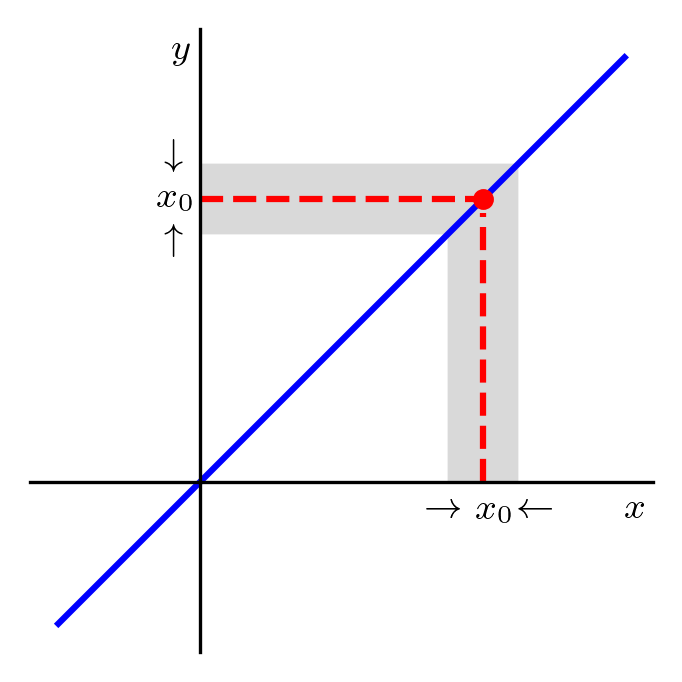
Também da noção de limites, podemos inferir que

\lim_{x\to a}x=a,

(1.4)

seja qual for o ponto $a$ . Consultemos a Figura 1.4.

Código 4: Python

⬇

1from sympy.abc import x, a

2from sympy import limit

3limit(x, x, a)

⬇

Exemplo 1.1.3.

Estudemos os seguintes casos:

a)

$\displaystyle\lim_{x\to-1}x=-1$

Código 5: Python

⬇

1from sympy.abc import x

2from sympy import limit

3limit(x, x, -1)

⬇

-1
b)

$\displaystyle\lim_{x\to 2}x=2$
c)

$\displaystyle\lim_{x\to\pi}x=\pi$

1.1.2 Exercícios resolvidos

ER 1.1.1.

Estime o valor do limite

\lim_{x\to 1}e^{x}.

(1.5)

Solução.

Da noção de limite, podemos buscar inferir o limite de uma função em um ponto $x_{0}$ , computando seus valores próximos deste ponto. Por exemplo, construímos a seguinte tabela:

$x$	f(x)
$0,9$	$2,460$
$0,99$	$2,691$
$0,999$	$2,716$
$\downarrow$	$\downarrow$
$1$	$2,72$
$\uparrow$	$\uparrow$
$1,0001$	$2,719$
$1,001$	$2,721$
$1,01$	$2,746$

Com isso, inferimos que

\lim_{x\to 1}e^{x}\approx 2,72.

(1.6)

Mais adiante, veremos que $\lim_{x\to 1}e^{x}=e\approx 2,718281828459045...$ .

Código 6: Python

⬇

1from sympy.abc import x

2from sympy import limit, exp

3L = limit(exp(x), x, 1)

4print(f'{L} =', L.evalf())

⬇

E = 2.71828182845905

ER 1.1.2.

Considere que uma dada função $f$ tenha o seguinte esboço de gráfico:

Então, infira o valores de

a)

$\displaystyle\lim_{x\to-2}f(x)$
b)

$\displaystyle\lim_{x\to-1}f(x)$
c)

$\displaystyle\lim_{x\to 1}f(x)$

Solução.

a)

$\displaystyle\lim_{x\to-2}f(x)$

Para valores suficientemente próximos de $-2$ e a direita de $-2$ (i.e. $x>-2$ ), podemos observar que $f(x)=1$ . Para tais valores de $x$ a esquerda de $-2$ (i.e. $x<-2$ ), vemos que os valores de $f(x)$ tornam-se próximos de $1$ . Isto é, temos que os valores de $f(x)$ podemos ser tomados arbitrariamente próximos de $L=1$ , se tomarmos $x$ suficientemente próximo de $-2$ . Concluímos que

$\lim_{x\to-2}=1.$ (1.7)
b)

$\displaystyle\lim_{x\to-1}f(x)$

Mesmo sendo $f(-1)=2$ , observamos que os valores de $f(x)$ podem ser tomados arbitrariamente próximos de $1$ , se escolhemos valores de $x$ suficientemente próximos de $-1$ . Logo,

$\lim_{x\to-1}f(x)=1.$ (1.8)
c)

$\displaystyle\lim_{x\to 1}f(x)$

Aqui, para valores de $x$ suficientemente próximos de $x_{0}=1$ e a esquerda ( $x<1$ ), vemos que os valores de $f(x)$ são próximos de $L=2$ . Entretanto, para valores de $x$ suficientemente próximos de $x_{0}=1$ e a direita ( $x>1$ ), temos que os valores de $f(x)$ são próximos de $L=1$ . Ou seja, não é possível escolher um valor $L$ tal que $f(x)$ esteja arbitrariamente próxima ao tomarmos $x$ suficientemente próximo de $x_{0}=1$ , pois $L$ dependerá de $x$ estar a esquerda ou a direita de do ponto $x_{0}=1$ . Concluímos que este limite não existe, e escrevemos

$\not\exists\lim_{x\to 1}f(x).$ (1.9)

1.1.3 Exercícios

E. 1.1.1.

Considere que uma dada função $f$ tenha o seguinte esboço de gráfico:

Forneça o valor dos seguintes limites:

a)

$\displaystyle\lim_{x\to-1}f(x)$
b)

$\displaystyle\lim_{x\to 1}f(x)$
c)

$\displaystyle\lim_{x\to 2}f(x)$
d)

$\displaystyle\lim_{x\to 3}f(x)$

Resposta.

a) $-1$ ; b) $-1$ ; c) $2$ ; d) $\nexists$

E. 1.1.2.

Considerando a mesma função do exercício anterior (Exercício 1.1.1), forneça

1.

$\displaystyle\lim_{x\to-\frac{3}{2}}f(x)$
2.

$\displaystyle\lim_{x\to 0}f(x)$
3.

$\displaystyle\lim_{x\to\frac{3}{4}}f(x)$

Resposta.

a) $-\frac{3}{2}$ ; b) $-1$ ; c) $-1$

E. 1.1.3.

Forneça o valor dos seguintes limites:

a)

$\displaystyle\lim_{x\to 2}2$
b)

$\displaystyle\lim_{x\to-2}2$
c)

$\displaystyle\lim_{x\to 2}-3$
d)

$\displaystyle\lim_{x\to e}\pi$

Resposta.

a) 2; b) 2; c) -3; d) $\pi$

E. 1.1.4.

Forneça o valor dos seguintes limites:

a)

$\displaystyle\lim_{x\to 2}x$
b)

$\displaystyle\lim_{x\to-2}x$
c)

$\displaystyle\lim_{x\to-3}x$
d)

$\displaystyle\lim_{x\to e}x$

Resposta.

a) 2; b) -2; c) -3; d) $e$

E. 1.1.5.

Com base na noção de limites, calcule:

a)

$\displaystyle\lim_{x\to 1}|x|$
b)

$\displaystyle\lim_{x\to-1}|x|$
c)

$\displaystyle\lim_{x\to 10^{-10}}|x|$

Resposta.

a) $1$ ; b) $1$ ; c) $10^{-10}$

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Cálculo I

1 Limites 1 Limites 1.2 Regras para o cálculo de limites

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

1.1 Noção de limites

\lim_{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}x\to x_{0}}f(x% )={\color[rgb]{1,0,0}\definecolor[named]{pgfstrokecolor}{rgb}{1,0,0}% \pgfsys@color@rgb@stroke{1}{0}{0}\pgfsys@color@rgb@fill{1}{0}{0}L}

(1.1)

e dizemos que o limite da função $f$ é $L$ quando $x$ tende a $x_{0}$ . Consultemos a Figura 1.1.

Exemplo 1.1.1.

Consideremos a função

f(x)=\frac{(x^{2}-1)(x-2)}{(x-1)(x-2)}.

(1.2)

Na Figura 1.2, temos um esboço do gráfico desta função.

Vejamos os seguintes casos:

•

$\displaystyle\lim_{x\to 0}f(x)=1=f(0)$ .

$x$ $y=f(x)$

$-0,01$ $0,99$

$-0,001$ $0,999$

$-0,0001$ $0,9999$

$\downarrow$ $\downarrow$

$0$ $1$

$\uparrow$ $\uparrow$

$0,0001$ $1,0001$

$0,001$ $1,001$

$0,01$ $1,01$

Código 1: Python

⬇

1from sympy.abc import x

2from sympy import limit

3limit((x**2-1)*(x-2)/((x-1)*(x-2)), x, 0)

⬇

1
•

$\displaystyle\lim_{x\to 1}f(x)=2$ , embora $f(1)$ não esteja definido.

$x$ $f(x)$

$0,9$ $1,9$

$0,99$ $1,99$

$0,999$ $1,999$

$\downarrow$ $\downarrow$

$1$ $2$

$\uparrow$ $\uparrow$

$1,0001$ $2,0001$

$1,001$ $2,001$

$1,01$ $2,01$

Código 2: Python

⬇

1from sympy.abc import x

2from sympy import limit

3limit((x**2-1)*(x-2)/((x-1)*(x-2)), x, 1)

⬇

2
•

$\displaystyle\lim_{x\to 2}f(x)=3$ , embora $f(2)$ também não esteja definido. Verifique!

$x$	$y=f(x)$
$-0,01$	$0,99$
$-0,001$	$0,999$
$-0,0001$	$0,9999$
$\downarrow$	$\downarrow$
$0$	$1$
$\uparrow$	$\uparrow$
$0,0001$	$1,0001$
$0,001$	$1,001$
$0,01$	$1,01$

$x$	$f(x)$
$0,9$	$1,9$
$0,99$	$1,99$
$0,999$	$1,999$
$\downarrow$	$\downarrow$
$1$	$2$
$\uparrow$	$\uparrow$
$1,0001$	$2,0001$
$1,001$	$2,001$
$1,01$	$2,01$

1.1.1 Limites da função constante e da função identidade

Da noção de limite, podemos inferir que

\lim_{x\to x_{0}}k=k,

(1.3)

seja qual for a constante $k$ . Consultemos a Figura 1.3.

Exemplo 1.1.2.

Vejamos os seguintes casos:

a)

$\displaystyle\lim_{x\to-1}1=1$

Código 3: Python

⬇

1from sympy.abc import x

2from sympy import limit

3limit(1, x, -1)

⬇

1
b)

$\displaystyle\lim_{x\to 2}-3=-3$
c)

$\displaystyle\lim_{x\to\pi}\left(\sqrt{2}-e\right)=\sqrt{2}-e$

Também da noção de limites, podemos inferir que

\lim_{x\to a}x=a,

(1.4)

seja qual for o ponto $a$ . Consultemos a Figura 1.4.

Código 4: Python

⬇

1from sympy.abc import x, a

2from sympy import limit

3limit(x, x, a)

⬇

Exemplo 1.1.3.

Estudemos os seguintes casos:

a)

$\displaystyle\lim_{x\to-1}x=-1$

Código 5: Python

⬇

1from sympy.abc import x

2from sympy import limit

3limit(x, x, -1)

⬇

-1
b)

$\displaystyle\lim_{x\to 2}x=2$
c)

$\displaystyle\lim_{x\to\pi}x=\pi$

1.1.2 Exercícios resolvidos

ER 1.1.1.

Estime o valor do limite

\lim_{x\to 1}e^{x}.

(1.5)

Solução.

Da noção de limite, podemos buscar inferir o limite de uma função em um ponto $x_{0}$ , computando seus valores próximos deste ponto. Por exemplo, construímos a seguinte tabela:

$x$	f(x)
$0,9$	$2,460$
$0,99$	$2,691$
$0,999$	$2,716$
$\downarrow$	$\downarrow$
$1$	$2,72$
$\uparrow$	$\uparrow$
$1,0001$	$2,719$
$1,001$	$2,721$
$1,01$	$2,746$

Com isso, inferimos que

\lim_{x\to 1}e^{x}\approx 2,72.

(1.6)

Mais adiante, veremos que $\lim_{x\to 1}e^{x}=e\approx 2,718281828459045...$ .

Código 6: Python

⬇

1from sympy.abc import x

2from sympy import limit, exp

3L = limit(exp(x), x, 1)

4print(f'{L} =', L.evalf())

⬇

E = 2.71828182845905

ER 1.1.2.

Considere que uma dada função $f$ tenha o seguinte esboço de gráfico:

Então, infira o valores de

a)

$\displaystyle\lim_{x\to-2}f(x)$
b)

$\displaystyle\lim_{x\to-1}f(x)$
c)

$\displaystyle\lim_{x\to 1}f(x)$

Solução.

a)

$\displaystyle\lim_{x\to-2}f(x)$

Para valores suficientemente próximos de $-2$ e a direita de $-2$ (i.e. $x>-2$ ), podemos observar que $f(x)=1$ . Para tais valores de $x$ a esquerda de $-2$ (i.e. $x<-2$ ), vemos que os valores de $f(x)$ tornam-se próximos de $1$ . Isto é, temos que os valores de $f(x)$ podemos ser tomados arbitrariamente próximos de $L=1$ , se tomarmos $x$ suficientemente próximo de $-2$ . Concluímos que

$\lim_{x\to-2}=1.$ (1.7)
b)

$\displaystyle\lim_{x\to-1}f(x)$

Mesmo sendo $f(-1)=2$ , observamos que os valores de $f(x)$ podem ser tomados arbitrariamente próximos de $1$ , se escolhemos valores de $x$ suficientemente próximos de $-1$ . Logo,

$\lim_{x\to-1}f(x)=1.$ (1.8)
c)

$\displaystyle\lim_{x\to 1}f(x)$

Aqui, para valores de $x$ suficientemente próximos de $x_{0}=1$ e a esquerda ( $x<1$ ), vemos que os valores de $f(x)$ são próximos de $L=2$ . Entretanto, para valores de $x$ suficientemente próximos de $x_{0}=1$ e a direita ( $x>1$ ), temos que os valores de $f(x)$ são próximos de $L=1$ . Ou seja, não é possível escolher um valor $L$ tal que $f(x)$ esteja arbitrariamente próxima ao tomarmos $x$ suficientemente próximo de $x_{0}=1$ , pois $L$ dependerá de $x$ estar a esquerda ou a direita de do ponto $x_{0}=1$ . Concluímos que este limite não existe, e escrevemos

$\not\exists\lim_{x\to 1}f(x).$ (1.9)

1.1.3 Exercícios

E. 1.1.1.

Considere que uma dada função $f$ tenha o seguinte esboço de gráfico:

Forneça o valor dos seguintes limites:

a)

$\displaystyle\lim_{x\to-1}f(x)$
b)

$\displaystyle\lim_{x\to 1}f(x)$
c)

$\displaystyle\lim_{x\to 2}f(x)$
d)

$\displaystyle\lim_{x\to 3}f(x)$

Resposta.

a) $-1$ ; b) $-1$ ; c) $2$ ; d) $\nexists$

E. 1.1.2.

Considerando a mesma função do exercício anterior (Exercício 1.1.1), forneça

1.

$\displaystyle\lim_{x\to-\frac{3}{2}}f(x)$
2.

$\displaystyle\lim_{x\to 0}f(x)$
3.

$\displaystyle\lim_{x\to\frac{3}{4}}f(x)$

Resposta.

a) $-\frac{3}{2}$ ; b) $-1$ ; c) $-1$

E. 1.1.3.

Forneça o valor dos seguintes limites:

a)

$\displaystyle\lim_{x\to 2}2$
b)

$\displaystyle\lim_{x\to-2}2$
c)

$\displaystyle\lim_{x\to 2}-3$
d)

$\displaystyle\lim_{x\to e}\pi$

Resposta.

a) 2; b) 2; c) -3; d) $\pi$

E. 1.1.4.

Forneça o valor dos seguintes limites:

a)

$\displaystyle\lim_{x\to 2}x$
b)

$\displaystyle\lim_{x\to-2}x$
c)

$\displaystyle\lim_{x\to-3}x$
d)

$\displaystyle\lim_{x\to e}x$

Resposta.

a) 2; b) -2; c) -3; d) $e$

E. 1.1.5.

Com base na noção de limites, calcule:

a)

$\displaystyle\lim_{x\to 1}|x|$
b)

$\displaystyle\lim_{x\to-1}|x|$
c)

$\displaystyle\lim_{x\to 10^{-10}}|x|$

Resposta.

a) $1$ ; b) $1$ ; c) $10^{-10}$

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Pedro H A Konzen

| | | |