Política de uso de dados

Ao navegar por este site, você concorda com a política de uso de dados.

Política de uso de dados

Ao navegar por este site, você concorda com a política de uso de dados.

| | | |

Cálculo I

1 Limites 1.2 Regras para o cálculo de limites 1.4 Limites no infinito

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

1.3 Limites laterais

Seja dada uma função $f$ definida para todo $x$ em um intervalo aberto $(a,x_{0})$ . O limite lateral à esquerda de $f$ no ponto $x_{0}$ é denotado por

\lim_{x\to{\color[rgb]{1,0,0}\definecolor[named]{pgfstrokecolor}{rgb}{1,0,0}% \pgfsys@color@rgb@stroke{1}{0}{0}\pgfsys@color@rgb@fill{1}{0}{0}x_{0}^{-}}}f(x)

(1.98)

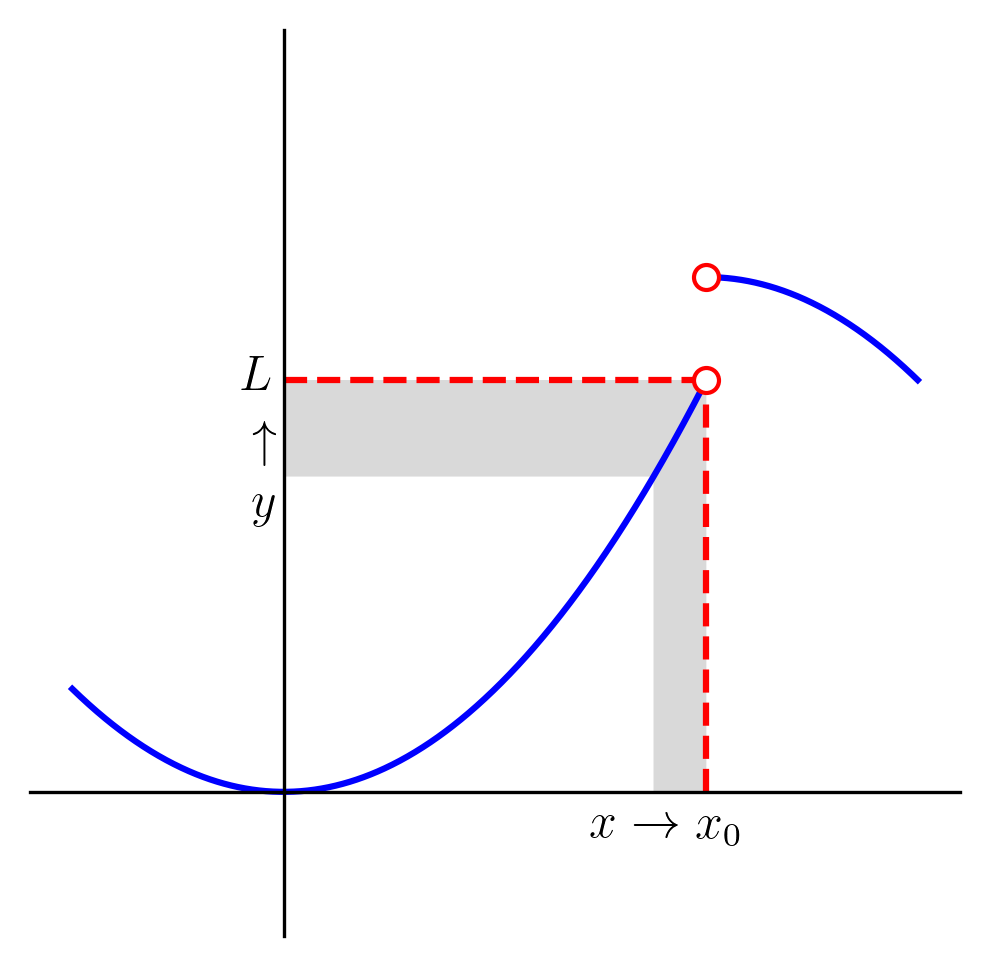
e é computado tendo em vista a tendência da função apenas para pontos $x<x_{0}$ . Em outras palavras, o

\lim_{x\to x_{0}^{-}}f(x)=L

(1.99)

quando $f(x)$ é arbitrariamente próximo de $L$ , para todo $x<x_{0}$ suficientemente próximo de $x_{0}$ . Veja a Figura 1.5.

Refer to caption — Figura 1.5: Limite lateral à esquerda.

Para uma função $f$ definida para todo $x$ em um intervalo aberto $(x_{0},b)$ , o limite lateral à direita de $f$ no ponto $x_{0}$ é denotado por

\lim_{x\to{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}x_{0}^{+}}}f(x)

(1.100)

e é computado tendo em vista a tendência da função apenas para pontos $x>x_{0}$ . Em outras palavras, temos

\lim_{x\to x_{0}^{+}}f(x)=L,

(1.101)

quando $f(x)$ é arbitrariamente próximo de $L$ , para todo $x>x_{0}$ suficientemente próximo de $x_{0}$ . Veja a Figura 1.6.

Observação 1.3.1.

Por inferência direta, temos

\lim_{x\to x_{0}^{\pm}}k=k

(1.102)

\lim_{x\to x_{0}^{\pm}}x=x_{0},

(1.103)

onde $x_{0}$ e $k$ são quaisquer dados números reais.

Exemplo 1.3.1.

Vamos calcular

\lim_{x\to 0^{-}}|x|.

(1.104)

Por definição, temos

|x|:=\left\{\begin{array}[]{ll}x&,x\geq 0,\\ -x&,x<0.\end{array}\right.

(1.105)

Como estamos interessados no limite lateral à esquerda de $x=0$ , trabalhamos com $x<0$ e, então

	$\displaystyle\lim_{x\to 0^{-}}\|x\|=\lim_{x\to 0^{-}}-x$		(1.106)
	$\displaystyle\text{}\quad=-\lim_{x\to 0^{-}}x=0.$		(1.107)

Analogamente, calculamos

\lim_{x\to 0^{+}}|x|=\lim_{x\to 0^{+}}x=0.

(1.108)

Verifique!

Com o Python+SymPy, podemos computar os limites acima com os seguintes comandos.

⬇

1 >>> from sympy import *

2 >>> x = Symbol("x")

3 >>> limit(abs(x), x, 0, '-')

4 0

5 >>> limit(abs(x), x, 0, '+')

6 0

Teorema 1.3.1.

Existe o limite de uma dada função $f$ no ponto $x=x_{0}$ e

\lim_{x\to x_{0}}f(x)=L

(1.109)

se, e somente se, existem e são iguais a $L$ os limites laterais à esquerda e à direita de $f$ no ponto $x=x_{0}$ .

Exemplo 1.3.2.

No exemplo anterior (Exemplo 1.3.1), vimos que

\lim_{x\to 0^{-}}|x|=\lim_{x\to 0^{+}}|x|=0.

(1.110)

Logo, pelo teorema acima (Teorema 1.3.1), podemos concluir que

\lim_{x\to 0}|x|=0.

(1.111)

Exemplo 1.3.3.

Vamos verificar a existência de

\lim_{x\to 0}\frac{|x|}{x}.

(1.112)

Começamos pelo limite lateral à esquerda, temos

	$\displaystyle\lim_{x\to 0^{-}}\frac{\|x\|}{x}=\lim_{x\to 0^{-}}\frac{-x}{x}$		(1.113)
	$\displaystyle\text{}\quad=\lim_{x\to 0^{-}}-1=-1.$		(1.114)

Agora, calculando o limite lateral à direta, obtemos

	$\displaystyle\lim_{x\to 0^{+}}\frac{\|x\|}{x}=\lim_{x\to 0^{+}}\frac{x}{x}$		(1.115)
	$\displaystyle\text{}\quad=\lim_{x\to 0^{+}}1=1.$		(1.116)

Como os limites laterais à esquerda e à direita são diferentes, concluímos que não existe o limite de $|x|/x$ no ponto $x=0$ .

Com o Python+SymPy, por padrão o limite computado é sempre o limite lateral à direita. É por isso que o comando

⬇

1 >>> from sympy import *

2 >>> x = Symbol("x")

3 >>> limit(abs(x)/x, x, 0)

4 1

fornece o valor $1$ como saída. Compute os limites laterais e verifique com os resultados analíticos obtidos acima!

Observação 1.3.2.

As regras básicas para o cálculo de limites bilaterais são estendidas para limites laterais. I.e., se

\lim_{x\to x_{0}^{\pm}}f(x)=L_{1}

(1.117)

\lim_{x\to x_{0}^{\pm}}g(x)=L_{2},

(1.118)

então valem a:

•

regra da multiplicação por um escalar:

$\lim_{x\to x_{0}^{\pm}}kf(x)=k\lim_{x\to x_{0}^{\pm}}f(x)=kL_{1},$ (1.119)

para qualquer número real $k$ .
•

regra da soma/subtração:

$\displaystyle\lim_{x\to x_{0}^{\pm}}f(x)\pm g(x)=\lim_{x\to x_{0}^{\pm}}f(x)% \pm\lim_{x\to x_{0}^{\pm}}g(x)$ (1.120)

$\displaystyle\text{}\quad=L_{1}+L_{2}$ (1.121)
•

regra do produto:

$\displaystyle\lim_{x\to x_{0}^{\pm}}f(x)\cdot g(x)=\lim_{x\to x_{0}^{\pm}}f(x)% \cdot\lim_{x\to x_{0}^{\pm}}g(x)$ (1.122)

$\displaystyle\text{}\quad=L_{1}\cdot L_{2}$ (1.123)
•

regra do quociente:

$\displaystyle\lim_{x\to x_{0}^{\pm}}\frac{f(x)}{g(x)}=\frac{\lim_{x\to x_{0}^{% \pm}}f(x)}{\lim_{x\to x_{0}^{\pm}}g(x)}$ (1.124)

$\displaystyle\text{}\quad=\frac{L_{1}}{L_{2}},$ (1.125)

desde que $L_{2}\neq 0$ .
•

regra da potenciação:

$\displaystyle\lim_{x\to x_{0}^{\pm}}(f(x))^{s}=\left(\lim_{x\to x_{0}^{\pm}}f(% x)\right)^{s}$ (1.126)

$\displaystyle\text{}\quad=L_{1}^{s},$ (1.127)

se, adicionalmente, $L_{1}^{s}$ é um número real.

1.3.1 Exercícios resolvidos

ER 1.3.1.

Considere que uma dada função $f$ tenha o seguinte esboço de gráfico:

Então, infira o valores de

a)

$\displaystyle\lim_{x\to-2^{-}}f(x)$
b)

$\displaystyle\lim_{x\to-1^{+}}f(x)$
c)

$\displaystyle\lim_{x\to 1^{-}}f(x)$
d)

$\displaystyle\lim_{x\to 1^{+}}f(x)$
e)

$\displaystyle\lim_{x\to 1}f(x)$

Solução.

a)

$\displaystyle\lim_{x\to-2^{-}}f(x)$

Para valores $x<-2$ e suficientemente próximos de $-2$ , podemos observar que $f(x)$ fica arbitrariamente próximo de $1$ . Concluímos que

$\lim_{x\to-2^{-}}=1.$ (1.128)
b)

$\displaystyle\lim_{x\to-1^{+}}f(x)$

Mesmo sendo $f(-1)=2$ , observamos que os valores de $f(x)$ podem ser tomados arbitrariamente próximos de $1$ , se escolhemos valores de $x>-1$ e suficientemente próximos de $-1$ . Logo,

$\lim_{x\to-1^{+}}f(x)=1.$ (1.129)
c)

$\displaystyle\lim_{x\to 1^{-}}f(x)$

Observamos que os valores de $f(x)$ podem ser tomados arbitrariamente próximos de $2$ , se escolhemos valores de $x<1$ e suficientemente próximos de $1$ . Logo,

$\lim_{x\to 1^{-}}f(x)=2.$ (1.130)

Notamos também que, neste caso, $f(x)$ não tende para $f(1)=1$ quando $x$ tende a $1$ pela esquerda.
d)

$\displaystyle\lim_{x\to 1^{+}}f(x)$

Observamos que os valores de $f(x)$ podem ser tomados arbitrariamente próximos de $1$ , se escolhemos valores de $x>1$ e suficientemente próximos de $1$ . Logo,

$\lim_{x\to 1^{+}}f(x)=1.$ (1.131)

Aqui, $f(x)\to f(1)=1$ quando $x\to 1^{+}$ .
e)

$\displaystyle\lim_{x\to 1}f(x)$

Nos itens anteriores, vimos que

$2=\lim_{x\to 1^{-}}f(x)\neq\lim_{x\to 1^{+}}f(x)=1.$ (1.132)

Logo, concluímos que este limite não existe, e escrevemos

$\not\exists\lim_{x\to 1}f(x).$ (1.133)

ER 1.3.2.

Calcule $\lim_{x\to-1}f(x)$ para

f(x)=\left\{\begin{array}[]{ll}(x+1)^{2}-1&,x<-1,\\ x&,x>-1.\end{array}\right.

(1.134)

Solução.

A função $f$ tem comportamentos distintos para valores à esquerda e à direita de $x_{0}=-1$ . Portanto, para calcularmos $\lim_{x\to-1}f(x)$ precisamos calcular os limites laterais. Temos:

	$\displaystyle\lim_{x\to-1^{-}}f(x)=\lim_{x\to-1^{-}}(x+1)^{2}-1$		(1.135)
	$\displaystyle\text{}\quad=(-1+1)^{2}-1=-1,$		(1.136)

	$\displaystyle\lim_{x\to-1^{+}}f(x)=\lim_{x\to-1^{+}}x$		(1.137)
	$\displaystyle\text{}\quad=-1.$		(1.138)

Como ambos os limites laterais são iguais a $-1$ , concluímos que

\lim_{x\to-1}f(x)=-1.

(1.139)

1.3.2 Exercícios

E. 1.3.1.

Considere que uma dada função $f$ tenha o seguinte esboço de gráfico:

Forneça o valor dos seguintes limites:

a)

$\displaystyle\lim_{x\to 2^{+}}f(x)$
b)

$\displaystyle\lim_{x\to 2^{-}}f(x)$
c)

$\displaystyle\lim_{x\to 2}f(x)$
d)

$\displaystyle\lim_{x\to 3^{+}}f(x)$
e)

$\displaystyle\lim_{x\to 3^{-}}f(x)$
f)

$\displaystyle\lim_{x\to 3}f(x)$

Resposta.

a) $2$ ; b) $2$ ; c) $2$ ; d) $2$ ; e) $1$ ; f) $\nexists$

E. 1.3.2.

Sendo

f(x)=\left\{\begin{array}[]{ll}x^{2}+1&,x\leq 1,\\ 2x&,x>1.\end{array}\right.

(1.140)

calcule

a)

$\displaystyle\lim_{x\to 1^{-}}f(x)$ .
b)

$\displaystyle\lim_{x\to 1^{+}}f(x)$ .
c)

$\displaystyle\lim_{x\to 1}f(x)$ .

Resposta.

a) $2$ ; b) $2$ ; c) $2$

E. 1.3.3.

Sendo

f(x)=\left\{\begin{array}[]{ll}x^{2}+1&,x\leq 1,\\ 2x+1&,x>1,\end{array}\right.

(1.141)

calcule

a)

$\displaystyle\lim_{x\to 1^{-}}f(x)$ .
b)

$\displaystyle\lim_{x\to 1^{+}}f(x)$ .
c)

$\displaystyle\lim_{x\to 1}f(x)$ .

Resposta.

a) $2$ ; b) $3$ ; c) $\nexists$

E. 1.3.4.

Calcule

\lim_{x\to 0^{-}}\frac{x}{2|x|}.

(1.142)

Resposta.

$-\frac{1}{2}$

E. 1.3.5.

Calcule

\lim_{x\to-1^{+}}\sqrt{1-x^{2}}.

(1.143)

O que pode-se dizer sobre o limite à esquerda?

Resposta.

$0$ ; Não está definido, pois o domínio de $f(x)=\sqrt{1-x^{2}}$ é $[-1,1]$ .

E. 1.3.6.

Diga se é verdadeira ou falsa a seguinte afirmação. Se existem

	$\displaystyle\lim_{x\to 1^{-}}f(x)=L$		(1.144)
	$\displaystyle\lim_{x\to 1^{+}}g(x)=M$		(1.145)

então

\lim_{x\to 1^{-}}f(x)+g(x)=L+M.

(1.146)

Justifique sua resposta.

Resposta.

Falso. Dica: construa um contraexemplo para mostrar que a afirmação não é verdadeira.

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Cálculo I

1 Limites 1.2 Regras para o cálculo de limites 1.4 Limites no infinito

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

1.3 Limites laterais

Seja dada uma função $f$ definida para todo $x$ em um intervalo aberto $(a,x_{0})$ . O limite lateral à esquerda de $f$ no ponto $x_{0}$ é denotado por

\lim_{x\to{\color[rgb]{1,0,0}\definecolor[named]{pgfstrokecolor}{rgb}{1,0,0}% \pgfsys@color@rgb@stroke{1}{0}{0}\pgfsys@color@rgb@fill{1}{0}{0}x_{0}^{-}}}f(x)

(1.98)

e é computado tendo em vista a tendência da função apenas para pontos $x<x_{0}$ . Em outras palavras, o

\lim_{x\to x_{0}^{-}}f(x)=L

(1.99)

quando $f(x)$ é arbitrariamente próximo de $L$ , para todo $x<x_{0}$ suficientemente próximo de $x_{0}$ . Veja a Figura 1.5.

Para uma função $f$ definida para todo $x$ em um intervalo aberto $(x_{0},b)$ , o limite lateral à direita de $f$ no ponto $x_{0}$ é denotado por

\lim_{x\to{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}x_{0}^{+}}}f(x)

(1.100)

e é computado tendo em vista a tendência da função apenas para pontos $x>x_{0}$ . Em outras palavras, temos

\lim_{x\to x_{0}^{+}}f(x)=L,

(1.101)

quando $f(x)$ é arbitrariamente próximo de $L$ , para todo $x>x_{0}$ suficientemente próximo de $x_{0}$ . Veja a Figura 1.6.

Observação 1.3.1.

Por inferência direta, temos

\lim_{x\to x_{0}^{\pm}}k=k

(1.102)

\lim_{x\to x_{0}^{\pm}}x=x_{0},

(1.103)

onde $x_{0}$ e $k$ são quaisquer dados números reais.

Exemplo 1.3.1.

Vamos calcular

\lim_{x\to 0^{-}}|x|.

(1.104)

Por definição, temos

|x|:=\left\{\begin{array}[]{ll}x&,x\geq 0,\\ -x&,x<0.\end{array}\right.

(1.105)

Como estamos interessados no limite lateral à esquerda de $x=0$ , trabalhamos com $x<0$ e, então

	$\displaystyle\lim_{x\to 0^{-}}\|x\|=\lim_{x\to 0^{-}}-x$		(1.106)
	$\displaystyle\text{}\quad=-\lim_{x\to 0^{-}}x=0.$		(1.107)

Analogamente, calculamos

\lim_{x\to 0^{+}}|x|=\lim_{x\to 0^{+}}x=0.

(1.108)

Verifique!

Com o Python+SymPy, podemos computar os limites acima com os seguintes comandos.

⬇

1 >>> from sympy import *

2 >>> x = Symbol("x")

3 >>> limit(abs(x), x, 0, '-')

4 0

5 >>> limit(abs(x), x, 0, '+')

6 0

Teorema 1.3.1.

Existe o limite de uma dada função $f$ no ponto $x=x_{0}$ e

\lim_{x\to x_{0}}f(x)=L

(1.109)

se, e somente se, existem e são iguais a $L$ os limites laterais à esquerda e à direita de $f$ no ponto $x=x_{0}$ .

Exemplo 1.3.2.

No exemplo anterior (Exemplo 1.3.1), vimos que

\lim_{x\to 0^{-}}|x|=\lim_{x\to 0^{+}}|x|=0.

(1.110)

Logo, pelo teorema acima (Teorema 1.3.1), podemos concluir que

\lim_{x\to 0}|x|=0.

(1.111)

Exemplo 1.3.3.

Vamos verificar a existência de

\lim_{x\to 0}\frac{|x|}{x}.

(1.112)

Começamos pelo limite lateral à esquerda, temos

	$\displaystyle\lim_{x\to 0^{-}}\frac{\|x\|}{x}=\lim_{x\to 0^{-}}\frac{-x}{x}$		(1.113)
	$\displaystyle\text{}\quad=\lim_{x\to 0^{-}}-1=-1.$		(1.114)

Agora, calculando o limite lateral à direta, obtemos

	$\displaystyle\lim_{x\to 0^{+}}\frac{\|x\|}{x}=\lim_{x\to 0^{+}}\frac{x}{x}$		(1.115)
	$\displaystyle\text{}\quad=\lim_{x\to 0^{+}}1=1.$		(1.116)

Como os limites laterais à esquerda e à direita são diferentes, concluímos que não existe o limite de $|x|/x$ no ponto $x=0$ .

Com o Python+SymPy, por padrão o limite computado é sempre o limite lateral à direita. É por isso que o comando

⬇

1 >>> from sympy import *

2 >>> x = Symbol("x")

3 >>> limit(abs(x)/x, x, 0)

4 1

fornece o valor $1$ como saída. Compute os limites laterais e verifique com os resultados analíticos obtidos acima!

Observação 1.3.2.

As regras básicas para o cálculo de limites bilaterais são estendidas para limites laterais. I.e., se

\lim_{x\to x_{0}^{\pm}}f(x)=L_{1}

(1.117)

\lim_{x\to x_{0}^{\pm}}g(x)=L_{2},

(1.118)

então valem a:

•

regra da multiplicação por um escalar:

$\lim_{x\to x_{0}^{\pm}}kf(x)=k\lim_{x\to x_{0}^{\pm}}f(x)=kL_{1},$ (1.119)

para qualquer número real $k$ .
•

regra da soma/subtração:

$\displaystyle\lim_{x\to x_{0}^{\pm}}f(x)\pm g(x)=\lim_{x\to x_{0}^{\pm}}f(x)% \pm\lim_{x\to x_{0}^{\pm}}g(x)$ (1.120)

$\displaystyle\text{}\quad=L_{1}+L_{2}$ (1.121)
•

regra do produto:

$\displaystyle\lim_{x\to x_{0}^{\pm}}f(x)\cdot g(x)=\lim_{x\to x_{0}^{\pm}}f(x)% \cdot\lim_{x\to x_{0}^{\pm}}g(x)$ (1.122)

$\displaystyle\text{}\quad=L_{1}\cdot L_{2}$ (1.123)
•

regra do quociente:

$\displaystyle\lim_{x\to x_{0}^{\pm}}\frac{f(x)}{g(x)}=\frac{\lim_{x\to x_{0}^{% \pm}}f(x)}{\lim_{x\to x_{0}^{\pm}}g(x)}$ (1.124)

$\displaystyle\text{}\quad=\frac{L_{1}}{L_{2}},$ (1.125)

desde que $L_{2}\neq 0$ .
•

regra da potenciação:

$\displaystyle\lim_{x\to x_{0}^{\pm}}(f(x))^{s}=\left(\lim_{x\to x_{0}^{\pm}}f(% x)\right)^{s}$ (1.126)

$\displaystyle\text{}\quad=L_{1}^{s},$ (1.127)

se, adicionalmente, $L_{1}^{s}$ é um número real.

1.3.1 Exercícios resolvidos

ER 1.3.1.

Considere que uma dada função $f$ tenha o seguinte esboço de gráfico:

Então, infira o valores de

a)

$\displaystyle\lim_{x\to-2^{-}}f(x)$
b)

$\displaystyle\lim_{x\to-1^{+}}f(x)$
c)

$\displaystyle\lim_{x\to 1^{-}}f(x)$
d)

$\displaystyle\lim_{x\to 1^{+}}f(x)$
e)

$\displaystyle\lim_{x\to 1}f(x)$

Solução.

a)

$\displaystyle\lim_{x\to-2^{-}}f(x)$

Para valores $x<-2$ e suficientemente próximos de $-2$ , podemos observar que $f(x)$ fica arbitrariamente próximo de $1$ . Concluímos que

$\lim_{x\to-2^{-}}=1.$ (1.128)
b)

$\displaystyle\lim_{x\to-1^{+}}f(x)$

Mesmo sendo $f(-1)=2$ , observamos que os valores de $f(x)$ podem ser tomados arbitrariamente próximos de $1$ , se escolhemos valores de $x>-1$ e suficientemente próximos de $-1$ . Logo,

$\lim_{x\to-1^{+}}f(x)=1.$ (1.129)
c)

$\displaystyle\lim_{x\to 1^{-}}f(x)$

Observamos que os valores de $f(x)$ podem ser tomados arbitrariamente próximos de $2$ , se escolhemos valores de $x<1$ e suficientemente próximos de $1$ . Logo,

$\lim_{x\to 1^{-}}f(x)=2.$ (1.130)

Notamos também que, neste caso, $f(x)$ não tende para $f(1)=1$ quando $x$ tende a $1$ pela esquerda.
d)

$\displaystyle\lim_{x\to 1^{+}}f(x)$

Observamos que os valores de $f(x)$ podem ser tomados arbitrariamente próximos de $1$ , se escolhemos valores de $x>1$ e suficientemente próximos de $1$ . Logo,

$\lim_{x\to 1^{+}}f(x)=1.$ (1.131)

Aqui, $f(x)\to f(1)=1$ quando $x\to 1^{+}$ .
e)

$\displaystyle\lim_{x\to 1}f(x)$

Nos itens anteriores, vimos que

$2=\lim_{x\to 1^{-}}f(x)\neq\lim_{x\to 1^{+}}f(x)=1.$ (1.132)

Logo, concluímos que este limite não existe, e escrevemos

$\not\exists\lim_{x\to 1}f(x).$ (1.133)

ER 1.3.2.

Calcule $\lim_{x\to-1}f(x)$ para

f(x)=\left\{\begin{array}[]{ll}(x+1)^{2}-1&,x<-1,\\ x&,x>-1.\end{array}\right.

(1.134)

Solução.

A função $f$ tem comportamentos distintos para valores à esquerda e à direita de $x_{0}=-1$ . Portanto, para calcularmos $\lim_{x\to-1}f(x)$ precisamos calcular os limites laterais. Temos:

	$\displaystyle\lim_{x\to-1^{-}}f(x)=\lim_{x\to-1^{-}}(x+1)^{2}-1$		(1.135)
	$\displaystyle\text{}\quad=(-1+1)^{2}-1=-1,$		(1.136)

	$\displaystyle\lim_{x\to-1^{+}}f(x)=\lim_{x\to-1^{+}}x$		(1.137)
	$\displaystyle\text{}\quad=-1.$		(1.138)

Como ambos os limites laterais são iguais a $-1$ , concluímos que

\lim_{x\to-1}f(x)=-1.

(1.139)

1.3.2 Exercícios

E. 1.3.1.

Considere que uma dada função $f$ tenha o seguinte esboço de gráfico:

Forneça o valor dos seguintes limites:

a)

$\displaystyle\lim_{x\to 2^{+}}f(x)$
b)

$\displaystyle\lim_{x\to 2^{-}}f(x)$
c)

$\displaystyle\lim_{x\to 2}f(x)$
d)

$\displaystyle\lim_{x\to 3^{+}}f(x)$
e)

$\displaystyle\lim_{x\to 3^{-}}f(x)$
f)

$\displaystyle\lim_{x\to 3}f(x)$

Resposta.

a) $2$ ; b) $2$ ; c) $2$ ; d) $2$ ; e) $1$ ; f) $\nexists$

E. 1.3.2.

Sendo

f(x)=\left\{\begin{array}[]{ll}x^{2}+1&,x\leq 1,\\ 2x&,x>1.\end{array}\right.

(1.140)

calcule

a)

$\displaystyle\lim_{x\to 1^{-}}f(x)$ .
b)

$\displaystyle\lim_{x\to 1^{+}}f(x)$ .
c)

$\displaystyle\lim_{x\to 1}f(x)$ .

Resposta.

a) $2$ ; b) $2$ ; c) $2$

E. 1.3.3.

Sendo

f(x)=\left\{\begin{array}[]{ll}x^{2}+1&,x\leq 1,\\ 2x+1&,x>1,\end{array}\right.

(1.141)

calcule

a)

$\displaystyle\lim_{x\to 1^{-}}f(x)$ .
b)

$\displaystyle\lim_{x\to 1^{+}}f(x)$ .
c)

$\displaystyle\lim_{x\to 1}f(x)$ .

Resposta.

a) $2$ ; b) $3$ ; c) $\nexists$

E. 1.3.4.

Calcule

\lim_{x\to 0^{-}}\frac{x}{2|x|}.

(1.142)

Resposta.

$-\frac{1}{2}$

E. 1.3.5.

Calcule

\lim_{x\to-1^{+}}\sqrt{1-x^{2}}.

(1.143)

O que pode-se dizer sobre o limite à esquerda?

Resposta.

$0$ ; Não está definido, pois o domínio de $f(x)=\sqrt{1-x^{2}}$ é $[-1,1]$ .

E. 1.3.6.

Diga se é verdadeira ou falsa a seguinte afirmação. Se existem

	$\displaystyle\lim_{x\to 1^{-}}f(x)=L$		(1.144)
	$\displaystyle\lim_{x\to 1^{+}}g(x)=M$		(1.145)

então

\lim_{x\to 1^{-}}f(x)+g(x)=L+M.

(1.146)

Justifique sua resposta.

Resposta.

Falso. Dica: construa um contraexemplo para mostrar que a afirmação não é verdadeira.

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Pedro H A Konzen

| | | |

	$\displaystyle\lim_{x\to x_{0}^{\pm}}f(x)\pm g(x)=\lim_{x\to x_{0}^{\pm}}f(x)% \pm\lim_{x\to x_{0}^{\pm}}g(x)$		(1.120)
	$\displaystyle\text{}\quad=L_{1}+L_{2}$		(1.121)

	$\displaystyle\lim_{x\to x_{0}^{\pm}}f(x)\cdot g(x)=\lim_{x\to x_{0}^{\pm}}f(x)% \cdot\lim_{x\to x_{0}^{\pm}}g(x)$		(1.122)
	$\displaystyle\text{}\quad=L_{1}\cdot L_{2}$		(1.123)

	$\displaystyle\lim_{x\to x_{0}^{\pm}}\frac{f(x)}{g(x)}=\frac{\lim_{x\to x_{0}^{% \pm}}f(x)}{\lim_{x\to x_{0}^{\pm}}g(x)}$		(1.124)
	$\displaystyle\text{}\quad=\frac{L_{1}}{L_{2}},$		(1.125)

	$\displaystyle\lim_{x\to x_{0}^{\pm}}(f(x))^{s}=\left(\lim_{x\to x_{0}^{\pm}}f(% x)\right)^{s}$		(1.126)
	$\displaystyle\text{}\quad=L_{1}^{s},$		(1.127)