Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Cálculo I
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
5.1 Cálculo de áreas
A integral definida está associada a área entre o gráfico da função e o eixo das abscissas no intervalo (consulte Figura 5.1). Ocorre que se for não negativa, então . Se for negativa, então . Por isso, dizemos que é a área líquida (ou com sinal) entre o gráfico de e o eixo das abscissas.
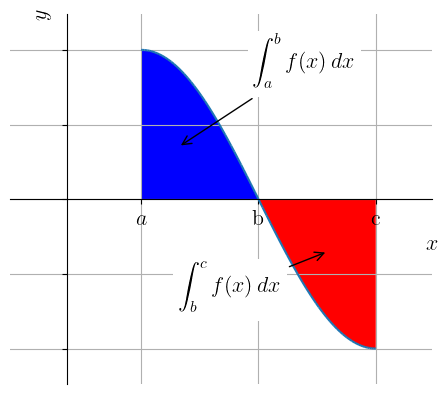
Exemplo 5.1.1.
Vamos calcular a área total entre o gráfico de e o eixo das abscissas, restrito ao intervalo .
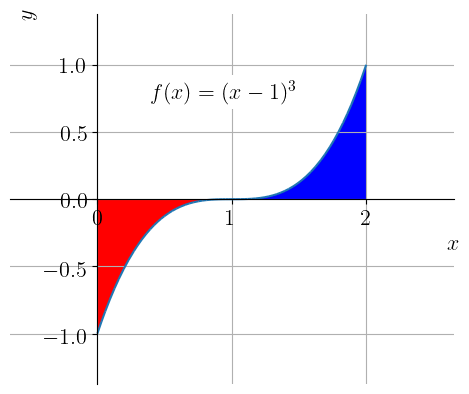
Começamos fazendo o estudo de sinal de no intervalo. Como para e, para , temos que em e em . Logo, a área total é dada por
| (5.1) |
Agora, usando a substituição , temos e segue que
| (5.2) | ||||
| (5.3) | ||||
| (5.4) | ||||
| (5.5) |
Então, do Teorema Fundamental do Cálculo, obtemos
| (5.6) | ||||
| (5.7) | ||||
| (5.8) | ||||
| (5.9) |
5.1.1 Áreas entre curvas
Observamos que se no intervalo , então
| (5.10) |
corresponde à área entre as curvas e restritas ao intervalo . Ou seja, fazendo , temos que
| (5.11) |
é a área entre essas curvas restritas ao intervalo . Ainda, se , entre a área entre elas é dada por
| (5.12) |
Exemplo 5.1.2.
Vamos calcular a área entre as curvas , , e .
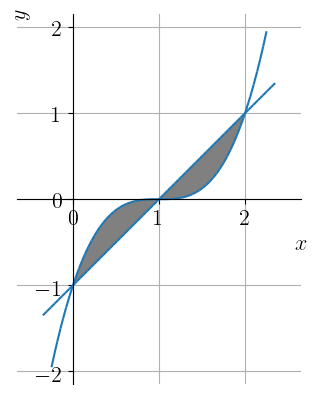
Começamos definindo . A fim de fazermos o estudo de sinal de , identificamos seus zeros.
| (5.13) | ||||
| (5.14) | ||||
| (5.15) | ||||
| (5.16) |
Ou seja, , e são as raízes de . Daí, segue seu estudo de sinal:
| - | + | |
| + | + | |
| - | - | |
| + | - |
Assim, temos que a área desejada pode ser calculada como
| (5.17) |
Agora, calculamos a integral de , i.e.
| (5.18) | ||||
| (5.19) | ||||
| (5.20) |
Por fim, do Teorema Fundamental do Cálculo, obtemos
| (5.21) | ||||
| (5.22) | ||||
| (5.23) | ||||
| (5.24) |
Calculando áreas em função de
Exemplo 5.1.3.
Calcule a área determinada pelas curvas e .
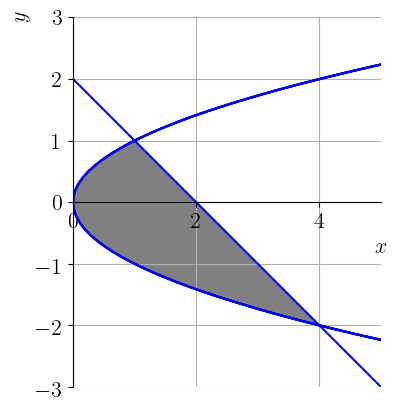
Uma das formas mais práticas de calcular esta área é integrando em relação a . Para isso, precisamos que as curvas sejam descritas por funções de em . A parábola já está escrita como tal, e a reta é equivalente a . Com isso, temos que a área determinada por estas curvas tem medida
| (5.25) | ||||
| (5.26) | ||||
| (5.27) | ||||
| (5.28) |
5.1.2 Exercícios resolvidos
ER 5.1.1.
Cálculo a área entre a reta e o gráfico de restritas ao intervalo .
Solução 0.
Observamos que a medida desta área corresponde à área do quadrado descontada a área sob o gráfico de restrita ao intervalo . Isto é,
| (5.29) | ||||
| (5.30) | ||||
| (5.31) |
ER 5.1.2.
Calcule a área entre as curvas , , e .
Solução 0.
O problema é equivalente a calcular a área entre os gráficos das funções e restritas ao intervalo . Como neste intervalo, temos
| (5.32) | ||||
| (5.33) | ||||
| (5.34) | ||||
| (5.35) |
ER 5.1.3.
Calcule a área entre o gráfico de e o eixo das abscissas no intervalo .
Solução 0.
Para calcularmos a área entre o gráfico de e o eixo das abscissas no intervalo , fazemos:
-
1.
O estudo de sinal de no intervalo .
-
(a)
Cálculo das raízes de no intervalo .
(5.36) (5.37) (5.38) -
(b)
Os sinais de .
(5.39) (5.40)
-
(a)
-
2.
Cálculo da área usando integrais definidas.
-
(a)
Cálculo da integral indefinida.
(5.41) (5.42) (5.43) -
(b)
Cálculo da área.
(5.44) (5.45) (5.46)
-
(a)
Com Python+SymPy, podemos fazer o estudo de sinal de com os seguintes comandos
E, então, computamos a área com
5.1.3 Exercícios
E. 5.1.1.
Calcule a área entre o gráfico de e o eixo das abscissas, restrita ao intervalo .
Resposta 0.
E. 5.1.2.
Calcule a área entre o gráfico de e o eixo das abscissas, restrita ao intervalo .
Resposta 0.
E. 5.1.3.
Calcule a área entre o gráfico de e a reta restritas ao intervalo .
Resposta 0.
E. 5.1.4.
Calcule a área entre as curvas , , e .
Resposta 0.
E. 5.1.5.
Calcule a área determinada pelas curvas e .
Resposta 0.
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.
Cálculo I
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
5.1 Cálculo de áreas
A integral definida está associada a área entre o gráfico da função e o eixo das abscissas no intervalo (consulte Figura 5.1). Ocorre que se for não negativa, então . Se for negativa, então . Por isso, dizemos que é a área líquida (ou com sinal) entre o gráfico de e o eixo das abscissas.

Exemplo 5.1.1.
Vamos calcular a área total entre o gráfico de e o eixo das abscissas, restrito ao intervalo .

Começamos fazendo o estudo de sinal de no intervalo. Como para e, para , temos que em e em . Logo, a área total é dada por
| (5.1) |
Agora, usando a substituição , temos e segue que
| (5.2) | ||||
| (5.3) | ||||
| (5.4) | ||||
| (5.5) |
Então, do Teorema Fundamental do Cálculo, obtemos
| (5.6) | ||||
| (5.7) | ||||
| (5.8) | ||||
| (5.9) |
5.1.1 Áreas entre curvas
Observamos que se no intervalo , então
| (5.10) |
corresponde à área entre as curvas e restritas ao intervalo . Ou seja, fazendo , temos que
| (5.11) |
é a área entre essas curvas restritas ao intervalo . Ainda, se , entre a área entre elas é dada por
| (5.12) |
Exemplo 5.1.2.
Vamos calcular a área entre as curvas , , e .

Começamos definindo . A fim de fazermos o estudo de sinal de , identificamos seus zeros.
| (5.13) | ||||
| (5.14) | ||||
| (5.15) | ||||
| (5.16) |
Ou seja, , e são as raízes de . Daí, segue seu estudo de sinal:
| - | + | |
| + | + | |
| - | - | |
| + | - |
Assim, temos que a área desejada pode ser calculada como
| (5.17) |
Agora, calculamos a integral de , i.e.
| (5.18) | ||||
| (5.19) | ||||
| (5.20) |
Por fim, do Teorema Fundamental do Cálculo, obtemos
| (5.21) | ||||
| (5.22) | ||||
| (5.23) | ||||
| (5.24) |
Calculando áreas em função de
Exemplo 5.1.3.
Calcule a área determinada pelas curvas e .

Uma das formas mais práticas de calcular esta área é integrando em relação a . Para isso, precisamos que as curvas sejam descritas por funções de em . A parábola já está escrita como tal, e a reta é equivalente a . Com isso, temos que a área determinada por estas curvas tem medida
| (5.25) | ||||
| (5.26) | ||||
| (5.27) | ||||
| (5.28) |
5.1.2 Exercícios resolvidos
ER 5.1.1.
Cálculo a área entre a reta e o gráfico de restritas ao intervalo .
Solução 0.
Observamos que a medida desta área corresponde à área do quadrado descontada a área sob o gráfico de restrita ao intervalo . Isto é,
| (5.29) | ||||
| (5.30) | ||||
| (5.31) |
ER 5.1.2.
Calcule a área entre as curvas , , e .
Solução 0.
O problema é equivalente a calcular a área entre os gráficos das funções e restritas ao intervalo . Como neste intervalo, temos
| (5.32) | ||||
| (5.33) | ||||
| (5.34) | ||||
| (5.35) |
ER 5.1.3.
Calcule a área entre o gráfico de e o eixo das abscissas no intervalo .
Solução 0.
Para calcularmos a área entre o gráfico de e o eixo das abscissas no intervalo , fazemos:
-
1.
O estudo de sinal de no intervalo .
-
(a)
Cálculo das raízes de no intervalo .
(5.36) (5.37) (5.38) -
(b)
Os sinais de .
(5.39) (5.40)
-
(a)
-
2.
Cálculo da área usando integrais definidas.
-
(a)
Cálculo da integral indefinida.
(5.41) (5.42) (5.43) -
(b)
Cálculo da área.
(5.44) (5.45) (5.46)
-
(a)
Com Python+SymPy, podemos fazer o estudo de sinal de com os seguintes comandos
E, então, computamos a área com
5.1.3 Exercícios
E. 5.1.1.
Calcule a área entre o gráfico de e o eixo das abscissas, restrita ao intervalo .
Resposta 0.
E. 5.1.2.
Calcule a área entre o gráfico de e o eixo das abscissas, restrita ao intervalo .
Resposta 0.
E. 5.1.3.
Calcule a área entre o gráfico de e a reta restritas ao intervalo .
Resposta 0.
E. 5.1.4.
Calcule a área entre as curvas , , e .
Resposta 0.
E. 5.1.5.
Calcule a área determinada pelas curvas e .
Resposta 0.
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.