Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Algoritmos e Programação I
2.2 Algoritmos e programação
Programar é criar um programa (um software) para ser executado em computador. Para isso, escreve-se um código em uma linguagem computacional (por exemplo, em Python), o qual é interpretado/compilado para gerar o programa final. Linguagens computacionais são técnicas, utilizam uma sintaxe simples, precisa e sem ambiguidades. Ou seja, para criarmos um programa com um determinado objetivo, precisamos escrever um código computacional técnico, que siga a sintaxe da linguagem escolhida e sem ambiguidades.
Um algoritmo pode ser definido uma sequencia ordenada e sem ambiguidade de passos para a resolução de um problema.
Exemplo 2.2.1.
O cálculo da área de um triângulo de base e altura dadas por ser feito com o seguinte algoritmo:
-
1.
Informe o valor da base .
-
2.
Informe o valor da altura .
-
3.
.
-
4.
Imprima o valor de .
Algoritmos para a programação são pensados para serem facilmente transformados em códigos computacionais. Por exemplo, o algoritmo acima pode ser escrito em Python como segue:
Para criar um programa para resolver um dado problema, começamos desenvolvendo um algoritmo para resolvê-lo, este algoritmo é implementado na linguagem computacional escolhida, a qual gera o programa final. Aqui, o passo mais difícil costuma ser o desenvolvimento do algoritmo. Precisamos pensar em como podemos resolver o problema de interesse em uma sequência de passos ordenada e sem ambiguidades para que possamos implementá-los em computador.
Um algoritmo deve ter as seguintes propriedades:
-
•
Cada passo deve estar bem definido, i.e. não pode conter ambiguidades.
-
•
Cada passo deve contribuir de forma efetiva na solução do problema.
-
•
Deve ter número finito de passos que podem ser computados em um tempo finito.
Observação 2.2.1.(Mulher na matemática)
A primeira pessoa a publicar um algoritmo para programação foi Augusta Ada King77endnote: 7Augusta Ada Byron King, Condessa de Lovelace, 1815 - 1852, matemática inglesa. Fonte: Wikipédia: Ada Lovelace.. O algoritmo foi criado para computar os números de Bernoulli88endnote: 8Jacob Bernoulli, 1655-1705, matemático suíço. Fonte: Wikipédia: Jakob Bernoulli..
2.2.1 Fluxograma
Fluxograma é uma representação gráfica de um algoritmo. Entre outras, usam-se as seguintes formas para representar tipos de ações a serem executadas:
-
•
Terminal: início ou final do algoritmo.
![[Uncaptioned image]](cap_lingua/dados/fig_fluxograma/terminal.png)
-
•
Linha de fluxo: direciona para a próxima execução.
![[Uncaptioned image]](cap_lingua/dados/fig_fluxograma/linha.png)
-
•
Entrada: leitura de informação/dados.
![[Uncaptioned image]](cap_lingua/dados/fig_fluxograma/entrada.png)
-
•
Processo: ação a ser executada.
![[Uncaptioned image]](cap_lingua/dados/fig_fluxograma/processo.png)
-
•
Decisão: ramificação do processamento baseada em uma condição.
![[Uncaptioned image]](cap_lingua/dados/fig_fluxograma/decisao.png)
-
•
Saída: impressão de informação/dados.
![[Uncaptioned image]](cap_lingua/dados/fig_fluxograma/saida.png)
Exemplo 2.2.2.
O método de Heron99endnote: 9Heron de Alexandria, 10 - 80, matemático grego. Fonte: Wikipédia: Heron de Alexandria. é um algoritmo para o cálculo aproximado da raiz quadrada de um dado número , i.e. . Consiste na iteração
| (2.1) | |||
| (2.2) |
para , onde é o número de iterações calculadas.
Na sequência, temos um algoritmo e seus fluxograma e código Python para computar a quarta aproximação de , assumindo como aproximação inicial.
-
•
Algoritmo
-
1.
Entre o valor de .
-
2.
Se , faça:
-
(a)
-
(b)
Para , faça:
-
i.
.
-
i.
-
(c)
Imprime o valor de .
-
(a)
-
3.
Senão, faça:
-
(a)
Imprime mensagem “Não existe!”.
-
(a)
-
1.
-
•
Fluxograma
Consulte a Figura 2.2.
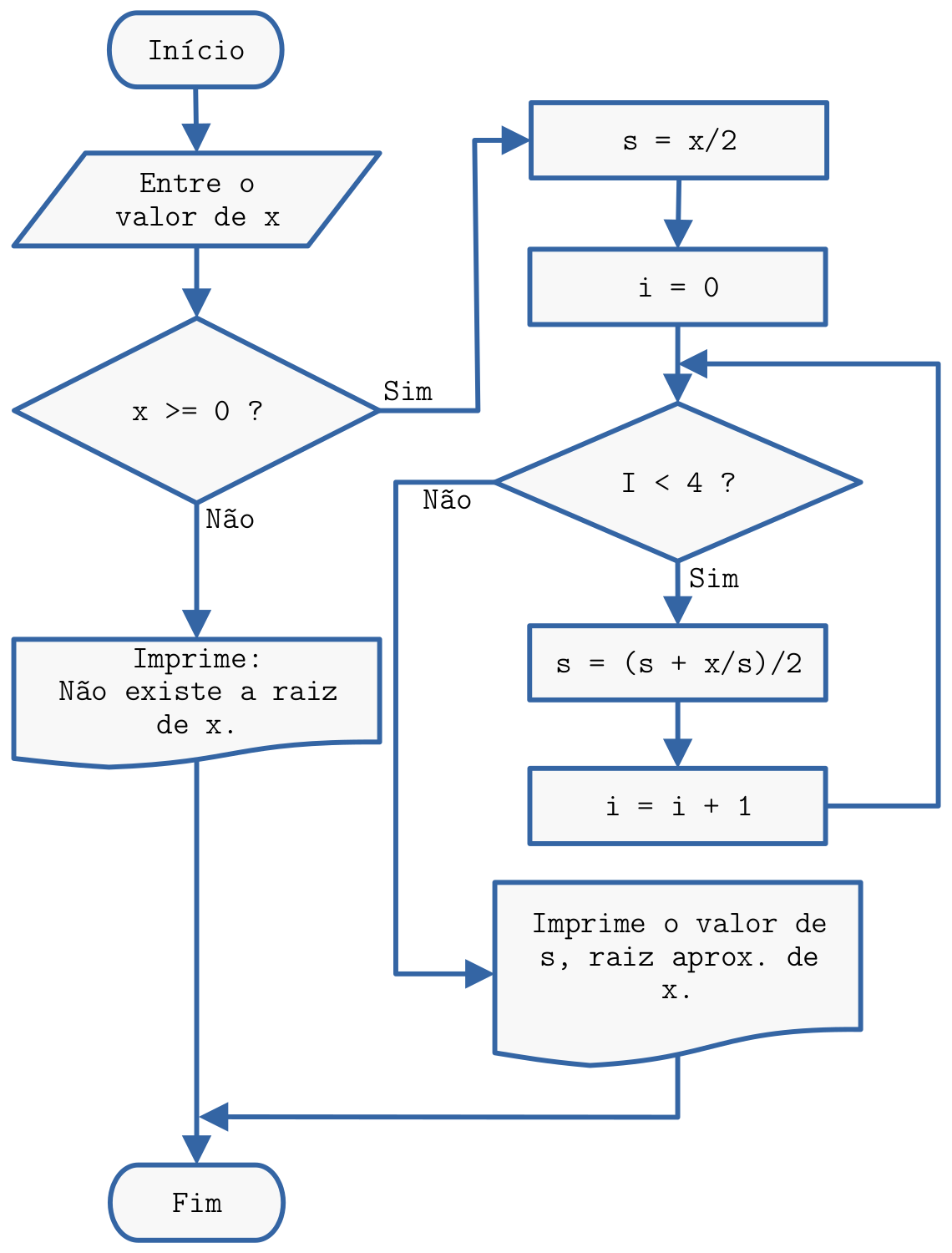
Figura 2.2: Fluxograma referente ao Exemplo 2.2.2. -
•
Código Python
Código 1: metHeron.py 1x = float(input('Entre com o valor de x: '))2if (x >= 0.):3 s = x/24 for i in range(4):5 s = (s + x/s)/26 print(f'Raiz aprox. de x = {s}')7else:8 print(f'Não existe!')
O algoritmo tem um bug (um erro)! Consulte o Exercício E.2.2.11.
Algoritmos escritos em uma forma próxima de uma linguagem computacional são, também, chamados de pseudocódigos. Na prática, pseudocódigos e fluxogramas são usados para apresentar uma forma mais geral e menos detalhada de um algoritmo. Usualmente, sua forma detalhada é escrita diretamente em uma linguagem computacional escolhida.
2.2.2 Exercícios
E. 2.2.1.
Complete as lacunas.
-
a)
Programar é desenvolver um software para ser executado em um computador.
-
b)
Linguagens computacionais tem uma sintaxe simples, precisa e sem ambiguidades.
-
c)
Um algoritmo é uma sequência finita de passos bem definidos que permitem a resolução objetiva de um problema em tempo finito.
-
d)
Pseudocódigo é um algoritmo escrito em uma forma próxima de uma linguagem computacional.
Resposta 0.
a) programa/código/software. b) sintaxe. c) bem definidos; objetiva; finito. d) Pseudocódigo.
E. 2.2.2.
Complete as lacunas.
-
a)
Fluxograma é uma representação gráfica de um algoritmo.
-
b)
Em um fluxograma, terminal indicada o início ou final de um algoritmo.
-
c)
A linha de fluxo direciona para o próximo bloco de execução.
-
d)
A leitura de dados é indicada por um bloco de entrada em um fluxograma.
-
e)
Um bloco de processo indica uma ação a ser executada.
-
f)
Uma ramificação do algoritmo é indicada no seu fluxograma por um bloco de decisão.
-
g)
Em um fluxograma, o bloco de saída indica a impressão de um dado.
Resposta 0.
a) Fluxograma. b) terminal. c) linha de fluxo; execução. d) entrada. e) processo. f) decisão. g) saída.
E. 2.2.3.
Escreva um algoritmo/pseudocódigo e um fluxograma correspondente computar a média aritmética entre dois números e dados. Como desafio, tente escrever um código Python baseado em seu algoritmo.
Resposta 0.
-
•
Algoritmo
1. Entre com os valores de x e y 2. m = (x + y)/2 3. Imprime m
-
•
Fluxograma
![[Uncaptioned image]](cap_lingua/dados/fig_resp_media/fig.png)
E. 2.2.4.
Escreva um algoritmo/pseudocódigo e um fluxograma correspondente para computar a área de um quadrado de lado dado. Como desafio, tente escrever um código Python baseado em seu algoritmo.
Resposta 0.
-
•
Algoritmo
1. Entre com o valor de l 2. area = l*l 3. Imprime area
E. 2.2.5.
Escreva um algoritmo/pseudocódigo e um fluxograma correspondente para computar a área de um retângulo de lados dados. Como desafio, tente escrever um código Python baseado em seu algoritmo.
Resposta 0.
1. Entre com o valor de a 2. Entre com o valor de b 3. area = a*b 4. Imprime area
E. 2.2.6.
Escreva um algoritmo/pseudocódigo e um fluxograma correspondente para computar a área de um triângulo retângulo de dada hipotenusa e um dos lados dado. Como desafio, tente escrever um código Python baseado em seu algoritmo.
Resposta 0.
-
•
Algoritmo
1. Entre com o valor de h 2. Entre com o valor de l # o outro cateto 3. m = sqrt(h*h - l*l) 4. area = m*l/2. 5. Imprime area
-
•
Fluxograma
![[Uncaptioned image]](cap_lingua/dados/fig_resp_triaRet/fig.png)
E. 2.2.7.
Escreva um algoritmo/pseudocódigo e um fluxograma correspondente para computar o zero de uma função afim
| (2.3) |
dados os coeficientes e . Como desafio, tente escrever um código Python baseado em seu algoritmo.
Resposta 0.
1. Entre com o valor de a 2. Entre com o valor de b 3. x0 = -b/a 4. Imprime x0
E. 2.2.8.
Escreva um algoritmo/pseudocódigo e um fluxograma correspondente para computar as raízes reais de um polinômio quadrático
| (2.4) |
dados os coeficientes , e . Como desafio, tente escrever um código Python baseado em seu algoritmo.
Resposta 0.
1. Entre com o valor de a 2. Entre com o valor de b 3. Entre com o valor de c # discriminante 4. delta = b*b - 4.*a*c # raízes 5. x1 = (-b - sqrt(delta))/2. 6. x2 = (-b + sqrt(delta))/2. 7. Imprime x1 e x2
E. 2.2.9.
A Série Harmônica é defina por
| (2.5) |
Escreva um algoritmo/pseudocódigo e um fluxograma corresponde para computar o valor da série harmônica truncada em , com dado. Ou seja, dado , o objetivo é calcular
| (2.6) |
Resposta 0.
-
•
Algoritmo
1. Entre com o valor de n. 2. s = 0. 3. Para i = 1, 2, ... n: 3.1. s = s + 1./i 4. Imprime s
-
•
Fluxograma
![[Uncaptioned image]](cap_lingua/dados/fig_resp_serieHarmonica/fig.png)
E. 2.2.10.
Escreva um algoritmo/pseudocódigo e um fluxograma corresponde para computar o fatorial de um dado número natural , i.e. computar
| (2.7) |
Resposta 0.
1. Entre com o valor de n 2. fat = 1 3. Para i = 2, ..., n: 3.1. fat = fat*i 4. Imprime fat
E. 2.2.11.
Resposta 0.
Dica: o bug ocorre quando .
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.
Algoritmos e Programação I
2.2 Algoritmos e programação
Programar é criar um programa (um software) para ser executado em computador. Para isso, escreve-se um código em uma linguagem computacional (por exemplo, em Python), o qual é interpretado/compilado para gerar o programa final. Linguagens computacionais são técnicas, utilizam uma sintaxe simples, precisa e sem ambiguidades. Ou seja, para criarmos um programa com um determinado objetivo, precisamos escrever um código computacional técnico, que siga a sintaxe da linguagem escolhida e sem ambiguidades.
Um algoritmo pode ser definido uma sequencia ordenada e sem ambiguidade de passos para a resolução de um problema.
Exemplo 2.2.1.
O cálculo da área de um triângulo de base e altura dadas por ser feito com o seguinte algoritmo:
-
1.
Informe o valor da base .
-
2.
Informe o valor da altura .
-
3.
.
-
4.
Imprima o valor de .
Algoritmos para a programação são pensados para serem facilmente transformados em códigos computacionais. Por exemplo, o algoritmo acima pode ser escrito em Python como segue:
Para criar um programa para resolver um dado problema, começamos desenvolvendo um algoritmo para resolvê-lo, este algoritmo é implementado na linguagem computacional escolhida, a qual gera o programa final. Aqui, o passo mais difícil costuma ser o desenvolvimento do algoritmo. Precisamos pensar em como podemos resolver o problema de interesse em uma sequência de passos ordenada e sem ambiguidades para que possamos implementá-los em computador.
Um algoritmo deve ter as seguintes propriedades:
-
•
Cada passo deve estar bem definido, i.e. não pode conter ambiguidades.
-
•
Cada passo deve contribuir de forma efetiva na solução do problema.
-
•
Deve ter número finito de passos que podem ser computados em um tempo finito.
Observação 2.2.1.(Mulher na matemática)
A primeira pessoa a publicar um algoritmo para programação foi Augusta Ada King77endnote: 7Augusta Ada Byron King, Condessa de Lovelace, 1815 - 1852, matemática inglesa. Fonte: Wikipédia: Ada Lovelace.. O algoritmo foi criado para computar os números de Bernoulli88endnote: 8Jacob Bernoulli, 1655-1705, matemático suíço. Fonte: Wikipédia: Jakob Bernoulli..
2.2.1 Fluxograma
Fluxograma é uma representação gráfica de um algoritmo. Entre outras, usam-se as seguintes formas para representar tipos de ações a serem executadas:
-
•
Terminal: início ou final do algoritmo.
![[Uncaptioned image]](cap_lingua/dados/fig_fluxograma/terminal.png)
-
•
Linha de fluxo: direciona para a próxima execução.
![[Uncaptioned image]](cap_lingua/dados/fig_fluxograma/linha.png)
-
•
Entrada: leitura de informação/dados.
![[Uncaptioned image]](cap_lingua/dados/fig_fluxograma/entrada.png)
-
•
Processo: ação a ser executada.
![[Uncaptioned image]](cap_lingua/dados/fig_fluxograma/processo.png)
-
•
Decisão: ramificação do processamento baseada em uma condição.
![[Uncaptioned image]](cap_lingua/dados/fig_fluxograma/decisao.png)
-
•
Saída: impressão de informação/dados.
![[Uncaptioned image]](cap_lingua/dados/fig_fluxograma/saida.png)
Exemplo 2.2.2.
O método de Heron99endnote: 9Heron de Alexandria, 10 - 80, matemático grego. Fonte: Wikipédia: Heron de Alexandria. é um algoritmo para o cálculo aproximado da raiz quadrada de um dado número , i.e. . Consiste na iteração
| (2.1) | |||
| (2.2) |
para , onde é o número de iterações calculadas.
Na sequência, temos um algoritmo e seus fluxograma e código Python para computar a quarta aproximação de , assumindo como aproximação inicial.
-
•
Algoritmo
-
1.
Entre o valor de .
-
2.
Se , faça:
-
(a)
-
(b)
Para , faça:
-
i.
.
-
i.
-
(c)
Imprime o valor de .
-
(a)
-
3.
Senão, faça:
-
(a)
Imprime mensagem “Não existe!”.
-
(a)
-
1.
-
•
Fluxograma
Consulte a Figura 2.2.

Figura 2.2: Fluxograma referente ao Exemplo 2.2.2. -
•
Código Python
Código 1: metHeron.py 1x = float(input('Entre com o valor de x: '))2if (x >= 0.):3 s = x/24 for i in range(4):5 s = (s + x/s)/26 print(f'Raiz aprox. de x = {s}')7else:8 print(f'Não existe!')
O algoritmo tem um bug (um erro)! Consulte o Exercício E.2.2.11.
Algoritmos escritos em uma forma próxima de uma linguagem computacional são, também, chamados de pseudocódigos. Na prática, pseudocódigos e fluxogramas são usados para apresentar uma forma mais geral e menos detalhada de um algoritmo. Usualmente, sua forma detalhada é escrita diretamente em uma linguagem computacional escolhida.
2.2.2 Exercícios
E. 2.2.1.
Complete as lacunas.
-
a)
Programar é desenvolver um software para ser executado em um computador.
-
b)
Linguagens computacionais tem uma sintaxe simples, precisa e sem ambiguidades.
-
c)
Um algoritmo é uma sequência finita de passos bem definidos que permitem a resolução objetiva de um problema em tempo finito.
-
d)
Pseudocódigo é um algoritmo escrito em uma forma próxima de uma linguagem computacional.
Resposta 0.
a) programa/código/software. b) sintaxe. c) bem definidos; objetiva; finito. d) Pseudocódigo.
E. 2.2.2.
Complete as lacunas.
-
a)
Fluxograma é uma representação gráfica de um algoritmo.
-
b)
Em um fluxograma, terminal indicada o início ou final de um algoritmo.
-
c)
A linha de fluxo direciona para o próximo bloco de execução.
-
d)
A leitura de dados é indicada por um bloco de entrada em um fluxograma.
-
e)
Um bloco de processo indica uma ação a ser executada.
-
f)
Uma ramificação do algoritmo é indicada no seu fluxograma por um bloco de decisão.
-
g)
Em um fluxograma, o bloco de saída indica a impressão de um dado.
Resposta 0.
a) Fluxograma. b) terminal. c) linha de fluxo; execução. d) entrada. e) processo. f) decisão. g) saída.
E. 2.2.3.
Escreva um algoritmo/pseudocódigo e um fluxograma correspondente computar a média aritmética entre dois números e dados. Como desafio, tente escrever um código Python baseado em seu algoritmo.
Resposta 0.
-
•
Algoritmo
1. Entre com os valores de x e y 2. m = (x + y)/2 3. Imprime m
-
•
Fluxograma
![[Uncaptioned image]](cap_lingua/dados/fig_resp_media/fig.png)
E. 2.2.4.
Escreva um algoritmo/pseudocódigo e um fluxograma correspondente para computar a área de um quadrado de lado dado. Como desafio, tente escrever um código Python baseado em seu algoritmo.
Resposta 0.
-
•
Algoritmo
1. Entre com o valor de l 2. area = l*l 3. Imprime area
E. 2.2.5.
Escreva um algoritmo/pseudocódigo e um fluxograma correspondente para computar a área de um retângulo de lados dados. Como desafio, tente escrever um código Python baseado em seu algoritmo.
Resposta 0.
1. Entre com o valor de a 2. Entre com o valor de b 3. area = a*b 4. Imprime area
E. 2.2.6.
Escreva um algoritmo/pseudocódigo e um fluxograma correspondente para computar a área de um triângulo retângulo de dada hipotenusa e um dos lados dado. Como desafio, tente escrever um código Python baseado em seu algoritmo.
Resposta 0.
-
•
Algoritmo
1. Entre com o valor de h 2. Entre com o valor de l # o outro cateto 3. m = sqrt(h*h - l*l) 4. area = m*l/2. 5. Imprime area
-
•
Fluxograma
![[Uncaptioned image]](cap_lingua/dados/fig_resp_triaRet/fig.png)
E. 2.2.7.
Escreva um algoritmo/pseudocódigo e um fluxograma correspondente para computar o zero de uma função afim
| (2.3) |
dados os coeficientes e . Como desafio, tente escrever um código Python baseado em seu algoritmo.
Resposta 0.
1. Entre com o valor de a 2. Entre com o valor de b 3. x0 = -b/a 4. Imprime x0
E. 2.2.8.
Escreva um algoritmo/pseudocódigo e um fluxograma correspondente para computar as raízes reais de um polinômio quadrático
| (2.4) |
dados os coeficientes , e . Como desafio, tente escrever um código Python baseado em seu algoritmo.
Resposta 0.
1. Entre com o valor de a 2. Entre com o valor de b 3. Entre com o valor de c # discriminante 4. delta = b*b - 4.*a*c # raízes 5. x1 = (-b - sqrt(delta))/2. 6. x2 = (-b + sqrt(delta))/2. 7. Imprime x1 e x2
E. 2.2.9.
A Série Harmônica é defina por
| (2.5) |
Escreva um algoritmo/pseudocódigo e um fluxograma corresponde para computar o valor da série harmônica truncada em , com dado. Ou seja, dado , o objetivo é calcular
| (2.6) |
Resposta 0.
-
•
Algoritmo
1. Entre com o valor de n. 2. s = 0. 3. Para i = 1, 2, ... n: 3.1. s = s + 1./i 4. Imprime s
-
•
Fluxograma
![[Uncaptioned image]](cap_lingua/dados/fig_resp_serieHarmonica/fig.png)
E. 2.2.10.
Escreva um algoritmo/pseudocódigo e um fluxograma corresponde para computar o fatorial de um dado número natural , i.e. computar
| (2.7) |
Resposta 0.
1. Entre com o valor de n 2. fat = 1 3. Para i = 2, ..., n: 3.1. fat = fat*i 4. Imprime fat
E. 2.2.11.
Resposta 0.
Dica: o bug ocorre quando .
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.